1. 单向链表的基础操作
1.1 数据结构定义
c
// 单向链表节点结构
typedef struct ListNode {
int val;
struct ListNode* next;
} ListNode;1.2 单向链表的销毁
链表的销毁是内存管理的关键环节,必须确保每个节点都被正确释放。
c
/**
* 销毁单向链表
* @param head 链表头指针的地址(二级指针)
* @return 无
*/
void destroyLinkedList(ListNode** head) {
if (head == NULL || *head == NULL) {
return;
}
ListNode* current = *head;
ListNode* next = NULL;
// 遍历链表,逐个释放节点
while (current != NULL) {
next = current->next; // 保存下一个节点
free(current); // 释放当前节点
current = next; // 移动到下一个节点
}
*head = NULL; // 重要:将头指针置为NULL,防止野指针
}
// 使用示例
void testDestroy() {
ListNode* head = createNode(1);
head->next = createNode(2);
head->next->next = createNode(3);
printf("销毁前链表长度: %d\n", getLength(head));
destroyLinkedList(&head);
if (head == NULL) {
printf("链表已成功销毁\n");
}
}2. 单向链表的关键算法
2.1 查找中间节点
查找链表的中间节点是面试中的常见问题,使用快慢指针法可以高效解决。
c
/**
* 查找链表的中间节点
* @param head 链表头指针
* @return 中间节点的指针
*
* 算法思想:快慢指针法
* - 慢指针每次走1步,快指针每次走2步
* - 当快指针到达链表末尾时,慢指针正好在中间
* - 时间复杂度:O(n),空间复杂度:O(1)
*/
ListNode* findMiddleNode(ListNode* head) {
if (head == NULL || head->next == NULL) {
return head;
}
ListNode* slow = head; // 慢指针
ListNode* fast = head; // 快指针
while (fast != NULL && fast->next != NULL) {
slow = slow->next; // 慢指针走一步
fast = fast->next->next; // 快指针走两步
}
return slow;
}
// 测试中间节点查找
void testFindMiddle() {
// 创建链表: 1->2->3->4->5
ListNode* head = createListFromArray(1, 2, 3, 4, 5);
ListNode* middle = findMiddleNode(head);
printf("中间节点值: %d\n", middle->val); // 输出: 3
// 偶数个节点的测试: 1->2->3->4
ListNode* head2 = createListFromArray(1, 2, 3, 4);
ListNode* middle2 = findMiddleNode(head2);
printf("中间节点值: %d\n", middle2->val); // 输出: 3
}2.2 查找倒数第k个节点
查找倒数第k个节点也是链表操作中的经典问题。
c
/**
* 查找倒数第k个节点
* @param head 链表头指针
* @param k 倒数第k个
* @return 倒数第k个节点的指针
*
* 算法思想:双指针法
* 1. 先让快指针走k步
* 2. 然后快慢指针一起走
* 3. 当快指针到达末尾时,慢指针就是倒数第k个节点
*/
ListNode* findKthFromEnd(ListNode* head, int k) {
if (head == NULL || k <= 0) {
return NULL;
}
ListNode* fast = head;
ListNode* slow = head;
// 快指针先走k步
for (int i = 0; i < k; i++) {
if (fast == NULL) {
// k大于链表长度
return NULL;
}
fast = fast->next;
}
// 快慢指针一起走
while (fast != NULL) {
slow = slow->next;
fast = fast->next;
}
return slow;
}
// 测试倒数第k个节点查找
void testFindKthFromEnd() {
ListNode* head = createListFromArray(1, 2, 3, 4, 5);
// 测试倒数第1个节点
ListNode* node1 = findKthFromEnd(head, 1);
printf("倒数第1个节点: %d\n", node1->val); // 输出: 5
// 测试倒数第3个节点
ListNode* node3 = findKthFromEnd(head, 3);
printf("倒数第3个节点: %d\n", node3->val); // 输出: 3
// 测试边界情况
ListNode* node5 = findKthFromEnd(head, 5);
printf("倒数第5个节点: %d\n", node5->val); // 输出: 1
}2.3 链表倒置
链表倒置是链表操作中必须掌握的基本功。
c
/**
* 倒置单向链表
* @param head 链表头指针
* @return 倒置后的链表头指针
*
* 算法思想:迭代法
* 1. 维护三个指针:prev, current, next
* 2. 逐个反转节点的next指针
* 3. 时间复杂度:O(n),空间复杂度:O(1)
*/
ListNode* reverseList(ListNode* head) {
ListNode* prev = NULL; // 前驱节点
ListNode* current = head; // 当前节点
ListNode* next = NULL; // 后继节点
while (current != NULL) {
// 保存下一个节点
next = current->next;
// 反转当前节点的指针
current->next = prev;
// 移动指针
prev = current;
current = next;
}
return prev; // prev成为新的头节点
}
// 递归实现链表倒置
ListNode* reverseListRecursive(ListNode* head) {
// 递归终止条件:空链表或只有一个节点
if (head == NULL || head->next == NULL) {
return head;
}
// 递归反转后续链表
ListNode* newHead = reverseListRecursive(head->next);
// 反转当前节点
head->next->next = head;
head->next = NULL;
return newHead;
}
// 测试链表倒置
void testReverseList() {
ListNode* head = createListFromArray(1, 2, 3, 4, 5);
printf("原始链表: ");
printList(head);
ListNode* reversed = reverseList(head);
printf("倒置后链表: ");
printList(reversed);
// 再次倒置(恢复原状)
ListNode* restored = reverseList(reversed);
printf("再次倒置后: ");
printList(restored);
}2.4 链表排序
链表排序相比数组排序更为复杂,这里介绍归并排序的实现。
c
/**
* 对链表进行归并排序
* @param head 链表头指针
* @return 排序后的链表头指针
*
* 算法思想:归并排序(递归)
* 1. 找到链表中点,将链表分为两半
* 2. 递归对两半进行排序
* 3. 合并两个已排序的链表
* 4. 时间复杂度:O(n log n),空间复杂度:O(log n)(递归栈)
*/
ListNode* sortList(ListNode* head) {
// 递归终止条件
if (head == NULL || head->next == NULL) {
return head;
}
// 找到链表中点(快慢指针法)
ListNode* slow = head;
ListNode* fast = head;
ListNode* prev = NULL; // 记录中点的前一个节点
while (fast != NULL && fast->next != NULL) {
prev = slow;
slow = slow->next;
fast = fast->next->next;
}
// 分割链表
if (prev != NULL) {
prev->next = NULL;
}
// 递归排序两半
ListNode* left = sortList(head);
ListNode* right = sortList(slow);
// 合并两个已排序的链表
return mergeSortedLists(left, right);
}
/**
* 合并两个已排序的链表
*/
ListNode* mergeSortedLists(ListNode* l1, ListNode* l2) {
// 创建哑节点简化操作
ListNode dummy;
ListNode* tail = &dummy;
// 比较两个链表的节点,选择较小的加入新链表
while (l1 != NULL && l2 != NULL) {
if (l1->val <= l2->val) {
tail->next = l1;
l1 = l1->next;
} else {
tail->next = l2;
l2 = l2->next;
}
tail = tail->next;
}
// 将剩余部分连接到新链表
if (l1 != NULL) {
tail->next = l1;
} else {
tail->next = l2;
}
return dummy.next;
}
// 测试链表排序
void testSortList() {
// 创建乱序链表: 5->2->8->1->9->3
ListNode* head = createListFromArray(5, 2, 8, 1, 9, 3);
printf("排序前: ");
printList(head);
ListNode* sorted = sortList(head);
printf("排序后: ");
printList(sorted);
}3. 单向链表的环检测与处理
3.1 判断链表是否有环
使用快慢指针法(Floyd判圈算法)可以高效检测链表是否有环。
c
/**
* 判断链表是否有环
* @param head 链表头指针
* @return 如果有环返回相遇点,否则返回NULL
*
* 算法思想:快慢指针法(Floyd判圈算法)
* - 快指针每次走2步,慢指针每次走1步
* - 如果有环,快慢指针一定会相遇
* - 时间复杂度:O(n),空间复杂度:O(1)
*/
ListNode* hasCycle(ListNode* head) {
if (head == NULL || head->next == NULL) {
return NULL;
}
ListNode* slow = head; // 慢指针,每次走1步
ListNode* fast = head; // 快指针,每次走2步
while (fast != NULL && fast->next != NULL) {
slow = slow->next; // 慢指针走一步
fast = fast->next->next; // 快指针走两步
// 如果相遇,说明有环
if (slow == fast) {
return slow; // 返回相遇点
}
}
// 快指针到达链表末尾,说明无环
return NULL;
}
// 测试环检测
void testCycleDetection() {
// 创建无环链表
ListNode* list1 = createListFromArray(1, 2, 3, 4, 5);
printf("链表1是否有环: %s\n",
hasCycle(list1) ? "有环" : "无环");
// 创建有环链表: 1->2->3->4->5->3(形成环)
ListNode* list2 = createListFromArray(1, 2, 3, 4, 5);
// 找到节点3
ListNode* node3 = list2->next->next;
// 找到尾节点并连接到节点3
ListNode* tail = list2;
while (tail->next != NULL) {
tail = tail->next;
}
tail->next = node3; // 形成环
printf("链表2是否有环: %s\n",
hasCycle(list2) ? "有环" : "无环");
// 注意:有环链表不能直接销毁,需要先断开环
tail->next = NULL;
destroyLinkedList(&list2);
}3.2 获取环的长度
一旦检测到环,我们可以计算环的长度。
c
/**
* 获取环的长度
* @param meetingPoint 快慢指针相遇点
* @return 环的长度
*
* 算法思想:
* 1. 从相遇点出发,走一圈回到相遇点
* 2. 统计步数即为环长
*/
int getCycleLength(ListNode* meetingPoint) {
if (meetingPoint == NULL) {
return 0;
}
ListNode* current = meetingPoint->next;
int length = 1; // 从1开始,因为meetingPoint已经在环上
while (current != meetingPoint) {
current = current->next;
length++;
}
return length;
}
// 测试获取环长
void testGetCycleLength() {
// 创建有环链表: 1->2->3->4->5->3
ListNode* head = createListFromArray(1, 2, 3, 4, 5);
ListNode* node3 = head->next->next;
ListNode* tail = head;
while (tail->next != NULL) {
tail = tail->next;
}
tail->next = node3;
// 检测环并获取相遇点
ListNode* meetingPoint = hasCycle(head);
if (meetingPoint != NULL) {
int cycleLength = getCycleLength(meetingPoint);
printf("环的长度为: %d\n", cycleLength); // 输出: 3
}
// 断开环并销毁链表
tail->next = NULL;
destroyLinkedList(&head);
}3.3 获取环的入口位置
找到环的入口是环检测问题的关键。
c
/**
* 获取环的入口位置
* @param head 链表头指针
* @return 环的入口节点指针
*
* 算法思想:
* 1. 先用快慢指针找到相遇点
* 2. 将一个指针重置到头节点,两个指针每次都走一步
* 3. 再次相遇的位置就是环入口
*
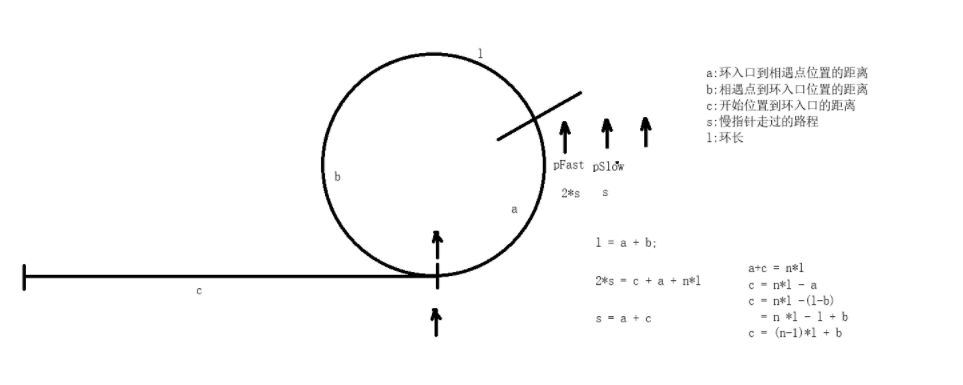
* 数学原理:
* 设头节点到环入口距离为a,环入口到相遇点距离为b,相遇点到环入口距离为c
* 快指针走的距离:a + n(b+c) + b
* 慢指针走的距离:a + b
* 由于快指针速度是慢指针的2倍:2(a+b) = a + n(b+c) + b
* 化简得:a = c + (n-1)(b+c)
* 这意味着从头节点走到环入口的距离等于从相遇点走到环入口的距离
*/
ListNode* detectCycleEntry(ListNode* head) {
// 步骤1:检测是否有环并找到相遇点
ListNode* meetingPoint = hasCycle(head);
if (meetingPoint == NULL) {
return NULL; // 无环
}
// 步骤2:找到环入口
ListNode* ptr1 = head; // 从链表头开始
ListNode* ptr2 = meetingPoint; // 从相遇点开始
while (ptr1 != ptr2) {
ptr1 = ptr1->next; // 每次走一步
ptr2 = ptr2->next; // 每次走一步
}
return ptr1; // 相遇点即为环入口
}
// 测试获取环入口
void testDetectCycleEntry() {
// 创建有环链表: 1->2->3->4->5->3
ListNode* head = createListFromArray(1, 2, 3, 4, 5);
ListNode* node3 = head->next->next; // 环入口
ListNode* tail = head;
while (tail->next != NULL) {
tail = tail->next;
}
tail->next = node3; // 形成环
ListNode* entry = detectCycleEntry(head);
if (entry != NULL) {
printf("环入口节点的值为: %d\n", entry->val); // 输出: 3
}
// 断开环并销毁链表
tail->next = NULL;
destroyLinkedList(&head);
}4. 双向链表的实现
双向链表相比单向链表,每个节点多了一个指向前驱节点的指针,这使得双向链表在插入、删除操作上更加高效。
4.1 数据结构定义
c
// 双向链表节点结构
typedef struct DListNode {
int val;
struct DListNode* prev; // 前驱指针
struct DListNode* next; // 后继指针
} DListNode;4.2 双向链表的创建和销毁
c
/**
* 创建双向链表节点
* @param val 节点值
* @return 新创建的节点指针
*/
DListNode* createDListNode(int val) {
DListNode* node = (DListNode*)malloc(sizeof(DListNode));
if (node == NULL) {
printf("内存分配失败\n");
return NULL;
}
node->val = val;
node->prev = NULL;
node->next = NULL;
return node;
}
/**
* 销毁双向链表
* @param head 链表头指针的地址
*
* 注意:与单向链表销毁类似,但需要处理prev指针
*/
void destroyDLinkedList(DListNode** head) {
if (head == NULL || *head == NULL) {
return;
}
DListNode* current = *head;
DListNode* next = NULL;
while (current != NULL) {
next = current->next;
free(current);
current = next;
}
*head = NULL;
printf("双向链表已销毁\n");
}
// 创建双向链表示例
DListNode* createDListFromArray(int* arr, int size) {
if (arr == NULL || size <= 0) {
return NULL;
}
DListNode* head = createDListNode(arr[0]);
DListNode* tail = head;
for (int i = 1; i < size; i++) {
DListNode* newNode = createDListNode(arr[i]);
tail->next = newNode;
newNode->prev = tail;
tail = newNode;
}
return head;
}4.3 双向链表的头插和尾插
c
/**
* 双向链表头插法
* @param head 链表头指针的地址
* @param val 要插入的值
*/
void insertAtHead(DListNode** head, int val) {
DListNode* newNode = createDListNode(val);
if (*head == NULL) {
*head = newNode;
return;
}
// 新节点成为头节点
newNode->next = *head;
(*head)->prev = newNode;
*head = newNode;
}
/**
* 双向链表尾插法
* @param head 链表头指针的地址
* @param val 要插入的值
*/
void insertAtTail(DListNode** head, int val) {
DListNode* newNode = createDListNode(val);
if (*head == NULL) {
*head = newNode;
return;
}
// 找到尾节点
DListNode* tail = *head;
while (tail->next != NULL) {
tail = tail->next;
}
// 在尾节点后插入新节点
tail->next = newNode;
newNode->prev = tail;
}
// 测试头插和尾插
void testInsertOperations() {
DListNode* head = NULL;
// 尾插法构建链表: 1->2->3
insertAtTail(&head, 1);
insertAtTail(&head, 2);
insertAtTail(&head, 3);
printf("尾插后链表: ");
printDListForward(head); // 输出: 1->2->3
// 头插法插入0
insertAtHead(&head, 0);
printf("头插0后链表: ");
printDListForward(head); // 输出: 0->1->2->3
}4.4 双向链表的遍历
双向链表支持正向和反向两种遍历方式。
c
/**
* 正向遍历双向链表
* @param head 链表头指针
*/
void printDListForward(DListNode* head) {
DListNode* current = head;
printf("正向遍历: ");
while (current != NULL) {
printf("%d", current->val);
if (current->next != NULL) {
printf(" <-> ");
}
current = current->next;
}
printf(" -> NULL\n");
}
/**
* 反向遍历双向链表
* @param head 链表头指针
*/
void printDListBackward(DListNode* head) {
if (head == NULL) {
printf("链表为空\n");
return;
}
// 先找到尾节点
DListNode* tail = head;
while (tail->next != NULL) {
tail = tail->next;
}
printf("反向遍历: NULL");
// 从尾节点开始向前遍历
while (tail != NULL) {
printf(" <- %d", tail->val);
tail = tail->prev;
}
printf("\n");
}
// 测试双向链表遍历
void testDListTraversal() {
int arr[] = {1, 2, 3, 4, 5};
DListNode* head = createDListFromArray(arr, 5);
printDListForward(head); // 输出: 1 <-> 2 <-> 3 <-> 4 <-> 5 -> NULL
printDListBackward(head); // 输出: NULL <- 5 <- 4 <- 3 <- 2 <- 1
destroyDLinkedList(&head);
}4.5 双向链表的删除操作
双向链表的删除操作比单向链表更高效,因为可以直接通过前驱指针找到前一个节点。
c
/**
* 删除双向链表中指定值的节点
* @param head 链表头指针的地址
* @param val 要删除的值
* @return 是否成功删除
*/
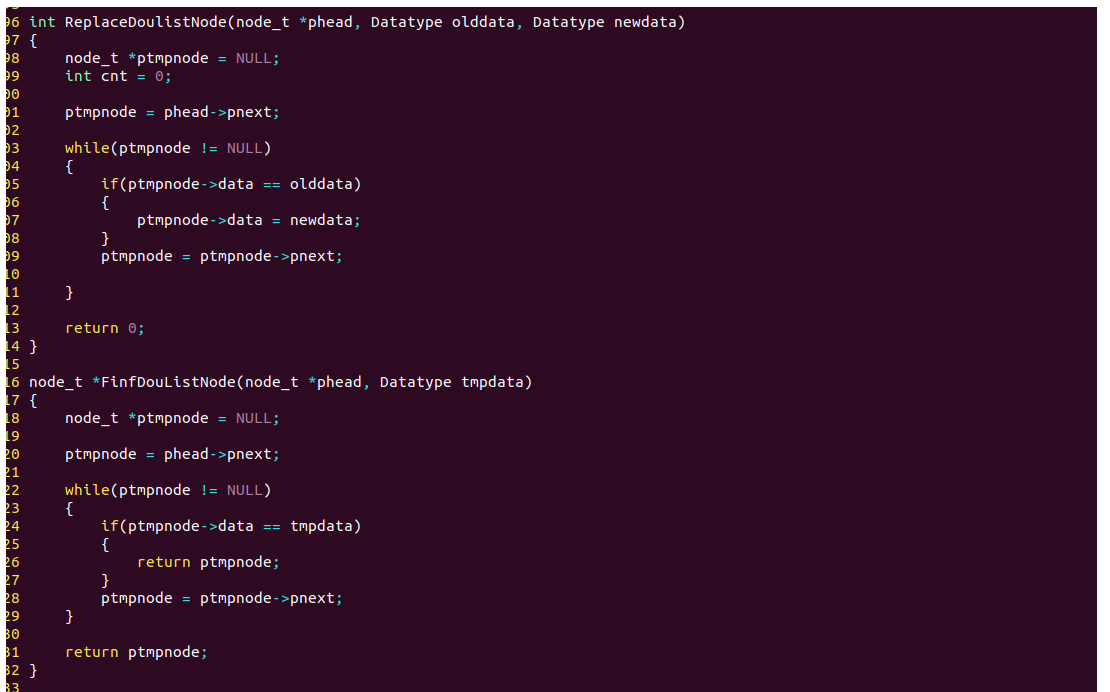
int deleteNode(DListNode** head, int val) {
if (*head == NULL) {
return 0;
}
DListNode* current = *head;
// 遍历查找要删除的节点
while (current != NULL) {
if (current->val == val) {
// 找到要删除的节点
// 调整前驱节点的next指针
if (current->prev != NULL) {
current->prev->next = current->next;
} else {
// 要删除的是头节点
*head = current->next;
}
// 调整后继节点的prev指针
if (current->next != NULL) {
current->next->prev = current->prev;
}
free(current);
return 1; // 删除成功
}
current = current->next;
}
return 0; // 未找到要删除的节点
}
/**
* 删除双向链表中的指定位置节点
* @param head 链表头指针的地址
* @param position 要删除的位置(从0开始)
* @return 是否成功删除
*/
int deleteNodeAtPosition(DListNode** head, int position) {
if (*head == NULL || position < 0) {
return 0;
}
DListNode* current = *head;
int index = 0;
// 遍历到指定位置
while (current != NULL && index < position) {
current = current->next;
index++;
}
// 如果position超出链表长度
if (current == NULL) {
return 0;
}
// 删除节点
if (current->prev != NULL) {
current->prev->next = current->next;
} else {
*head = current->next;
}
if (current->next != NULL) {
current->next->prev = current->prev;
}
free(current);
return 1;
}
// 测试删除操作
void testDeleteOperations() {
int arr[] = {1, 2, 3, 4, 5};
DListNode* head = createDListFromArray(arr, 5);
printf("原始链表: ");
printDListForward(head);
// 删除值为3的节点
deleteNode(&head, 3);
printf("删除3后: ");
printDListForward(head); // 输出: 1 <-> 2 <-> 4 <-> 5
// 删除位置1的节点(值为2)
deleteNodeAtPosition(&head, 1);
printf("删除位置1后: ");
printDListForward(head); // 输出: 1 <-> 4 <-> 5
destroyDLinkedList(&head);
}4.6双向链表的查找与替换
5. 链表操作的时间复杂度对比
| 操作 | 单向链表 | 双向链表 | 备注 |
|---|---|---|---|
| 访问节点 | O(n) | O(n) | 都需要遍历 |
| 插入头节点 | O(1) | O(1) | 两者都高效 |
| 插入尾节点 | O(n) | O(1) | 双向链表维护尾指针时更优 |
| 删除指定节点 | O(n) | O(1) | 双向链表直接定位更高效 |
| 查找中间节点 | O(n) | O(n) | 都需要快慢指针法 |
| 倒置链表 | O(n) | O(n) | 时间复杂度相同 |
| 判断是否有环 | O(n) | O(n) | 都需要快慢指针法 |
6. 实用技巧和最佳实践
6.1 内存管理注意事项
-
每次malloc后检查返回值:确保内存分配成功
-
每个malloc必须有对应的free:防止内存泄漏
-
free后立即将指针置为NULL:防止野指针
-
有环链表需要先断开环再销毁:避免无限循环
6.2 调试技巧
-
打印链表内容:在关键步骤打印链表状态
-
使用断言:检查链表指针的有效性
-
内存检测工具:使用valgrind等工具检测内存问题
7. 总结
本文详细介绍了链表数据结构的关键操作:
-
单向链表:包括创建、销毁、查找中间节点、查找倒数第k个节点、倒置、排序等基本操作
-
环检测与处理:使用快慢指针法检测环、计算环长、找到环入口
-
双向链表:完整的创建、销毁、插入、遍历、删除操作实现
链表作为基础数据结构,在算法面试和实际开发中都有广泛应用。掌握这些核心操作不仅有助于解决算法问题,也能提高对内存管理和指针操作的理解。