The second week
追光的人永远光芒万丈
一.前言
寒假集训第二周,状态明显比第一周好了很多,一切正常,题单在做,cf在打,现在cf分数1499,希望寒假后能到1600+。
这周补了:归并排序,二分答案,最短路,DAG,容斥定理。
二.部分题解与思路
1.Problem - C - Codeforces
题目复现
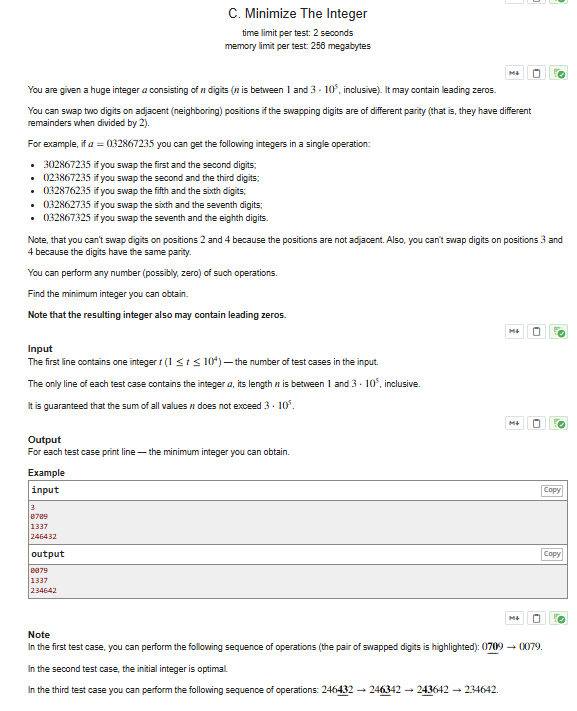
解题思路
归并排序思想,可以 把奇数放到一个序列里,把偶数放到一个序列里,然后用类似归并的方法由小到大归并进一个序列这个序列就是答案,注意最后加末尾标记方便归并。
code
cpp
#include<bits/stdc++.h>
using namespace std;
using ll=long long ;
const int N=2e6+5;
int suma,sumb;
int main(){
int t;
cin>>t;
while(t--){
string s;
cin>>s;
suma=sumb=0;
string sa,sb;
int len=s.length();
for(int i=0;i<len;i++){
if((s[i]-'1')&1){
sa+=s[i];
suma++;
}
else {
sb+=s[i];
sumb++;
}
}
sa+=120;
sb+=120;
for(int i=0,j=0;i<=suma&&j<=sumb;){
if(sa[i]<sb[j]){
if(sa[i]>='0'&&sa[i]<='9')
cout<<sa[i];
i++;
}
else{
if(sb[j]>='0'&&sb[j]<='9')
cout<<sb[j];
j++;
}
}
cout<<endl;
}
return 0;
}2.Problem - D - Codeforces
题目复现
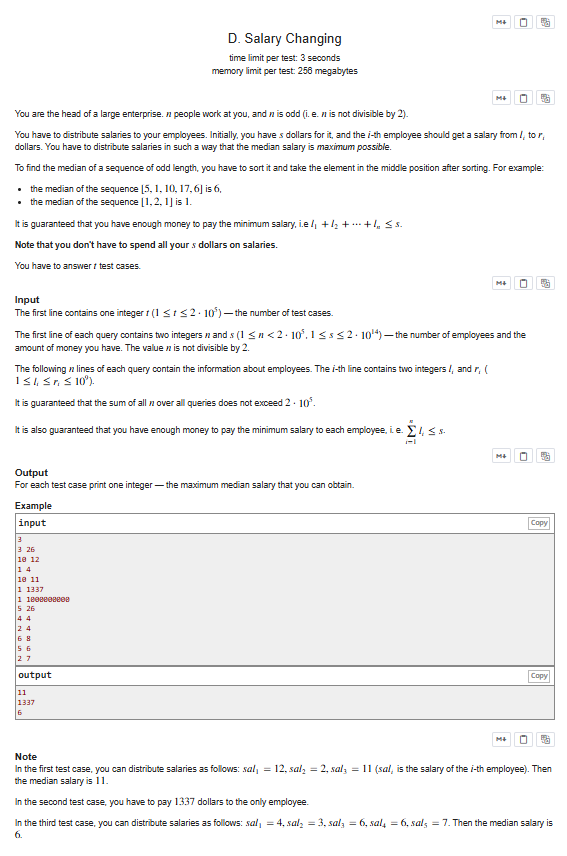
解题思路
二分答案+贪心
二分中位数,贪心判断。问题主要是如何贪心判断是否满足。
我们把第i个员工的薪水范围表示为num[i].l,num[i].r,把当前中位数表示为mid。我们可以把员工的薪水分为三类:
第一类:薪水上界小于中位数,即num[i].r<mid
第二类:薪水下界大于中位数,即num[i].l>mid
第三类:薪水下界小于等于中位数,上界大于等于中位数,即num[i].l<=mid且num[i].r>=mid
对于第一类,薪水一定小于中位数,为了节省钱,我们支付num[i].l的薪水
对于第一类,薪水一定大于中位数,为了节省钱,我们支付num[i].l的薪水
然后我们通过第三类来调节大于等于中位数的薪水数和小于中位数的薪水数,让大于等于中位数的薪水数>小于中位数的薪水数
于是,对于第三类,我们还需支付薪水小于中位数的数量和支付薪水大于中位数的数量是确定的,所以为了节省钱,我们对于下界小的一部分,支付下界num[i].l,对于其他部分,支付中位数mid。
code
cpp
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2e5 + 5;
struct node {
int l, r;
};
struct cmp {
inline bool operator () (const node& a, const node& b) {
return a.l < b.l;
}
};
int T, n, tot[N];
ll s;
inline int check(ll mid) {
int cnt = 0, cnt1 = 0, cnt2 = 0; // cnt为第三类薪水数,cnt1为第一类薪水数,cnt2为第二类薪水数
ll sum = 0;
for(int i = 1; i <= n; ++i) {
if(num[i].r < mid) {
sum += num[i].l;
++cnt1; // 第一类
} else if(num[i].l > mid) {
sum += num[i].l;
++cnt2; // 第二类
} else {
tot[++cnt] = i; // 第三类薪水编号记录
}
}
// 如果第一类或第二类薪水数大于所有薪水数的一半,肯定不满足
if(cnt1 > (n >> 1) || cnt2 > (n >> 1)) return 0;
// 对于num[i].l小的部分
for(int i = 1; i <= (n >> 1) - cnt1; ++i) sum += num[tot[i]].l;
// 其他部分
sum += 1LL * mid * ((n >> 1) + 1 - cnt2);
return sum <= s;
}
node num[N]; // 将数组声明移到全局,避免栈溢出
int main() {
cin >> T;
while(T--) {
cin >> n >> s;
for(int i = 1; i <= n; ++i) {
cin >> num[i].l >> num[i].r;
}
sort(num + 1, num + n + 1, cmp()); // 将num[i].l从小到大排序
ll l = num[(n >> 1) + 1].l, r = 1LL * s / ((n >> 1) + 1); // 二分上下界
while(l <= r) {
ll mid = l + r >> 1;
if(check(mid)) l = mid + 1;
else r = mid - 1;
}
cout << l - 1 << endl;
}
return 0;
}3.Problem - D - Codeforces
题目复现
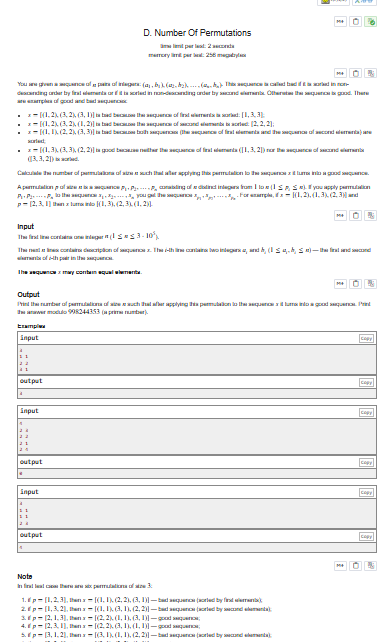
解题思路
任意交换二元组,使得n个二元组不存在一维单调不减。
简单的转换:答案=总方案-单调不减的方案数
由于有两维,容斥,单调不减=第一维单调不减+第二维单调不减-两维都单调不减
单调不减可以排序然后O(n)求出方案数
code
cpp
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int mod = 998244353;
const int N = 1e6 + 5;
int n, ans1, ans2, ans3;
ll jc[N];
struct node {
int x, y;
};
bool cmp(node a, node b) {
if(a.x == b.x) return a.y < b.y;
return a.x < b.x;
}
bool cmp2(node a, node b) {
return a.y < b.y;
}
node a[N];
int main() {
cin >> n;
// 预处理阶乘
jc[0] = 1;
for(int i = 1; i <= n; i++) {
jc[i] = jc[i-1] * i % mod;
}
// 读取点的坐标
for(int i = 1; i <= n; i++) {
cin >> a[i].x >> a[i].y;
}
// 按x排序,计算ans1(x相同的点的排列数乘积)
sort(a + 1, a + n + 1, cmp);
ans1 = 1;
for(int l = 1, r = 1; l <= n; l = r + 1) {
r = l;
while(r < n && a[r+1].x == a[r].x) r++;
int x = r - l + 1;
ans1 = ans1 * jc[x] % mod;
}
// 按y排序,计算ans2(y相同的点的排列数乘积)
sort(a + 1, a + n + 1, cmp2);
ans2 = 1;
for(int l = 1, r = 1; l <= n; l = r + 1) {
r = l;
while(r < n && a[r+1].y == a[r].y) r++;
int x = r - l + 1;
ans2 = ans2 * jc[x] % mod;
}
// 检查是否满足x递增时y也递增,计算ans3
sort(a + 1, a + n + 1, cmp);
bool flag = false;
for(int i = 2; i <= n; i++) {
if(a[i].y < a[i-1].y) {
ans3 = 0;
flag = true;
break; // 找到不满足的情况,直接退出循环
}
}
if(!flag) {
ans3 = 1;
for(int l = 1, r = 1; l <= n; l = r + 1) {
r = l;
while(r < n && a[r+1].x == a[r].x && a[r+1].y == a[r].y) r++;
int x = r - l + 1;
ans3 = ans3 * jc[x] % mod;
}
}
// 计算最终答案,保证结果非负
ll x = ((ans1 + ans2 - ans3) % mod + mod) % mod;
x = (jc[n] - x + mod) % mod;
cout << x << endl;
return 0;
}4.Problem - F - Codeforces
题目复现
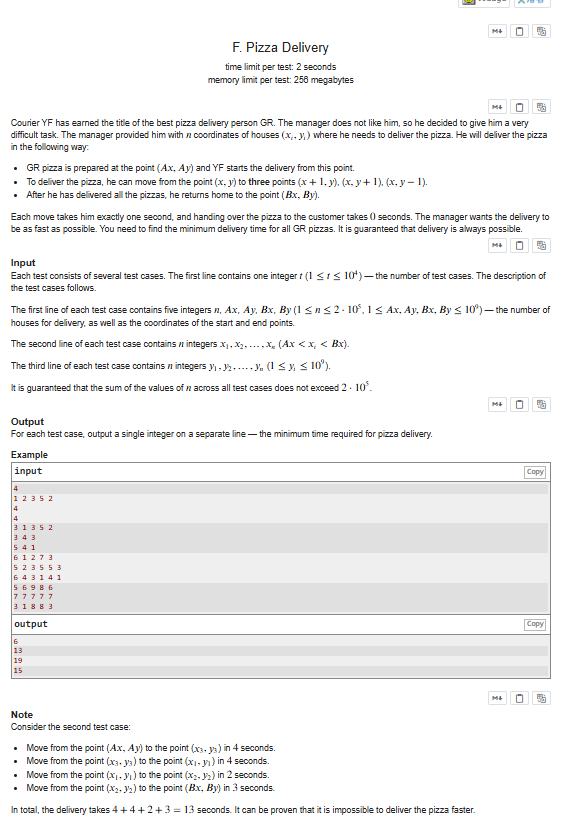
解题思路
首先将所有配送点按横坐标分组,对每个横坐标位置记录该位置所有配送点的纵坐标最小值和最大值(形成 "站点"),并按横坐标升序排序;然后使用DP来计算遍历所有站点的最小纵向移动成本,其中dp0和dp1分别表示到达当前站点纵坐标最小值、最大值时的累计最小成本,通过cost0/cost1函数计算从上个站点到当前站点的纵向移动代价(涵盖从起点 / 上个站点端点到当前站点两端的最优路径);最后将横向必须移动的固定距离(Bx - Ax)与 DP 得到的最小纵向移动成本、以及从最后一个站点到终点 By 的纵向成本相加,得到总最小耗时
code
cpp
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll INF = 1e18;
struct Station {
ll x, mn, mx;
};
ll cost0(ll s, ll a, ll b) {
ll d = b - a;
return min(2*d + abs(s - a), d + abs(s - b));
}
ll cost1(ll s, ll a, ll b) {
ll d = b - a;
return min(d + abs(s - a), 2*d + abs(s - b));
}
void solve() {
ll n, Ax, Ay, Bx, By;
cin >> n >> Ax >> Ay >> Bx >> By;
vector<ll> xs(n), ys(n);
for (int i = 0; i < n; i++) cin >> xs[i];
for (int i = 0; i < n; i++) cin >> ys[i];
if (n == 0) {
cout << (Bx - Ax) + abs(Ay - By) << "\n";
return;
}
map<ll, pair<ll, ll>> mp;
for (int i = 0; i < n; i++) {
ll x = xs[i], y = ys[i];
if (!mp.count(x)) mp[x] = {y, y};
else {
mp[x].first = min(mp[x].first, y);
mp[x].second = max(mp[x].second, y);
}
}
vector<Station> stations;
for (auto &p : mp) {
stations.push_back({p.first, p.second.first, p.second.second});
}
sort(stations.begin(), stations.end(), [](const Station &a, const Station &b) {
return a.x < b.x;
});
int k = stations.size();
ll dp0, dp1;
// initial station (i=0)
{
ll a = stations[0].mn, b = stations[0].mx;
vector<ll> cand = {Ay, a, b};
dp0 = dp1 = INF;
for (ll s : cand) {
dp0 = min(dp0, abs(Ay - s) + cost0(s, a, b));
dp1 = min(dp1, abs(Ay - s) + cost1(s, a, b));
}
}
for (int i = 1; i < k; i++) {
ll a = stations[i].mn, b = stations[i].mx;
ll pa = stations[i-1].mn, pb = stations[i-1].mx;
ll new_dp0 = min(dp0 + cost0(pa, a, b), dp1 + cost0(pb, a, b));
ll new_dp1 = min(dp0 + cost1(pa, a, b), dp1 + cost1(pb, a, b));
dp0 = new_dp0;
dp1 = new_dp1;
}
ll last_a = stations.back().mn, last_b = stations.back().mx;
ll vert = min(dp0 + abs(last_a - By), dp1 + abs(last_b - By));
ll ans = (Bx - Ax) + vert;
cout << ans << "\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
}5.Problem - B - Codeforces
题目复现
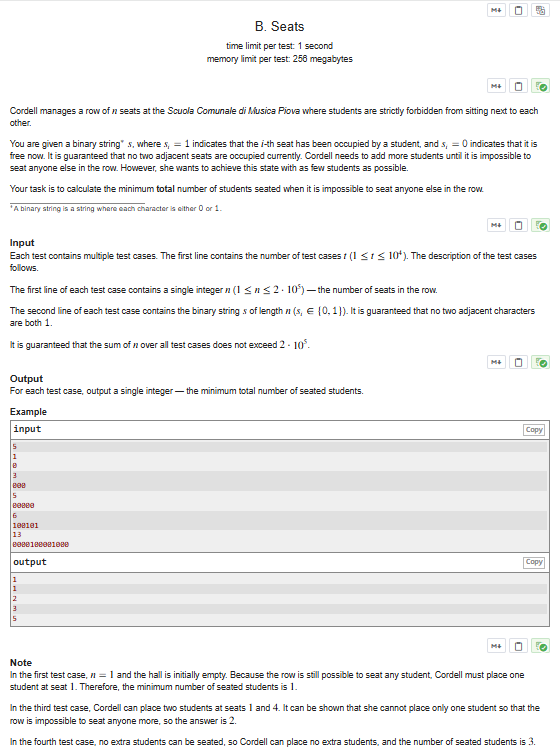
解题思路
每三个连续的空位置能放一个人,分三段嘛,开头到第一个1,两个1中间,最后一个1到结尾,全0是(n+2)/3,中间是算出来长度除3,前后是长度加1除3
code
cpp
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--){
int n;
cin>>n;
string s;
cin>>s;
int init = count(s.begin(), s.end(), '1');
if(init == 0){
cout<<(n+2)/3<<'\n';
continue;
}
int first = -1, last = -1;
for(int i=0; i<n; ++i){
if(s[i]=='1'){
if(first==-1) first=i;
last=i;
}
}
ll add = 0;
if(first > 0){
int l = first;
add += (l+1)/3;
}
if(last < n-1){
int l = n-1-last;
add += (l+1)/3;
}
int i = first+1;
while(i < last){
if(s[i]=='0'){
int j = i;
while(j <= last && s[j]=='0') j++;
int l = j - i;
add += l/3;
i = j;
}else{
i++;
}
}
cout<<init + add<<'\n';
}
return 0;
}三.本周总结
总体来说这周不错,周六日稍有懈怠了,下周继续努力,下周搞一下dp,牛客要开始了,好好打,over!