线性代数是构建现代计算机科学,特别是图形学和人工智能的核心数学模型。它的核心思想是用向量 (Vector) 来表示数据,用矩阵 (Matrix) 来表示对数据的变换规则。
以下是一个经典的线性代数模型示例,展示了如何使用矩阵将一个二维向量进行旋转变换。
1. 数据表示:向量 (The Vector as Data)
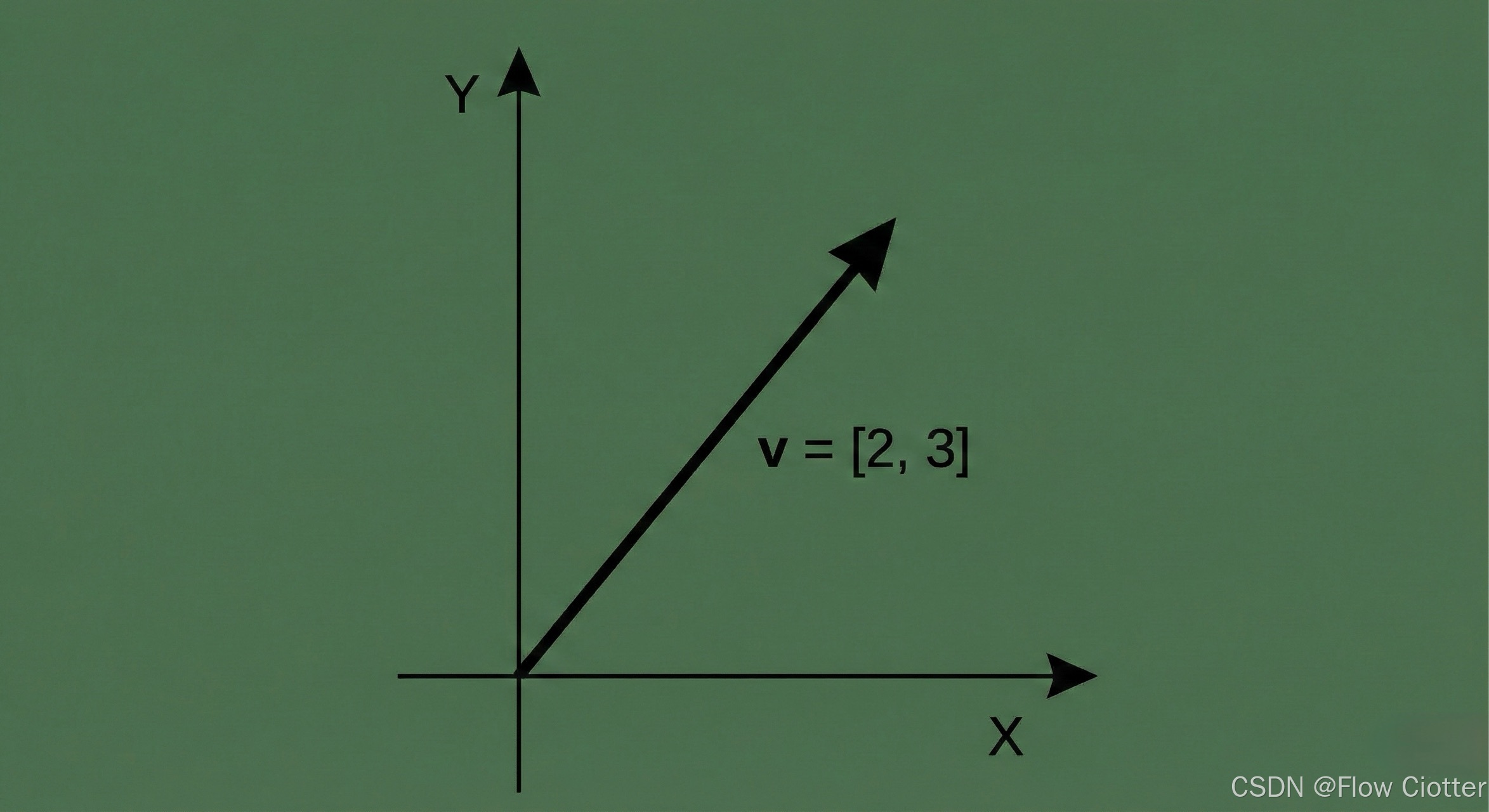
首先,我们需要一种方式来表示我们的原始数据。在二维空间中,一个点的位置可以用一个从原点出发的箭头来表示,这就是向量。
在下图中,我们有一个向量 v,它的坐标是 [2, 3]。这可以代表一个物体的初始位置、一个特征数据点等。
2. 变换规则:矩阵 (The Matrix as Transformation)
接下来,我们需要定义一个规则来改变我们的数据。在 3D 游戏或图像处理中,我们经常需要对物体进行旋转、缩放或平移。这些操作都可以用一个矩阵来表示。
下图展示了一个 2x2 的矩阵 A。这个特定的矩阵代表了一个逆时针旋转 90 度的变换规则。
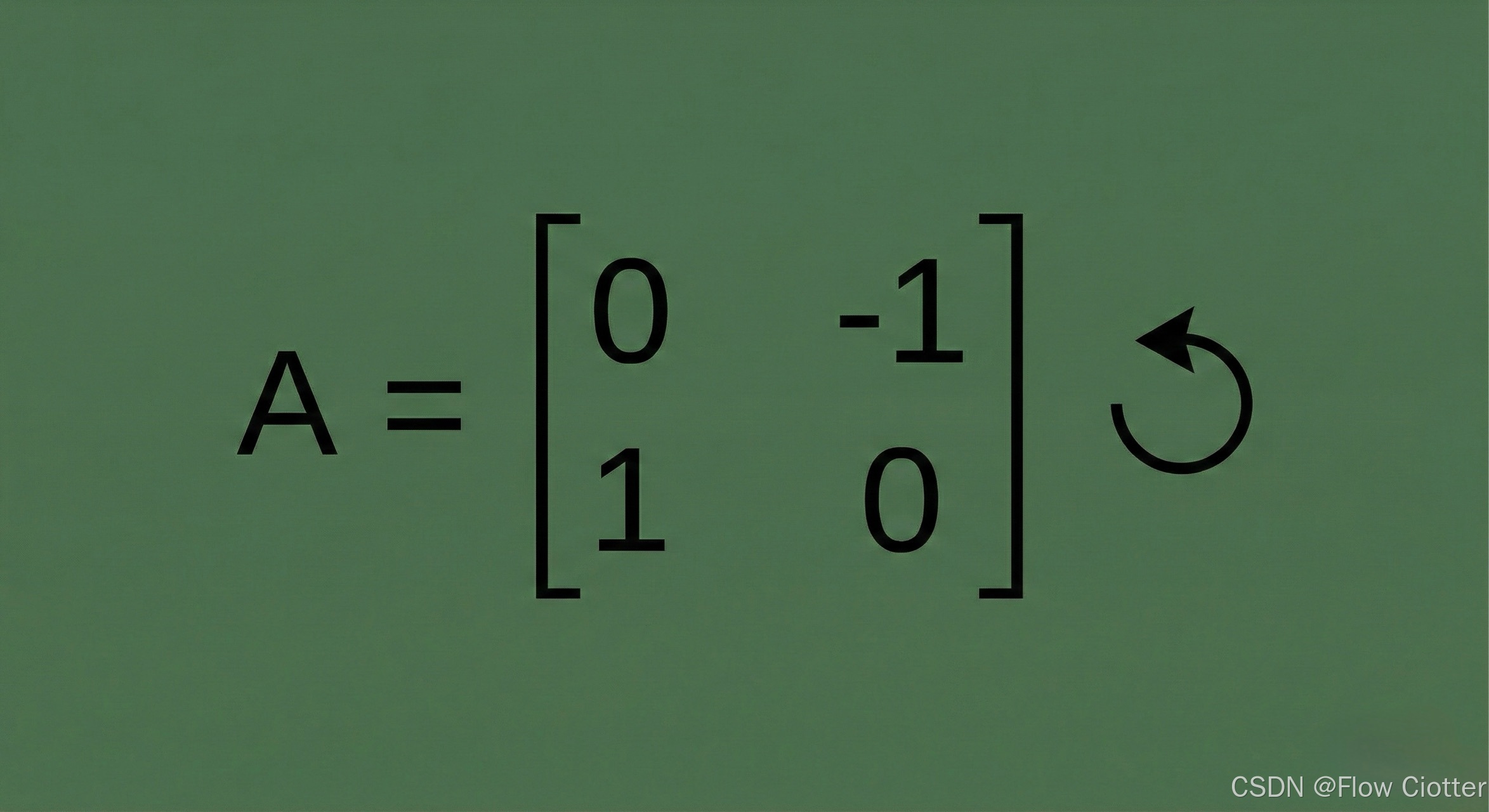
3. 模型应用:矩阵-向量乘法 (Applying the Model)
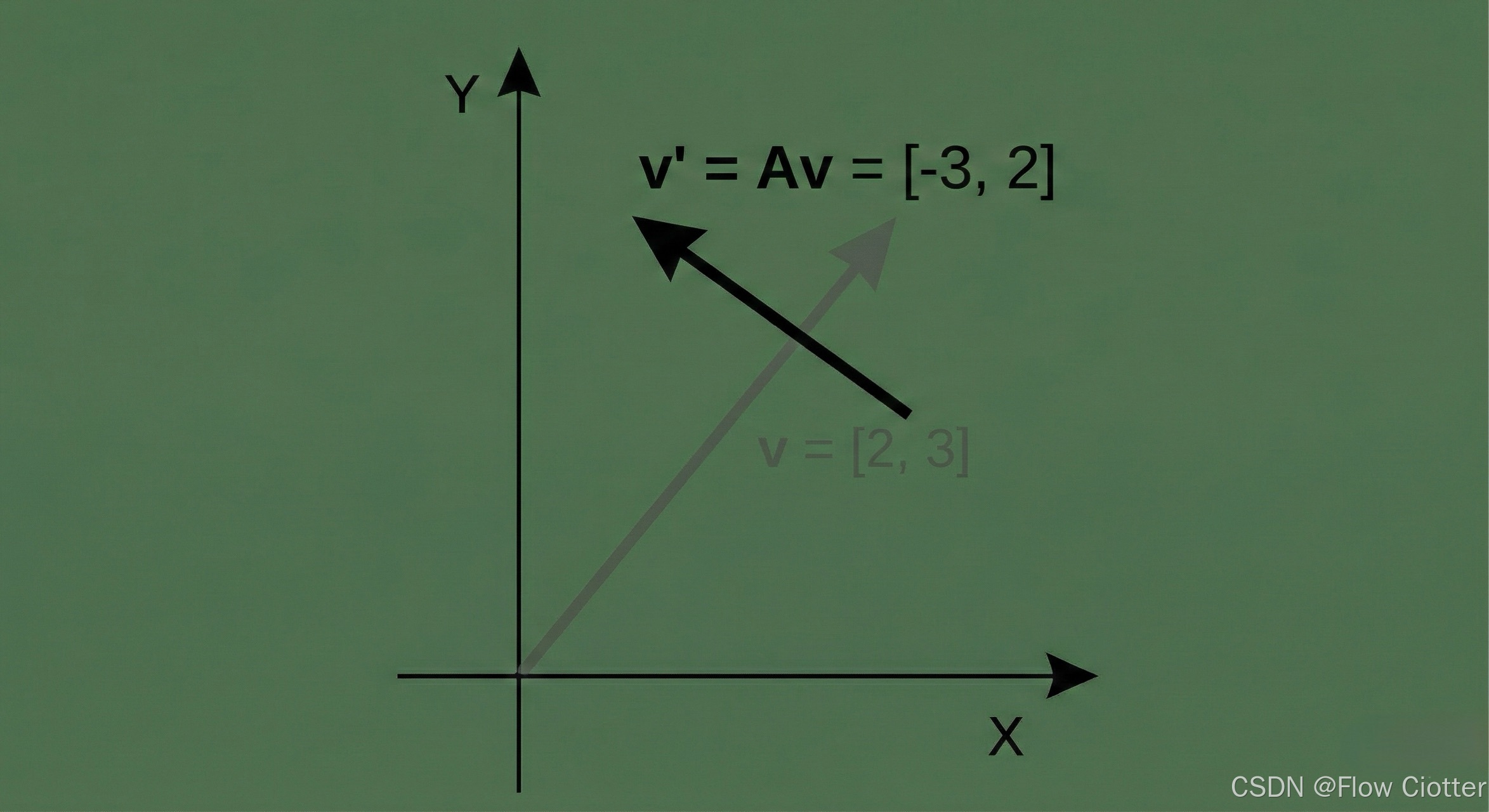
最后,我们将变换规则应用到数据上。这是通过矩阵与向量的乘法 (A 与 v 相乘) 来实现的,其结果是一个新的向量 v'。
在下图中,我们可以看到原始的灰色向量 = [2, 3]经过矩阵 A 的变换后,变成了新的黑色向量 v' = [-3, 2]。可以看到,新的向量正是原向量逆时针旋转 90 度的结果。
这就是一个完整的线性代数数学模型:通过矩阵乘法运算,将一种状态(原始向量)确定性地转换为另一种状态(变换后的向量)。