【大学院-筆記試験練習：线性代数和数据结构（22）】

大学院-筆記試験練習：线性代数和数据结构（22）

1-前言
2-线性代数-题目
3-线性代数-参考答案
4-数据结构-题目
【問題1】連結リストの実装と操作（相似①）
【問題2】ソートアルゴリズムの性質（相似②）
【問題3】スタックとキューの操作列（予測①）
【問題4】探索アルゴリズムと実装（予測②）
5-数据结构-参考答案
[二、【问1】连结リスト（Linked List）](#二、【问1】连结リスト（Linked List）)
- （1）在问什么？（中文）
- - [✅ 日文答案（评分点写法）](#✅ 日文答案（评分点写法）)
- （2）在问什么？（中文）
- - 思路（你脑中要这样想）
  - [✅ 日文答案](#✅ 日文答案)
- （3）在问什么？（中文）
- - 合并过程（你心里要这样走）
  - [✅ 日文答案（按顺序）](#✅ 日文答案（按顺序）)
- （4）在问什么？（中文）
- - [✅ 日文答案（评分点）](#✅ 日文答案（评分点）)
三、【问2】排序算法
- 题目在干嘛？（中文）
- （1）
- - [✅ 日文答案](#✅ 日文答案)
- （2）
- - [✅ 日文答案](#✅ 日文答案)
- （3）
- - [✅ 日文答案](#✅ 日文答案)
四、【问3】哈希（Hashing）
- （1）在问什么？（中文）
- - 实际算一遍（关键）
  - [✅ 日文答案](#✅ 日文答案)
- （2）在问什么？（中文）
- - 关键理解
  - [✅ 日文答案](#✅ 日文答案)
【問題1】連結リスト
- - 你写的：
  - 这题在问什么（再确认一次）
  - [✅ (1) 是否正确？](#✅ (1) 是否正确？)
  - [⚠️ (2) 是否正确？](#⚠️ (2) 是否正确？)
  - - 标准写法（建议你改成这样）：
【問題2】ソートアルゴリズム
- [(1) 你写：](#(1) 你写：)
- - 题目要求：
  - [✅ 判断](#✅ 判断)
- [(2) 你写：](#(2) 你写：)
- - [⚠️ 这里是**唯一一个"有风险"的地方**](#⚠️ 这里是唯一一个“有风险”的地方)
  - - 正确逻辑应该是：
    - 各算法性质：
  - [❌ 风险点](#❌ 风险点)
  - [✅ 标准答案写法](#✅ 标准答案写法)
- [(3) 你写：](#(3) 你写：)
- - 条件：
  - [⚠️ 是否完整？](#⚠️ 是否完整？)
  - 判分习惯：
【問題3】スタック／キュー
- - 我帮你复盘一次（你是怎么想对的）
  - [(1) スタック（LIFO）](#(1) スタック（LIFO）)
  - [(2) キュー（FIFO）](#(2) キュー（FIFO）)
【問題4】DFS
- [(1) 你写的核心意思是：](#(1) 你写的核心意思是：)
- - [✅ 是否正确？](#✅ 是否正确？)
- [(2) 你写：](#(2) 你写：)
- - 条件：
  - [✅ 判断](#✅ 判断)
6-总结

1-前言

为了升到自己目标的大学院，所作的努力和学习，这里是线性代数和数据结构部分。

2-线性代数-题目

3-线性代数-参考答案

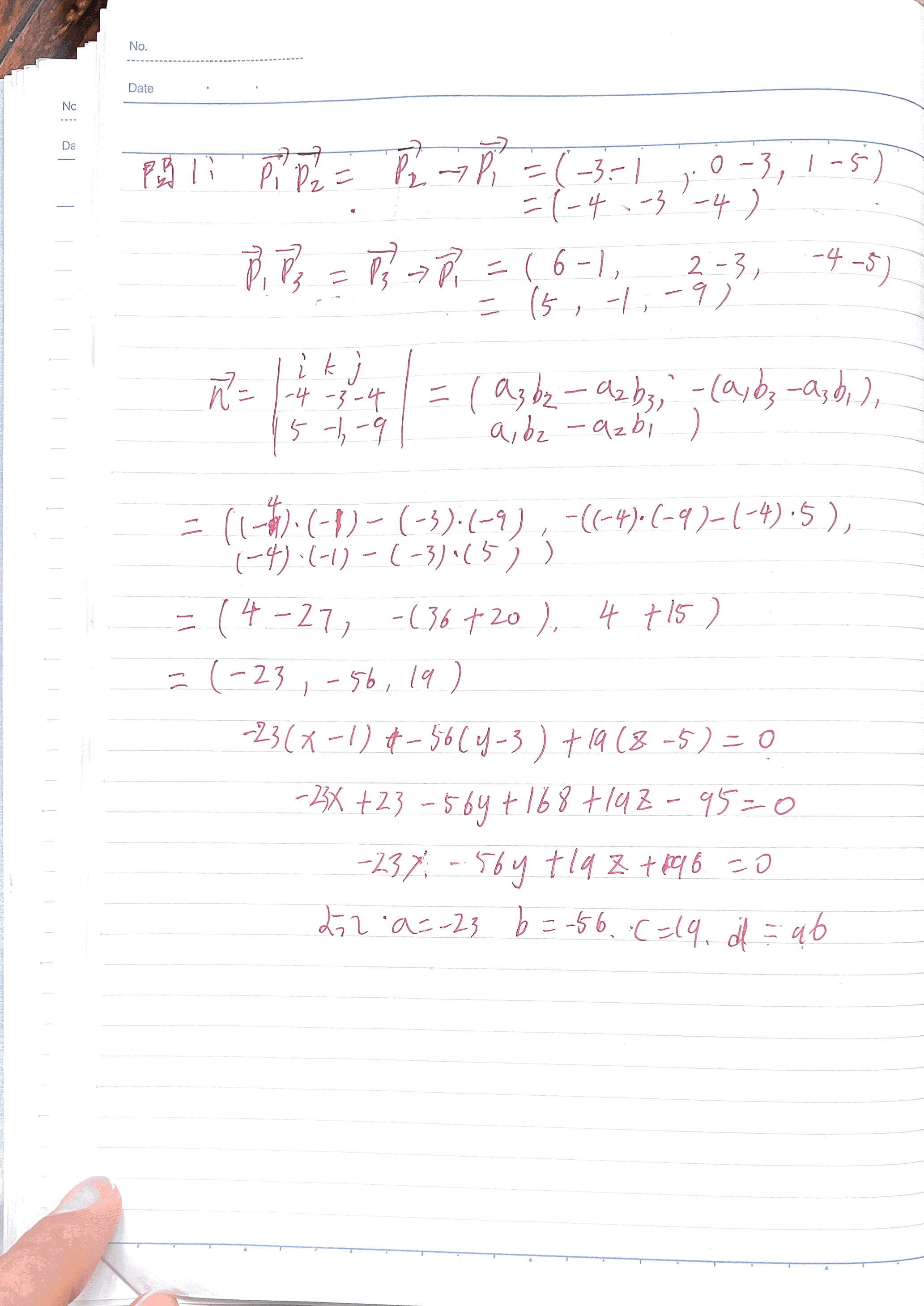
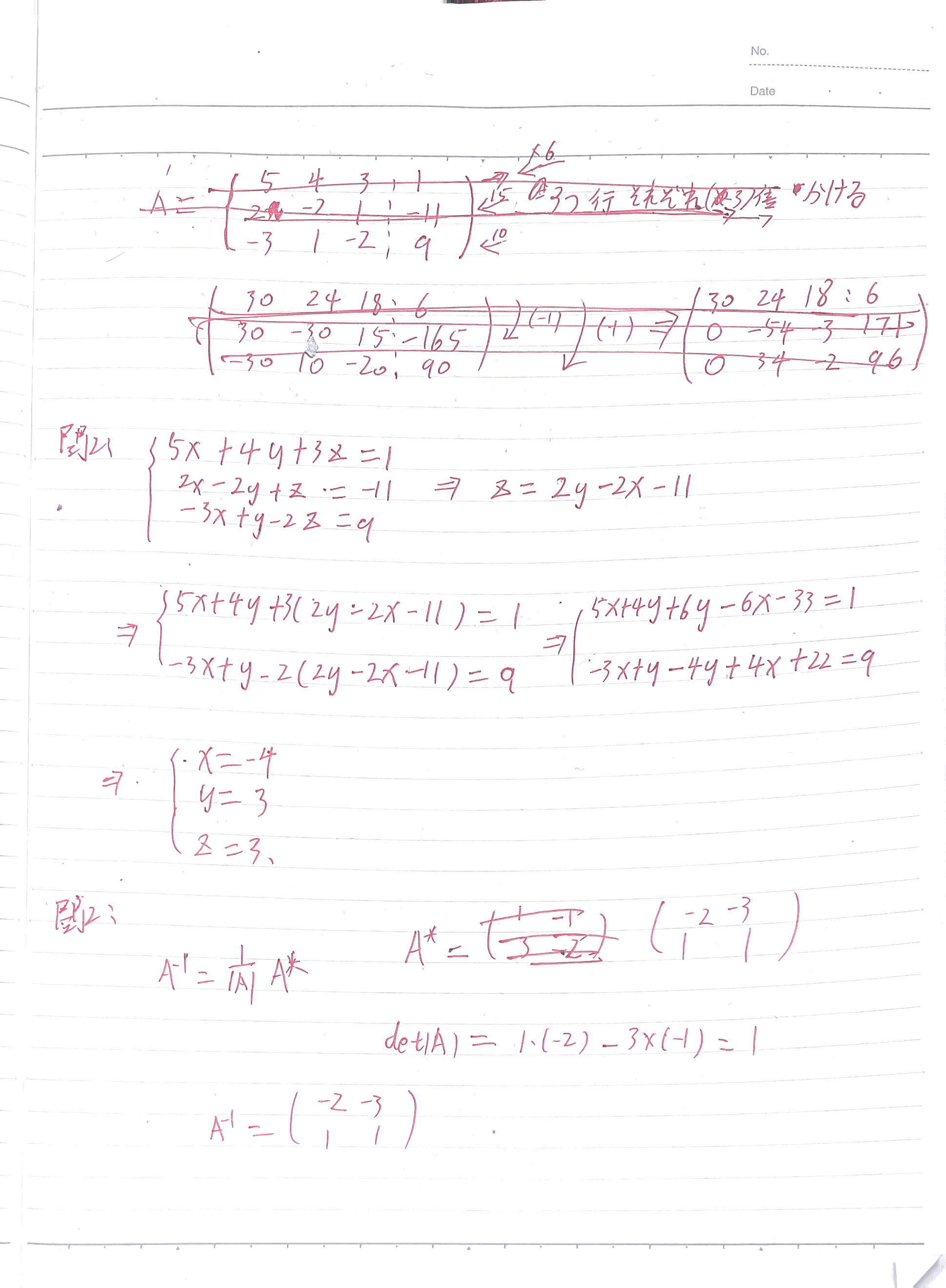
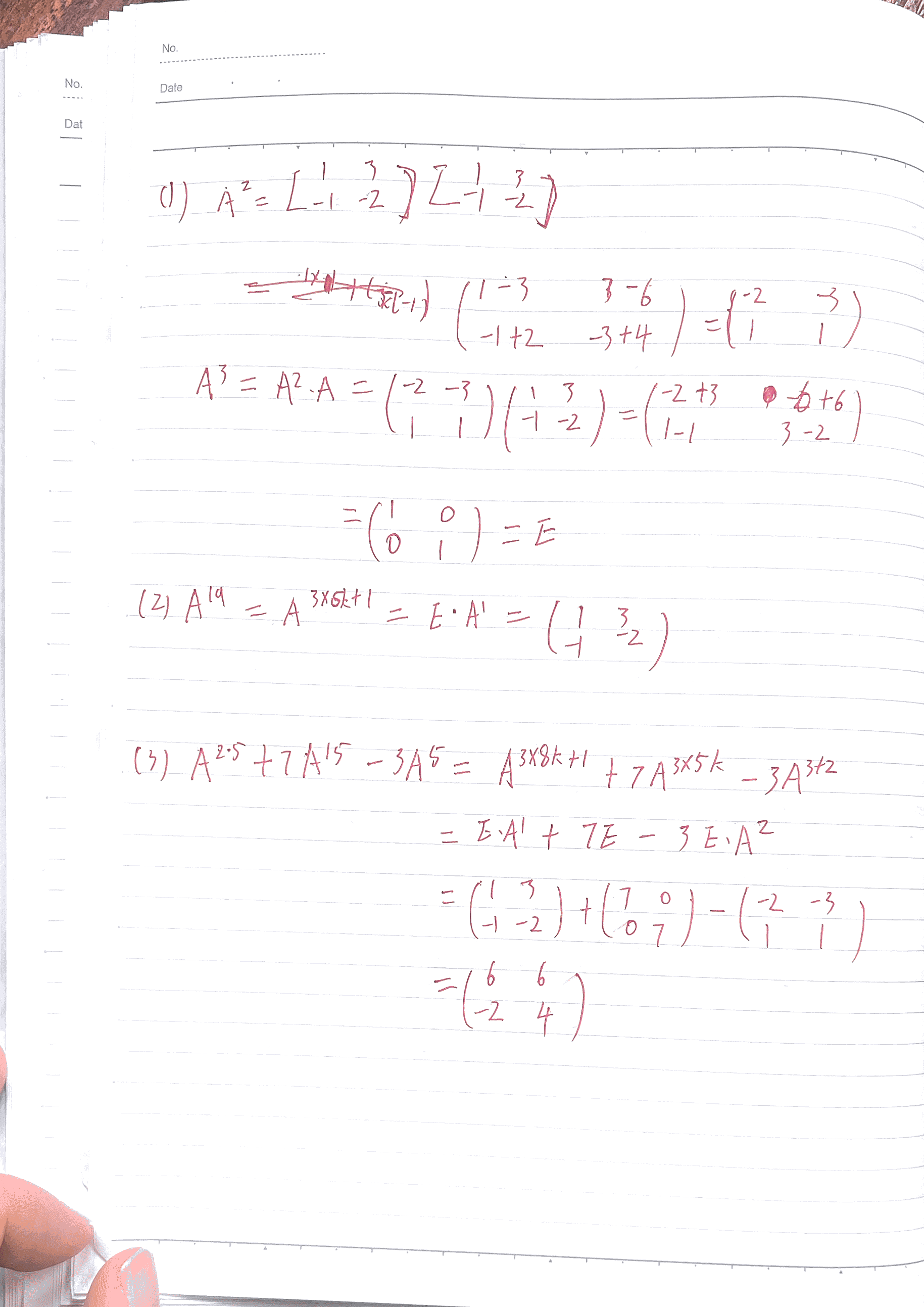
4-数据结构-题目

【問題1】連結リストの実装と操作（相似①）

n 個の整数 (x_1, x_2, \dots, x_n) からなる連結リストを，

以下の実装方法 A および実装方法 B により実現する。

実装方法A：先頭要素への参照のみを保持する。
実装方法B：先頭要素への参照と末尾要素への参照の両方を保持する。

以下の問いに答えよ。

(1)

実装方法Bにより実現された連結リストにおいて，

「新しい要素を末尾に追加し，先頭の要素を削除する」

という操作を繰り返すデータ構造として最も適切なものを答えよ。

(2)

実装方法Aおよび実装方法Bについて，

末尾の要素を参照するために必要な最悪時間計算量 を，

要素数 n を用いてオーダー表記でそれぞれ答えよ。

(3)

実装方法Aで実現された 2 つの連結リスト list1, list2 が与えられる。

list1 および list2 はいずれも降順に整列されている。

次の処理により，2 つの連結リストを 1 つに統合したとき，

得られる連結リストの要素を先頭から順にすべて示せ。

（※ 擬似コード省略）

【問題2】ソートアルゴリズムの性質（相似②）

要素数 n の配列を昇順にソートするアルゴリズムについて考える。

以下の問いに答えよ。

(1)
最悪時間計算量が (O(n \log n)) であり，

かつ 安定なソートであるアルゴリズムの名称を 1 つ答えよ。

(2)
最悪時間計算量が (O(n^2)) であり，

かつ 不安定なソートであるアルゴリズムをすべて答えよ。

(3)
最悪時間計算量が (O(n^2)) であり，

かつ 安定なソートであるアルゴリズムをすべて答えよ。

【問題3】スタックとキューの操作列（予測①）

空のデータ構造 D に対して，以下の操作をこの順に行う。

push(3)
push(5)
pop()
push(7)
pop()
pop()

(1)

D が スタック として実装されているとき，

pop 操作によって取り出される値を，出現順にすべて示せ。

(2)

D が キュー として実装されているとき，

pop（dequeue）操作によって取り出される値を，出現順にすべて示せ。

【問題4】探索アルゴリズムと実装（予測②）

連結な無向グラフ (G = (V, E)) に対して，

深さ優先探索（DFS）を行うことを考える。

(1)

DFS を再帰呼び出し によって実装する場合と，
明示的なスタック を用いて実装する場合について，

探索順序が一致するかどうかを簡潔に述べよ。

(2)

隣接リスト表現を用いた DFS の*

5-数据结构-参考答案

二、【问1】连结リスト（Linked List）

（1）在问什么？（中文）

用实现方法B （有 top 指向头、rear 指向尾）

新元素 加在末尾

删除 从头部删

这种"行为模式"对应哪一种抽象数据结构？

👉 本质：

先进先出（FIFO）
尾进、头出

✅ 日文答案（评分点写法）

① キュー

（2）在问什么？（中文）

在实现方法A / B中，
"寻找末尾元素"

最坏情况下要花多少时间？

思路（你脑中要这样想）

方法A：只有 top，不知道尾巴在哪
→ 只能从头一个一个走
方法B：有 rear，直接指向尾

✅ 日文答案

実装方法A：
$O(n)$
実装方法B：
$O(1)$

（3）在问什么？（中文）

给了你两个按降序排列的连结リスト：

list1：7 → 5 → 3
list2：6 → 4

函数 searchTwoList 的作用是：

👉 把两个"已排序的链表"合并成一个"已排序的链表"

合并过程（你心里要这样走）

比较 7 和 6 → 选 7
比较 5 和 6 → 选 6
比较 5 和 4 → 选 5
比较 3 和 4 → 选 4
剩下 3

✅ 日文答案（按顺序）

7 → 6 → 5 → 4 → 3

（4）在问什么？（中文）

上面这个"合并两个链表"的函数

在最坏情况下要比较多少次？

👉 每次递归都会"至少删掉一个节点"

👉 两个表全部扫完为止

✅ 日文答案（评分点）

O(n + m)

（n：list1 的元素数，m：list2 的元素数）

三、【问2】排序算法

题目在干嘛？（中文）

不是问你"这个算法是什么"，

而是：

给你「最坏时间复杂度 + 是否稳定」
→ 让你反推出"有哪些算法符合"

（1）

最坏时间 O(n log n) 且稳定

✅ 日文答案

⑤ マージソート

（2）

最坏时间 O(n²) 且不安定

✅ 日文答案

② 選択ソート，⑥ クイックソート

（注意：快速排序在最坏情况下是 n²，且不稳定）

（3）

最坏时间 O(n²) 且安定

✅ 日文答案

① バブルソート，③ 挿入ソート

四、【问3】哈希（Hashing）

（1）在问什么？（中文）

哈希函数：
$h(a) = a \\bmod 3$
从前往后插入，第一个发生冲突的是谁？

实际算一遍（关键）

元素	mod 3
10	1
5	2
6	0
4	1 ← ⚠️ 和 10 冲突

✅ 日文答案

4

（2）在问什么？（中文）

如果完全没有冲突 ，

查找一个元素最坏要多久？

关键理解

无冲突 = 直接定位
不需要遍历

✅ 日文答案

O(1)

【問題1】連結リスト

你写的：

(1) キュー

(2) O(n), O(1)

这题在问什么（再确认一次）

实现方法B
- 末尾追加
- 先头删除
  → 行为是否符合某种抽象数据结构？

✅ (1) 是否正确？

✔ 完全正确

原因（评分点逻辑）：

尾进（enqueue）
头出（dequeue）
FIFO

👉 答案关键词就是 キュー

⚠️ (2) 是否正确？

你写的是：

O(n), O(1)

结论：逻辑正确，但考试上必须"分开写清楚"

标准写法（建议你改成这样）：

実装方法A：O(n)
実装方法B：O(1)

📌 为什么要分开？

非常在意**"哪个实现 → 哪个复杂度"**

只写一串 O(n), O(1) 有时会被认为"不严谨"。

【問題2】ソートアルゴリズム

(1) 你写：

マージソート

题目要求：

最悪時間計算量：O(n log n)
安定

✅ 判断

✔ 完全正确

マージソート：
- 最坏 O(n log n)
- 安定
  👉 这是标准答案

(2) 你写：

選択ソート、クイックソート、バブルソート（被你划掉）

⚠️ 这里是唯一一个"有风险"的地方

正确逻辑应该是：

条件：
- 最悪 O(n²)
- 不安定

各算法性质：

算法	最坏	安定性
選択ソート	O(n²)	❌ 不安定
クイックソート	O(n²)	❌ 不安定
バブルソート	O(n²)	✅ 安定

👉 バブルソート不应该出现

❌ 风险点

你虽然划掉了バブルソート ，

但如果考试中写出来再划，有被当"答案不明确"扣分的可能。

✅ 标准答案写法

選択ソート，クイックソート

(3) 你写：

挿入ソート

条件：

最坏 O(n²)
安定

⚠️ 是否完整？

理论上还缺一个

算法	是否满足
挿入ソート	✅
バブルソート	✅

判分习惯：

如果题目写「すべて答えよ」
- ❌ 少一个 = 扣分
如果题目写「答えよ」
- ⚠️ 有时给部分分

📌 稳妥写法（推荐）：

挿入ソート，バブルソート

【問題3】スタック／キュー

你写的：

(1) [5, 7, 3]

(2) [3, 5, 7]

我帮你复盘一次（你是怎么想对的）

操作序列是：

复制代码

push(3)
push(5)
pop()
push(7)
pop()
pop()

(1) スタック（LIFO）

pop 顺序：
5 → 7 → 3

✔ 你写的正确

(2) キュー（FIFO）

pop 顺序：
3 → 5 → 7

✔ 你写的正确

【問題4】DFS

(1) 你写的核心意思是：

DFS 用递归时，调用栈就是隐式的 stack

用显式 stack 时，本质相同，顺序一致

✅ 是否正确？

✔ 完全正确，而且是高分答案

喜欢的关键词你基本都写出来了：

再帰呼び出し
スタック
処理順序が一致

📌 如果更"满分化"，可以补一句：

隣接頂点の処理順が同一である場合

(2) 你写：

O(n + m)

条件：

DFS
隣接リスト

✅ 判断

✔ 完全正确

6-总结

训练成长。！！