Flutter for OpenHarmony 进阶：表达式解析算法与计算器核心实现

一起养小猫2026-02-03 11:51

Flutter for OpenHarmony 进阶：表达式解析算法与计算器核心实现

文章目录

摘要

表达式解析是计算器应用的核心技术，涉及字符串分析、语法解析、数值计算等多个领域。本文深入讲解表达式解析算法的实现原理，详细介绍中缀表达式转后缀表达式、双栈求值算法、浮点数精度处理等高级技术点。通过本文学习，读者将掌握计算器核心算法的完整实现方案，了解如何构建高效、准确的表达式解析系统。

一、表达式解析概述

1.1 表达式类型

中缀表达式

  • 运算符位于操作数中间
  • 符合人类书写习惯
  • 需要处理运算符优先级
  • 示例：3 + 4 × 5

后缀表达式（逆波兰表示法）

  • 运算符位于操作数后面
  • 不需要括号和优先级
  • 易于计算机处理
  • 示例：3 4 5 × +

前缀表达式

  • 运算符位于操作数前面
  • Lisp语言采用此表示法
  • 示例：+ 3 × 4 5

1.2 运算符优先级

优先级 运算符 结合性
1 () 从左到右
2 × ÷ % 从左到右
3 + - 从左到右

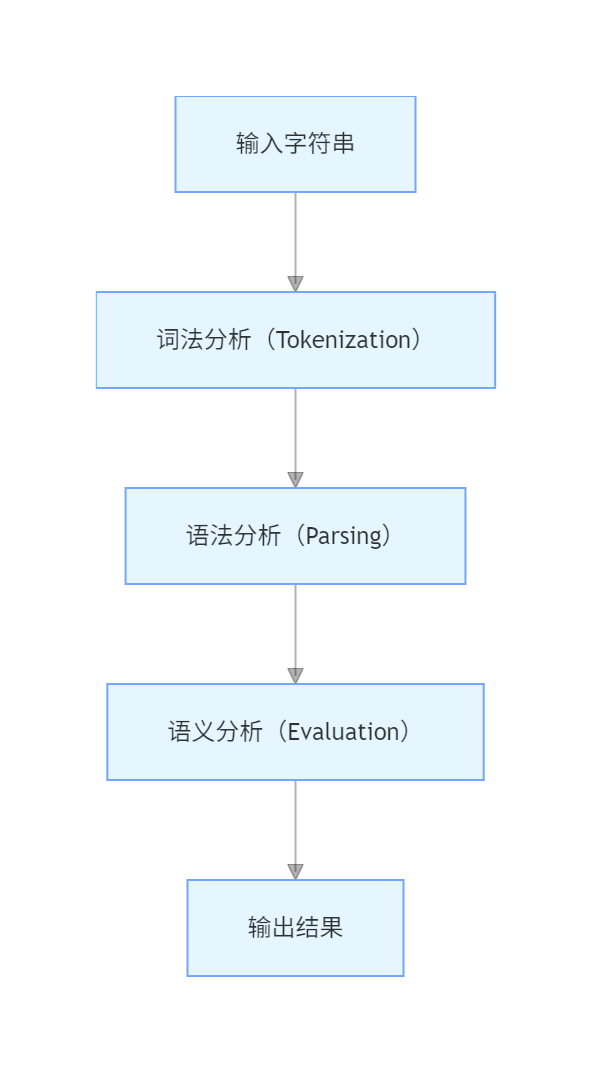
1.3 解析流程

二、中缀表达式转后缀表达式

2.1 转换算法（调度场算法）

dart 复制代码 
class ShuntingYardAlgorithm {
  // 运算符优先级
  int getPrecedence(String operator) {
    switch (operator) {
      case '+':
      case '-':
        return 1;
      case '×':
      case '÷':
      case '%':
        return 2;
      default:
        return 0;
    }
  }

  // 判断是否为运算符
  bool isOperator(String token) {
    return ['+', '-', '×', '÷', '%'].contains(token);
  }

  // 中缀转后缀
  List<String> infixToPostfix(List<String> infixTokens) {
    List<String> output = [];
    List<String> operatorStack = [];

    for (var token in infixTokens) {
      if (isOperator(token)) {
        // 处理运算符
        while (operatorStack.isNotEmpty &&
            isOperator(operatorStack.last) &&
            getPrecedence(operatorStack.last) >= getPrecedence(token)) {
          output.add(operatorStack.removeLast());
        }
        operatorStack.add(token);
      } else if (token == '(') {
        // 左括号直接入栈
        operatorStack.add(token);
      } else if (token == ')') {
        // 右括号：弹出直到左括号
        while (operatorStack.isNotEmpty && operatorStack.last != '(') {
          output.add(operatorStack.removeLast());
        }
        if (operatorStack.isNotEmpty) {
          operatorStack.removeLast(); // 移除左括号
        }
      } else {
        // 操作数直接输出
        output.add(token);
      }
    }

    // 弹出栈中剩余运算符
    while (operatorStack.isNotEmpty) {
      output.add(operatorStack.removeLast());
    }

    return output;
  }
}

2.2 词法分析

dart 复制代码 
class Lexer {
  // 将表达式字符串转换为Token列表
  static List<String> tokenize(String expression) {
    List<String> tokens = [];
    StringBuffer numberBuffer = StringBuffer();

    for (int i = 0; i < expression.length; i++) {
      String char = expression[i];

      if (isDigit(char) || char == '.') {
        // 数字字符，添加到数字缓冲区
        numberBuffer.write(char);
      } else {
        // 非数字字符
        if (numberBuffer.isNotEmpty) {
          tokens.add(numberBuffer.toString());
          numberBuffer.clear();
        }
        if (char.trim().isNotEmpty) {
          tokens.add(char);
        }
      }
    }

    // 添加最后一个数字
    if (numberBuffer.isNotEmpty) {
      tokens.add(numberBuffer.toString());
    }

    return tokens;
  }

  static bool isDigit(String char) {
    return char.codeUnitAt(0) >= '0'.codeUnitAt(0) &&
        char.codeUnitAt(0) <= '9'.codeUnitAt(0);
  }
}

2.3 完整转换示例

dart 复制代码 
void main() {
  final algorithm = ShuntingYardAlgorithm();

  // 示例：3 + 4 × 5
  final infix = ['3', '+', '4', '×', '5'];
  final postfix = algorithm.infixToPostfix(infix);

  print('中缀: $infix');
  print('后缀: $postfix');
  // 输出: 中缀: [3, +, 4, ×, 5]
  //      后缀: [3, 4, 5, ×, +]
}

三、后缀表达式求值

3.1 求值算法

dart 复制代码 
class PostfixEvaluator {
  // 后缀表达式求值
  double evaluate(List<String> postfixTokens) {
    List<double> stack = [];

    for (var token in postfixTokens) {
      if (_isNumber(token)) {
        // 操作数入栈
        stack.add(double.parse(token));
      } else if (_isOperator(token)) {
        // 运算符：弹出两个操作数进行计算
        if (stack.length < 2) {
          throw ArgumentError('表达式无效');
        }

        double b = stack.removeLast();
        double a = stack.removeLast();
        double result = _applyOperator(a, b, token);
        stack.add(result);
      }
    }

    if (stack.length != 1) {
      throw ArgumentError('表达式无效');
    }

    return stack.last;
  }

  bool _isNumber(String token) {
    return double.tryParse(token) != null;
  }

  bool _isOperator(String token) {
    return ['+', '-', '×', '÷', '%'].contains(token);
  }

  double _applyOperator(double a, double b, String operator) {
    switch (operator) {
      case '+':
        return a + b;
      case '-':
        return a - b;
      case '×':
        return a * b;
      case '÷':
        if (b == 0) {
          throw ArgumentError('除数不能为零');
        }
        return a / b;
      case '%':
        return a % b;
      default:
        throw ArgumentError('未知运算符: $operator');
    }
  }
}

3.2 求值过程示例

复制代码 
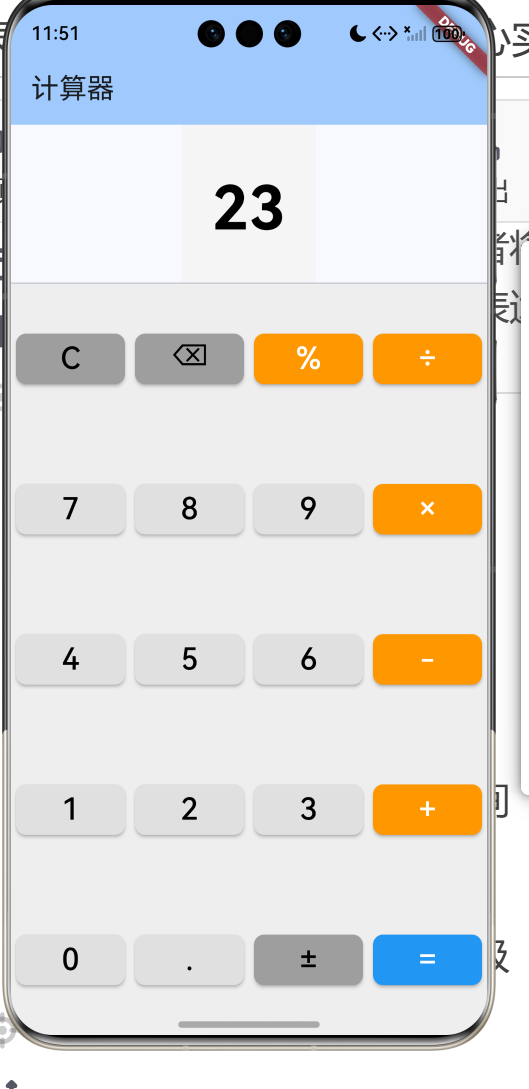
表达式：3 4 5 × +
步骤：
1. 3 → 栈: [3]
2. 4 → 栈: [3, 4]
3. 5 → 栈: [3, 4, 5]
4. × → 弹出5, 4，计算 4×5=20 → 栈: [3, 20]
5. + → 弹出20, 3，计算 3+20=23 → 栈: [23]

结果: 23

四、双栈算法实现

4.1 一次遍历算法

dart 复制代码 
class ExpressionParser {
  // 运算符栈和操作数栈
  List<double> _operandStack = [];
  List<String> _operatorStack = [];

  // 运算符优先级
  int _getPrecedence(String op) {
    switch (op) {
      case '+':
      case '-':
        return 1;
      case '×':
      case '÷':
      case '%':
        return 2;
      default:
        return 0;
    }
  }

  // 判断是否需要计算
  bool _shouldCalculate(String newOperator) {
    if (_operatorStack.isEmpty) return false;
    String topOperator = _operatorStack.last;
    return _getPrecedence(topOperator) >= _getPrecedence(newOperator);
  }

  // 执行一次计算
  void _calculate() {
    if (_operandStack.length < 2 || _operatorStack.isEmpty) {
      return;
    }

    double b = _operandStack.removeLast();
    double a = _operandStack.removeLast();
    String operator = _operatorStack.removeLast();

    double result;
    switch (operator) {
      case '+':
        result = a + b;
        break;
      case '-':
        result = a - b;
        break;
      case '×':
        result = a * b;
        break;
      case '÷':
        if (b == 0) {
          throw ArgumentError('除数不能为零');
        }
        result = a / b;
        break;
      case '%':
        result = a % b;
        break;
      default:
        throw ArgumentError('未知运算符: $operator');
    }

    _operandStack.add(result);
  }

  // 解析并计算表达式
  double parse(String expression) {
    _operandStack.clear();
    _operatorStack.clear();

    List<String> tokens = Lexer.tokenize(expression);

    for (var token in tokens) {
      double? number = double.tryParse(token);
      if (number != null) {
        // 操作数入栈
        _operandStack.add(number);
      } else if (['+', '-', '×', '÷', '%'].contains(token)) {
        // 运算符：先计算高优先级运算
        while (_shouldCalculate(token)) {
          _calculate();
        }
        _operatorStack.add(token);
      }
    }

    // 计算剩余运算
    while (_operatorStack.isNotEmpty) {
      _calculate();
    }

    if (_operandStack.length != 1) {
      throw ArgumentError('表达式无效');
    }

    return _operandStack.last;
  }
}

4.2 支持括号的算法

dart 复制代码 
class AdvancedExpressionParser {
  List<double> _operandStack = [];
  List<String> _operatorStack = [];

  int _getPrecedence(String op) {
    if (op == '(') return 0;
    switch (op) {
      case '+':
      case '-':
        return 1;
      case '×':
      case '÷':
      case '%':
        return 2;
      default:
        return 0;
    }
  }

  void _calculate() {
    if (_operandStack.length < 2 || _operatorStack.isEmpty) return;

    double b = _operandStack.removeLast();
    double a = _operandStack.removeLast();
    String operator = _operatorStack.removeLast();

    double result = _applyOperator(a, b, operator);
    _operandStack.add(result);
  }

  double _applyOperator(double a, double b, String operator) {
    switch (operator) {
      case '+':
        return a + b;
      case '-':
        return a - b;
      case '×':
        return a * b;
      case '÷':
        return b == 0 ? double.nan : a / b;
      case '%':
        return a % b;
      default:
        throw ArgumentError('未知运算符: $operator');
    }
  }

  double parse(String expression) {
    _operandStack.clear();
    _operatorStack.clear();

    List<String> tokens = Lexer.tokenize(expression);

    for (var token in tokens) {
      double? number = double.tryParse(token);
      if (number != null) {
        _operandStack.add(number);
      } else if (token == '(') {
        _operatorStack.add(token);
      } else if (token == ')') {
        // 计算直到遇到左括号
        while (_operatorStack.isNotEmpty && _operatorStack.last != '(') {
          _calculate();
        }
        _operatorStack.removeLast(); // 移除左括号
      } else if (['+', '-', '×', '÷', '%'].contains(token)) {
        while (_operatorStack.isNotEmpty &&
            _operatorStack.last != '(' &&
            _getPrecedence(_operatorStack.last) >= _getPrecedence(token)) {
          _calculate();
        }
        _operatorStack.add(token);
      }
    }

    // 计算剩余运算
    while (_operatorStack.isNotEmpty) {
      _calculate();
    }

    return _operandStack.last;
  }
}

五、浮点数精度处理

5.1 浮点数精度问题

dart 复制代码 
void precisionDemo() {
  print(0.1 + 0.2); // 0.30000000000000004
  print(0.3 - 0.1); // 0.19999999999999998
  print(1.2 × 3);   // 3.5999999999999996
}

5.2 精度处理方案

方案一：四舍五入
dart 复制代码 
class PrecisionHandler {
  static const int DEFAULT_PRECISION = 10;

  // 四舍五入到指定精度
  static double round(double value, int precision) {
    double factor = pow(10, precision).toDouble();
    return (value * factor).roundToDouble() / factor;
  }

  // 智能格式化
  static String format(double value) {
    // 检查是否为整数
    if (value == value.truncateToDouble()) {
      return value.toInt().toString();
    }

    // 四舍五入
    double rounded = round(value, DEFAULT_PRECISION);

    // 检查四舍五入后是否为整数
    if (rounded == rounded.truncateToDouble()) {
      return rounded.toInt().toString();
    }

    // 转换为字符串并移除尾部零
    String result = rounded.toString();
    if (result.contains('.')) {
      result = result.replaceAll(RegExp(r'0+$'), '');
      result = result.replaceAll(RegExp(r'\.$'), '');
    }

    return result;
  }
}
方案二：使用BigInt
dart 复制代码 
class BigIntCalculator {
  // 位数
  final int scale;

  BigIntCalculator({this.scale = 10});

  // 转换为BigInt
  BigInt toBigInt(double value) {
    return (value * pow(10, scale)).toInt().toBigInt();
  }

  // 从BigInt转换回double
  double fromBigInt(BigInt value) {
    return value.toInt() / pow(10, scale);
  }

  // 加法
  double add(double a, double b) {
    BigInt bigA = toBigInt(a);
    BigInt bigB = toBigInt(b);
    return fromBigInt(bigA + bigB);
  }

  // 乘法
  double multiply(double a, double b) {
    BigInt bigA = toBigInt(a);
    BigInt bigB = toBigInt(b);
    return fromBigInt((bigA * bigB) ~/ BigInt.from(10).pow(scale));
  }
}
方案三：使用decimal包
dart 复制代码 
// pubspec.yaml
dependencies:
  decimal: ^2.3.3

// 代码
import 'package:decimal/decimal.dart';

class DecimalCalculator {
  static String calculate(String a, String b, String operator) {
    Decimal decA = Decimal.parse(a);
    Decimal decB = Decimal.parse(b);

    Decimal result;
    switch (operator) {
      case '+':
        result = decA + decB;
        break;
      case '-':
        result = decA - decB;
        break;
      case '×':
        result = decA * decB;
        break;
      case '÷':
        result = decA / decB;
        break;
      default:
        throw ArgumentError('未知运算符');
    }

    return result.toString();
  }
}

六、高级运算符支持

6.1 幂运算

dart 复制代码 
double power(double base, double exponent) {
  return pow(base, exponent).toDouble();
}

// 添加到运算符判断
String _applyOperator(double a, double b, String operator) {
  switch (operator) {
    // ... 其他运算符
    case '^':
      return power(a, b);
    default:
      throw ArgumentError('未知运算符: $operator');
  }
}

6.2 科学计算函数

dart 复制代码 
class ScientificCalculator {
  // 三角函数
  static double sin(double radians) {
    return dartMath.sin(radians);
  }

  static double cos(double radians) {
    return dartMath.cos(radians);
  }

  static double tan(double radians) {
    return dartMath.tan(radians);
  }

  // 对数函数
  static double log(double value) {
    if (value <= 0) {
      throw ArgumentError('对数的真数必须大于零');
    }
    return dartMath.log(value);
  }

  static double log10(double value) {
    if (value <= 0) {
      throw ArgumentError('对数的真数必须大于零');
    }
    return dartMath.log(value) / dartMath.ln10;
  }

  // 平方根
  static double sqrt(double value) {
    if (value < 0) {
      throw ArgumentError('不能对负数开平方');
    }
    return dartMath.sqrt(value);
  }

  // 阶乘
  static int factorial(int n) {
    if (n < 0) {
      throw ArgumentError('阶乘的参数必须是非负整数');
    }
    if (n <= 1) return 1;
    int result = 1;
    for (int i = 2; i <= n; i++) {
      result *= i;
    }
    return result;
  }
}

6.3 扩展词法分析器

dart 复制代码 
class AdvancedLexer {
  static List<String> tokenize(String expression) {
    List<String> tokens = [];
    StringBuffer buffer = StringBuffer();

    for (int i = 0; i < expression.length; i++) {
      String char = expression[i];

      // 处理函数名
      if (isLetter(char)) {
        buffer.write(char);
        // 读取完整的函数名
        while (i + 1 < expression.length && isLetter(expression[i + 1])) {
          i++;
          buffer.write(expression[i]);
        }
        tokens.add(buffer.toString());
        buffer.clear();
      }
      // 处理数字
      else if (isDigit(char) || char == '.') {
        buffer.write(char);
        while (i + 1 < expression.length &&
            (isDigit(expression[i + 1]) || expression[i + 1] == '.')) {
          i++;
          buffer.write(expression[i]);
        }
        tokens.add(buffer.toString());
        buffer.clear();
      }
      // 处理运算符和括号
      else if (char.trim().isNotEmpty) {
        tokens.add(char);
      }
    }

    return tokens;
  }

  static bool isLetter(String char) {
    return (char.codeUnitAt(0) >= 'A'.codeUnitAt(0) &&
            char.codeUnitAt(0) <= 'Z'.codeUnitAt(0)) ||
        (char.codeUnitAt(0) >= 'a'.codeUnitAt(0) &&
            char.codeUnitAt(0) <= 'z'.codeUnitAt(0));
  }

  static bool isDigit(String char) {
    return char.codeUnitAt(0) >= '0'.codeUnitAt(0) &&
        char.codeUnitAt(0) <= '9'.codeUnitAt(0);
  }
}

七、错误处理机制

7.1 错误类型定义

dart 复制代码 
enum CalculatorErrorType {
  syntaxError,          // 语法错误
  divisionByZero,       // 除以零
  invalidOperator,      // 无效运算符
  mismatchedParentheses, // 括号不匹配
  emptyExpression,      // 空表达式
  overflow,             // 数值溢出
}

class CalculatorError implements Exception {
  final CalculatorErrorType type;
  final String message;

  CalculatorError(this.type, this.message);

  @override
  String toString() => 'CalculatorError: $message';
}

7.2 错误检测

dart 复制代码 
class ErrorDetector {
  // 检查括号是否匹配
  static void checkParentheses(String expression) {
    int count = 0;
    for (var char in expression.split('')) {
      if (char == '(') {
        count++;
      } else if (char == ')') {
        count--;
        if (count < 0) {
          throw CalculatorError(
            CalculatorErrorType.mismatchedParentheses,
            '括号不匹配：右括号过多',
          );
        }
      }
    }

    if (count > 0) {
      throw CalculatorError(
        CalculatorErrorType.mismatchedParentheses,
        '括号不匹配：左括号过多',
      );
    }
  }

  // 检查表达式有效性
  static void validateExpression(String expression) {
    if (expression.trim().isEmpty) {
      throw CalculatorError(
        CalculatorErrorType.emptyExpression,
        '表达式为空',
      );
    }

    // 检查连续运算符
    if (RegExp(r'[+\-×÷%^]{2,}').hasMatch(expression)) {
      throw CalculatorError(
        CalculatorErrorType.syntaxError,
        '连续的运算符',
      );
    }

    // 检查运算符位置
    if (RegExp(r'^[+\-×÷%^]|[+\-×÷%^]$').hasMatch(expression)) {
      throw CalculatorError(
        CalculatorErrorType.syntaxError,
        '运算符位置错误',
      );
    }
  }

  // 检查数值溢出
  static void checkOverflow(double value) {
    if (!value.isFinite) {
      throw CalculatorError(
        CalculatorErrorType.overflow,
        '数值溢出',
      );
    }
  }
}

7.3 友好的错误提示

dart 复制代码 
class ErrorHandler {
  static String getErrorMessage(CalculatorError error) {
    switch (error.type) {
      case CalculatorErrorType.syntaxError:
        return '表达式语法错误';
      case CalculatorErrorType.divisionByZero:
        return '不能除以零';
      case CalculatorErrorType.invalidOperator:
        return '无效的运算符';
      case CalculatorErrorType.mismatchedParentheses:
        return '括号不匹配';
      case CalculatorErrorType.emptyExpression:
        return '请输入表达式';
      case CalculatorErrorType.overflow:
        return '数值过大或过小';
    }
  }

  static String getUserFriendlyMessage(dynamic error) {
    if (error is CalculatorError) {
      return getErrorMessage(error);
    } else if (error is ArgumentError) {
      return error.message;
    } else if (error is FormatException) {
      return '数字格式错误';
    } else {
      return '未知错误';
    }
  }
}

八、性能优化策略

8.1 缓存机制

dart 复制代码 
class CachedCalculator {
  final Map<String, double> _cache = {};

  double calculate(String expression) {
    // 检查缓存
    if (_cache.containsKey(expression)) {
      return _cache[expression]!;
    }

    // 计算结果
    double result = _parse(expression);

    // 存入缓存
    _cache[expression] = result;

    return result;
  }

  void clearCache() {
    _cache.clear();
  }
}

8.2 懒惰求值

dart 复制代码 
class LazyEvaluator {
  String? _lastExpression;
  double? _lastResult;

  double evaluate(String expression) {
    // 如果表达式没变，返回上次结果
    if (expression == _lastExpression && _lastResult != null) {
      return _lastResult!;
    }

    // 计算新结果
    double result = _parse(expression);

    // 更新缓存
    _lastExpression = expression;
    _lastResult = result;

    return result;
  }
}

8.3 增量计算

dart 复制代码 
class IncrementalCalculator {
  double? _lastResult;
  String? _lastOperator;

  double calculate(double operand, String? operator) {
    if (_lastResult == null || operator == null) {
      _lastResult = operand;
      return operand;
    }

    double result;
    switch (operator) {
      case '+':
        result = _lastResult! + operand;
        break;
      case '-':
        result = _lastResult! - operand;
        break;
      case '×':
        result = _lastResult! * operand;
        break;
      case '÷':
        result = _lastResult! / operand;
        break;
      default:
        result = operand;
    }

    _lastResult = result;
    return result;
  }

  void reset() {
    _lastResult = null;
    _lastOperator = null;
  }
}

九、总结

本文深入讲解了计算器应用中表达式解析算法的实现技术，主要内容包括：

  1. 表达式类型：中缀、后缀、前缀表达式及其转换
  2. 调度场算法：中缀转后缀的标准算法
  3. 双栈求值：一次遍历完成解析和计算
  4. 浮点数精度：多种精度处理方案
  5. 高级运算符：幂运算、科学计算函数
  6. 错误处理：完善的错误检测和提示机制
  7. 性能优化：缓存、懒惰求值、增量计算

掌握这些技术可以让你开发出功能强大、计算准确的科学计算器。在实际项目中，还需要考虑用户体验、边界条件、性能优化等方面，确保应用的稳定性和可靠性。

欢迎加入开源鸿蒙跨平台社区 : 开源鸿蒙跨平台开发者社区

相关推荐
池央2 小时前
贪心-最长递增子序列
算法·贪心算法
We་ct2 小时前
LeetCode 383. 赎金信：解题思路+代码解析+优化实战
前端·算法·leetcode·typescript
不懒不懒2 小时前
【逻辑回归从原理到实战：正则化、参数调优与过拟合处理】
人工智能·算法·机器学习
一只大袋鼠2 小时前
分布式 ID 生成：雪花算法原理、实现与 MyBatis-Plus 实战
分布式·算法·mybatis
tobias.b2 小时前
408真题解析-2010-27-操作系统-同步互斥/Peterson算法
算法·计算机考研·408真题解析
寄存器漫游者2 小时前
数据结构 二叉树核心概念与特性
数据结构·算法
m0_706653232 小时前
跨语言调用C++接口
开发语言·c++·算法
皮皮哎哟2 小时前
数据结构：从队列到二叉树基础解析
c语言·数据结构·算法·二叉树·队列
一匹电信狗2 小时前
【高阶数据结构】并查集
c语言·数据结构·c++·算法·leetcode·排序算法·visual studio
热门推荐
01GitHub 镜像站点02Clawdbot 中文汉化版 接入微信、飞书03OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)04Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services05OpenClaw部署与配置教程：在Mac mini上接入国产大模型与飞书06UV安装并设置国内源07Claude Code Skills 实用使用手册08在Trae中使用Pencil MCP09Linux下V2Ray安装配置指南102026美赛A题智能手机电池续航时间预测的连续时间数学模型