学习内容
-
PCL ICP 的数学推导(最小二乘 + SVD 闭式解)
-
ICP 全流程(与 PCL 完全一致)
-
MATLAB 完整可运行测试代码(带配准前/后图像)
-
误差曲线(optional)
一、PCL ICP 的数学原理
PCL 使用的是 经典 Point-to-Point ICP:
给定两组点云:
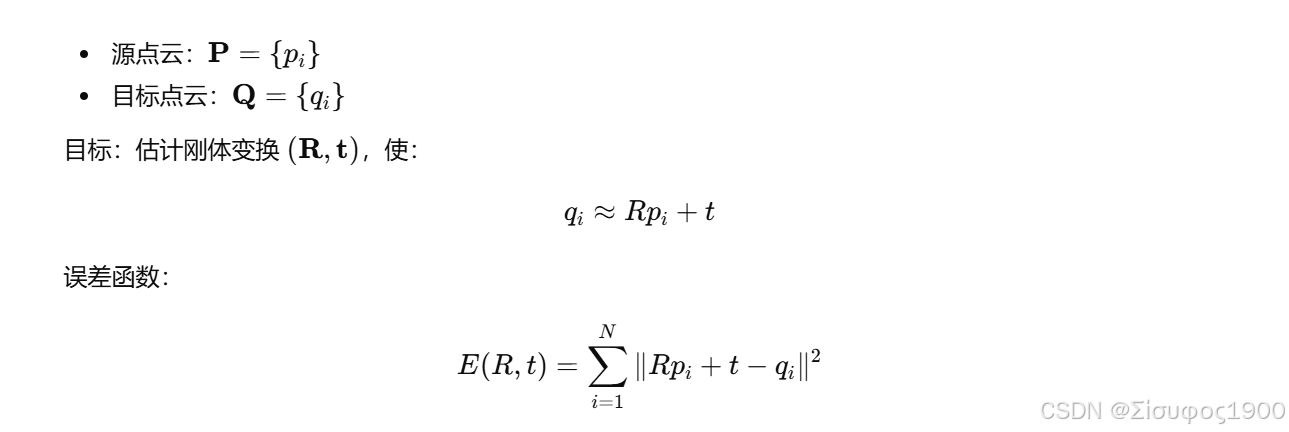
Step 1:去中心化
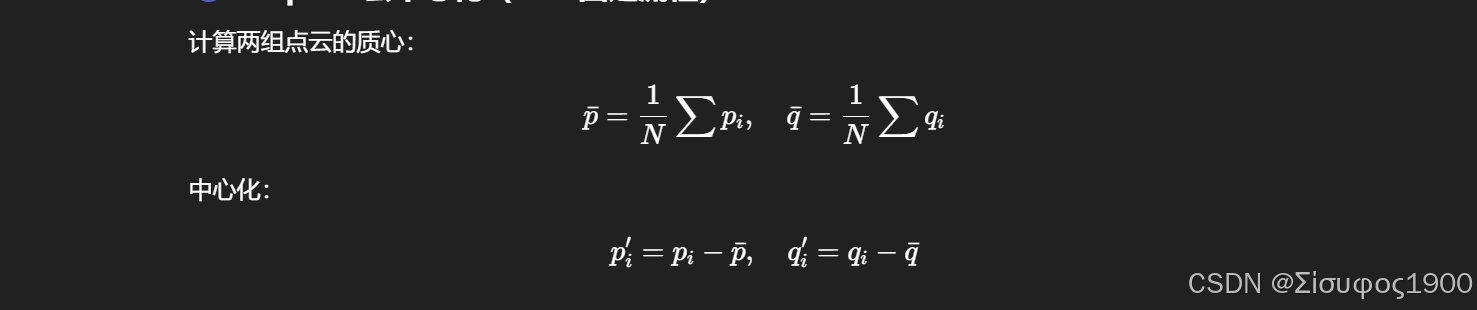
Step 2:构造协方差矩阵
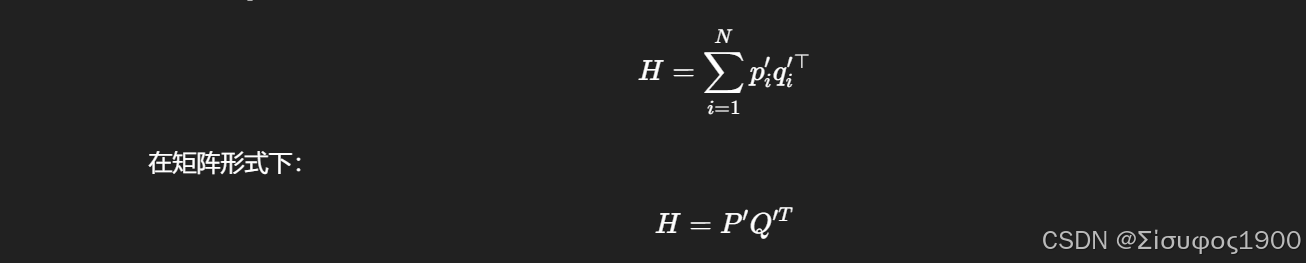
Step 3:SVD 求旋转

Step 4:求平移
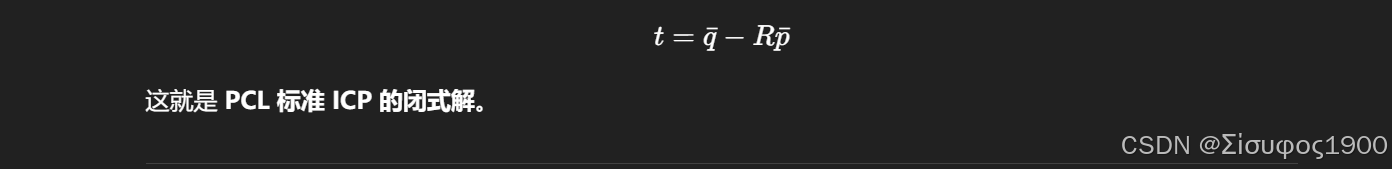
二、ICP 迭代流程
-
找最近邻(PCL 默认使用 Kd-tree)
-
计算质心
-
构造 H

- SVD 求解 R,t
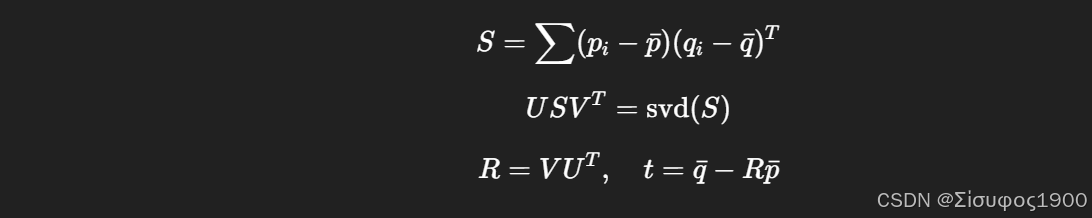
- 变换源点云
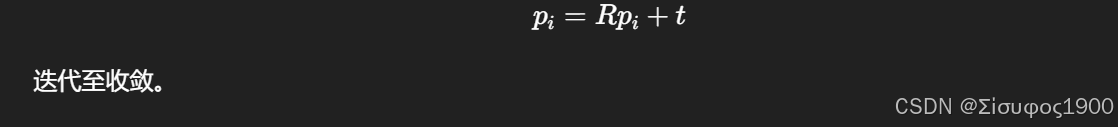
- 判断收敛
三、MATLAB 完整 ICP 代码
代码内容:
-
随机生成点云
-
施加已知 R,t
-
用 ICP 配准
-
显示配准前后结果
案例1
cpp
%% -------- 生成 Bunny-like 点云 --------
N1 = 800;
theta = 2*pi*rand(N1,1);
phi = pi*rand(N1,1);
body = [0.35*sin(phi).*cos(theta), ...
0.2*sin(phi).*sin(theta), ...
0.3*cos(phi)];
N2 = 300;
theta = 2*pi*rand(N2,1);
phi = pi*rand(N2,1);
head = [0.2*sin(phi).*cos(theta), ...
0.2*sin(phi).*sin(theta), ...
0.25*cos(phi) + 0.4];
ear1 = randn(200,3).* [0.05 0.02 0.2] + [0.1 0.05 0.7];
ear2 = randn(200,3).* [0.05 0.02 0.2] + [-0.1 0.05 0.7];
P = [body; head; ear1; ear2]; % 目标点云
%% -------- 增加刚性变换 --------
Rtrue = [0.99 -0.05 0; 0.05 0.99 0; 0 0 1];
ttrue = [0.15 -0.05 0.02];
Q = (Rtrue * P')' + ttrue; % 源点云(被移动)
%% -------- ICP(Point-to-Point)--------
maxIter = 25;
Qk = Q;
R_total = eye(3);
t_total = zeros(3,1);
for iter = 1:maxIter
% --- 最近邻 ---
idx = knnsearch(P, Qk);
P_match = P(idx,:);
% --- 均值 ---
pm = mean(Qk,1);
qm = mean(P_match,1);
% --- 协方差矩阵 ---
S = (Qk - pm)' * (P_match - qm);
% --- SVD 求旋转 ---
[U,~,V] = svd(S);
R = V*U';
if det(R) < 0
V(:,3) = -V(:,3);
R = V*U';
end
% --- 平移 ---
t = qm' - R*pm';
% --- 更新 ---
Qk = (R*Qk')' + t';
R_total = R * R_total;
t_total = R * t_total + t;
end
%% -------- 绘图 --------
figure;
subplot(1,2,1);
scatter3(P(:,1),P(:,2),P(:,3),10,'b'); hold on;
scatter3(Q(:,1),Q(:,2),Q(:,3),10,'r');
title('Before ICP'); axis equal;
subplot(1,2,2);
scatter3(P(:,1),P(:,2),P(:,3),10,'b'); hold on;
scatter3(Qk(:,1),Qk(:,2),Qk(:,3),10,'r');
title('After ICP'); axis equal;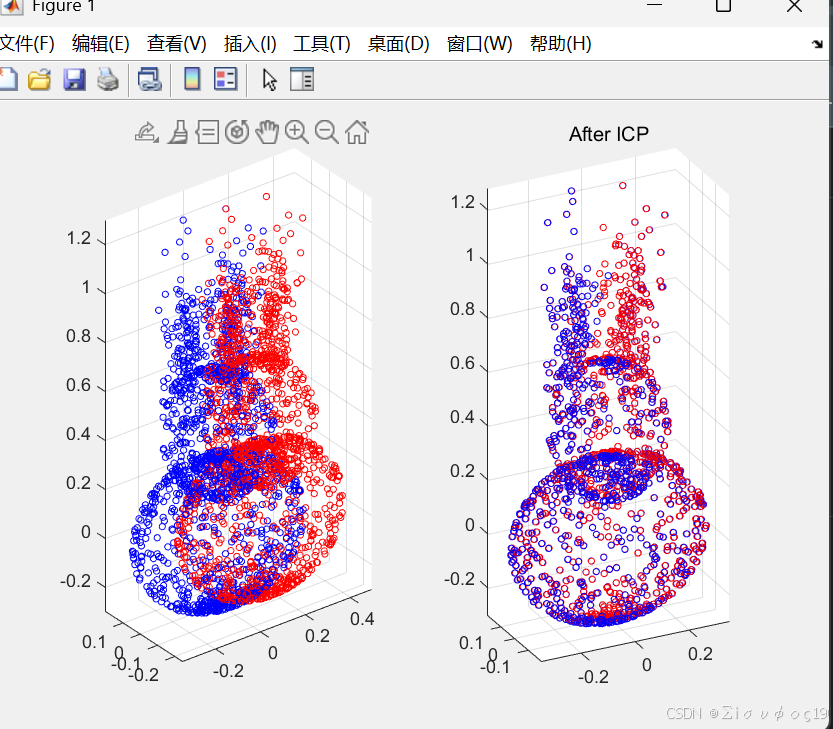
案例2
读取点云:
cpp
ptCloud = pcread('bun000.ply');
P = ptCloud.Location; 给目标电源加旋转和平移
cpp
% 下采样减少计算量(可选)
ptCloud = pcdownsample(ptCloud, 'gridAverage', 0.003);
P = ptCloud.Location;
% 加旋转和平移
Rtrue = axang2rotm([0 0 1 deg2rad(35)]); % 绕 Z 轴 25度
ttrue = [0.22 -0.13 0.31];
Q = (Rtrue * P')' + ttrue; % 源点云(待配准)匹配函数:
cpp
% 最大迭代次数
function [R_total, t_total, Q_aligned] = icp_point2point(P, Q, maxIter)
% 初始化矩阵
Qk = Q;
R_total = eye(3);
t_total = zeros(3,1);
% 开始迭代
for iter = 1:maxIter
% --- 最近邻匹配(kNN) ---
idx = knnsearch(P, Qk);
P_match = P(idx,:);
% --- 计算中心 ---
pm = mean(Qk,1);
qm = mean(P_match,1);
% --- 协方差矩阵 ---
S = (Qk - pm)' * (P_match - qm);
% --- SVD -- 求旋转 ---
[U,~,V] = svd(S);
R = V * U';
% 右手系修正
if det(R) < 0
V(:,3) = -V(:,3);
R = V * U';
end
% --- 平移 ---
t = qm' - R*pm';
% --- 更新 ---
Qk = (R * Qk')' + t';
% 累积
R_total = R * R_total;
t_total = R * t_total + t;
end
Q_aligned = Qk;
end调用
cpp
%% 读取 Stanford Bunny
ptCloud = pcread('bun000.ply');
ptCloud = pcdownsample(ptCloud, 'gridAverage', 0.003);
P = ptCloud.Location;
%% 加模型变换
Rtrue = axang2rotm([0 0 1 deg2rad(35)]);
ttrue = [0.22 -0.13 0.31];
Q = (Rtrue * P')' + ttrue;
%% ICP 配准
[R_est, t_est, Q_icp] = icp_point2point(P, Q, 300);
%% 显示结果
figure;
subplot(1,2,1);
pcshow(pointCloud(P)); hold on;
pcshow(pointCloud(Q)); title('Before ICP'); axis equal;
subplot(1,2,2);
pcshow(pointCloud(P)); hold on;
pcshow(pointCloud(Q_icp)); title('After ICP'); axis equal;
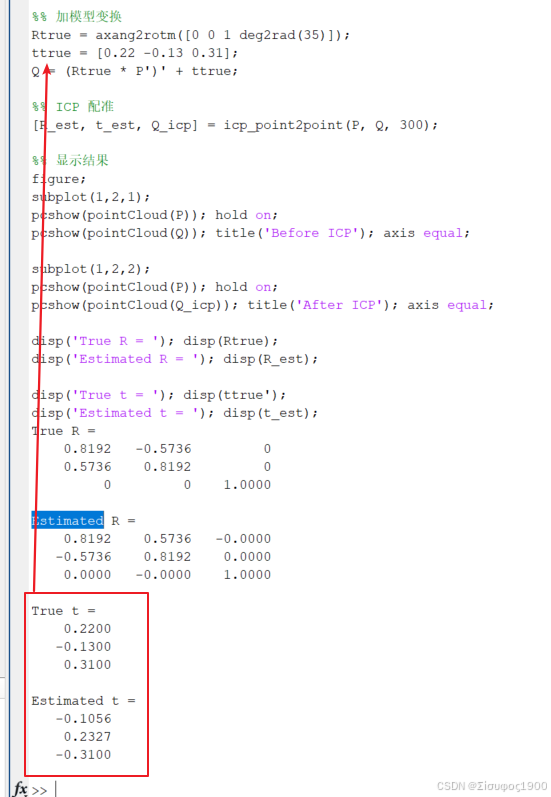
disp('True R = '); disp(Rtrue);
disp('Estimated R = '); disp(R_est);
disp('True t = '); disp(ttrue');
disp('Estimated t = '); disp(t_est);结果显示
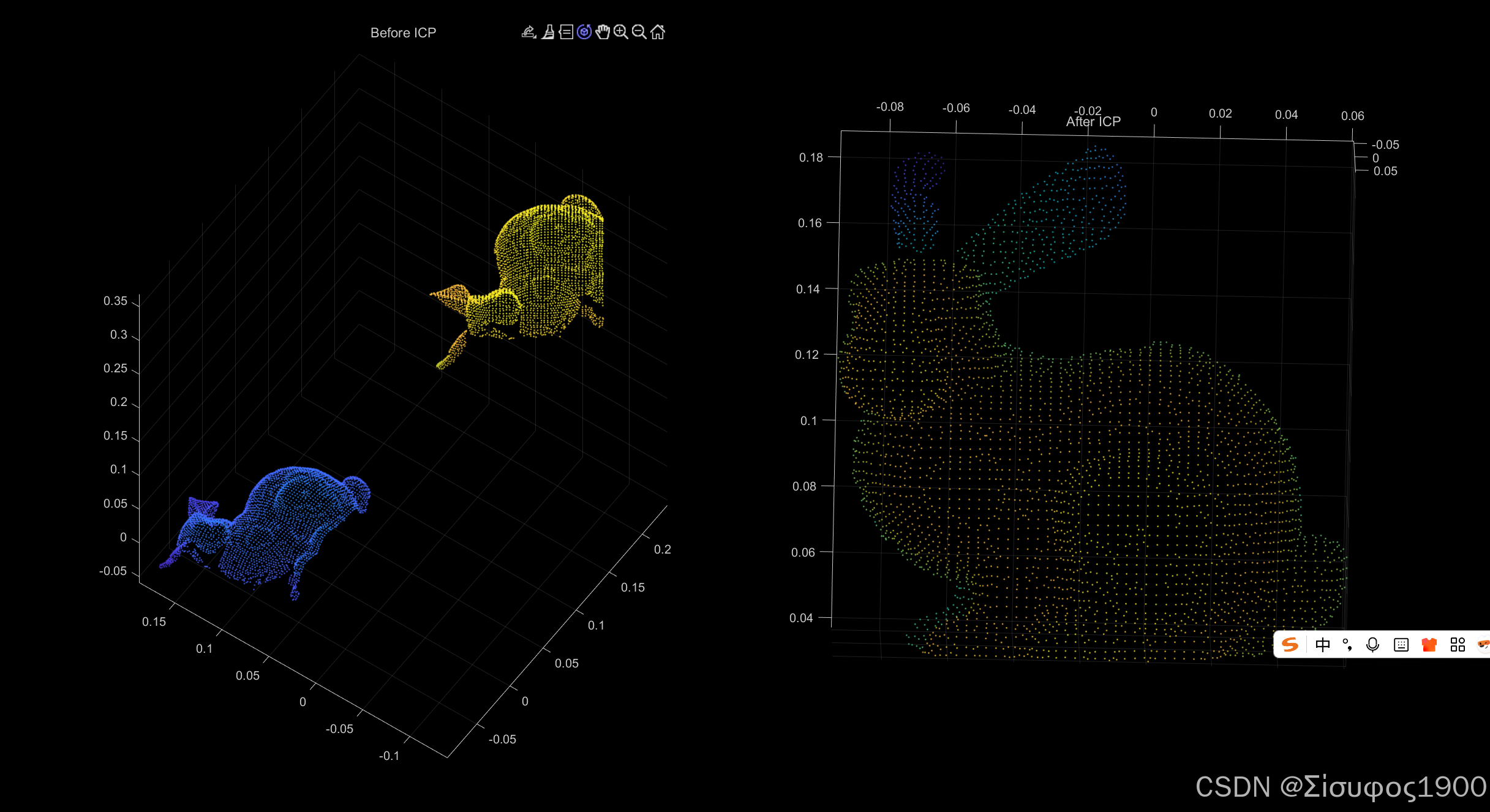
四、解答
1、ICP 中去中心化的目的是什么
目的:消除平移影响,使得旋转 R 可以单独用 SVD 求解。
如果不去中心化:
-
平移 t 会混进协方差矩阵
-
SVD 得到的 R 会出错
-
得到的变换不满足正交约束(失真)
去中心化意味着

为什么不去中心化会导致错误?
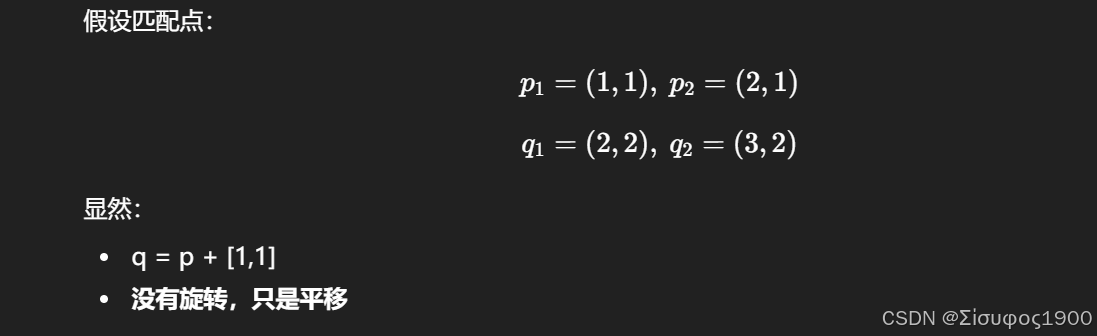
① 不去中心化 S:

得到错误的旋转(明明不该有旋转)
② 去中心化后:

cpp
p = [1 1; 2 1];
q = [2 2; 3 2];
% wrong: without centering
S1 = p' * q;
[U1,S1_,V1] = svd(S1);
R_wrong = V1 * U1'
% correct: with centering
pm = mean(p); qm = mean(q);
p2 = p - pm; q2 = q - qm;
S2 = p2' * q2;
[U2,S2_,V2] = svd(S2);
R_correct = V2 * U2'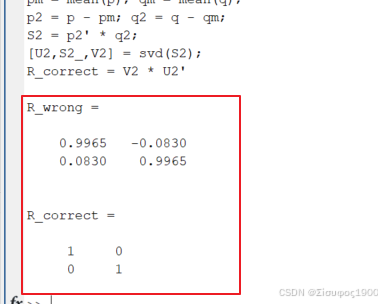
2、ICP 为什么会陷入局部最优
核心原因:ICP 的误差函数是非凸的(non-convex)
Point-to-Point ICP 的误差函数:

ICP 会陷入局部最优的数学原因
原因1:对应关系(最近邻)不是唯一且不连续
对应关系由最近邻决定:

原因2:ICP 只做局部一阶下降(从当前对应开始)
ICP 每次迭代都是:
-
最近邻匹配(固定对应)
-
求刚性最小二乘(确定 R,t)
但对应关系错误 → 输入错误 → 输出"看似正确"的局部最优。
原因3:旋转导致匹配混乱,ICP 找不到正确 NN
比如 Bunny 如果旋转超过 30°:
-
两只耳朵的点匹配到身体
-
身体的点匹配到空白区域
-
协方差矩阵错误,SVD 得到错误旋转
ICP 就收敛到"错误配准"。
原因4:ICP 的误差不是对称的
P→Q 和 Q→P 的误差不同:

原因5:点云遮挡、形状重复、缺失数据造成错误对应
常见例子:
-
桌子四条腿对称 → 多个对齐方式都"差不多"
-
物体缺失部分 → 匹配到错误区域
Matlab测试
cpp
%% -------- 构造 L 型点云 --------
t = (0:0.02:1)';
P = [t, zeros(size(t))]; % 横线
P = [P; zeros(size(t)), t]; % 竖线
%% -------- 目标点云 = 旋转 90° --------
Rtrue = [0 -1; 1 0];
Q = (Rtrue * P')';
%% -------- 初始猜测 = 45° --------
theta0 = deg2rad(45);
R0 = [cos(theta0) -sin(theta0); sin(theta0) cos(theta0)];
P0 = (R0 * P')';
%% -------- ICP 配准 --------
maxIter = 50;
Pk = P0;
for iter = 1:maxIter
idx = knnsearch(Q, Pk);
Qm = Q(idx,:);
pm = mean(Pk);
qm = mean(Qm);
S = (Pk-pm)'*(Qm-qm);
[U,~,V] = svd(S);
R = V*U';
t = qm' - R*pm';
Pk = (R*Pk')' + t';
end
%% -------- 绘图 --------
figure; hold on;
plot(P(:,1),P(:,2),'bo');
plot(Q(:,1),Q(:,2),'ro');
plot(P0(:,1),P0(:,2),'gx');
plot(Pk(:,1),Pk(:,2),'k.');
legend('Original','Target','Initial guess','ICP result');
axis equal;
title('ICP stuck in local minimum');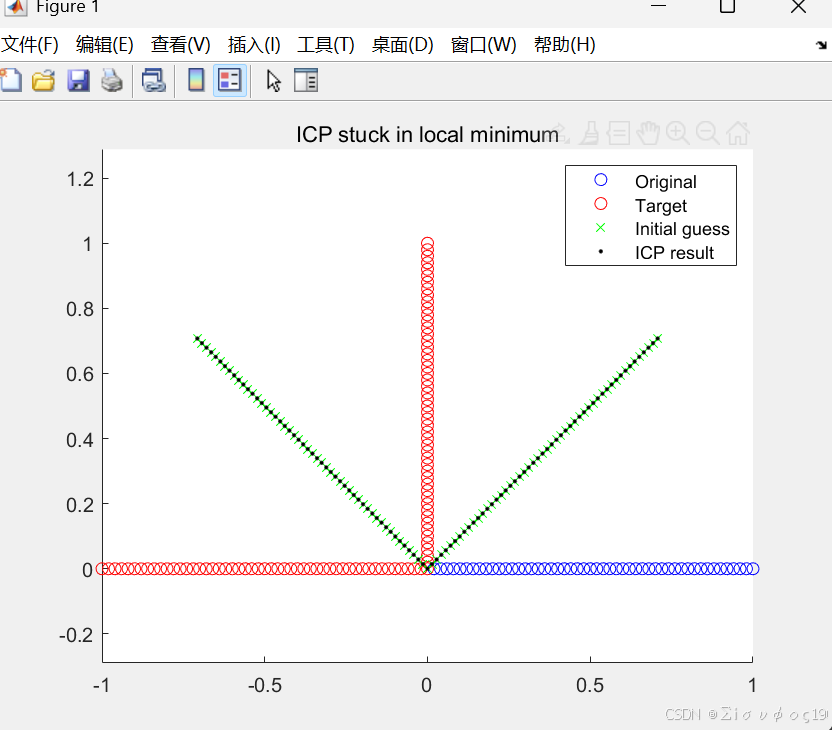
两点云数量差距很大会导致什么
假设源点云 Q 有 10,000 点,目标点云 P 有 100,000 点。
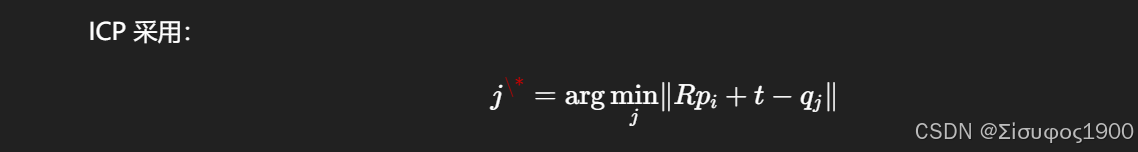
此时会出现:
❌ 1. 目标点云P太密,导致很多 Q 点找到同一个最近邻
→ 匹配矩阵退化
→ 协方差矩阵 S 退化
→ SVD 得到错误旋转 R
→ ICP 震荡或不收敛
❌ 2. 一个源点对应多个目标点,配准偏向目标密集方向
(类似加权错误)
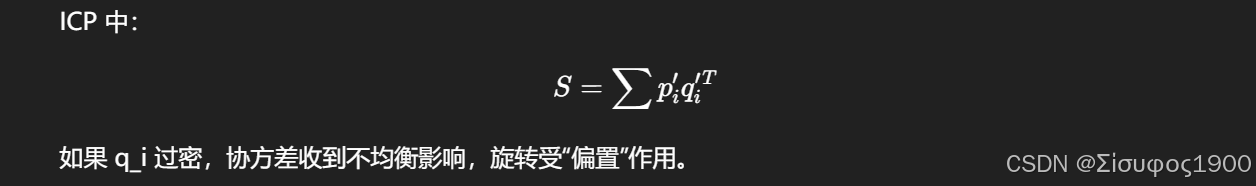
❌ 3. 局部稠密结构(眼睛/耳朵等)相比稀疏区域影响太大
→ 匹配偏向密集区域,可能导致收敛到局部最优
2. 正确做法:保持对应关系的一致性
核心思想:
让参与ICP 的点云具有"对应点分布一致性",而不是数量一致。
不是用等数量点,而是让点的"几何分布"一致。
方案 1:对稠密点云进行体素下采样(最常用)
对点多的那一个点云(通常是 CAD 或扫描后点云)执行:
VoxelGrid(grid_size = 1~5 mm) 保持几何结构但降低密度。
-
点云分布一致
-
最近邻匹配更稳定
-
PCL 默认做法
cpp
ptCloudP = pcdownsample(ptCloudP, 'gridAverage', 0.005);方案 2:均匀采样 / FPS(Furthest Point Sampling)
比 VoxelGrid 的空间分布更均匀。
cpp
idx = fpsSampling(P, 5000); P_fps = P(idx,:);方案 3:基于法向/曲率的重要性采样(保边缘)
稠密区域(平面)采样少
结构区域(边缘/角/曲率大)采样多
用于工业配准(工件边缘)。
方案 4:双向 ICP(Symmetric ICP)
避免"稠密点云方向偏置"导致偏移。
误差改为:
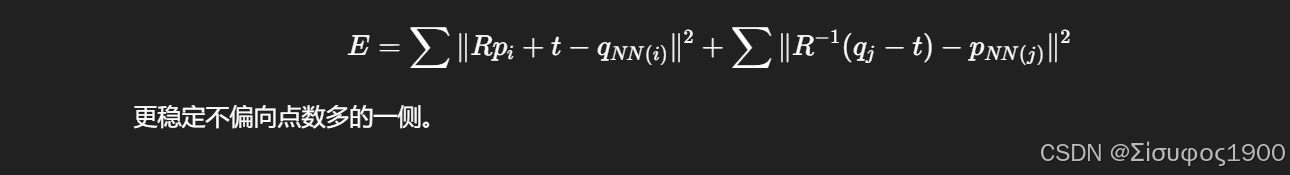
两点云点数差距大时:
| 方法 | 是否解决 |
|---|---|
| 直接 ICP | ❌ 不行,密度差导致匹配偏置 |
| VoxelGrid下采样 | ✅ 最常用 |
| FPS 均匀采样 | ✅ 保结构 |
| 双向 ICP | ✅ 解决密度偏置 |
| 最近邻距离阈值 | ✅ 去掉假匹配 |