在现代遥感与预警系统中,红外小目标检测(IRSTD)被公认为一项极具挑战性的任务 。不同于常规的目标识别,红外图像中的目标往往仅占数个像素,不仅缺乏纹理信息,还极易淹没在复杂的背景噪声与云层干扰中 。为了突破现有技术的瓶颈,西安电子科技大学与重庆邮电大学的研究团队2025 年 12 月 12 日在IEEE Transactions on Image Processing提出了一种名为 WMRNet 的新型网络架构 。本文对其进行解读,补充必要的数学背景,由于论文没有开源代码,我尝试复现核心模块,并封装成可插拔模块。

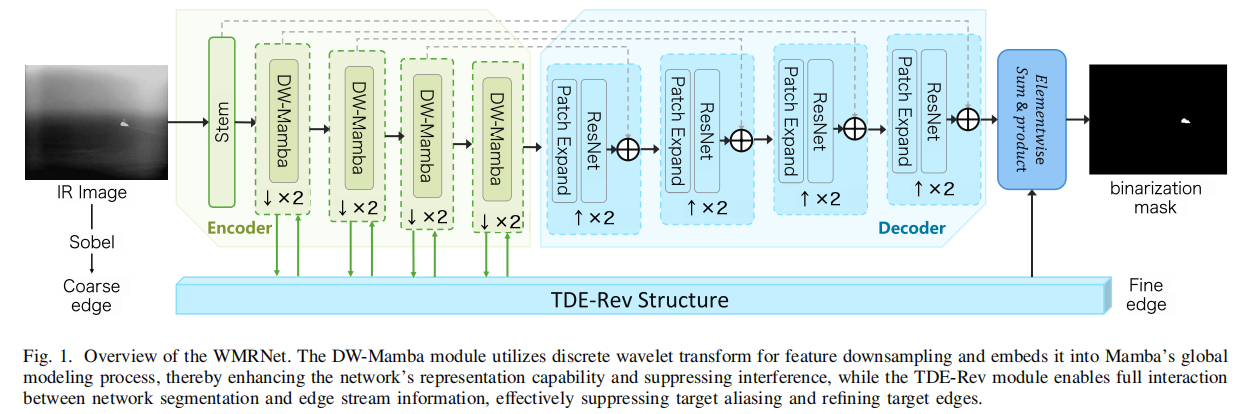
1.核心假设
现有深度学习方法在不断下采样提取特征的过程中,由于采样频率不满足奈奎斯特(Nyquist)采样准则,会不可避免地触发混叠效应(Aliasing Effect),从而导致目标边缘模糊、虚假重影以及信噪比降低 。
2.关键创新
WMRNet 引入了两项关键的数学驱动创新
2.1 离散小波 Mamba 模块(DW-Mamba)
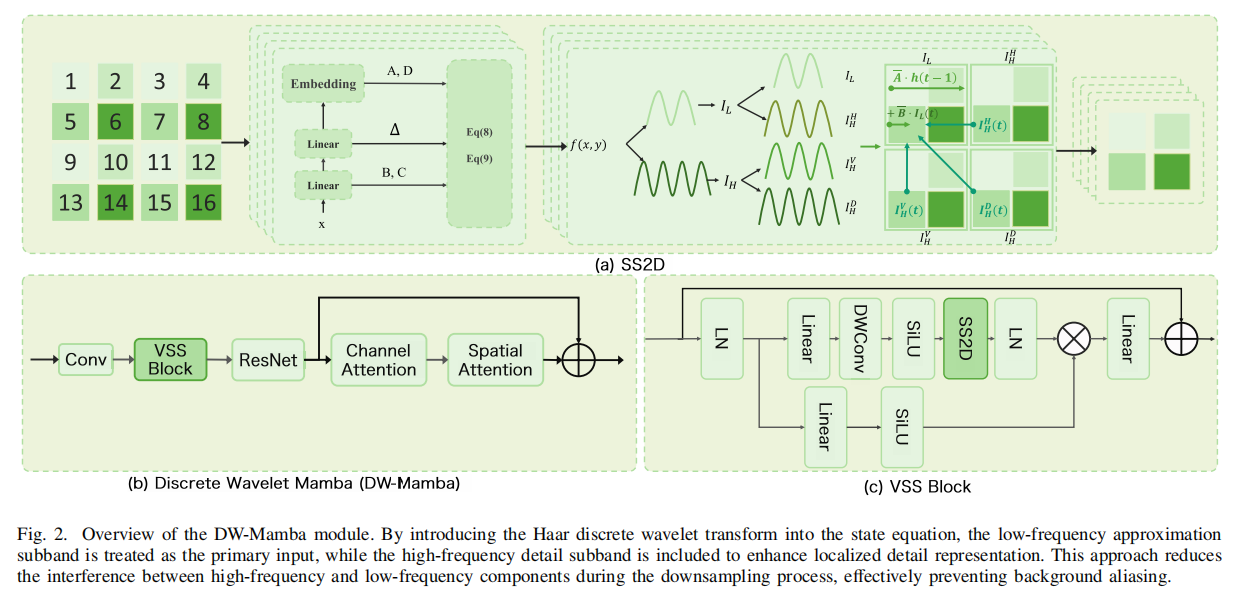
旨在通过频率域的精细分离来抑制背景混叠 。研究团队摒弃了传统的池化或卷积下采样,转而采用二维离散小波变换(2D DWT)将图像分解为低频近似子带 ILI_LIL 与高频细节子带 IHI_HIH 。随后,这些不同频率的分量被深度集成到 Mamba 的状态空间模型(SSM)中,具体集成方式是将 ILI_LIL 作为主输入,将 IHI_HIH 作为状态方程的补充项 。在状态演化过程中,低频分量驱动全局结构的构建,而高频分量则作为状态的实时补偿,确保了微小目标的边缘信息在分辨率降低的过程中依然能够被精确映射 。其核心状态方程描述如下 :
h(t)=A⋅h(t−1)+B⋅IL(t)+IH(t)h(t) = A \cdot h(t-1) + B \cdot I_{L}(t) + I_{H}(t)h(t)=A⋅h(t−1)+B⋅IL(t)+IH(t)
y(t)=C⋅h(t)+D⋅IL(t)y(t) = C \cdot h(t) + D \cdot I_{L}(t)y(t)=C⋅h(t)+D⋅IL(t)
在 DW-Mamba 模块的设计中,作者选择将高频子带 IHI_HIH 作为**恒定系数(常数 1)**引入状态更新方程,一个自然的疑问是为什么不设置为其他系数或为其设置可学习的权重?
个人认为是基于两方面考量:一是抑制噪声放大的风险。红外图像中的高频分量虽然包含了目标的边缘细节,但也集中了大量的背景噪声和杂波 。如果为高频信息设置可学习权重,网络在训练过程中可能会为了拟合某些特定场景的噪声而放大高频系数 。直接以常数 1 引入,本质上是将其作为一种"边缘补充"信号,避免了权重波动导致的检测不稳定 。二是减少参数冗余与计算开销。该设计的初衷是"在不引入额外参数的情况下补充边缘" 。Mamba 架构的优势在于其线性复杂度带来的极快推理速度(WMRNet 推理时间仅 0.010s)。由于状态 h(t)h(t)h(t) 在更新过程中已经融合了这些特征,且输出方程 y(t)y(t)y(t) 并不直接依赖 IHI_HIH,因此不对其设权可以避免冗余计算 。
2.2 三阶差分方程引导的可逆结构(TDE-Rev)
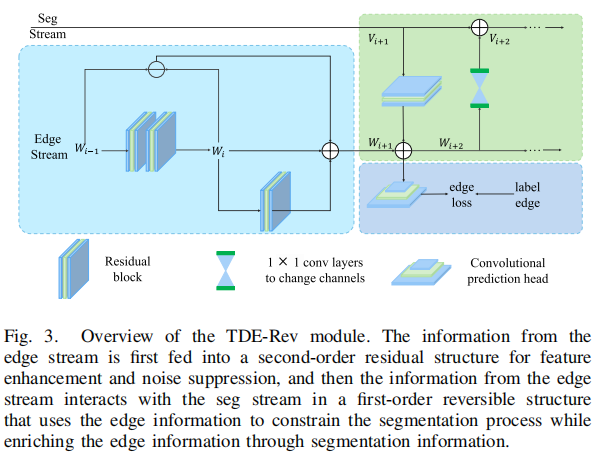
为了进一步精细化目标轮廓并消除边缘混叠,研究团队设计了三阶差分方程引导的可逆结构(TDE-Rev) 。受数值分析中常微分方程(ODE)求解的启发,该模块将边缘提取过程建模为一个高阶差分系统 。通过引入二阶差分项 Δwi=wi−wi−1\Delta w_i = w_i - w_{i-1}Δwi=wi−wi−1 来捕获特征变化的"动量",系统得以在极低对比度的红外背景下,通过高阶导数的敏感性锁定细微的梯度跳变 。同时,利用可逆结构(Reversible Structure)建立起"分割流"与"边缘流"之间的双向高效通道,使边缘细节能够实时约束分割掩码的生成,且无需存储中间激活值,极大地优化了内存效率 。其交互动力学系统可表述为 :
{wi+2=Δwi+wi+l(wi)+g(vi+1)vi+2=vi+1+h(wi+2)\begin{cases}w_{i+2} = \Delta w_{i} + w_{i} + l(w_{i}) + g(v_{i+1}) \\ v_{i+2} = v_{i+1} + h(w_{i+2})\end{cases}{wi+2=Δwi+wi+l(wi)+g(vi+1)vi+2=vi+1+h(wi+2)
这个设计的思想在于双流高效交互:
边缘流 →\to→ 分割流:利用高阶导数提取的精确边缘特征来引导分割过程,抑制虚假边缘 。
分割流 →\to→ 边缘流:分割结果反过来丰富边缘信息 。
这里论文中没有过多解释细节,我估计看论文会有如下几方面疑问:
问题1:为什么需要"三阶"差分?
如果有数字图像处理的知识其实容易理解。在数字图像处理中,通常使用二阶微分算子(如 Laplacian)来定位边缘,因为二阶导数的零交叉点或双峰值能很好地对应强度突变 。红外小目标的信号非常微弱,且常淹没在背景噪声中,导致传统的二阶方法难以精确提取轮廓 。作者引入了三阶差分来进一步增强细微的梯度变化和精细结构,通过强调更深层次的信号变化,提高了在低对比度红外图像中的轮廓清晰度和检测稳健性 。
问题2:从差分方程如何转换到本文的神经网络结构的?
TDE-Rev 的设计灵感来源于数值分析中求解常微分方程(ODE)的离散化方法 ,文中没有提,默认大家知道。简单来说,作者是通过数值分析中的有限差分法,把一个连续的微分方程变成了计算机可以计算的加减法。首先,作者给出了二阶导数在离散点 iii 处的标准近似公式 :
(∂2w∂x2)i≈wi+1−2wi+wi−1(Δx)2\left(\frac{\partial^{2}w}{\partial x^{2}}\right){i} \approx \frac{w{i+1}-2w_{i}+w_{i-1}}{(\Delta x)^{2}}(∂x2∂2w)i≈(Δx)2wi+1−2wi+wi−1
这里插播一下二阶差分是二阶导数的关系
二阶差分是二阶导数在离散空间下的近似实现。
二阶导数(Second Derivative) :属于微积分 范畴,定义在连续 函数上 。它描述的是函数变化率的变化率(即曲率),公式表达为 f′′(x)=limh→0f(x+h)−2f(x)+f(x−h)h2f''(x) = \lim_{h \to 0} \frac{f(x+h) - 2f(x) + f(x-h)}{h^2}f′′(x)=limh→0h2f(x+h)−2f(x)+f(x−h)。
二阶差分(Second Difference) :属于离散数学 范畴,定义在离散的序列或像素点上 。由于数字图像是由一个个孤立的像素点组成的,无法进行极限运算,因此使用差分来代替导数 。
论文中明确提到,为了在网络中处理图像特征,需要对二阶微分方程(SDE)进行"离散化" 。
它们通过泰勒级数展开 联系在一起。二阶差分的公式正是二阶导数去掉极限符号后的形式 ,当我们处理数字图像(特征图 www)时,像素点 iii 与 i+1i+1i+1 之间的距离是固定的,不能无限缩小。因此,作者采用了有限差分法 ,直接把极限符号扔掉,并将间隔 hhh 替换为离散的步长 Δx\Delta xΔx :
二阶差分≈wi+1−2wi+wi−1(Δx)2\text{二阶差分} \approx \frac{w_{i+1} - 2w_i + w_{i-1}}{(\Delta x)^2}二阶差分≈(Δx)2wi+1−2wi+wi−1
这就是论文中的公式 (14) 。
"去掉极限符号"不仅是数学上的简化,更是算法实现的前提:在红外图像中,最小的单位就是 1 个像素,所以 Δx=1\Delta x = 1Δx=1 。虽然去掉了极限,但分子部分 wi+1−2wi+wi−1w_{i+1} - 2w_i + w_{i-1}wi+1−2wi+wi−1 的结构 完全保留了二阶导数捕获"强度突变"的能力 。通过这种"去掉极限"的形式,作者才能进一步将公式变形为神经网络的残差连接 (即 wi+1=wi+Δwi+l(wi)w_{i+1} = w_i + \Delta w_i + l(w_i)wi+1=wi+Δwi+l(wi)),从而让网络在处理离散特征时,依然能执行类似高阶微分的操作 。
这里,wi+1w_{i+1}wi+1 是我们要预测的下一层状态,wiw_{i}wi 是当前层,wi−1w_{i-1}wi−1 是上一层。为了让公式看起来更像神经网络里的"残差连接",作者定义了两个差分项 :
Δwi+1=wi+1−wi\Delta w_{i+1} = w_{i+1} - w_{i}Δwi+1=wi+1−wi :表示从当前层到下一层的"增量"。
Δwi=wi−wi−1\Delta w_{i} = w_{i} - w_{i-1}Δwi=wi−wi−1 :表示从上一层到当前层的"增量"。
将这两个定义代入到第一步的分子中:wi+1−2wi+wi−1=(wi+1−wi)−(wi−wi−1)=Δwi+1−Δwiw_{i+1}-2w_{i}+w_{i-1} = (w_{i+1}-w_{i}) - (w_{i}-w_{i-1}) = \Delta w_{i+1} - \Delta w_{i}wi+1−2wi+wi−1=(wi+1−wi)−(wi−wi−1)=Δwi+1−Δwi
所以,原始的微分方程可以改写为:(Δx)2(∂2w∂x2)i=Δwi+1−Δwi(\Delta x)^{2} \left(\frac{\partial^{2}w}{\partial x^{2}}\right){i} = \Delta w{i+1} - \Delta w_{i}(Δx)2(∂x2∂2w)i=Δwi+1−Δwi
在神经网络中,通常用一个函数 l(wi)l(w_i)l(wi) 来学习(拟合)微分项。令 d=Δxd = \Delta xd=Δx,并将学习目标设为 l(wi)l(w_i)l(wi),公式变为 :Δwi+1=Δwi+d2l(wi)\Delta w_{i+1} = \Delta w_{i} + d^2 l(w_{i})Δwi+1=Δwi+d2l(wi),为了求出最终的 wi+1w_{i+1}wi+1,我们把 Δwi+1\Delta w_{i+1}Δwi+1 展开 :
wi+1−wi=Δwi+d2l(wi)w_{i+1} - w_{i} = \Delta w_{i} + d^2 l(w_{i})wi+1−wi=Δwi+d2l(wi)
wi+1=wi+Δwi+d2l(wi)w_{i+1} = w_{i} + \Delta w_{i} + d^2 l(w_{i})wi+1=wi+Δwi+d2l(wi)
当简化 d=1d=1d=1 时(对于数字图像,最小单位就是相邻的1个像素),就得到了论文中的最终残差形式 :
wi+1=wi+Δwi+l(wi)w_{i+1} = w_{i} + \Delta w_{i} + l(w_{i})wi+1=wi+Δwi+l(wi)
可能你会问为什么要这么变?我们回顾一下普通的残差结构(ResNet)中是wi+1=wi+l(wi)w_{i+1} = w_{i} + l(w_{i})wi+1=wi+l(wi)。它只看当前层,像是一阶马尔可夫链。而TDE-Rev 的残差结构是wi+1=wi+Δwi+l(wi)w_{i+1} = w_{i} + \mathbf{\Delta w_{i}} + l(w_{i})wi+1=wi+Δwi+l(wi),这里的 Δwi\Delta w_{i}Δwi 就像物理学里的"惯性"或者数学里的"动量" 。它不仅考虑了当前的特征 wiw_iwi,还考虑了特征的变化趋势(即 wi−wi−1w_i - w_{i-1}wi−wi−1)。这种引入了历史变化趋势的设计,使得网络能够捕获更高阶的边缘梯度信息,从而更精准地勾勒出红外小目标的微弱轮廓 。
这个结构揭示了学习的本质逻辑 :网络不需要直接学习完整的边缘图 wi+1w_{i+1}wi+1,这样难度太大 。Δwi\Delta w_{i}Δwi 是已有的趋势,l(wi)l(w_{i})l(wi) 则是网络在当前点学到的修正量 或精细补充 。从数学角度看,函数 l(wi)l(w_{i})l(wi) 的输出被映射为差分方程中的导数部分 。在训练完成后,当你把特征图 wiw_{i}wi 输入给这个残差块,它的输出在数值上就等效于在该点处经过深度优化后的"二阶变化率" 。
用个开车类比一下wiw_{i}wi 是你当前的位置,Δwi\Delta w_{i}Δwi 是你当前的行驶速度(一阶变化),微分项 l(wi)l(w_{i})l(wi) 就是你根据路况(当前特征)踩油门或刹车的加速度 (二阶变化)。神经网络不再使用一个固定的"巡航控制"系统,而是学习出一个极其聪明的"AI驾驶员" l(wi)l(w_{i})l(wi)。它能通过观察图像,精确决定在什么地方该"加速"强化边缘,在什么地方该"减速"抑制噪声 。
问题3:在神经网络中,通常用一个函数 l(wi)l(w_i)l(wi) 来学习(拟合)微分项是为什么?
这个问题其实是从第二个问题中衍生出来的。理解这个问题的核心,在于看清传统数学公式的"死"与 神经网络模型的"活"之间的差异。在传统数字图像处理中,如果我们想求二阶导数(即边缘检测),通常会使用一个固定 的数学模板(算子),比如拉普拉斯算子 。这样不管图像是云层、海面还是山地,二阶导数的计算方式永远是固定的几个数字相加减 。而红外小目标的特征极度微弱,且背景噪声复杂 。固定的数学公式无法应对多变的现实环境 。函数 l(wi)l(w_i)l(wi)(在代码中是一个残差块)通过大量数据训练,能够自动"悟"出在特定红外场景下,什么样的"导数计算方式"能最好地勾勒出目标轮廓,同时又不放大噪声 。
论文中提到的 TDE-Rev 结构,本质上是将一个二阶常微分方程(SDE)映射到了神经网络里 。论文推导出的二阶差分方程是一个理想化的物理模型 。但在真实的红外场景中,目标的灰度变化趋势极其复杂,人类很难写出一个完美的数学公式来描述这个微分项。既然我们写不出完美的公式,就给网络一个具有强大拟合能力的残差块结构 ,让它根据 LEdgeL_{Edge}LEdge 损失函数去自动"拟合"出那个最理想的微分算子 。
在数值分析中,解微分方程需要知道"变化量"。数学公式告诉我们 wi+1w_{i+1}wi+1 应该等于当前值加上某个"增量" 。而这个增量的核心部分就是微分项 。l(wi)l(w_i)l(wi) 充当了方程中的变化驱动力 。我们不需要预先推导出极其复杂的物理模型,而是让神经网络作为一个"万能函数拟合器",去逼近这个复杂的微分过程 。残差块 l(wi)l(w_i)l(wi) 只需要学习当前预测与真实完美边缘之间的"那一丁点差距(残差)"。对于神经网络来说,学习"差值"比从零开始学习一个完整的特征图要容易得多,也稳定得多 。
论文强调了"三阶"和"高阶"导数对于精细轮廓的重要性 。如果全靠手写数学公式,三阶以上的微分项会变得异常复杂,且对图像中的每一个坏点(噪声)都极度敏感 。通过函数 l(wi)l(w_i)l(wi) 学习出的微分项,具有更好的鲁棒性 。它能利用深度网络的非线性表达能力(ReLU、BatchNorm 等),过滤掉那些无意义的微小波动,只保留真正属于目标的梯度跳变 。
3.实验
benchmark 数据集上,该模型在交并比(IoU)、检出率(Pd)以及误报率(Fa)等核心评价指标上均超越了现有的 SOTA 方法 。可视化结果清晰地显示,随着 TDE-Rev 模块的逐级处理,目标边缘从模糊破碎逐渐演变为清晰连贯 。值得注意的是,得益于 Mamba 架构的线性复杂度优势,WMRNet 在维持高精度的同时实现了极致的轻量化:其参数量仅为 9.76 M ,推理时间缩短至 0.010 秒,为未来在机载或星载嵌入式平台上的实时部署提供了坚实的理论与工程支撑 。
4.代码复现
论文未开源代码,个人实现供学习,不确保与原作思想一致,实现为可插拔模块,方便集成到自己项目中。
4.1 DWMamba模块
python
import torch
import torch.nn as nn
import torch.nn.functional as F
from einops import rearrange
class HaarDWT(nn.Module):
"""
Haar 2D 离散小波变换:将特征图无损分解为低频 (LL) 和高频 (LH+HL+HH) [cite: 254]
"""
def __init__(self, in_channels):
super().__init__()
# Haar 滤波器权重
kernel = torch.tensor([
[1, 1, 1, 1], # LL (近似子带)
[1, -1, 1, -1], # LH (水平细节)
[1, 1, -1, -1], # LV (垂直细节)
[1, -1, -1, 1] # LD (对角线细节)
]).float() / 2.0
self.register_buffer('filter', kernel.view(4, 1, 2, 2).repeat(in_channels, 1, 1, 1))
def forward(self, x):
# 频率分离:下采样 2 倍
out = F.conv2d(x, self.filter, stride=2, groups=x.shape[1])
out = rearrange(out, 'b (k c) h w -> b k c h w', k=4)
i_l = out[:, 0] # 低频 I_L
i_h = out[:, 1:].sum(dim=1) # 融合高频 I_H [cite: 187, 188]
return i_l, i_h
class DW_SSM_Core(nn.Module):
"""
带高频注入的选择性状态空间模型核心算子
"""
def __init__(self, d_model, d_state=16):
super().__init__()
self.d_state = d_state
self.dt_proj = nn.Linear(d_model, d_model)
self.x_proj = nn.Linear(d_model, d_state * 2 + d_model, bias=False)
self.A_log = nn.Parameter(torch.log(torch.arange(1, d_state + 1).float().repeat(d_model, 1)))
self.D = nn.Parameter(torch.ones(d_model))
def forward(self, i_l, i_h):
B, L, D = i_l.shape
A = -torch.exp(self.A_log.float())
# 选择性映射
x_dbl = self.x_proj(i_l)
dt, B_param, C_param = torch.split(x_dbl, [D, self.d_state, self.d_state], dim=-1)
dt = F.softplus(self.dt_proj(dt))
# 离散化与扫描更新
dA = torch.exp(torch.einsum('bld,dn->bldn', dt, A))
dB = torch.einsum('bld,bln->bldn', dt, B_param)
h = torch.zeros(B, D, self.d_state, device=i_l.device)
ys = []
for t in range(L):
# 状态方程集成:h(t) = dA*h + dB*I_L + I_H
h = dA[:, t] * h + dB[:, t] * i_l[:, t].unsqueeze(-1) + i_h[:, t].unsqueeze(-1)
y = torch.einsum('bdn,bn->bd', h, C_param[:, t])
ys.append(y)
return torch.stack(ys, dim=1) + i_l * self.D
class DWMambaBlock(nn.Module):
"""
可插拔的 DW-Mamba 模块,实现全向空间感知
"""
def __init__(self, dim, d_state=16):
super().__init__()
self.dim = dim
self.dwt = HaarDWT(dim)
# 四路扫描器:水平、垂直双向扫描
self.scans = nn.ModuleList([DW_SSM_Core(dim, d_state) for _ in range(4)])
self.out_proj = nn.Linear(dim, dim)
def forward(self, x):
B, C, H, W = x.shape
# 1. 小波频率分解
i_l, i_h = self.dwt(x)
h2, w2 = i_l.shape[2], i_l.shape[3]
# 2. 准备四路输入序列
l_h = rearrange(i_l, 'b c h w -> b (h w) c') # 水平序列
h_h = rearrange(i_h, 'b c h w -> b (h w) c')
l_v = rearrange(i_l.transpose(2, 3), 'b c w h -> b (w h) c') # 垂直序列
h_v = rearrange(i_h.transpose(2, 3), 'b c w h -> b (w h) c')
# 3. 执行并行扫描
y1 = self.scans[0](l_h, h_h) # 正向水平
y2 = self.scans[1](l_h.flip(1), h_h.flip(1)).flip(1) # 逆向水平
y3 = self.scans[2](l_v, h_v) # 正向垂直
y4 = self.scans[3](l_v.flip(1), h_v.flip(1)).flip(1) # 逆向垂直
# 4. 特征重组
y_h = rearrange(y1 + y2, 'b (h w) c -> b c h w', h=h2, w=w2)
y_v = rearrange(y3 + y4, 'b (w h) c -> b c h w', h=h2, w=w2).transpose(2, 3)
# 聚合输出并投影
out = rearrange(y_h + y_v, 'b c h w -> b (h w) c')
out = self.out_proj(out)
return rearrange(out, 'b (h w) c -> b c h w', h=h2, w=w2)
def test_dwmamba():
# 模拟输入参数
batch_size = 2
channels = 64
height, width = 128, 128
# 1. 初始化模块
model = DWMambaBlock(dim=channels, d_state=16)
input_tensor = torch.randn(batch_size, channels, height, width)
# 2. 前向传播
print(f"--- DW-Mamba 测试 ---")
print(f"输入尺寸: {input_tensor.shape}")
with torch.no_grad():
output = model(input_tensor)
# 3. 验证输出尺寸
# 注意:由于 DWT 包含下采样,输出分辨率应为输入的一半 [cite: 193, 246]
expected_h, expected_w = height // 2, width // 2
print(f"输出尺寸: {output.shape}")
assert output.shape == (batch_size, channels, expected_h, expected_w)
print(f"验证状态: 输出维度正确,成功集成高低频并完成抗混叠下采样。")
if __name__ == "__main__":
test_dwmamba()4.2 TDE-Rev 模块
python
import torch
import torch.nn as nn
class ResidualBlock(nn.Module):
"""
论文中提到的残差块 l 和 g,用于特征增强
"""
def __init__(self, channels):
super().__init__()
self.conv = nn.Sequential(
nn.Conv2d(channels, channels, kernel_size=3, padding=1, bias=False),
nn.BatchNorm2d(channels),
nn.ReLU(inplace=True),
nn.Conv2d(channels, channels, kernel_size=3, padding=1, bias=False),
nn.BatchNorm2d(channels)
)
self.relu = nn.ReLU(inplace=True)
def forward(self, x):
return self.relu(x + self.conv(x))
class TDERevBlock(nn.Module):
"""
三阶差分方程引导的可逆结构 (TDE-Rev) 模块
"""
def __init__(self, v_channels, w_channels):
super().__init__()
# 1. SDE 部分:残差块 l(w_i)
self.l = ResidualBlock(w_channels)
# 2. 可逆交互部分:残差块 g 和通道映射 h
self.g = nn.Sequential(
nn.Conv2d(v_channels, w_channels, kernel_size=1), # 确保通道匹配
ResidualBlock(w_channels)
)
self.h = nn.Sequential(
nn.Conv2d(w_channels, v_channels, kernel_size=1), # 1x1 conv 改变通道 [cite: 293]
nn.BatchNorm2d(v_channels),
nn.ReLU(inplace=True)
)
def forward(self, v_prev, w_curr, w_prev):
"""
v_prev: 分割流特征 (Seg Stream)
w_curr: 当前边缘流特征 (Edge Stream w_i)
w_prev: 前一阶段边缘流特征 (Edge Stream w_{i-1})
"""
# A. SDE 引导的边缘更新
# Delta w_i = w_i - w_{i-1}
delta_w = w_curr - w_prev
# w_temp = Delta w_i + w_i + l(w_curr) -> 即公式中的 w_{i+1}
w_sde = delta_w + w_curr + self.l(w_curr)
# B. 第一阶段可逆更新:w_{i+2} = w_{i+1} + g(v_{i+1}) [cite: 314]
w_next = w_sde + self.g(v_prev)
# C. 第二阶段可逆更新:v_{i+2} = v_{i+1} + h(w_{i+2}) [cite: 314]
v_next = v_prev + self.h(w_next)
return v_next, w_next
def test_tde_rev():
# 参数设置:假设分割流 64 通道,边缘流 32 通道
v_ch, w_ch = 64, 32
batch, h, w = 1, 128, 128
# 初始化模块
tde_rev = TDERevBlock(v_channels=v_ch, w_channels=w_ch)
# 模拟输入
v_stream = torch.randn(batch, v_ch, h, w) # 分割流输入
w_curr = torch.randn(batch, w_ch, h, w) # 边缘流当前态 (w_i)
w_prev = torch.randn(batch, w_ch, h, w) # 边缘流先前态 (w_{i-1})
print("--- TDE-Rev 模块测试 ---")
print(f"输入 Seg 尺寸: {v_stream.shape}")
print(f"输入 Edge (curr) 尺寸: {w_curr.shape}")
# 执行计算
v_out, w_out = tde_rev(v_stream, w_curr, w_prev)
print(f"输出 Seg 尺寸: {v_out.shape}")
print(f"输出 Edge 尺寸: {w_out.shape}")
# 验证逻辑
assert v_out.shape == v_stream.shape
assert w_out.shape == w_curr.shape
print("验证状态: 输出维度一致,二阶差分项与可逆交互计算完成。")
if __name__ == "__main__":
test_tde_rev()