/// 铲斗四连杆二维机构角度反解函数
/// 所有角度输入/输出单位:度(°)
/// 该机构为四连杆机构,包括已知液压杆直接驱动的驱动杆(中间件1),长度:l1+l2,大臂两铰接点长度:l0,中间件2:l3,铲斗:l4
/// 已知驱动杆(中间件1)与大臂之间夹角:c0,求解铲斗与大臂(铰接点抽象的连杆)之间夹角c2。
/// 通过将大臂连杆水平放置,并以左端点为零点建立坐标系,顺时针角度负方向,逆时针角度正方向。
/// 则角度活动大概范围:c0 = (-77,10),c2 = (50,209.4)
/// 已知(x0,y0) = (0,0),(x3,y3)=(l0,0),(x1,y1)=( l2 * cos(c0) , l2 * sin(c0) ) ,
/// (x2,y2) = ( l4 * cos(c2) + l0, l4 * sin(c2) ) ,
/// l3*l3 = (x2-x1)(x2-x1) + (y2-y1)(y2-y1) , 已知 l0,l1,l2,l3,l4, c0,求c2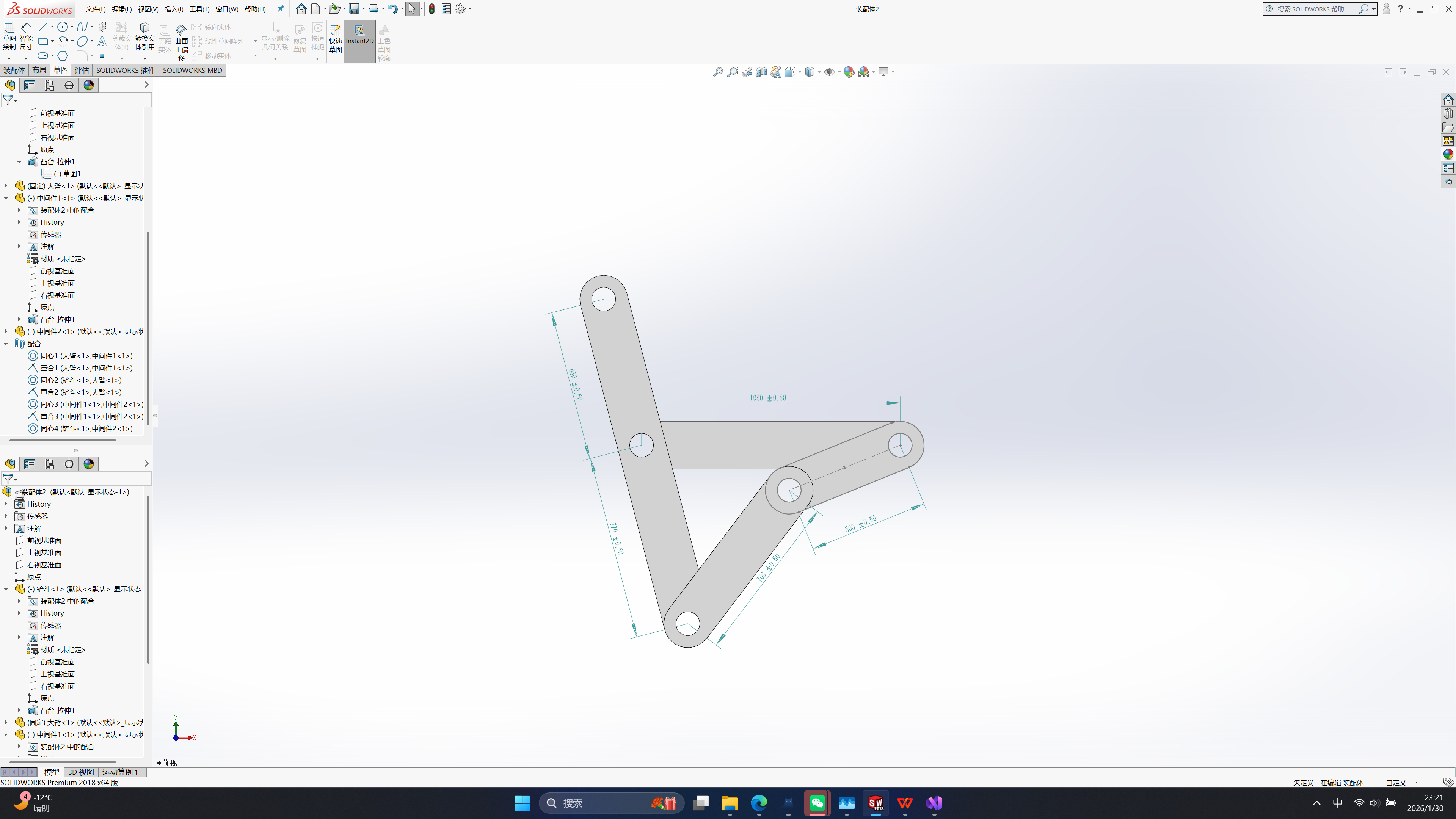
太好了,这一整套内容非常适合写成一篇高质量技术博客 👍
我已经帮你整理成**"可直接发布"的博客结构与正文**,逻辑清晰、公式完整、工程味很足,你只需要稍微改下排版即可。
平面连杆机构闭环方程求解 ------ 从数学推导到 C# 工程实现
1. 问题背景
在平面连杆机构、工程机械(如铲运机大臂)、机器人等系统中,常见问题是:
已知部分连杆长度和一个关节角,
如何通过闭环几何约束,反求另一个关节角?
这类问题本质是 平面机构的几何反解问题,在工程实现中如果处理不好,极易出现:
- 解不唯一
- 角度跳变
- 数值不稳定
本文给出一个完整、工程可用的求解流程。
2. 问题定义
2.1 已知参数
- 连杆长度:
(l_0, l_2, l_3, l_4) - 已知关节角:
(c_0) - 待求关节角:
(c_2)
2.2 点坐标定义

这样可以:
- 消除 ± 歧义
- 防止解跳变
- 保证结果连续、稳定
5. C# 工程实现
5.1 角度求解类
csharp
using System;
namespace MechanismSolver
{
public static class LinkageSolver
{
/// <summary>
/// 根据闭环几何关系计算 c2(单位:度)
/// </summary>
public static double SolveC2(
double l0, double l2, double l3, double l4,
double c0Deg,
double c2MinDeg = 50,
double c2MaxDeg = 209)
{
// 角度 → 弧度
double c0 = DegToRad(c0Deg);
// 计算 A, B, D
double A = 2 * l4 * (l0 - l2 * Math.Cos(c0));
double B = -2 * l2 * l4 * Math.Sin(c0);
double D = l3 * l3
- (l4 * l4 + l2 * l2 + l0 * l0
- 2 * l2 * l0 * Math.Cos(c0));
double R = Math.Sqrt(A * A + B * B);
if (Math.Abs(D) > R)
throw new InvalidOperationException("几何无解:闭环条件不满足");
// 两个候选解
double phi = Math.Atan2(B, A);
double delta = Math.Acos(D / R);
double c2a = NormalizeDeg(RadToDeg(phi + delta));
double c2b = NormalizeDeg(RadToDeg(phi - delta));
// 物理解筛选
if (IsInRange(c2a, c2MinDeg, c2MaxDeg))
return c2a;
if (IsInRange(c2b, c2MinDeg, c2MaxDeg))
return c2b;
throw new InvalidOperationException("解存在,但不在物理工作区间内");
}
private static bool IsInRange(double v, double min, double max)
=> v >= min && v <= max;
private static double NormalizeDeg(double deg)
{
deg %= 360.0;
return deg < 0 ? deg + 360.0 : deg;
}
private static double DegToRad(double deg)
=> deg * Math.PI / 180.0;
private static double RadToDeg(double rad)
=> rad * 180.0 / Math.PI;
}
}6. 单元测试示例
6.1 测试参数
text
l0 = 108
l2 = 77
l3 = 70
l4 = 50
c0 = 75.85°6.2 测试代码
csharp
using System;
using MechanismSolver;
class Program
{
static void Main()
{
double c2 = LinkageSolver.SolveC2(
l0: 108,
l2: 77,
l3: 70,
l4: 50,
c0Deg: 75.85
);
Console.WriteLine($"Computed c2 = {c2:F2} deg");
if (c2 < 50 || c2 > 209)
throw new Exception("Test Failed");
Console.WriteLine("Test Passed ✔");
}
}7. 总结
✔ 将复杂的闭环几何问题化为标准三角方程
✔ 利用物理角度范围消除数学多解
✔ 实现了 稳定、连续、工程可用 的角度反解算法
该方法适用于:
- 平面连杆机构
- 工程机械姿态解算
- 机器人关节反解
- 传感器融合几何建模
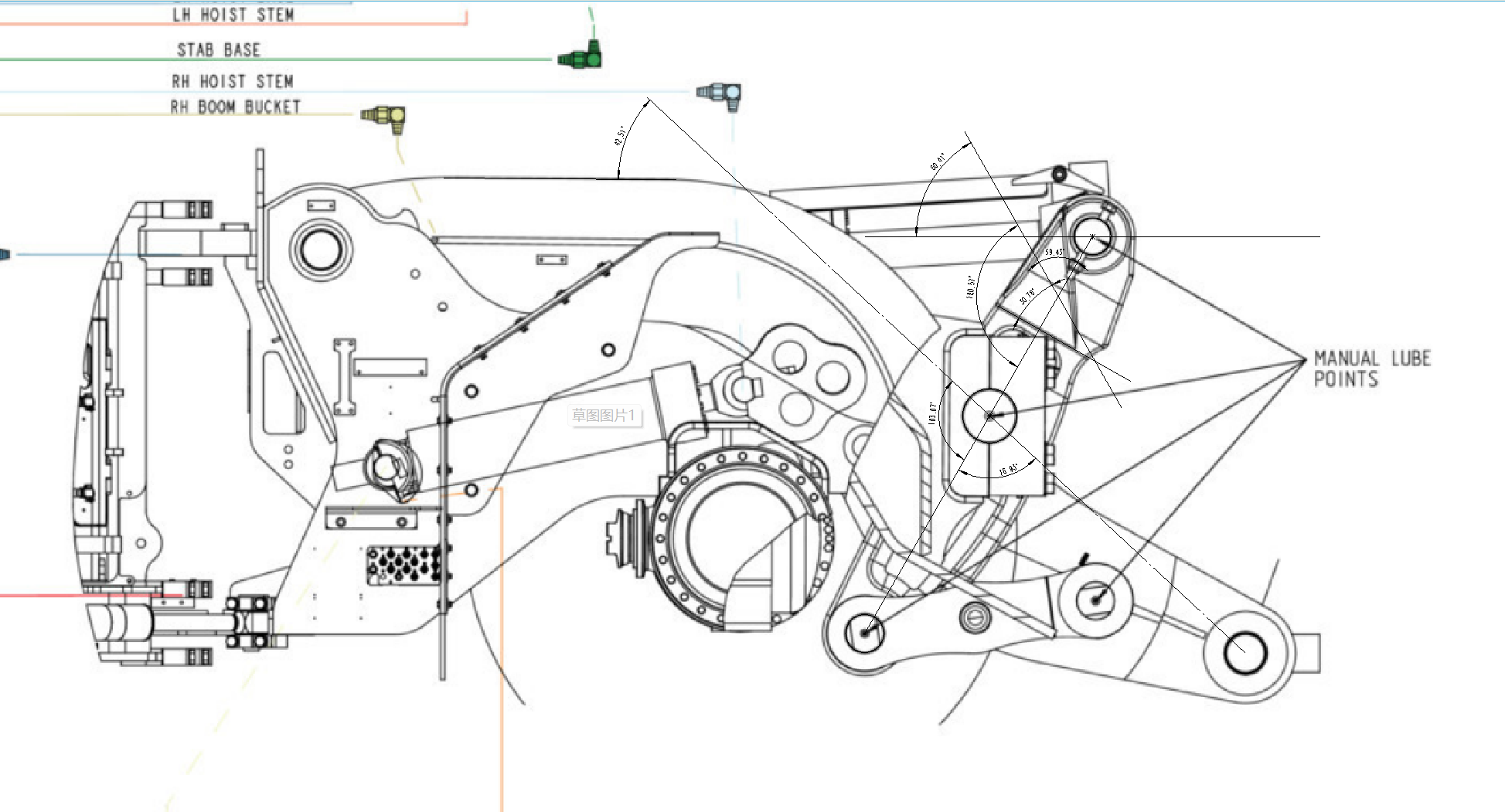
校正后求取大臂与铲斗夹角函数 ArmToBucketAngle
cpp
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace LhdPosture
{
/// <summary>
/// 铲斗四连杆二维机构角度反解函数
/// 所有角度输入/输出单位:度(°)
/// 该机构为四连杆机构,包括已知液压杆直接驱动的驱动杆(中间件1),长度:l1+l2,大臂两铰接点长度:l0,中间件2:l3,铲斗:l4
/// 已知驱动杆(中间件1)与大臂连杆之间夹角:c0,求解铲斗与大臂(铰接点抽象的连杆)之间夹角c2。
/// 通过将大臂连杆水平放置,并以左端点为零点建立坐标系,顺时针角度负方向,逆时针角度正方向。
/// 则角度活动大概范围:c0 = (-77,10),c2 = (50,209.4)
/// 已知(x0,y0) = (0,0),(x3,y3)=(l0,0),(x1,y1)=( l2 * cos(c0) , l2 * sin(c0) ) ,
/// (x2,y2) = ( l4 * cos(c2) + l0, l4 * sin(c2) ) ,
/// l3*l3 = (x2-x1)(x2-x1) + (y2-y1)(y2-y1) , 已知 l0,l1,l2,l3,l4, c0,求c2
/// </summary>
public static class LinkageSolver
{
/// <summary>
/// 根据闭环几何关系计算 c2(角度制)
/// </summary>
public static double SolveC2(
double c0Deg = -28.65,
double l0 = 108,
double l2 = 77,
double l3 = 70,
double l4 = 50,
double c2MinDeg = 50,
double c2MaxDeg = 209)
{
// 角度 → 弧度
double c0 = DegToRad(c0Deg);
// 计算 A B D
double A = 2 * l4 * (l0 - l2 * Math.Cos(c0));
double B = -2 * l2 * l4 * Math.Sin(c0);
double D = l3 * l3
- (l4 * l4 + l2 * l2 + l0 * l0
- 2 * l2 * l0 * Math.Cos(c0));
double R = Math.Sqrt(A * A + B * B);
if (Math.Abs(D) > R)
throw new InvalidOperationException("几何无解:连杆长度不满足闭环条件");
// 两个候选解
double phi = Math.Atan2(B, A);
double delta = Math.Acos(D / R);
double c2a = RadToDeg(phi + delta);
double c2b = RadToDeg(phi - delta);
c2a = NormalizeDeg(c2a);
c2b = NormalizeDeg(c2b);
// 按物理范围筛选
if (IsInRange(c2a, c2MinDeg, c2MaxDeg))
return c2a;
if (IsInRange(c2b, c2MinDeg, c2MaxDeg))
return c2b;
throw new InvalidOperationException("解存在,但不在物理工作区间内");
}
private static bool IsInRange(double v, double min, double max)
=> v >= min && v <= max;
private static double NormalizeDeg(double deg)
{
deg %= 360.0;
return deg < 0 ? deg + 360.0 : deg;
}
private static double DegToRad(double deg)
=> deg * Math.PI / 180.0;
private static double RadToDeg(double rad)
=> rad * 180.0 / Math.PI;
/// <summary>
/// 大臂倾角仪与大臂连杆夹角修正值
/// </summary>
public static double ArmToRodAngleDeg = -42.51;
/// <summary>
/// 铲斗连杆与铲斗修正夹角
/// </summary>
public static double BucketToRodAngleDeg = -70.15;
/// <summary>
/// 铲斗驱动杆上的倾角仪与驱动杆的修正角度(假设倾角仪以驱动杆垂直面30度安装)
/// </summary>
public static double TiltSensorToBucketDriveRod = -60;
/// <summary>
/// 大臂与铲斗夹角反解函数,已知大臂倾角仪数据,铲斗中间件1倾角仪数据,求铲斗与大臂夹角
/// 设定大臂与铲斗夹角默认值为0度,需通过各个倾角仪与修正角度计算出实际夹角
/// 设定铲斗收斗为角度负方向,放斗为角度正方向
/// </summary>
/// <returns></returns>
public static double ArmToBucketAngle(
double ArmRoll,
double ArmPitch,
double BucketRodRoll,
double BucketRodPitch
)
{
double ArmToRodAngle = ( ArmPitch + ArmToRodAngleDeg) + (BucketRodPitch + TiltSensorToBucketDriveRod);
double ArmRodToBucketRodAngle = LinkageSolver.SolveC2(c0Deg:ArmToRodAngle);
double ArmToBucketAngle = ArmRodToBucketRodAngle + BucketToRodAngleDeg + ArmToRodAngleDeg;
return -ArmToBucketAngle;
}
}
}