信号处理入门4（系统设计）

这部分主要是如何改变信号，涉及到的内容主要是FIR滤波器、IIR滤波器、稳定性相关。之前在数学工具那一篇说过，差分方程分为不带反馈的和带反馈的，于是不带反馈的就是FIR，带反馈的就是IIR。

这部分滤波器，可以软件实现也可以硬件实现，一般来说简单的可以直接用模拟电路解决，复杂的还是用DSP/FPGA或者自己用上层软件解决。

1 FIR滤波器

FIR滤波器 (Finite Impulse Response)，有限冲激响应滤波器。简单一点说就是 "加权平均值"。它只关心现在和过去有限时间段内的数据。拿一个固定长度的滑块（窗口），对窗口内的数据进行加权求和。为了达到好的过滤效果，通常需要很长的"窗口"，计算量相对较大。

数学表达式：

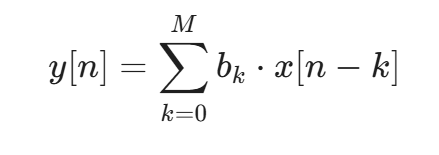
FIR滤波器可以平滑输出，这个只是基本应用，主要的还是信号的重塑，分频，监测。

1.1 信号的重塑

以回音为例，假设原始声音信号是 x[n]。由于环境反射，收到的实际信号 y[n]包含了原声和一个延迟了3个单位、强度减半的回声。

怎么用FIR消除这个回音呢？

此时就可以设计一个FIR滤波器，它的逻辑是用当前的信号，减去0.5倍的过去三个单位的信号。回音的方程就是y[n] = x[n]+0.5 * x[n-3]。

这样新的信号中，回音就因为制造的信号相干抵消 (Destructive Interference)被干掉了。

1.2 信号的分频

信号有低频和高频。低频的特点就是波动非常平滑、缓慢，波峰和波谷之间隔得很远。比如大鼓声、大提琴、或是远处隆隆的雷声。从数学上看就是相邻的两个点数值很接近。高频则是波动极其剧烈、短促。波峰和波谷紧挨在一起，像被密集的锯齿。比如哨声、小提琴的高音、或是收音机里的"滋滋"静电声。从数学上看就是相邻的采样点之间数值跳动极大，甚至直接从大的正值跳到大的负值。

所以对于低频的低通滤波器就是平滑，做加权平均，直接把跳动的部分抵消掉。而高频的高通滤波器就是1,-1的正负交替，这样可以把变化更强烈的输出。

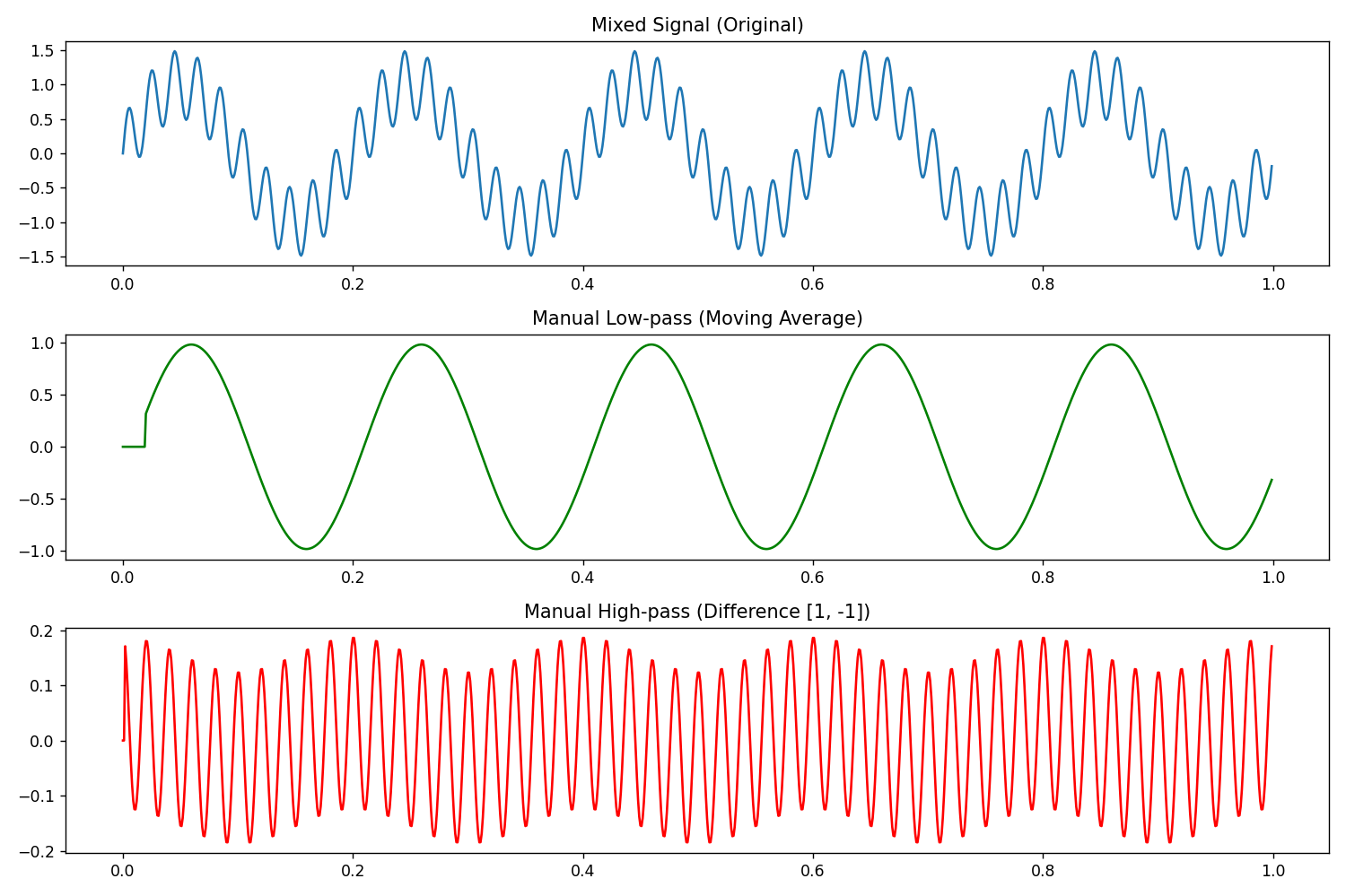
Pyhton模拟5Hz的低频+50Hz的高频。这里低通滑动窗口用的20，也就是20个参数。高通只有2个参数。

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

# 1. 准备数据
fs = 1000  # 采样率 1000Hz
t = np.linspace(0, 1, fs, endpoint=False)

# 生成混合信号：5Hz趋势 + 50Hz抖动
low_freq = np.sin(2 * np.pi * 5 * t)
high_freq = 0.5 * np.sin(2 * np.pi * 50 * t)
mixed_signal = low_freq + high_freq

# 2. 手动设计 FIR 系数 (Manual FIR Coefficients)

# --- 低通：简单移动平均 (Moving Average) ---
# 就像是一个滑动的窗口，取 20 个点的平均值
order_lp = 20
coeffs_lp = np.ones(order_lp) / order_lp  # 所有系数都是正的 0.05

# --- 高通：简单的差分 (Simple Difference) ---
# 比较相邻两个点的差异：[1, -1]
coeffs_hp = np.array([1, -1])

# 3. 手动执行差分方程 (Manual Convolution)
# 在硬件里，这通常是一个 for 循环
def manual_fir(data, coeffs):
    n = len(data)
    m = len(coeffs)
    output = np.zeros(n)
    # 核心算法：y[n] = b0*x[n] + b1*x[n-1] + ...
    for i in range(m, n):
        # 这一行就是 FIR 的差分方程本质：乘累加 (MAC)
        output[i] = np.sum(data[i-m+1 : i+1] * coeffs[::-1])
    return output

# 执行滤波
filtered_low = manual_fir(mixed_signal, coeffs_lp)
filtered_high = manual_fir(mixed_signal, coeffs_hp)

# 4. 绘图
plt.figure(figsize=(12, 8))

plt.subplot(3, 1, 1)
plt.plot(t, mixed_signal)
plt.title("Mixed Signal (Original)")

plt.subplot(3, 1, 2)
plt.plot(t, filtered_low, color='green')
plt.title("Manual Low-pass (Moving Average)")

plt.subplot(3, 1, 3)
plt.plot(t, filtered_high, color='red')
plt.title("Manual High-pass (Difference [1, -1])")

plt.tight_layout()
plt.show()

结果：

1.3 信号的监测

其实就是之前说的自相关判断，两个信号的点积。然后在这里不停的滑动做，于是就叫做-----卷积（convolution）。卷积和相关（Correlation）的区别就是要不要翻转。我目前还不是很明白为什么卷积要翻转，后面继续学习吧TODO。

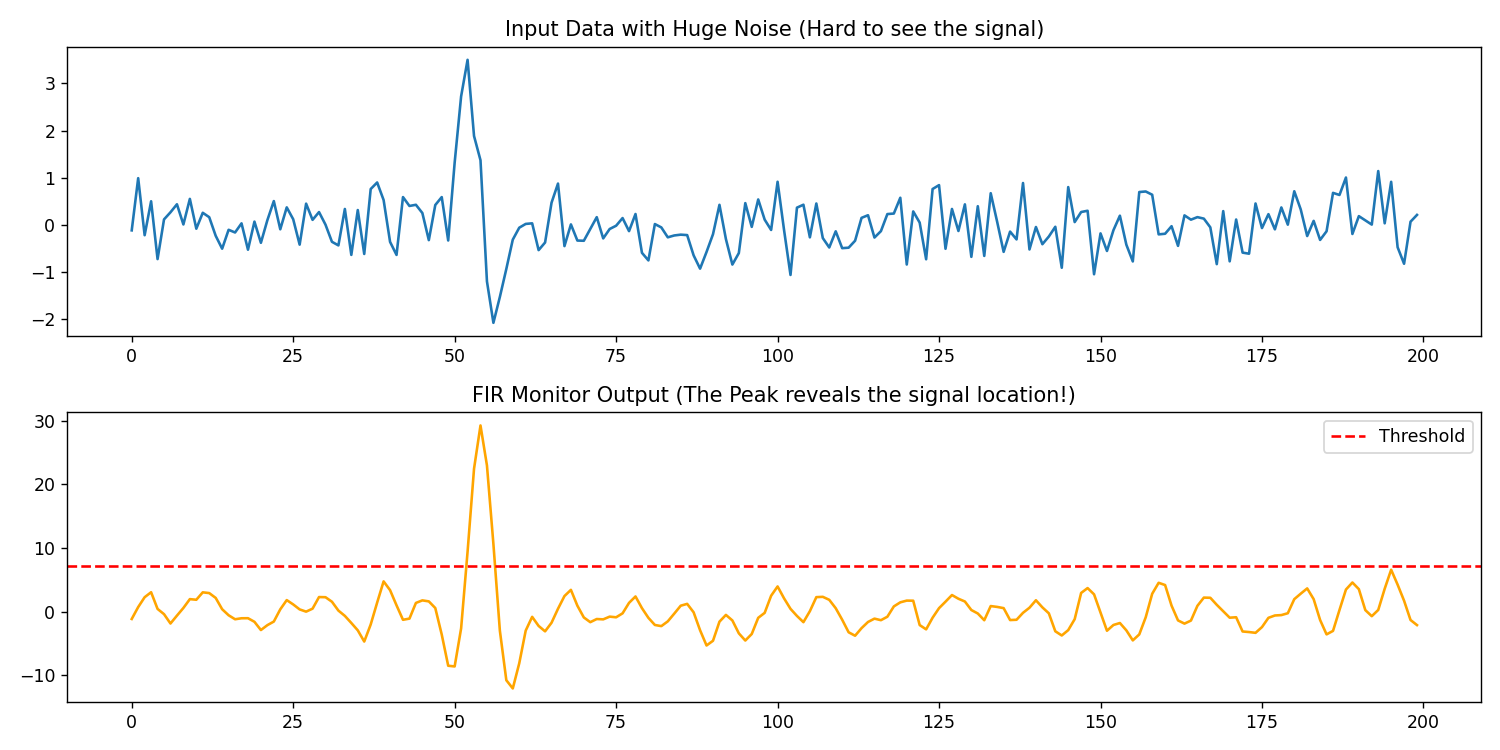
下面一个具体的例子，看看一段信号中，有没有出现[1, 2, 3, 2, 1, -1, -2, -1]这个信号。这种应用可以用在判断声纳，雷达回波等很多场景。

代码：

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

# 1. 定义我们想要找的"目标模式" (比如一个特定的脉冲)
template = np.array([1, 2, 3, 2, 1, -1, -2, -1])

# 2. 生成一段很长的背景噪声，并把目标藏在中间
noise = np.random.normal(0, 0.5, 200) # 强噪声
signal_stream = np.concatenate([np.zeros(50), template, np.zeros(142)])
input_data = signal_stream + noise # 此时肉眼几乎看不见目标

# 3. 设计监测 FIR 滤波器 (匹配滤波器)
# 系数就是目标的倒影
coeffs_monitor = template[::-1]

# 4. 执行卷积运算 (监测过程)
output = np.convolve(input_data, coeffs_monitor, mode='same')

# 5. 绘图
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(input_data)
plt.title("Input Data with Huge Noise (Hard to see the signal)")

plt.subplot(2, 1, 2)
plt.plot(output, color='orange')
plt.axhline(y=np.max(template**2)*0.8, color='r', linestyle='--', label='Threshold')
plt.title("FIR Monitor Output (The Peak reveals the signal location!)")
plt.legend()
plt.tight_layout()
plt.show()

结果，可以看到，整个信号的强度放大了差不多10倍。

2 IIR滤波器

IIR 滤波器 (Infinite Impulse Response)，无限冲激响应滤波器。形象理解： "带有记忆的反馈"。它不仅看现在的输入，还看上一时刻自己输出的结果。它通过递归的方式，把一部分输出反馈回来重新参与计算。只需很少的计算（阶数很低）就能达到极强的过滤效果。但是如果参数没调好，它可能会像麦克风靠近音箱一样产生自激震荡（数值无限增大）。其实这个就是在上一篇所说的带反馈的差分方程。

绝大部分的硬件滤波，都是属于IIR。一个电容的RC低通滤波器，数学上就是一个典型的一阶IIR滤波器。

数学表达式：

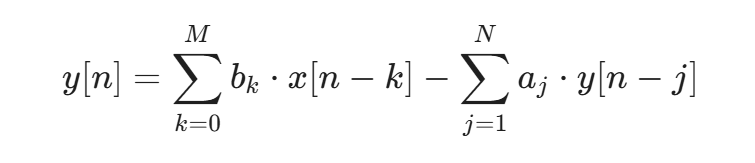
IIR相对于FIR，存在低计算量、高陡峭度的特点，也就是算力更少效果更大。更少的参数就可以实现FIR的效果。完成同样的滤波，IIR 可能只需要 5 阶（5 个系数）。FIR 可能需要 500 阶（500 个系数）。但是IIR这种递归存在风险，参数一旦有小偏差，随着时间累计误差可能就会爆。。。

功能上IIR能做的，FIR也完全能做。所以就不一一举例了。因为IIR运算量小的多，所以实时性要求更高，比如实时音频、传感器监控等，或者在资源受限的系统，比如MCU，IIR就用的更多。IIR除了稳定性还有一个问题是可能存在相位扭曲。所以对时间精度要求非常高的场合，比如图像处理、高保真音响（Hi-Fi）、精密测量，这些场合就要用IIR。

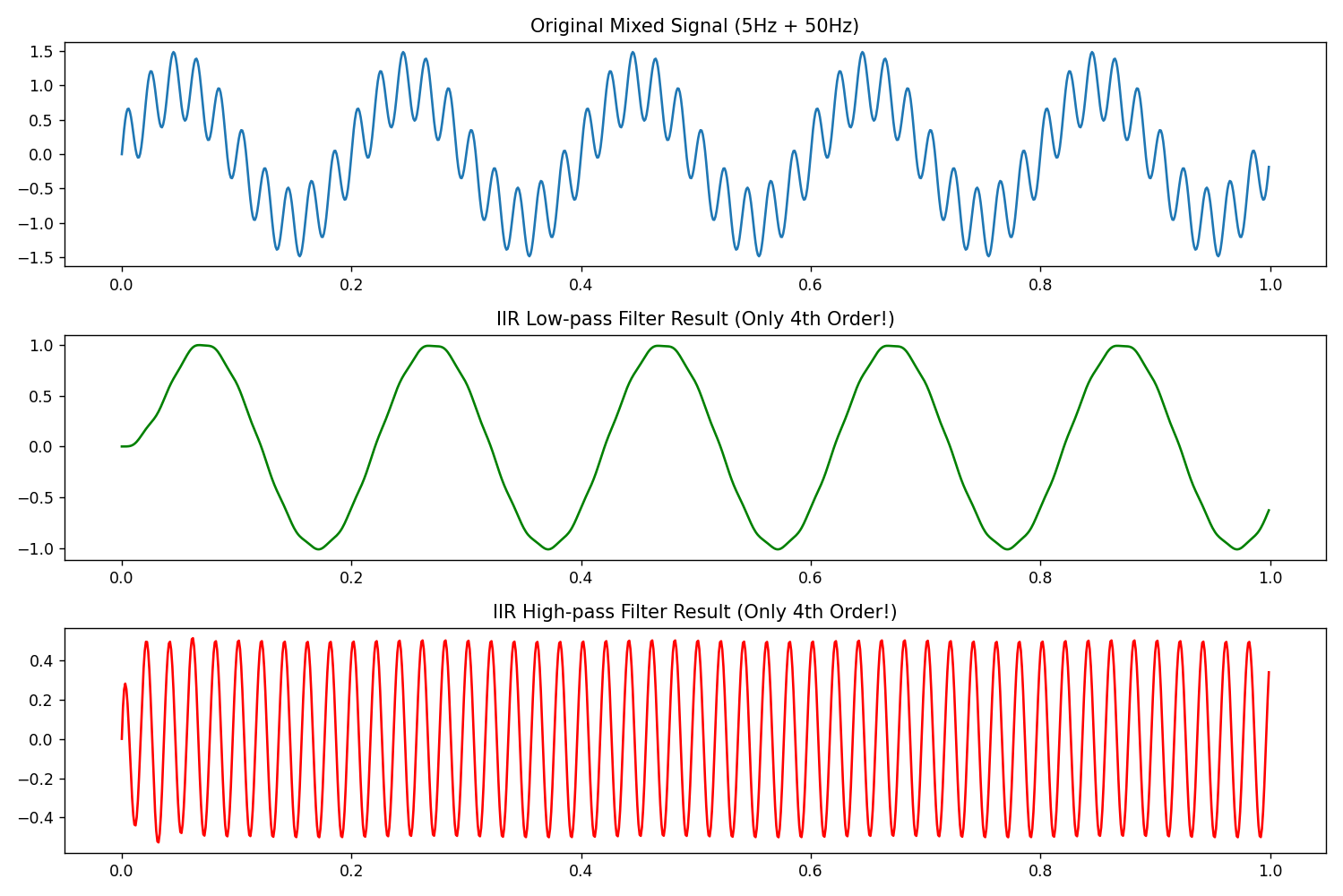
这里给一个示例，还是上面的分频。用的是巴特沃斯滤波器 (Butterworth Filter)，这里只用了4阶，也就是4个参数。

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 1. 准备数据
fs = 1000  # 采样率 1000Hz
t = np.linspace(0, 1, fs, endpoint=False)

# 生成信号：5Hz 低频 + 50Hz 高频
low_freq_signal = np.sin(2 * np.pi * 5 * t)
high_freq_signal = 0.5 * np.sin(2 * np.pi * 50 * t)
mixed_signal = low_freq_signal + high_freq_signal

# 2. 设计 IIR 低通滤波器 (只保留 5Hz)
# N=4 表示 4 阶，Wn=20 是截止频率
# b 是前馈系数 (分子), a 是反馈系数 (分母)
b_lp, a_lp = signal.butter(N=4, Wn=20, btype='low', fs=fs)
filtered_low_iir = signal.lfilter(b_lp, a_lp, mixed_signal)

# 3. 设计 IIR 高通滤波器 (只保留 50Hz)
b_hp, a_hp = signal.butter(N=4, Wn=20, btype='high', fs=fs)
filtered_high_iir = signal.lfilter(b_hp, a_hp, mixed_signal)

# 4. 观察 IIR 的"精简"系数
print("IIR Low-pass b coeffs (Forward):", b_lp)
print("IIR Low-pass a coeffs (Feedback):", a_lp)
print(f"Total coeffs used: {len(b_lp) + len(a_lp)}") # 总共才 10 个左右

# 5. 绘图
plt.figure(figsize=(12, 8))

plt.subplot(3, 1, 1)
plt.plot(t, mixed_signal)
plt.title("Original Mixed Signal (5Hz + 50Hz)")

plt.subplot(3, 1, 2)
plt.plot(t, filtered_low_iir, color='green')
plt.title("IIR Low-pass Filter Result (Only 4th Order!)")

plt.subplot(3, 1, 3)
plt.plot(t, filtered_high_iir, color='red')
plt.title("IIR High-pass Filter Result (Only 4th Order!)")

plt.tight_layout()
plt.show()

结果：

3 稳定性

稳定性的监测，主要就是针对上面的IIR滤波器。上面也说了，IIR的递归存在风险，参数一旦产生有小偏差，随着时间累计误差放大可能就会爆。这个也不打算现在太深入去研究，先简单总结一下吧。

A. 设计层面的监测（极点检查）

在代码写好之前，会用数学工具（如 Python 的 scipy.signal.tf2zpk）检查极点。单位圆准则：如果极点的模（到原点的距离）大于或等于 1，这个滤波器在理论上就是不稳定的。监测点：极点距离单位圆边缘有多近？如果太近（例如 0.99），虽然理论稳定，但在实际运行中极易受干扰。

B. 运行层面的监测（溢出处理）

在硬件（如 DSP 芯片）实时跑IIR时，系统会监测：寄存器溢出：由于反馈的存在，如果y[n]开始变得异常大，它会作为下一次的输入进一步推高结果。极限环震荡（Limit Cycle）：在输入信号消失后，由于舍入误差，IIR 可能会在几个很小的数值之间来回跳动，停不下来。

在现代实际应用中，为了防止 IIR 稳定性失控，很少直接用一个高阶IIR（比如 10 阶），而是把它拆成多个二阶滤波器（Second-Order Sections, SOS）串联。