lc3345
直接 +n) % n 会越界,要
++% n + n) % n]; // 保证结果在 [0,n-1] 中++
class Solution {
public:
vector<int> constructTransformedArray(vector<int>& nums) {
int n = nums.size();
vector<int> result(n);
for (int i = 0; i < n; i++) {
result[i] = nums[((i + nums[i]) ++% n + n) % n]; // 保证结果在 [0,n-1] 中++
}
return result;
}
};
lc3031
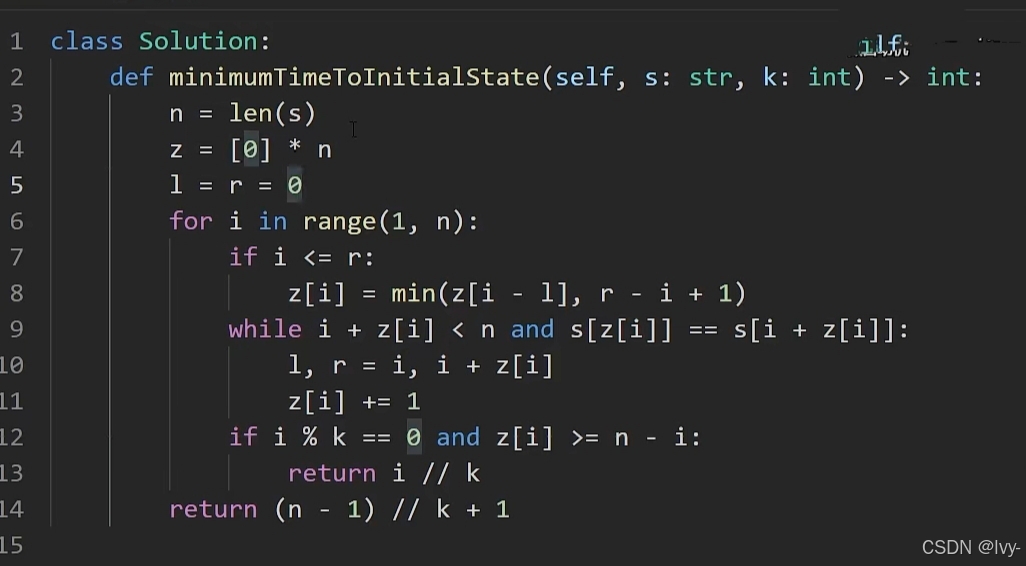
++Z 算法 求出字符串的最长前缀匹配++
找到第一个能被 k 整除且匹配完整后缀的位置,返回最少操作次数
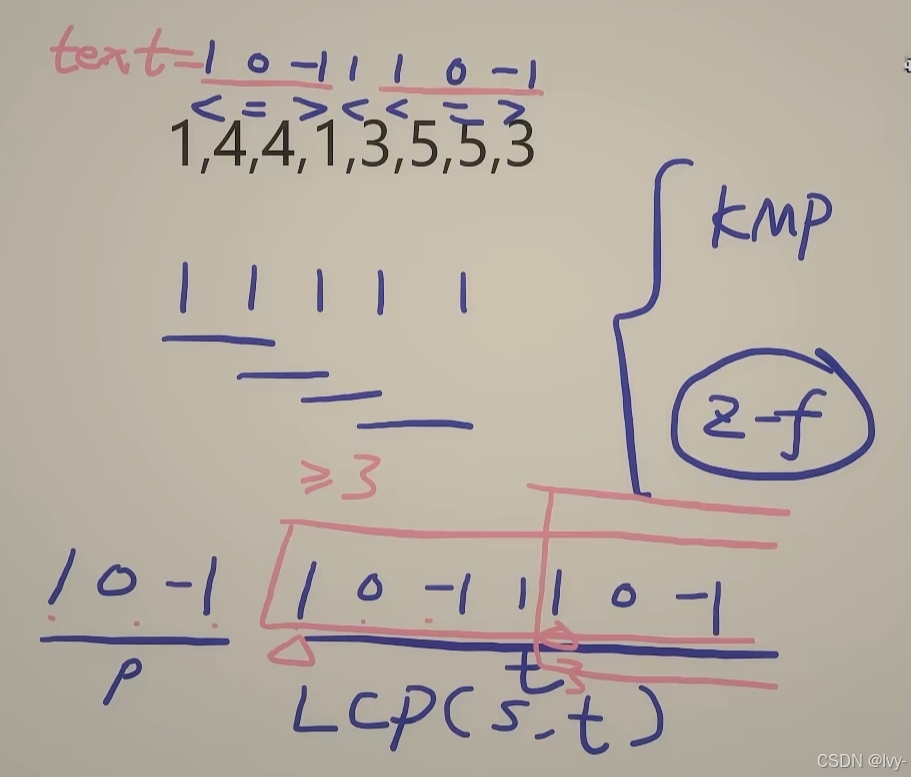
Z 算法就是快速找出字符串里,每个位置和开头的最长公共前缀长度
给字符串 s ,算出数组 Z , ++Z[i] 表示 s 从 i 开始++,和 s 开头最长匹配多长。
用一个++区间 [l, r] 记录当前最右的匹配区间, 避免重复比较++,做到线性时间 O(n)
遍历每个位置:
若在区间内,先继承已有结果;
再暴力往后比,更新区间;
最后得到完整 Z 数组。
sum:用区间复用结果,少做重复比较,快速拿到每个位置和开头的匹配长度

class Solution {
public:
int minimumTimeToInitialState(string s, int k) {
int n = s.size();
vector<int> z(n);
int l = 0, r = 0;
for (int i = 1; i < n; i++) {
if (i <= r)
z[i] = min(z[i - l], r - i + 1);
while (i + z[i] < n && s[z[i]] == s[i + z[i]]) {
l = i;
r = i + z[i];
z[i]++;
}
if (i % k == 0 && z[i] >= n - i) {
return i / k;
}
}
return (n - 1) / k + 1;
}
};