深度学习优化器详解：指数加权平均EWA、动量梯度下降Momentum、均方根传递RMSprop、Adam 从原理到实操

目录标题

• [深度学习优化器详解：EWA、Momentum、RMSprop、Adam 从原理到实操](#深度学习优化器详解：EWA、Momentum、RMSprop、Adam 从原理到实操)
• • 开篇铺垫：为什么需要这些优化算法？
  • [一、基础工具：指数加权平均（EWA）------ 所有优化器的"平滑基石"](#一、基础工具：指数加权平均（EWA）—— 所有优化器的“平滑基石”)
  • • [1.1 核心背景：为什么需要"平滑"？](#1.1 核心背景：为什么需要“平滑”？)
    • [1.2 原理拆解：EWA的核心逻辑（通俗版）](#1.2 原理拆解：EWA的核心逻辑（通俗版）)
    • [1.3 公式推导（严谨版，新手可跳过推导看结论）](#1.3 公式推导（严谨版，新手可跳过推导看结论）)
    • [1.4 关键细节： β \beta β的选择与有效窗口（实操重点）](#1.4 关键细节： β \beta β的选择与有效窗口（实操重点）)
    • [1.6 小结](#1.6 小结)
  • [二、第一代优化器：动量梯度下降（Momentum）------ 解决梯度震荡，加速收敛](#二、第一代优化器：动量梯度下降（Momentum）—— 解决梯度震荡，加速收敛)
  • • [2.1 核心背景：Momentum要解决的痛点](#2.1 核心背景：Momentum要解决的痛点)
    • [2.2 原理拆解：Momentum的核心逻辑](#2.2 原理拆解：Momentum的核心逻辑)
    • [2.3 公式推导](#2.3 公式推导)
    • [2.4 实操细节（避坑重点）](#2.4 实操细节（避坑重点）)
    • [2.6 小结](#2.6 小结)
  • [三、第二代优化器：RMSprop ------ 自适应学习率，解决更新步调不一致](#三、第二代优化器：RMSprop —— 自适应学习率，解决更新步调不一致)
  • • [3.1 核心背景：RMSprop要解决的痛点](#3.1 核心背景：RMSprop要解决的痛点)
    • [3.2 原理拆解：RMSprop的核心逻辑](#3.2 原理拆解：RMSprop的核心逻辑)
    • [3.3 公式推导（严谨版）](#3.3 公式推导（严谨版）)
    • [3.4 实操细节（避坑重点）](#3.4 实操细节（避坑重点）)
    • [3.6 小结](#3.6 小结)
  • [四、终极优化器：Adam ------ 融合Momentum与RMSprop，工业界标配](#四、终极优化器：Adam —— 融合Momentum与RMSprop，工业界标配)
  • • [4.1 核心背景：Adam要解决的痛点](#4.1 核心背景：Adam要解决的痛点)
    • [4.2 原理拆解：Adam的核心逻辑](#4.2 原理拆解：Adam的核心逻辑)
    • [4.3 公式推导（严谨版）](#4.3 公式推导（严谨版）)
    • [4.4 实操细节（避坑重点，工业界落地必备）](#4.4 实操细节（避坑重点，工业界落地必备）)
    • [4.6 小结](#4.6 小结)
  • 五、四大算法总结与关联对比（重中之重，帮你串联知识）
  • • [5.1 核心关联总结](#5.1 核心关联总结)
    • [5.2 四大算法核心差异对比表（直接收藏，快速查阅）](#5.2 四大算法核心差异对比表（直接收藏，快速查阅）)
    • [5.3 新手实操建议（避坑指南）](#5.3 新手实操建议（避坑指南）)
  • 结尾

深度学习优化器详解：EWA、Momentum、RMSprop、Adam 从原理到实操

在深度学习模型训练中，"优化器"是决定模型能否快速收敛、避免过拟合、达到最优性能的核心组件。而指数加权平均（EWA）、动量梯度下降（Momentum）、RMSprop、Adam 这四个算法，更是贯穿了优化器的发展历程------EWA是基础工具，Momentum解决梯度震荡，RMSprop解决学习率适配，Adam则融合三者优势成为工业界标配。

本文将从「新手能懂的通俗逻辑」出发，结合公式推导、实操细节和配图建议，逐一拆解这四个算法，帮你彻底搞懂它们的核心原理、适用场景和内在关联，再也不用死记硬背公式，也能轻松区分不同优化器的差异。

开篇铺垫：为什么需要这些优化算法？

在学习具体算法前，我们先搞懂一个核心问题：传统的小批量梯度下降（SGD）有什么痛点，为什么需要这些优化算法来"升级"？

传统SGD的核心逻辑是：每次用一个批次的样本计算梯度，然后沿梯度反方向更新参数，公式为： W t = W t − 1 − η ⋅ g t W_{t} = W_{t-1} - \eta \cdot g_t Wt=Wt−1−η⋅gt（ W W W为权重， η \eta η为学习率， g t g_t gt为当前梯度）。

但它有两个致命痛点，也是后续所有优化算法要解决的问题：

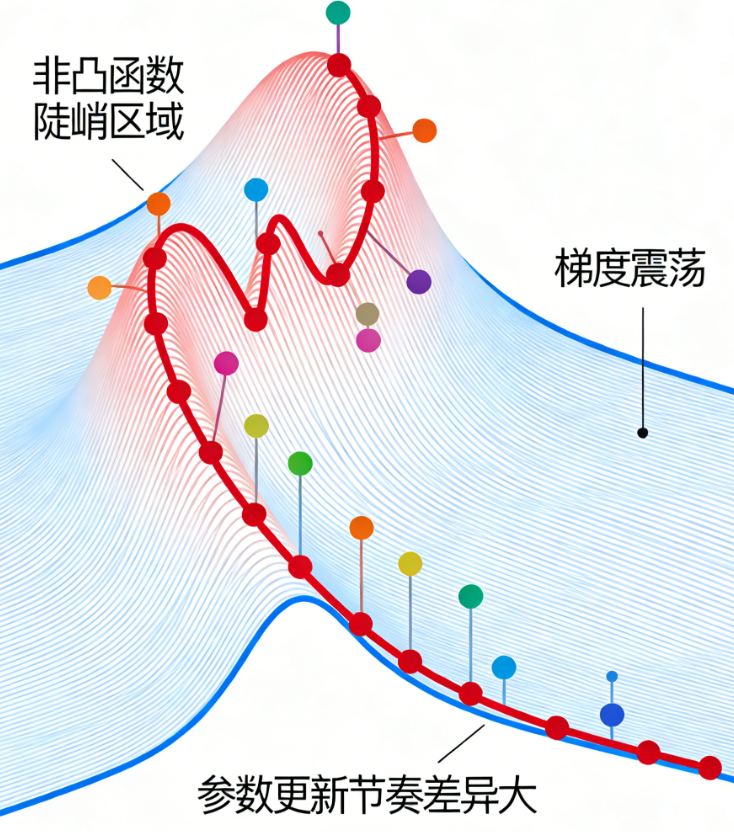
• 梯度震荡严重：当梯度波动大（如非凸函数的陡峭区域），SGD会在最优解附近来回震荡，收敛速度极慢；

• 学习率固定不变：所有参数用同一个学习率更新，而不同参数的梯度大小、波动程度差异极大（如有的参数梯度一直很小，有的忽大忽小），导致"有的参数更新太慢，有的参数更新太猛"。

而我们接下来要讲的四个算法，正是围绕这两个痛点展开：EWA提供"平滑工具"，Momentum用平滑解决震荡，RMSprop用平滑适配学习率，Adam融合二者实现"又快又稳"。

一、基础工具：指数加权平均（EWA）------ 所有优化器的"平滑基石"

指数加权平均（Exponential Weighted Average，简称EWA），并不是一个"优化器"，而是一个「通用的序列数据平滑工具」------它的核心作用是"过滤序列中的随机噪声，保留真实趋势"，后续的Momentum、RMSprop、Adam，都用到了EWA的核心逻辑。

1.1 核心背景：为什么需要"平滑"？

深度学习训练中，我们会得到很多"序列数据"：比如每一轮batch的loss值、每一轮的梯度值。这些数据往往存在大量随机噪声（如某一轮batch的loss突然飙升/骤降），直接使用这些原始数据会导致模型训练不稳定（如参数更新震荡）。

EWA的出现，就是为了"平滑这些噪声"------它通过对历史数据按「指数级衰减的权重」做加权平均，让越新的数据权重越高、越旧的数据权重越低，既保留了新数据的响应速度，又过滤了旧数据的噪声。

1.2 原理拆解：EWA的核心逻辑（通俗版）

举个生活中的例子：我们想计算"最近10天的平均气温"，有两种方法：

• 简单移动平均：保存最近10天的气温，每天取这10天的平均值------缺点是需要保存10天的数据，且第10天和第1天的权重相同，无法体现"近期气温更重要"；

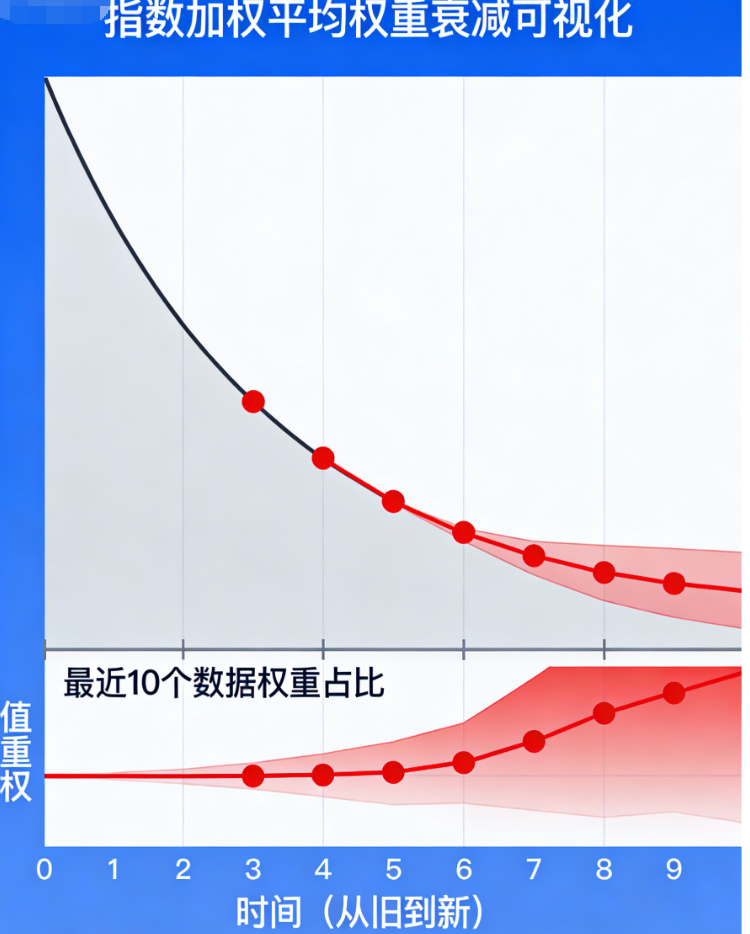
• 指数加权平均：不用保存所有历史气温，只需要保存上一次的平滑气温，每天用"上一次平滑值×0.9 + 当天气温×0.1"计算当天的平滑气温------越新的气温权重越高，越旧的气温权重按0.9的指数衰减，既高效又贴合实际。

这就是EWA的核心：用「迭代计算」替代「保存历史数据」，用「指数衰减权重」替代「等权平均」，实现高效平滑。

1.3 公式推导（严谨版，新手可跳过推导看结论）

EWA的迭代公式如下（ t t t为当前迭代轮次）：

v t = β ⋅ v t − 1 + ( 1 − β ) ⋅ θ t v_t = \beta \cdot v_{t-1} + (1 - \beta) \cdot \theta_t vt=β⋅vt−1+(1−β)⋅θt

各参数含义：

• v t v_t vt：当前轮次的平滑值（最终输出）；

• v t − 1 v_{t-1} vt−1：上一轮次的平滑值（初始值 v 0 = 0 v_0=0 v0=0）；

• β \beta β：衰减系数（取值范围[0,1)），控制历史数据的权重；

• θ t \theta_t θt：当前轮次的原始数据（如当前batch的loss、当前的梯度）；

• ( 1 − β ) (1 - \beta) (1−β)：当前数据的权重。

我们将公式展开，可以更清晰地看到权重分布：

v t = ( 1 − β ) θ t + β ( 1 − β ) θ t − 1 + β 2 ( 1 − β ) θ t − 2 + ⋯ + β k ( 1 − β ) θ t − k + ... v_t = (1-\beta)\theta_t + \beta(1-\beta)\theta_{t-1} + \beta^2(1-\beta)\theta_{t-2} + \dots + \beta^k(1-\beta)\theta_{t-k} + \dots vt=(1−β)θt+β(1−β)θt−1+β2(1−β)θt−2+⋯+βk(1−β)θt−k+...

可见：每一个历史数据 θ t − k \theta_{t-k} θt−k的权重的是 β k ( 1 − β ) \beta^k(1-\beta) βk(1−β)，随 k k k（历史步数）增大呈指数级衰减------越旧的数据，权重越小，最终趋近于0。

1.4 关键细节： β \beta β的选择与有效窗口（实操重点）

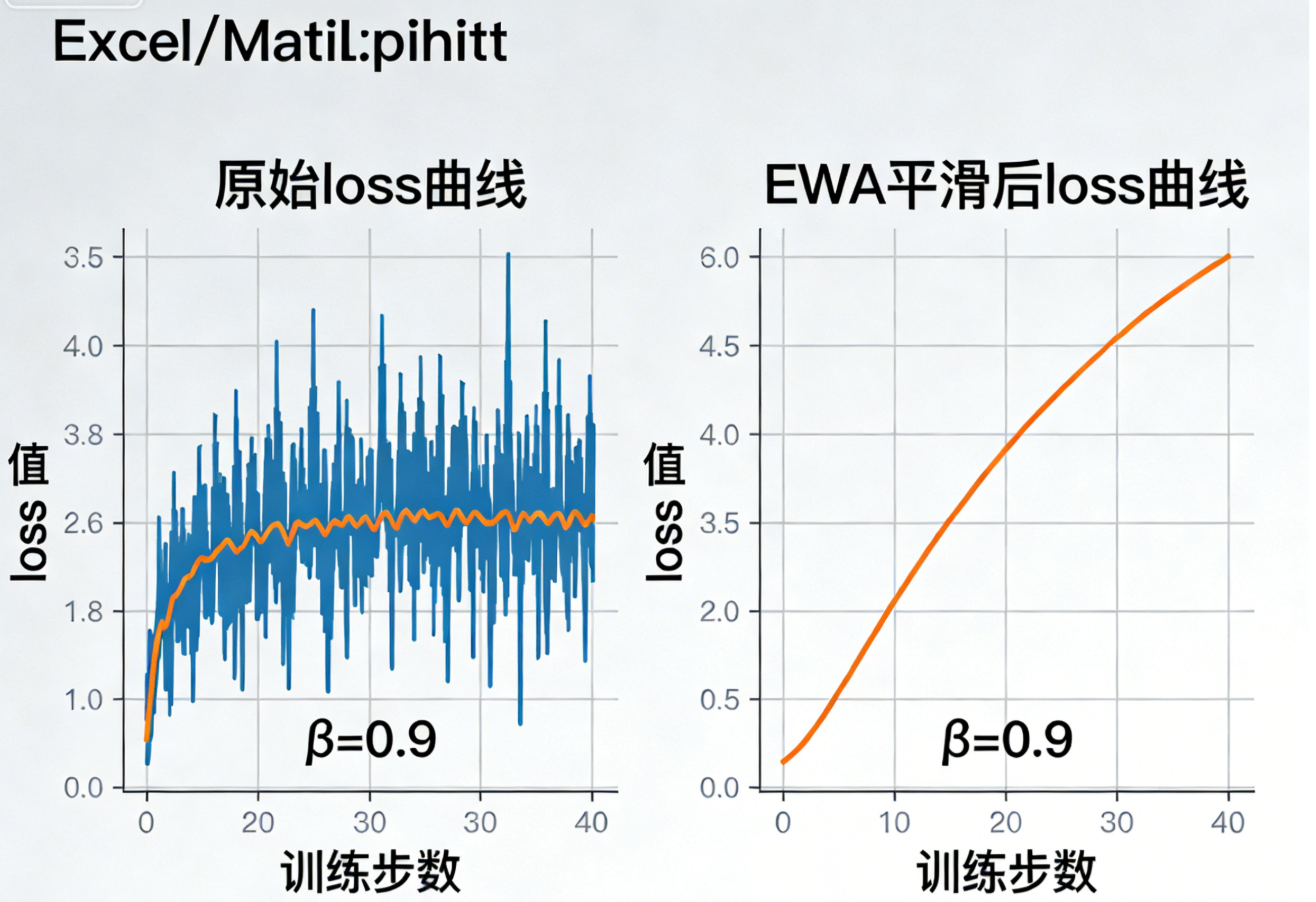
β \beta β是EWA唯一的超参，它的取值直接决定平滑效果和响应速度，核心规律的是： β \beta β越大，平滑效果越强，响应速度越慢； β \beta β越小，响应速度越快，平滑效果越弱。

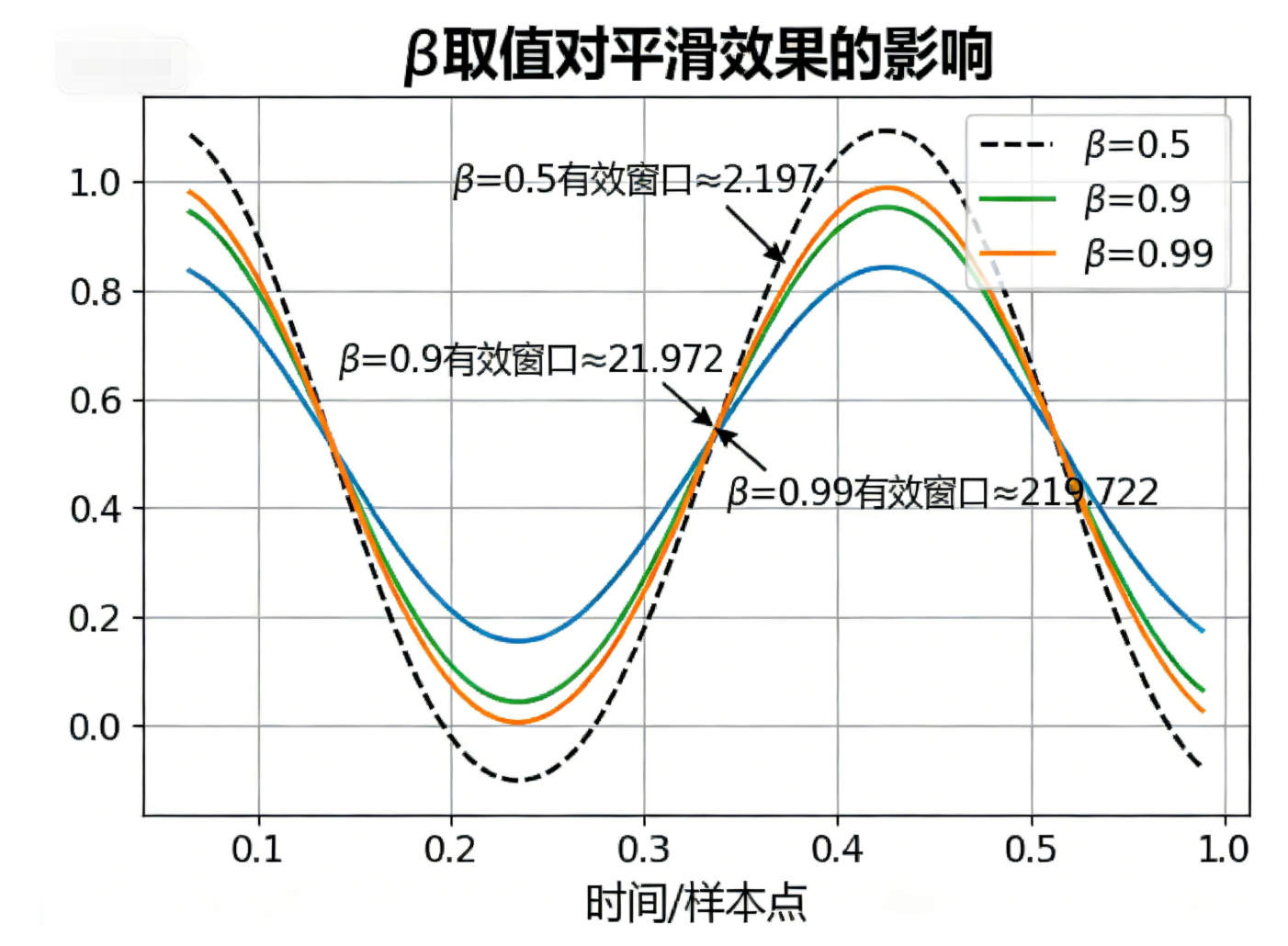
工业界有一个「有效窗口近似公式」，可以快速判断 β \beta β对应的"等效平均数据量"：

有效窗口大小 ≈ 1 1 − β 有效窗口大小 \approx \frac{1}{1 - \beta} 有效窗口大小≈1−β1

常见 β \beta β取值及对应场景（直接套用）：

β \beta β取值	有效窗口大小	平滑效果	适用场景
0.5	≈2	弱平滑，响应极快	对新数据敏感的场景（如实时监控）
0.9	≈10	常规平滑，兼顾速度与效果	深度学习loss/梯度平滑（最常用）
0.95	≈20	中等强平滑	梯度波动较大的场景
0.99	≈100	强平滑，响应较慢	慢变化的时间序列（如模型精度监控）

1.6 小结

EWA的核心价值是「高效平滑」：用O(1)的计算/内存成本，实现对序列数据的噪声过滤，且能灵活调整响应速度。它不是优化器，但却是后续所有高级优化器的"基础工具"------Momentum用它平滑梯度，RMSprop用它平滑梯度平方，Adam则两者都用。

二、第一代优化器：动量梯度下降（Momentum）------ 解决梯度震荡，加速收敛

Momentum（动量）是在传统SGD基础上的第一次"升级"，核心目标是「解决梯度震荡问题，加速模型收敛」------它的核心思路的是：用EWA平滑梯度序列，让梯度更新"带有惯性"，避免在陡峭区域来回震荡。

2.1 核心背景：Momentum要解决的痛点

传统SGD的最大痛点之一是「梯度震荡」：当训练数据存在噪声，或者模型损失函数是非凸函数（大多数深度学习模型都是非凸）时，梯度会出现剧烈波动，导致参数更新在最优解附近来回"摇摆"，收敛速度极慢。

举个例子：就像一个小球从山坡上滚下来（目标是滚到山底，即最优解），传统SGD的小球会在山坡的沟壑中来回碰撞、震荡，很难快速滚到山底；而Momentum给小球加上"惯性"，让它忽略小的沟壑（噪声），沿着山坡的整体趋势快速下滑。

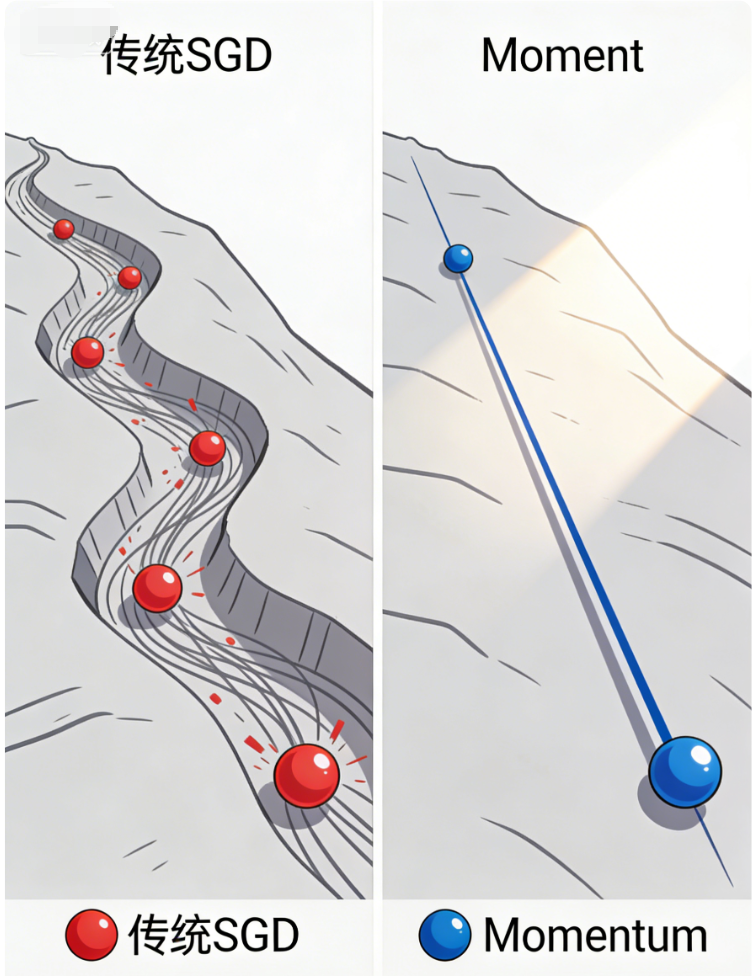
2.2 原理拆解：Momentum的核心逻辑

Momentum的本质是「用EWA平滑梯度，再用平滑后的梯度更新参数」------它没有改变SGD的参数更新方向，只是通过平滑梯度 ，减少了更新过程中的震荡，让更新方向更"稳定"。

通俗来说：Momentum会"记住"上一轮的梯度方向和大小，将其与当前梯度融合（平滑），然后沿着融合后的方向更新参数------如果连续多轮的梯度方向一致（如都是向下的梯度），则参数更新步长会越来越大（加速收敛）；如果梯度方向突变（如噪声导致），则会被平滑掉（减少震荡）。

2.3 公式推导

Momentum的参数更新分为两步：第一步用EWA平滑梯度，第二步用平滑后的梯度更新权重。

步骤1：用EWA平滑梯度（核心，复用EWA公式）

v t = β ⋅ v t − 1 + ( 1 − β ) ⋅ g t v_t = \beta \cdot v_{t-1} + (1 - \beta) \cdot g_t vt=β⋅vt−1+(1−β)⋅gt

步骤2：用平滑后的梯度 v t v_t vt更新参数

W t = W t − 1 − η ⋅ v t W_t = W_{t-1} - \eta \cdot v_t Wt=Wt−1−η⋅vt

各参数含义（补充说明）：

• v t v_t vt：当前轮次平滑后的梯度（也叫"动量项"）；

• g t g_t gt：当前轮次的原始梯度（和传统SGD的梯度计算一致）；

• β \beta β：动量系数（衰减系数），常用取值0.9（对应有效窗口≈10，平滑最近10轮的梯度）；

• η \eta η：学习率（和传统SGD一致，无需额外调参）；

• W t W_t Wt：当前轮次更新后的权重。

关键注意：Momentum的 β \beta β和EWA的 β \beta β含义一致，都是控制历史数据的权重------ β = 0.9 \beta=0.9 β=0.9时，平滑最近10轮的梯度，既能过滤噪声，又能保留梯度的整体趋势。

2.4 实操细节（避坑重点）

1. β \beta β的取值：默认0.9（工业界通用），无需频繁调参；若梯度震荡特别严重，可调整为0.95；若想加快响应速度，可调整为0.8；

2. 学习率 η \eta η：和传统SGD的学习率设置一致（如0.01、0.001），Momentum不改变学习率的大小，只改变梯度的方向和稳定性；

3. 偏差修正：初始阶段（前几轮）， v 0 = 0 v_0=0 v0=0，平滑后的梯度 v t v_t vt会偏低，可做偏差修正（ v t / ( 1 − β t ) v_t / (1 - \beta^t) vt/(1−βt)），后续 β t \beta^t βt趋近于0，修正项可忽略；

4. 适用场景：梯度波动大、非凸损失函数的场景（如CNN、RNN训练），比传统SGD收敛快2~3倍。

2.6 小结

Momentum的核心是「用EWA平滑梯度，给参数更新加上惯性」------它解决了传统SGD梯度震荡的痛点，加速了模型收敛，但没有解决"学习率固定"的问题：所有参数依然用同一个学习率更新，不同参数的更新步调依然不一致。

三、第二代优化器：RMSprop ------ 自适应学习率，解决更新步调不一致

RMSprop（Root Mean Square Propagation，均方根传播）是在Momentum基础上的第二次"升级"，核心目标是「解决"学习率固定"的痛点，为每个参数自适应调整学习率」------它的核心思路是：用EWA平滑梯度的平方，再用其平方根缩放学习率，让梯度波动大的参数学习率变小，梯度波动小的参数学习率变大。

3.1 核心背景：RMSprop要解决的痛点

Momentum解决了梯度震荡，但依然存在一个致命问题：「全局学习率固定」。

在深度学习模型中，不同参数的梯度特性差异极大：比如模型的词嵌入层参数，梯度可能一直很小（更新太慢）；而模型的全连接层参数，梯度可能忽大忽小（更新太震荡）。如果所有参数用同一个学习率，会导致：

• 梯度波动大的参数：学习率太大 → 更新过度、震荡；

• 梯度波动小的参数：学习率太小 → 收敛太慢。

RMSprop的出现，就是为了"给每个参数定制学习率"------它通过平滑梯度的平方，衡量每个参数的梯度波动程度，然后根据波动程度自适应调整学习率，实现"因材施教"。

3.2 原理拆解：RMSprop的核心逻辑

RMSprop的本质是「用EWA平滑梯度的平方，再用其平方根缩放学习率」------它的核心创新点是：不直接平滑梯度，而是平滑"梯度的平方"，以此衡量梯度的波动程度。

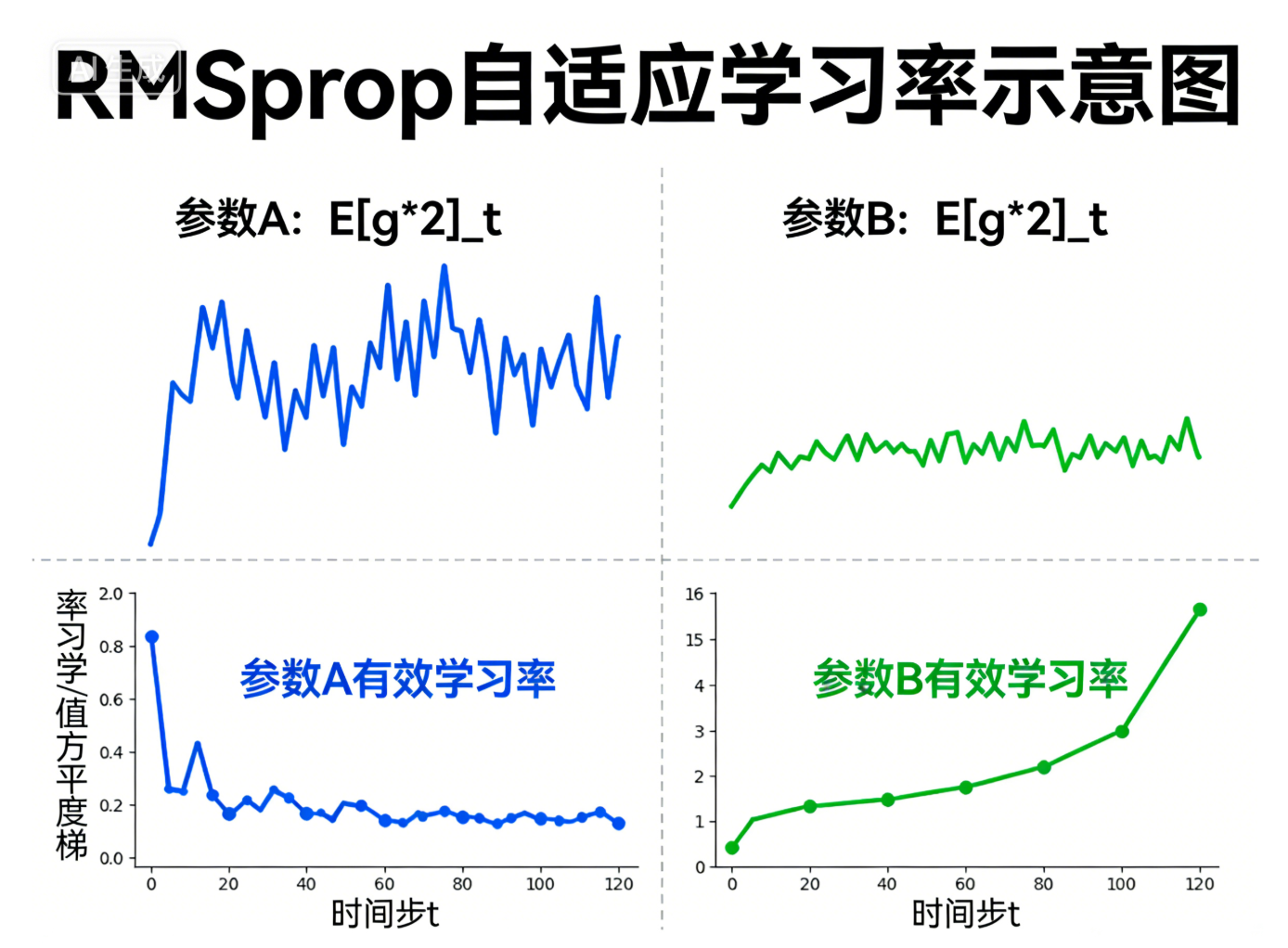
通俗来说：

• 对于某一个参数，如果它的梯度波动很大（梯度平方的平滑值大），说明这个参数的更新需要"谨慎"，RMSprop会自动减小它的有效学习率，避免更新过度；

• 对于某一个参数，如果它的梯度波动很小（梯度平方的平滑值小），说明这个参数的更新需要"加快"，RMSprop会自动增大它的有效学习率，加速收敛。

这里有一个关键细节：梯度的正负仅表示更新方向，波动大小由绝对值决定，因此我们用"梯度的平方"来衡量波动程度------既可以统一衡量波动，又能避免正负梯度抵消。

3.3 公式推导（严谨版）

RMSprop的参数更新分为三步，依然复用EWA的核心逻辑，重点是"平滑梯度平方"：

步骤1：计算当前梯度的平方（消除正负影响，衡量波动）

g t 2 = ( g t ) ⋅ ( g t ) g_t^2 = (g_t) \cdot (g_t) gt2=(gt)⋅(gt)

步骤2：用EWA平滑梯度的平方（核心，复用EWA公式）

E [ g 2 ] t = β ⋅ E [ g 2 ] t − 1 + ( 1 − β ) ⋅ g t 2 E[g^2]t = \beta \cdot E[g^2]{t-1} + (1 - \beta) \cdot g_t^2 E[g2]t=β⋅E[g2]t−1+(1−β)⋅gt2

步骤3：用平滑后的梯度平方的平方根，缩放学习率，更新参数

W t = W t − 1 − η E [ g 2 ] t + ϵ ⋅ g t W_t = W_{t-1} - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} \cdot g_t Wt=Wt−1−E[g2]t+ϵ η⋅gt

各参数含义（补充说明）：

• E [ g 2 ] t E[g^2]_t E[g2]t：当前轮次平滑后的梯度平方（衡量梯度波动程度）；

• β \beta β：衰减系数，常用取值0.9（平滑最近10轮的梯度平方）；

• ϵ \epsilon ϵ：极小值（如 1 e − 8 1e-8 1e−8），避免分母为0（防止梯度平方为0时，除法报错）；

• η E [ g 2 ] t + ϵ \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} E[g2]t+ϵ η：每个参数的「自适应有效学习率」------梯度波动越大，有效学习率越小。

3.4 实操细节（避坑重点）

1. 超参选择： β \beta β默认0.9， ϵ \epsilon ϵ默认1e-$，无需调整；学习率 η \eta η默认0.001（比传统SGD小1~2个数量级），可根据任务微调；

2. 核心优势：无需手动调整学习率，每个参数自适应调整，解决了不同参数更新步调不一致的问题；

3. 与Momentum的区别：Momentum平滑梯度（解决震荡），RMSprop平滑梯度平方（适配学习率），二者解决的是不同痛点；

4. 适用场景：梯度稀疏、波动大的场景（如自然语言处理的词嵌入训练、图像分割的边缘参数训练），比Momentum收敛更稳定。

3.6 小结

RMSprop的核心是「用EWA平滑梯度平方，实现自适应学习率」------它解决了传统SGD和Momentum"学习率固定"的痛点，让每个参数都能获得合适的学习率，收敛更稳定。但它没有解决"梯度方向的惯性"问题，而Adam算法则融合了Momentum和RMSprop的优势，成为了工业界的"终极选择"。

四、终极优化器：Adam ------ 融合Momentum与RMSprop，工业界标配

Adam（Adaptive Moment Estimation，自适应动量估计）是目前深度学习中最常用、最通用的优化器------它的核心逻辑非常简单：「融合Momentum的梯度平滑（惯性）和RMSprop的自适应学习率（缩放）」，同时解决了梯度震荡和学习率固定两个痛点，实现了"又快又稳"的收敛。

通俗来说：Adam = Momentum（平滑梯度，加惯性） + RMSprop（平滑梯度平方，自适应学习率），相当于给"小球"既加上了惯性（减少震荡），又加上了"自适应调速器"（根据路况调整速度），能最快、最稳地滚到山底（最优解）。

4.1 核心背景：Adam要解决的痛点

Momentum解决了梯度震荡，但学习率固定；RMSprop解决了学习率固定，但没有梯度惯性------Adam的出现，就是为了"融合二者的优势"，同时解决这两个痛点：

• 保留Momentum的梯度平滑（惯性）：减少梯度震荡，加速收敛；

• 保留RMSprop的自适应学习率：为每个参数定制学习率，解决更新步调不一致；

• 额外优化：加入偏差修正，解决初始阶段平滑值偏低的问题，让收敛更稳定。

正是因为这种"全能性"，Adam成为了工业界的标配优化器------无论是CNN、RNN、Transformer，还是大模型训练，Adam几乎都是首选。

4.2 原理拆解：Adam的核心逻辑

Adam的核心逻辑分为三步，本质是"同时平滑梯度和梯度平方，再结合二者更新参数"：

1. 用EWA平滑梯度（复用Momentum的逻辑）：得到带有惯性的平滑梯度，减少震荡；

2. 用EWA平滑梯度的平方（复用RMSprop的逻辑）：得到梯度波动程度，用于自适应调整学习率；

3. 对两个平滑值做偏差修正（Adam的创新点）：解决初始阶段平滑值偏低的问题，然后用平滑后的梯度和梯度平方，更新参数。

4.3 公式推导（严谨版）

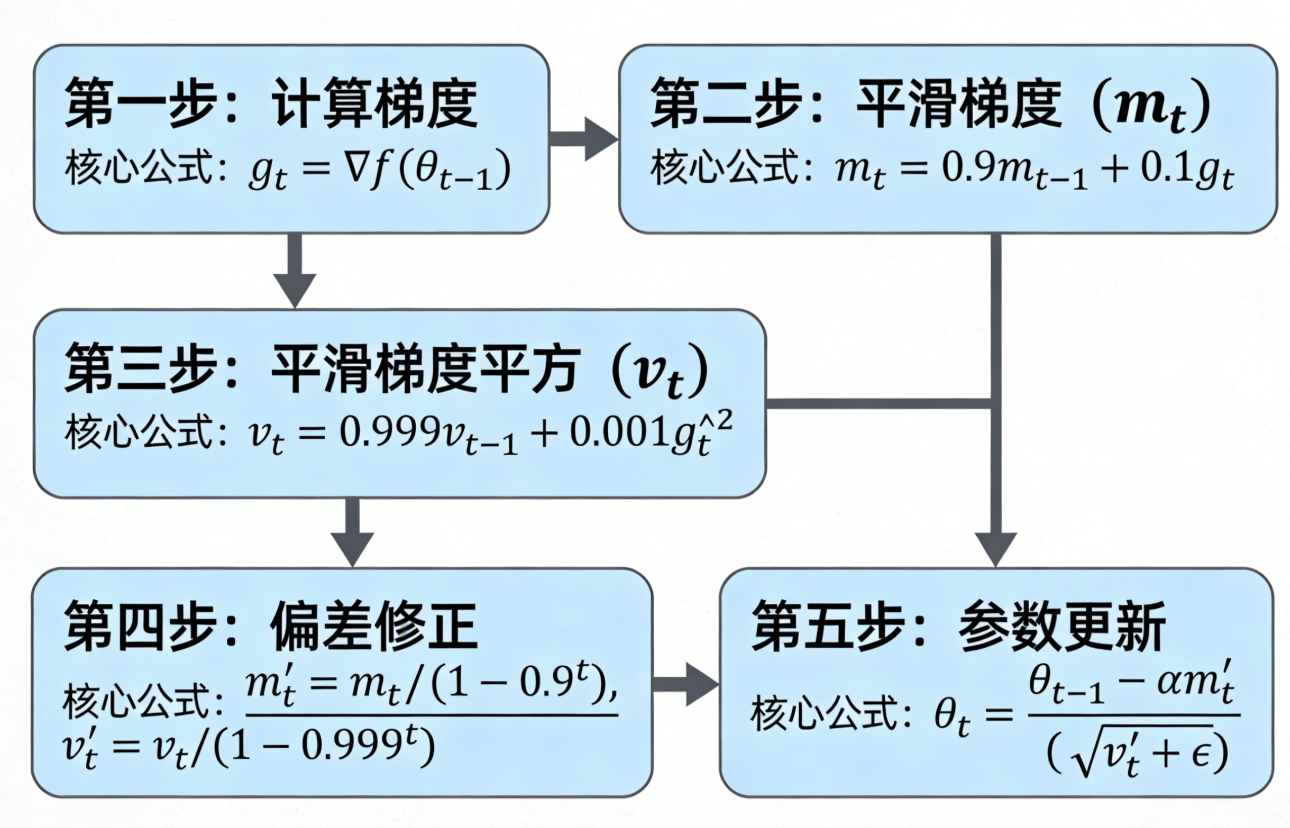
Adam的参数更新分为四步，步骤清晰，复用了前面两个算法的核心公式，重点是"双平滑+偏差修正"：

步骤1：用EWA平滑梯度（Momentum逻辑）

m t = β 1 ⋅ m t − 1 + ( 1 − β 1 ) ⋅ g t m_t = \beta_1 \cdot m_{t-1} + (1 - \beta_1) \cdot g_t mt=β1⋅mt−1+(1−β1)⋅gt

步骤2：用EWA平滑梯度的平方（RMSprop逻辑）

v t = β 2 ⋅ v t − 1 + ( 1 − β 2 ) ⋅ g t 2 v_t = \beta_2 \cdot v_{t-1} + (1 - \beta_2) \cdot g_t^2 vt=β2⋅vt−1+(1−β2)⋅gt2

步骤3：对两个平滑值做偏差修正（Adam创新点）

m ^ t = m t 1 − β 1 t \hat{m}_t = \frac{m_t}{1 - \beta_1^t} m^t=1−β1tmt

v ^ t = v t 1 − β 2 t \hat{v}_t = \frac{v_t}{1 - \beta_2^t} v^t=1−β2tvt

步骤4：用修正后的平滑值，更新参数（自适应学习率+惯性）

W t = W t − 1 − η ⋅ m ^ t v ^ t + ϵ W_t = W_{t-1} - \eta \cdot \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} Wt=Wt−1−η⋅v^t +ϵm^t

各参数含义（重点说明）：

• m t m_t mt：平滑后的梯度（类似Momentum的动量项，带惯性）；

• v t v_t vt：平滑后的梯度平方（类似RMSprop的波动项，用于自适应学习率）；

• β 1 \beta_1 β1：梯度平滑的衰减系数（对应Momentum的 β \beta β），默认0.9；

• β 2 \beta_2 β2：梯度平方平滑的衰减系数（对应RMSprop的 β \beta β），默认0.999；

• m ^ t \hat{m}_t m^t、 v ^ t \hat{v}_t v^t：修正后的平滑值，解决初始阶段 m 0 = 0 m_0=0 m0=0、 v 0 = 0 v_0=0 v0=0导致的平滑值偏低问题；

• η \eta η：基础学习率，默认0.001； ϵ \epsilon ϵ：默认 1 e − 8 1e-8 1e−8，避免分母为0。
  

4.4 实操细节（避坑重点，工业界落地必备）

1. 超参选择（几乎无需调整，直接套用）：

   • β 1 = 0.9 \beta_1=0.9 β1=0.9， β 2 = 0.999 \beta_2=0.999 β2=0.999， ϵ = 1 e − 8 \epsilon=1e-8 ϵ=1e−8；

   • 学习率 η \eta η默认0.001，若模型收敛太慢，可调整为0.01；若震荡严重，可调整为0.0001。

2. 偏差修正的作用：初始阶段（前10轮左右），修正项的作用明显，能让平滑值更准确；训练后期， β 1 t \beta_1^t β1t、 β 2 t \beta_2^t β2t趋近于0，修正项可忽略，不影响收敛；

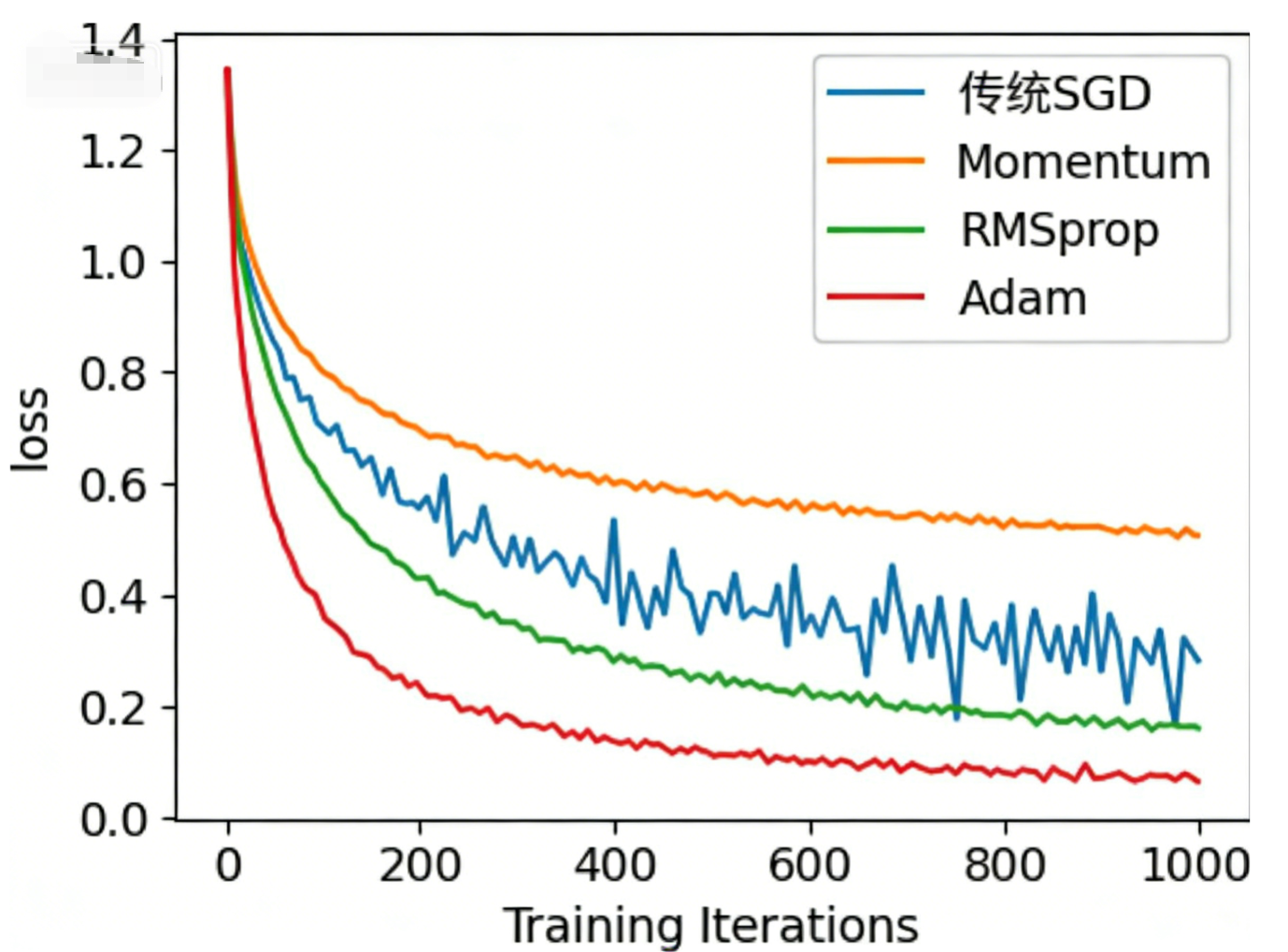
3. 与其他优化器的对比：

   • 比传统SGD：收敛快、震荡小；

   • 比Momentum：自适应学习率，无需手动调参；

   • 比RMSprop：带梯度惯性，收敛更快。

4. 适用场景：所有深度学习场景（CNN、RNN、Transformer、大模型训练），是工业界的"首选优化器"；

5. 常见变体：AdamW（Adam+L2正则化），解决Adam中L2正则化效果不佳的问题，目前大模型训练中更常用AdamW。

4.6 小结

Adam的核心是「融合Momentum和RMSprop的优势，加上偏差修正」------它既解决了梯度震荡问题（用EWA平滑梯度），又解决了学习率固定问题（用EWA平滑梯度平方，自适应学习率），同时通过偏差修正让收敛更稳定。正是这种"全能性"，让Adam成为了深度学习中最常用的优化器，也是新手入门、工业界落地的首选。

五、四大算法总结与关联对比（重中之重，帮你串联知识）

到这里，我们已经逐一拆解了EWA、Momentum、RMSprop、Adam四个算法，它们之间不是孤立的，而是「层层递进、相互融合」的关系------EWA是基础，Momentum和RMSprop是在EWA基础上的单维度优化，Adam是融合二者的终极优化。

5.1 核心关联总结

• EWA：所有算法的"平滑基石"，Momentum用它平滑梯度，RMSprop用它平滑梯度平方，Adam两者都用；

• Momentum = SGD + EWA（平滑梯度）：解决梯度震荡，加速收敛；

• RMSprop = SGD + EWA（平滑梯度平方）：解决学习率固定，自适应调整步调；

• Adam = Momentum + RMSprop + 偏差修正：融合二者优势，又快又稳，工业界标配。

5.2 四大算法核心差异对比表（直接收藏，快速查阅）

算法	核心作用	核心逻辑	关键超参	适用场景
EWA	序列数据平滑（工具）	指数衰减权重，迭代平滑序列	β \beta β（0.9最常用）	loss/梯度平滑，所有优化器的基础
Momentum	减少梯度震荡，加速收敛	EWA平滑梯度，加惯性	β \beta β（0.9）、 η \eta η	梯度波动大、非凸函数场景
RMSprop	自适应学习率，解决步调不一致	EWA平滑梯度平方，缩放学习率	β \beta β（0.9）、 η \eta η、 ϵ \epsilon ϵ	梯度稀疏、波动大的场景（NLP/CV）
Adam	又快又稳，自适应收敛	融合Momentum+RMSprop+偏差修正	β 1 \beta_1 β1（0.9）、 β 2 \beta_2 β2（0.999）、 η \eta η	所有深度学习场景（工业界首选）

5.3 新手实操建议（避坑指南）

1. 入门阶段：直接使用Adam优化器，默认超参（ β 1 = 0.9 \beta_1=0.9 β1=0.9， β 2 = 0.999 \beta_2=0.999 β2=0.999， η = 0.001 \eta=0.001 η=0.001），无需手动调参，能解决90%的场景；

2. 若模型震荡严重：可适当减小学习率 η \eta η，或改用AdamW（加入L2正则化）；

3. 若模型收敛太慢：可适当增大学习率 η \eta η，或检查数据预处理、模型结构，而非盲目更换优化器；

4. 理解优先级：先懂EWA的平滑逻辑，再懂Momentum和RMSprop的优化方向，最后理解Adam的融合逻辑------不用死记公式，重点理解"每个算法解决了什么痛点"。

结尾

深度学习优化器的发展，本质是"不断解决传统SGD的痛点"------从EWA提供平滑工具，到Momentum解决震荡，再到RMSprop适配学习率，最后到Adam融合所有优势，每一步都在朝着"更高效、更稳定、更易用"的方向前进。