🏗️ 本博客是阅读完两篇文献：《Robust Face Recognition via Sparse Representation》和《Robust Face Recognition via Adaptive Sparse Representation》的整理。个人理解！
在图像识别的浩瀚星图中，如何"表示"一张图像是贯穿始终的核心问题。长久以来，我们习惯于先"提取特征"，再"训练分类器"（如SVM、神经网络）。然而，一种名为稀疏表示 的范式带来了根本性的转变：它不急于将图像压缩为特征，而是追问------我们能否直接用整个训练集来"线性表达"一张未知图像，并让这种表达方式本身揭示其身份？
📝本文将深入剖析这一革命性范式的奠基之作------稀疏表示分类 ，并解读其关键演进------自适应稀疏表示。我们将看到，从追求极致稀疏到智能平衡相关性，其背后是一脉相承的数学优雅与统一思想。
🎯第一部分：基石------SRC，稀疏线性表示的优雅
1.1 核心洞见：从子空间假设出发
SRC建立在人脸图像的一个优雅假设上：同一人脸在不同光照、表情下的所有图像，张成了一个低维线性子空间 （即"人脸子空间"）。这意味着，给定足够多的训练样本，一张新的、同一人的测试图像 y∈Rm，几乎肯定能由该人对应的训练图像线性组合而成：
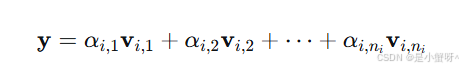
其中，是第 i 个人的第 j 张训练图像
既然我们事先不知道测试图像属于谁，SRC采取了一个大胆的策略：将所有人的训练样本拼接成一个巨型字典矩阵 A：
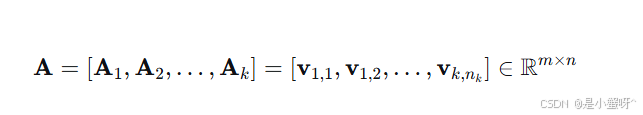
于是，线性表示问题可以重写为：
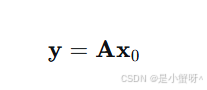
这里，系数向量 的形态至关重要 。如果 y 来自第 i 个人，理想的
应该仅在对应第 i 类样本的位置上有非零值，在其他类对应的位置上全为零。在一个包含众多类别的人脸库中，这样的
是高度稀疏的------它的绝大多数元素都是零。
至此，人脸识别问题被巧妙地转化为一个线性方程组的求解问题 ，而解向量 **
**的稀疏模式直接编码了身份信息。
1.2 优化求解：ℓ¹最小化的魔法
然而，直接求解 并寻找最稀疏的解（即非零元素最少的解，称为 ℓ0 数最小化）是一个众所周知的NP难问题，无法高效求解。
SRC的关键贡献：在于引入了来自压缩感知（Compressed Sensing） 的理论工具：在字典矩阵 A 满足一定条件时，ℓ⁰这个组合优化难题，可以等价地转化为一个凸优化问题------ℓ¹范数最小化。
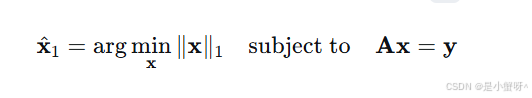
这里，ℓ¹-范数 ∥x∥1=∑i∣xi∣。这个转变是革命性的，因为凸优化问题存在高效、可靠的求解算法（如线性规划）。当存在噪声或遮挡时，约束可以放宽：
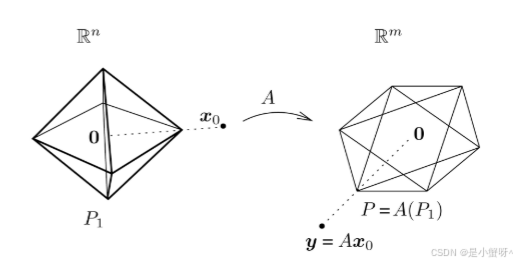
1.3 几何解释：为什么ℓ¹能带来稀疏解？
++ℓ¹最小化为何偏爱稀疏解？一个极其直观的解释来自几何。++
考虑所有满足 ℓ¹-范数小于等于1的向量集合 P1={x:∥x∥1≤1}，它在二维下是一个菱形（高维下是"交叉多面体"）。字典矩阵 A 将这个ℓ¹球线性映射到特征空间，形成一个多面体
求解 ℓ¹ 最小化，等价于从原点出发，按比例放大这个ℓ¹球（即考虑 λP1），直到其映像 A(λP1) 刚好"碰到"测试点 y。此时的放大系数 λ 就是解向量的ℓ¹范数。
关键在于 ：多面体 A(P1) 的"尖端"或"棱角"是其低维面，这些点对应着原空间 P1 中非常稀疏的向量（即顶点或面上的点）。由于 ℓ¹ 球本身的形状是"有尖角的"，其映像的尖端也最容易"刺中"数据点 y，这就使得求得的解向量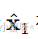 
有很大概率是稀疏的。
1.4 分类决策：最小重建残差
++得到稀疏系数 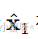后，如何分类？SRC再次采用了一种简洁而有力的方式。++
定义选择函数 δi: Rn→Rn，它只保留系数向量中对应第 i 类的分量，其余全部置零。然后，用这些被筛选出的系数，配合字典 A，对测试图像进行部分重建：
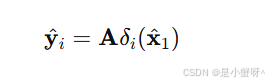
如果 y 真的属于第 i 类，那么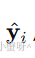
应该非常接近 y。因此，我们只需计算每个类别下的重建残差，并将测试样本判给残差最小的那一类：
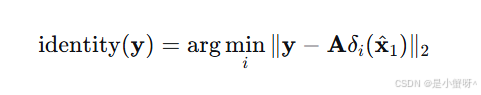
💡第二部分：演进------ASRC，自适应平衡的艺术
2.1 SRC的局限：当"稀疏性"遭遇"相关性"
SRC取得了巨大成功，但其对"稀疏性"的极致追求也隐含了一个弱点。ℓ¹ 范数倾向于在高度相关的候选特征（字典原子）中随机挑选一个，而不是将它们作为一个群体来选择。
在人脸识别中，如果同一个人的多张训练照片（例如不同光照）彼此非常相似（高度相关），SRC可能只会从中不稳定地选出一张作为代表，而忽略其他同样有价值的、信息互补的相关样本。这导致了表示的不稳定性和信息损失。
2.2 核心创新：引入迹范数（Trace Norm）作为相关性适配器
自适应稀疏表示（ASRC）的核心思想是：正则化项应该既能促进稀疏性，又能感知并适应数据内部的相关性结构 。为此，它引入了迹范数（Trace Norm 或 Nuclear Norm） 作为正则化器。
ASRC定义了一个新颖的相关性正则化项：
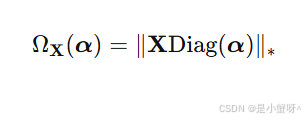
其中：
-
X∈Rm×n是训练字典矩阵。
-
α∈Rn 是我们要求解的表示系数向量。
-
Diag(α) 是将向量 α 转换为对角矩阵的操作。
-
∥⋅∥∗ 表示矩阵的迹范数，即矩阵所有奇异值之和。
这个构造 XDiag(α) 非常精妙：它产生了一个新矩阵，其第 j 列是原始字典的第 j 个原子 xj，但按系数 αj 进行了缩放。对这个矩阵求迹范数，能够同时捕捉到字典原子 X 的列间相关性和系数 α 的幅值信息。
2.3 自适应性的数学证明：连接ℓ¹与ℓ²的桥梁
ASRC最精彩的部分在于，它证明了其正则化项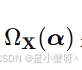 
，是ℓ¹和ℓ²范数在几何上的自适应内插。
考虑两个极端情况：
- 当字典 X 的列向量两两正交时（样本完全不相关）：
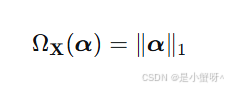
此时ASRC完全退化为SRC，强调极致的稀疏性。
2.当字典 X 的所有列向量完全共线时（样本完全相关）：
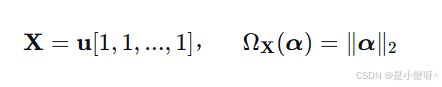
此时ASRC退化为类似CRC（协同表示）的方法，强调群体的协同作用。
对于一般的、介于正交和共线之间的字典 X，有如下不等式恒成立：
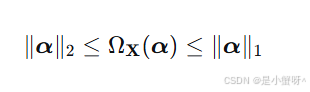
这意味着，迹范数正则化项的值，由数据 X 本身的相关性结构决定，自动落在
ℓ¹和ℓ²范数之间 。ASRC不需要人工设定选择ℓ¹还是ℓ²，而是让数据自己说话，实现从"稀疏选择"到"协同表示"的连续、平滑的自适应过渡。
2.4 统一的优化框架
综合以上，ASRC提出的完整优化模型（考虑鲁棒性）为：
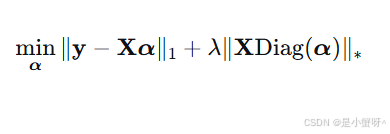
其中：
-
第一项
是使用ℓ¹损失度量的重建误差，使其对遮挡和异常值更鲁棒。 -
第二项
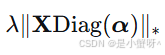就是我们介绍的自适应相关性正则项，λ 是平衡参数。 -
这个模型可以通过交替方向乘子法（ADMM） 等现代优化算法高效求解。
✨第三部分：总结与展望------统一的视角
回顾SRC与ASRC的旅程，我们可以看到一个清晰的演进脉络：
-
SRC (
ℓ¹) ：确立了稀疏线性表示 作为分类核心的范式，其力量在于对遮挡的鲁棒性和清晰的几何解释。它位于"稀疏-协同"光谱的稀疏端。 -
ASRC (
Trace Norm) ：洞察到数据相关性结构 的重要性，通过迹范数这一数学工具，构建了一个数据驱动的、自适应 的正则化器。它不是一个固定的点，而是可以在"稀疏-协同"光谱上根据数据自由滑动的游标。
它们统一于一个更高的层面：都在寻求对测试样本 y 最本质、最具有判别性的线性表示 Xα。SRC定义了问题的起点和光谱的一端，而ASRC则提供了在这条光谱上智能导航的罗盘。