APS系统与OR-Tools完全指南：智能排产与优化算法实战解析

第一部分：APS系统概述与核心理论
- [🔍 什么是APS系统？](#🔍 什么是APS系统？)
- [🔍 APS系统的核心价值与技术特点](#🔍 APS系统的核心价值与技术特点)
- [📊 核心优化方法对比与MILP的应用](#📊 核心优化方法对比与MILP的应用)
- - [🧩 MILP的核心思想与在APS中的应用](#🧩 MILP的核心思想与在APS中的应用)
- [🔄 MILP的局限与其他高级算法](#🔄 MILP的局限与其他高级算法)
- [🔍 为何APS没有"通用解"：必须紧贴业务建模的核心原因](#🔍 为何APS没有“通用解”：必须紧贴业务建模的核心原因)
- [🛠️ 如何选择与实施APS](#🛠️ 如何选择与实施APS)
第二部分：APS中的甘特图与优化建模实践
- APS中的甘特图
- - [🧠 甘特图在APS中的核心作用](#🧠 甘特图在APS中的核心作用)
  - [📊 APS中甘特图的多样形式](#📊 APS中甘特图的多样形式)
- [🛠️ 优化建模技巧](#🛠️ 优化建模技巧)
- - [1. 减少不必要的变量](#1. 减少不必要的变量)
  - [2. 最小化变量的上下限](#2. 最小化变量的上下限)
  - [3. 一个约束一个约束的增加（迭代建模）](#3. 一个约束一个约束的增加（迭代建模）)
  - [4. 大型排程的小范围测试策略](#4. 大型排程的小范围测试策略)
  - [5. 结果验证与增量开发](#5. 结果验证与增量开发)
  - [6. 性能优化技巧](#6. 性能优化技巧)
  - [7. 调试与日志记录](#7. 调试与日志记录)
[第三部分：Google OR-Tools 完全指南：从求解器选型到实战应用](#第三部分：Google OR-Tools 完全指南：从求解器选型到实战应用)
- [🧭 概述](#🧭 概述)
- [📌 快速选择指南](#📌 快速选择指南)
- [🧩 核心求解器一览](#🧩 核心求解器一览)
- [🚀 快速开始](#🚀 快速开始)
- - [1. 安装](#1. 安装)
  - [2. 通用建模流程（四步法）](#2. 通用建模流程（四步法）)
- [📦 核心模块详解](#📦 核心模块详解)
- - pywraplp：线性规划/混合整数规划模块
  - - 支持的求解器后端
    - 常用方法示例
    - [`pywraplp` 求解器参数设置](#pywraplp 求解器参数设置)
  - CP-SAT：约束规划模块
  - - 核心建模方法
    - [CP-SAT 求解器参数](#CP-SAT 求解器参数)
  - CP-SAT日志输出说明
  - - [1. 求解启动部分](#1. 求解启动部分)
    - [2. 模型统计](#2. 模型统计)
    - [3. 预处理（Presolve）阶段](#3. 预处理（Presolve）阶段)
    - [4. 搜索过程关键术语](#4. 搜索过程关键术语)
    - [5. 边界改进](#5. 边界改进)
    - [6. 统计信息部分](#6. 统计信息部分)
    - [7. 求解结果](#7. 求解结果)
    - [8. 关键缩写含义](#8. 关键缩写含义)
  - 提供启发式初始解（MIPStart）
- [📊 求解结果解析](#📊 求解结果解析)
- - 求解状态说明
  - 获取求解统计信息
第四部分：实战应用、问题解决与学习资源
- [🚀 快速开始示例（生成计划排程）](#🚀 快速开始示例（生成计划排程）)
- [ortools运行报错：OSError: [WinError 127] 找不到指定的程序。](#ortools运行报错：OSError: [WinError 127] 找不到指定的程序。)
- - 两个解决方法
  - - [1. 安装 Microsoft Visual C++ Redistributable](#1. 安装 Microsoft Visual C++ Redistributable)
    - [2. 将ortools导入语句放在程序第一行](#2. 将ortools导入语句放在程序第一行)
- [📚 学习资源](#📚 学习资源)

第一部分：APS系统概述与核心理论

🔍 什么是APS系统？

生产计划是"方向"，生产排程是"执行"，而APS则是将二者智能融合、实现全局最优的"大脑"。

特征维度	生产计划	生产排程	高级计划与排程 (APS)
核心定义	为满足客户交付需求，对品种、数量、质量、进度的统筹安排。	在有限能力约束下，为具体生产任务分配资源、优化排序的过程。	集成了生产计划和生产排程的智能系统，通过优化算法，在全局范围内寻求最优解。
核心目标	面向交付，确保按时完工。	面向产出效率，优化设备、人员利用率。	平衡交付与效率，实现整体效益最大化。
时间维度	中长期 (如周、月、季)。	短期/实时 (如小时、天)，并需动态调整。	集成长短周期，实现一体化滚动计划与排程。
决策层次	战略/战术层，解决"做什么、做多少"。	作业执行层，解决"谁来做、何时做"。	协同优化层，连接战略与执行，实现闭环。
典型输出	主生产计划 (MPS)、需求计划。	详细的工序作业计划、派工单、甘特图。	经过同步优化、考虑多种约束的详细可执行计划。

🔍 APS系统的核心价值与技术特点

APS系统不仅仅是自动化工具，更是通过智能算法进行全局优化的决策支持系统。

核心价值 ：APS能在复杂的约束条件下，快速计算并模拟多种排产方案，从而提升订单准时交付率、优化资源利用率、降低在制品库存，最终增强企业应对市场波动的能力。
技术特点 ：其核心在于运用运筹优化算法 （如遗传算法、约束规划等）和模拟仿真技术，处理多工序、多资源、多目标的复杂优化问题。

📊 核心优化方法对比与MILP的应用

方法	全称	关键特征	在APS中的典型应用场景
LP	线性规划	变量连续，目标函数与约束条件均为线性。	资源（如原材料、连续产能）的连续优化分配，如炼油配方、化工生产流程优化。
IP	整数规划	变量全部为整数（如0, 1, 2）。是MILP的特例。	需要整数解的问题，如确定需要购买多少台整数的机器（不能买半台）。
MILP	混合整数线性规划	变量混合：部分连续（如产量）、部分整数（如是否生产）。	绝大部分复杂排程问题：设备启停（0/1决策）、批次划分（整数）、工序排序（使用0/1变量建模）。

🧩 MILP的核心思想与在APS中的应用

MILP之所以成为APS的"引擎"，是因为它能用数学模型精确描述生产中的离散选择 和连续决策，并寻找最优组合。

1. 核心建模思想

MILP通过引入 "0-1变量" 来建模"是/否"的决策。例如：

变量 x = 1 表示"在机器A上生产订单J"， x = 0 则表示"不生产"。
同时，用连续变量表示"生产多少"（如产量、时间）。
目标函数（如最小化成本、最大化效率）和所有约束（如产能、交货期）都必须是决策变量的线性表达式。

2. 在APS中的典型应用

MILP能直接对应解决APS中的核心难题：

设备分配与序列优化 ：为多个订单在多台机器上决定"在哪儿生产 "（0-1变量分配）和"按什么顺序生产"（用0-1变量定义先后顺序），以最小化完工时间或切换成本。
生产批量优化 ：决定将一个大的客户订单拆分成几个生产批次 （整数变量）以及每个批次的具体产量（连续变量），以平衡库存持有成本和设备切换成本。
人员班次计划 ：决定每天需要多少个班次 （整数变量）以及每个班次的具体人数或工作时长（连续变量），以满足生产需求并遵守劳动法规。

🔄 MILP的局限与其他高级算法

虽然强大，但MILP也有其局限。对于超大规模或实时性要求极高的问题，直接求解最优解可能耗时过长。因此，在实际的APS系统中，常会结合其他方法：

启发式与元启发式算法 （如遗传算法、模拟退火）：当问题过于复杂时，它们不求最优解，但能快速找到高质量的可行解，适用于动态实时排程。
约束规划 ：更擅长处理复杂的逻辑约束和序列约束（如"工序A必须比工序B早开始"），在复杂的作业车间排序问题中表现出色。

现代的APS系统通常是融合多种优化技术的混合求解器，根据问题特点选择或组合最合适的方法。

🔍 为何APS没有"通用解"：必须紧贴业务建模的核心原因

APS需要将企业独特的生产规则、资源、约束和目标，转化为可计算的数学模型，而这个"建模"过程是核心，也决定了其无法通用。

核心原因	具体说明
业务模式多样性	不同行业的工艺流程、瓶颈和优化目标完全不同（例如，PCB行业要解决复杂工序联动，而精细化工则更关注配方与批次优化）。
约束条件极其复杂	真实场景中充斥着多种约束的组合，如工艺顺序、设备切换、物料供给、人员技能、紧急插单等，这些非线性约束无法用一套标准逻辑处理。
优化目标个性化	不同企业甚至不同车间的核心目标都不同，有的是最短交期，有的是最高设备利用率，有的是最小换线成本，或这些目标的动态平衡。
问题本身是NP-Hard	多数生产排程问题在计算上属于 "NP-Hard"难题。这意味着随着问题规模扩大，几乎不可能在有限时间内找到理论最优解，必须结合业务经验设计启发式算法以获得可行解。

🛠️ 如何选择与实施APS

引入APS系统前，需要充分评估自身需求与管理基础：

评估现状 ：明确当前生产管理中的痛点（如交期不准、设备利用率低），并确保基础数据（如BOM、工艺路线、设备能力）的准确性。
明确目标：确定是优先解决交付问题、产能瓶颈还是库存问题。
选择策略 ：考虑系统是否与现有ERP、MES等系统有良好的集成能力，以及供应商的行业经验。
分步实施：建议从核心车间或产品线开始试点，验证效果后再逐步推广。

第二部分：APS中的甘特图与优化建模实践

APS中的甘特图

🧠 甘特图在APS中的核心作用

核心可视化与信息呈现

APS系统通过数学算法制定出精细到秒的排程方案，这些复杂的时间序列和逻辑关系，最终通过甘特图（Gantt Chart）进行图形化展示，让计划人员一目了然。这是其最基础也是最重要的作用。
动态交互与计划调整

当出现紧急插单、设备故障等突发状况时，计划员可以直接在甘特图上通过拖拽、分割等方式，直观、便捷地调整任务的顺序、时间或资源分配。系统会实时计算这种调整带来的连锁影响，辅助决策。
多维分析与决策支持

现代APS中的甘特图不止一种。通过切换不同的视图（如按资源、按订单、按负载），管理者可以从产能、订单进度、库存变化等多个维度审视生产全局，快速识别瓶颈或潜在风险，实现精细化管理。

📊 APS中甘特图的多样形式

甘特图类型	主要视角	呈现内容与作用	典型呈现
资源甘特图	设备/产线/班组	展示每一台设备、每一个班组在时间轴上的任务安排。用于检查设备利用率、避免冲突，是车间调度的核心视图。	横轴为时间，纵轴为设备列表，条形块为计划在该设备上执行的任务。
订单甘特图	客户订单/生产工单	追踪单个订单从第一道工序到最后完工的全过程。用于监控订单履约进度、预警延期风险。	横轴为时间，纵轴为订单列表，条形块显示该订单各工序的时间跨度及关联。
负载甘特图	资源负荷	直观显示各资源（设备、产线）的计划负载率（如满负荷、空闲、过载）。用于宏观把握产能平衡，为计划优化提供依据。	常以不同颜色（如红、黄、绿）或填充密度表示负载高低。

🛠️ 优化建模技巧

1. 减少不必要的变量

为什么重要 ：每个变量都会增加搜索空间维度，降低求解速度。
具体做法：

用已有变量表达式代替新变量
合并含义相似的变量
使用中间计算而非变量存储中间值
示例：如果只需要知道是否生产（0/1），就不要同时定义生产数量变量

2. 最小化变量的上下限

为什么重要 ：边界越紧，分支定界剪枝越有效。
具体做法：

根据业务逻辑收紧边界
动态计算可能范围
使用约束传播后的边界

3. 一个约束一个约束的增加（迭代建模）

为什么重要 ：便于调试，快速定位问题约束。
具体做法：

基础模型：只加核心约束，验证可行性
逐步增强：每次添加1-2个新约束类型
验证中间结果：每个阶段检查解的合理性

4. 大型排程的小范围测试策略

为什么重要 ：避免长时间运行后才发现模型错误。
具体做法：

时间切片：先排1天的计划，再扩展到1周
资源子集：先用10台机器测试，再扩展到100台
产品抽样：选5种代表性产品测试，再扩展到全部
参数简化：用简化业务规则验证逻辑

5. 结果验证与增量开发

具体做法：

完整性检查：解是否满足所有硬约束？
合理性检查：产能利用率、等待时间等指标是否合理？
边界测试：极值情况下的表现？
对比基准：与简单规则或历史方案对比

6. 性能优化技巧

高级策略：

对称性破除：对相同机器/产品添加顺序约束
松弛模型：先用连续松弛快速获得下界
启发式初始解：提供好的初始解加速求解
求解器参数调优：根据问题类型调整参数

7. 调试与日志记录

建议做法：

记录每次添加约束的影响
输出中间可行解的关键指标
使用求解器日志分析瓶颈

优化建模是迭代过程，不是一次性任务。从简单开始，逐步复杂化，持续验证，这是应对复杂排程问题的稳健策略。

第三部分：Google OR-Tools 完全指南：从求解器选型到实战应用

🧭 概述

Google OR-Tools 是一个开源的、专业的运筹学工具库，用于求解各类组合优化问题，如路径规划、资源分配、排班调度等。它内置了多种求解器，支持线性规划、约束规划、车辆路径规划等典型问题，并提供统一的 Python/C++/Java/.NET 接口。

📌 快速选择指南

问题特征	推荐求解器
所有关系都是线性关系	LP/MIP
包含复杂逻辑约束（如果...那么...、或、与等）	CP-SAT
需要规划车辆路线或配送方案	VRP
涉及网络流量或任务匹配	网络流/分配
变量大部分为整数且有复杂约束	CP-SAT
变量有连续值且关系简单	LP

🧩 核心求解器一览

求解器类型	主要模块/类	主要用途	典型应用场景	特点
线性/整数规划	`ortools.linear_solver`	在连续或整数变量的线性约束下，最大化或最小化线性目标	资源分配、生产计划、投资组合优化	处理连续/离散变量，核心是定义变量、约束和目标函数
约束规划 (CP-SAT)	`ortools.sat.python.cp_model`	处理涉及整数变量、布尔变量和复杂逻辑约束的问题	排班、调度、谜题、具有复杂业务规则的优化问题	表达复杂逻辑约束的能力强，支持非线性关系
车辆路径规划	`ortools.constraint_solver`	为车队规划最优路线，可处理时间窗、载重等现实约束	物流配送、外卖快递、垃圾收集路线规划、车辆调度	专为VRP设计，内置多种搜索策略和启发式算法
网络流与分配	`ortools.graph`	解决最大流、最小费用流、任务分配等问题	交通流量优化、人员任务指派、匹配问题、网络设计	高效的图算法实现，处理网络结构问题

🚀 快速开始

1. 安装

bash 复制代码

pip install ortools

2. 通用建模流程（四步法）

无论使用哪种求解器，基本建模流程相似：

创建求解器
选择合适的求解器后端（如 GLOP、SCIP、CP-SAT）。
定义变量
创建决策变量（连续、整数或布尔值）。
添加约束
用 Add() 方法添加问题的限制条件。
设置目标并求解
定义最大化或最小化的目标函数，调用 Solve()。

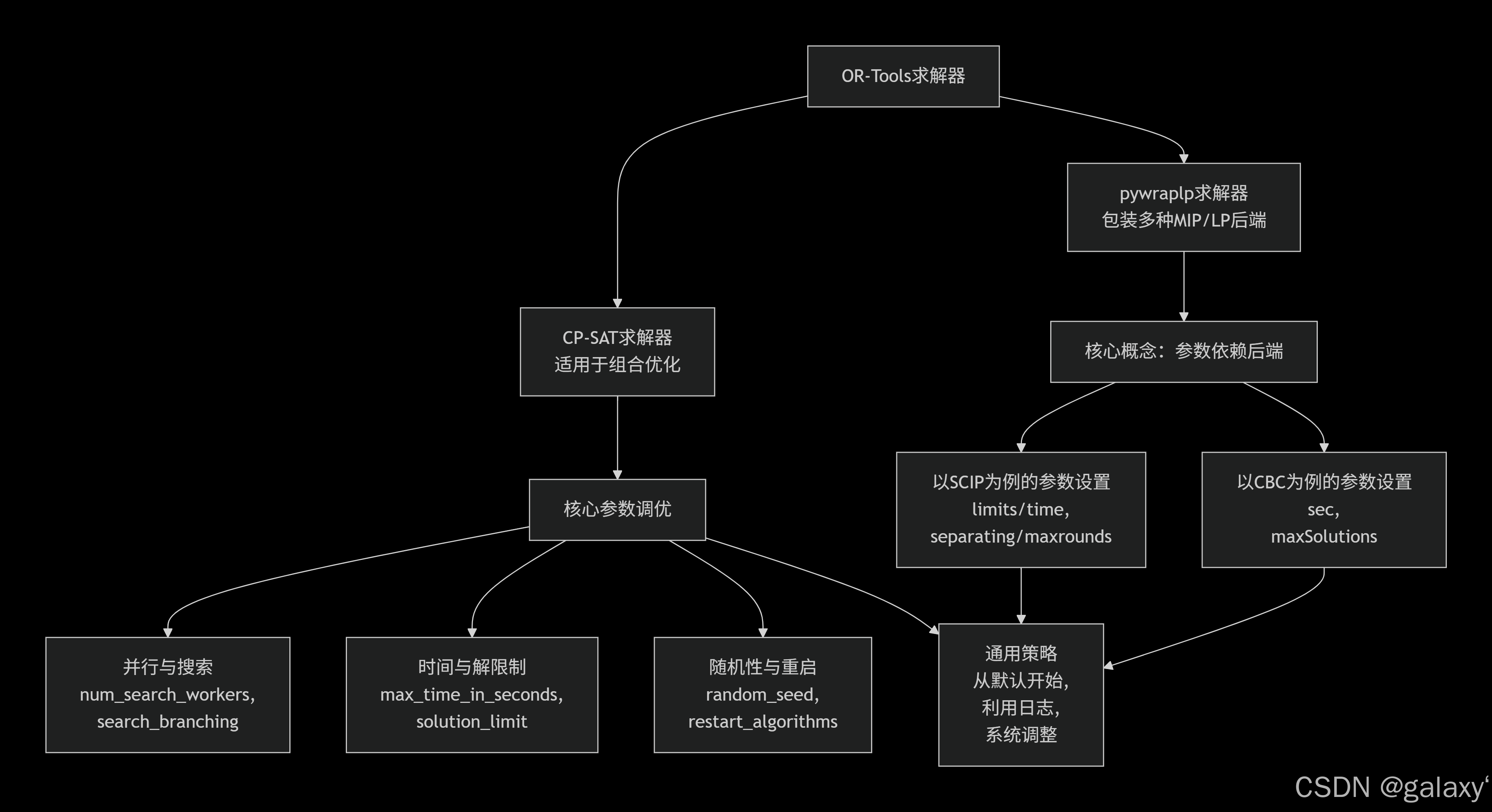
📦 核心模块详解

pywraplp：线性规划/混合整数规划模块

支持的求解器后端

求解器	类型	特点
GLOP	线性规划 (LP)	OR-Tools内置，免费，适用于纯线性规划
SCIP	混合整数规划 (MIP)	开源，支持整数变量，功能强大
CBC	混合整数规划 (MIP)	开源COIN-OR项目的一部分
GUROBI	商业求解器	高性能，需要许可证
CPLEX	商业求解器	IBM产品，业界领先
XPRESS	商业求解器	高性能优化器

常用方法示例

python 复制代码

from ortools.linear_solver import pywraplp

# 1. 声明求解器（指定后端，如SCIP）
solver = pywraplp.Solver.CreateSolver('SCIP')
if not solver:
    raise Exception('未找到指定的求解器')

# 2. 创建变量
x = solver.NumVar(0, solver.infinity(), 'x')  # 连续变量
y = solver.IntVar(0, 100, 'y')                # 整数变量
z = solver.BoolVar('z')                       # 0-1变量

# 3. 添加约束
solver.Add(2 * x + 3 * y <= 100)              # 线性约束
solver.Add(x >= 5 * z)                        # 含布尔变量的线性约束
solver.Add(x + y == 50)

# 4. 定义目标
solver.Maximize(5 * x + 8 * y + 2 * z)

# 5. 调用求解器
status = solver.Solve()

# 6. 处理结果
if status == pywraplp.Solver.OPTIMAL:
    print(f'x = {x.solution_value()}')       # 获取变量值
    print(f'y = {y.solution_value()}')
    print(f'最优目标值 = {solver.Objective().Value()}')
else:
    print('问题无最优解。')

`pywraplp` 求解器参数设置

pywraplp 提供了访问不同底层求解器（如 CBC、SCIP、GLOP 等）的接口，其参数主要通过以下方法设置：

通用方法（常用） ：使用 SetSolverSpecificParametersAsString 方法。此方法允许以字符串形式直接传递底层求解器的原生参数。
特定方法：部分通用参数（如时间限制）有独立的设置函数。

不同求解器的关键参数示例

参数类别	适用求解器	参数设置示例	说明
时间限制	所有求解器	`solver.SetTimeLimit(10000)` （单位：毫秒）	设置求解最大计算时间。
输出控制	CBC/SCIP	`solver.SetSolverSpecificParametersAsString("logLevel 1")`	`logLevel 0` 静默，`1` 常规输出，`2` 详细输出。
	GLOP	`solver.EnableOutput()`	GLOP 默认不输出，调用此函数开启基础日志。
最优间隙	CBC/SCIP	`solver.SetSolverSpecificParametersAsString("allowableGap 1e-5")`	当最优解与理论下界的相对间隙小于此值时，可提前停止。对求"足够好"的解很有用。
启发式策略	CBC	`solver.SetSolverSpecificParametersAsString("heuristics on maxNodes 100")`	开启启发式搜索并限制节点数，以在整数规划中更快找到可行解。
切割生成	CBC	`solver.SetSolverSpecificParametersAsString("gomory on cuts on passC 5")`	开启 Gomory 切割等，加强整数规划求解，但可能增加单次迭代时间。

CP-SAT：约束规划模块

CP-SAT 结合了约束规划（CP）和布尔可满足性问题（SAT），适用于具有复杂逻辑和整数约束的问题。

核心建模方法

python 复制代码

from ortools.sat.python import cp_model

# 1. 创建模型
model = cp_model.CpModel()

# 2. 创建变量
x = model.NewIntVar(0, 10, 'x')  # 整数变量，范围0-10
b = model.NewBoolVar('b')        # 布尔变量 (0或1)

# 3. 添加约束
model.Add(2 * x <= 11)                     # 线性约束
model.Add(x != 5)                          # 非线性约束（CP-SAT支持）
model.AddImplication(b, x == 7)            # 逻辑约束：如果b为True，则x必须等于7
model.AddAllDifferent([x, y, z])           # 全不同约束

# 处理乘积等非线性项（通过引入中间变量）
mult = model.NewIntVar(0, 100, 'mult')
model.AddMultiplicationEquality(mult, [x, y])  # 约束 mult == x * y

# 4. 定义目标
model.Maximize(x + 5)

# 5. 调用求解器
solver = cp_model.CpSolver()
# 可设置求解器参数，例如设置时间限制
solver.parameters.max_time_in_seconds = 30.0
status = solver.Solve(model)

# 6. 处理结果
if status in (cp_model.OPTIMAL, cp_model.FEASIBLE):
    print(f'x = {solver.Value(x)}')        # 获取变量值
    print(f'目标值 = {solver.ObjectiveValue()}')  # 获取目标值
else:
    print('未找到可行解。')

CP-SAT 求解器参数

CP-SAT 求解器参数主要通过 solver.parameters 进行设置。

设置方法示例：

python 复制代码

solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = 600
solver.parameters.absolute_gap_limit = 0.01

查看所有参数：

python 复制代码

print(str(solver.parameters))

主要参数分类说明

参数类别	参数名	类型	说明与典型取值
终止条件	`max_time_in_seconds`	`float`	最大求解时间（秒）。超时后停止，返回当前最优解。例如：`7200`。
	`max_number_of_conflicts`	`int`	最大冲突次数限制。冲突指导致回溯的赋值矛盾，用于控制搜索深度。
	`absolute_gap_limit`	`float`	绝对最优间隙。当 `当前解 - 最优下界 ≤` 此值时停止。
	`relative_gap_limit`	`float`	相对最优间隙。当 `(当前解 - 最优下界) / 最优下界 ≤` 此值时停止。
随机性控制	`random_seed`	`int`	随机种子。固定种子使结果可重现。例如：`42`。
	`randomize_search`	`bool`	随机化搜索。为 `True` 时在搜索中引入随机性，可能找到不同解。
并行求解	`num_search_workers`	`int`	并行工作线程数。通常设为 CPU 核心数。例如：`8`。
预处理	`cp_model_presolve`	`bool`	启用预处理。默认为 `True`，简化模型，通常能加速求解。
	`cp_model_probing_level`	`int`	探测级别。值越高，预处理时推理越强，但耗时可能增加。
启发式策略	`linearization_level`	`int`	线性化级别。值越高，尝试将约束线性化越多，影响求解策略。
	`use_objective_lb_search`	`bool`	基于目标下界的搜索。为 `True` 时，搜索更关注提升目标下界。
	`use_objective_ub_search`	`bool`	基于目标上界的搜索。为 `True` 时，搜索更关注降低目标上界（最小化问题）。
输出控制	`log_search_progress`	`bool`	输出进度日志。为 `True` 时在控制台输出求解信息。

CP-SAT日志输出说明

复制代码

Starting CP-SAT solver v9.14.6206
Parameters: max_time_in_seconds: 7200 log_search_progress: true num_search_workers: 8

Initial optimization model '': (model_fingerprint: 0x6af96e2f67ce2c37)
#Variables: 95'220 (#ints: 450 in floating point objective) (71'196 primary variables)
  - 64'314 Booleans in [0,1]
  - 186 different domains in [-1,100300] with a largest complexity of 1.
  - 184 constants in {0} 
#kIntProd: 12'960
#kLinear1: 102'497 (#enforced: 101'337)
#kLinear2: 86'297 (#enforced: 1'548) (#complex_domain: 630)
#kLinear3: 34'522
#kLinearN: 9'998 (#terms: 94'175)

Starting presolve at 0.18s
[Scaling] Floating point objective has 358 terms with magnitude in [1, 5] average = 3.41341
[Scaling] Objective coefficient relative error: 0
[Scaling] Objective worst-case absolute error: 0
[Scaling] Objective scaling factor: 1
  4.60e-02s  0.00e+00d  [DetectDominanceRelations] 
  4.07e-02s  0.00e+00d  [DetectDominanceRelations] 
  8.36e-01s  0.00e+00d  [operations_research::sat::CpModelPresolver::PresolveToFixPoint] #num_loops=10 #num_dual_strengthening=4 
  4.92e-03s  0.00e+00d  [operations_research::sat::CpModelPresolver::ExtractEncodingFromLinear] #potential_supersets=2'387 #potential_subsets=725 
  1.00e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDuplicateColumns] 
  1.85e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDuplicateConstraints] #duplicates=11'749 
[Symmetry] Graph for symmetry has 328'268 nodes and 617'678 arcs.
[Symmetry] Symmetry computation done. time: 0.257065 dtime: 0.310402
[Symmetry] #generators: 23, average support size: 4634.7
[Symmetry] 8134 orbits on 61433 variables with sizes: 8,8,8,8,8,8,8,8,8,8,...
[Symmetry] Num fixable by intersecting at_most_one with orbits: 8 largest_orbit: 8
[Symmetry] Found orbitope of size 3524 x 8
[SAT presolve] num removable Booleans: 4708 / 52280
[SAT presolve] num trivial clauses: 0
[SAT presolve] [0s] clauses:121487 literals:283471 vars:51260 one_side_vars:12617 simple_definition:10234 singleton_clauses:0
[SAT presolve] [0.0057348s] clauses:121346 literals:275125 vars:51260 one_side_vars:12659 simple_definition:10237 singleton_clauses:42
[SAT presolve] [0.013626s] clauses:103112 literals:234526 vars:46552 one_side_vars:12960 simple_definition:9702 singleton_clauses:21
  1.01e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDuplicateConstraintsWithDifferentEnforcements] 
  1.30e+00s  1.00e+00d *[operations_research::sat::CpModelPresolver::Probe] #probed=23'416 #fixed_bools=1'111 #new_bounds=1'600 #equiv=6'439 #new_binary_clauses=273'018 
  1.98e-01s  8.51e-01d  [MaxClique] Merged 76'293(166'339 literals) into 29'729(101'838 literals) at_most_ones. 
  3.75e-02s  0.00e+00d  [DetectDominanceRelations] 
  3.77e-02s  0.00e+00d  [DetectDominanceRelations] 
  3.37e-01s  0.00e+00d  [operations_research::sat::CpModelPresolver::PresolveToFixPoint] #num_loops=11 #num_dual_strengthening=4 
  2.41e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::ProcessAtMostOneAndLinear] #num_changes=5 
  1.12e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDuplicateConstraints] 
  1.20e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDuplicateConstraintsWithDifferentEnforcements] 
  9.14e-03s  2.53e-04d  [operations_research::sat::CpModelPresolver::DetectDominatedLinearConstraints] #relevant_constraints=7'526 #num_inclusions=1'252 #num_redundant=287 
  4.86e-03s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDifferentVariables] 
  2.58e-02s  8.21e-04d  [operations_research::sat::CpModelPresolver::ProcessSetPPC] #relevant_constraints=50'357 #num_inclusions=18'699 
  5.30e-03s  1.75e-04d  [operations_research::sat::CpModelPresolver::FindAlmostIdenticalLinearConstraints] #num_tested_pairs=1'268 #found=3 
  3.79e-02s  2.45e-02d  [operations_research::sat::CpModelPresolver::FindBigAtMostOneAndLinearOverlap] 
  1.40e-02s  4.87e-03d  [operations_research::sat::CpModelPresolver::FindBigVerticalLinearOverlap] #blocks=23 #saved_nz=9'036 
  8.42e-03s  4.46e-03d  [operations_research::sat::CpModelPresolver::FindBigHorizontalLinearOverlap] #linears=751 
  1.11e-02s  2.51e-04d  [operations_research::sat::CpModelPresolver::MergeClauses] 
  3.74e-02s  0.00e+00d  [DetectDominanceRelations] 
  3.45e-02s  0.00e+00d  [DetectDominanceRelations] 
  2.83e-01s  0.00e+00d  [operations_research::sat::CpModelPresolver::PresolveToFixPoint] #num_loops=9 #num_dual_strengthening=6 
  3.67e-02s  0.00e+00d  [DetectDominanceRelations] 
  3.26e-02s  0.00e+00d  [DetectDominanceRelations] 
  2.16e-01s  0.00e+00d  [operations_research::sat::CpModelPresolver::PresolveToFixPoint] #num_loops=7 #num_dual_strengthening=3 
  1.01e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDuplicateColumns] 
  1.02e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDuplicateConstraints] 
[Symmetry] Graph for symmetry has 239'083 nodes and 334'166 arcs.
[Symmetry] Symmetry computation done. time: 0.179755 dtime: 0.195098
[Symmetry] #generators: 28, average support size: 3206.29
[Symmetry] 6423 orbits on 51311 variables with sizes: 11,11,11,11,11,11,11,11,11,11,...
[Symmetry] Num fixable by intersecting at_most_one with orbits: 10 largest_orbit: 11
[Symmetry] Found orbitope of size 3119 x 8
[SAT presolve] num removable Booleans: 0 / 37681
[SAT presolve] num trivial clauses: 0
[SAT presolve] [0s] clauses:22907 literals:61897 vars:24197 one_side_vars:12341 simple_definition:11744 singleton_clauses:0
[SAT presolve] [0.0007639s] clauses:22907 literals:61897 vars:24197 one_side_vars:12341 simple_definition:11744 singleton_clauses:0
[SAT presolve] [0.00297s] clauses:22907 literals:61897 vars:24197 one_side_vars:12341 simple_definition:11744 singleton_clauses:0
  1.07e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDuplicateConstraintsWithDifferentEnforcements] 
  1.51e+00s  1.00e+00d *[operations_research::sat::CpModelPresolver::Probe] #probed=40'284 #fixed_bools=496 #new_bounds=75 #equiv=1'337 #new_binary_clauses=253'532 
  7.14e-02s  3.16e-01d  [MaxClique] Merged 8'427(36'405 literals) into 8'072(35'115 literals) at_most_ones. 
  3.89e-02s  0.00e+00d  [DetectDominanceRelations] 
  3.77e-02s  0.00e+00d  [DetectDominanceRelations] 
  2.69e-01s  0.00e+00d  [operations_research::sat::CpModelPresolver::PresolveToFixPoint] #num_loops=8 #num_dual_strengthening=3 
  2.21e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::ProcessAtMostOneAndLinear] 
  1.14e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDuplicateConstraints] #duplicates=3'915 
  1.16e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDuplicateConstraintsWithDifferentEnforcements] 
  6.84e-03s  1.51e-04d  [operations_research::sat::CpModelPresolver::DetectDominatedLinearConstraints] #relevant_constraints=7'067 #num_inclusions=787 #num_redundant=6 
  5.82e-03s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDifferentVariables] 
  1.70e-02s  4.92e-04d  [operations_research::sat::CpModelPresolver::ProcessSetPPC] #relevant_constraints=35'748 #num_inclusions=6'772 
  5.42e-03s  6.28e-05d  [operations_research::sat::CpModelPresolver::FindAlmostIdenticalLinearConstraints] #num_tested_pairs=621 #found=1 
  3.37e-02s  2.19e-02d  [operations_research::sat::CpModelPresolver::FindBigAtMostOneAndLinearOverlap] 
  1.19e-02s  4.01e-03d  [operations_research::sat::CpModelPresolver::FindBigVerticalLinearOverlap] #blocks=8 #saved_nz=3'079 
  9.79e-03s  4.57e-03d  [operations_research::sat::CpModelPresolver::FindBigHorizontalLinearOverlap] #linears=548 
  1.23e-02s  2.40e-04d  [operations_research::sat::CpModelPresolver::MergeClauses] 
  3.64e-02s  0.00e+00d  [DetectDominanceRelations] 
  3.95e-02s  0.00e+00d  [DetectDominanceRelations] 
  2.66e-01s  0.00e+00d  [operations_research::sat::CpModelPresolver::PresolveToFixPoint] #num_loops=6 #num_dual_strengthening=5 
  4.23e-02s  0.00e+00d  [DetectDominanceRelations] 
  3.86e-02s  0.00e+00d  [DetectDominanceRelations] 
  2.05e-01s  0.00e+00d  [operations_research::sat::CpModelPresolver::PresolveToFixPoint] #num_loops=2 #num_dual_strengthening=2 
  1.13e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDuplicateColumns] 
  1.03e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDuplicateConstraints] 
[Symmetry] Graph for symmetry has 229'551 nodes and 305'764 arcs.
[Symmetry] Symmetry computation done. time: 0.167589 dtime: 0.190074
[Symmetry] #generators: 404, average support size: 224.025
[Symmetry] 6321 orbits on 51274 variables with sizes: 216,108,36,18,18,18,18,18,18,18,...
[Symmetry] Num fixable by intersecting at_most_one with orbits: 11 largest_orbit: 216
[Symmetry] Found orbitope of size 3119 x 8
[SAT presolve] num removable Booleans: 0 / 35830
[SAT presolve] num trivial clauses: 0
[SAT presolve] [0s] clauses:23574 literals:63231 vars:24117 one_side_vars:11541 simple_definition:12464 singleton_clauses:0
[SAT presolve] [0.0008047s] clauses:23574 literals:63231 vars:24117 one_side_vars:11541 simple_definition:12464 singleton_clauses:0
[SAT presolve] [0.0028329s] clauses:23574 literals:63231 vars:24117 one_side_vars:11541 simple_definition:12464 singleton_clauses:0
  1.07e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDuplicateConstraintsWithDifferentEnforcements] 
  1.61e+00s  1.00e+00d *[operations_research::sat::CpModelPresolver::Probe] #probed=44'886 #new_bounds=1 #new_binary_clauses=223'145 
  6.16e-02s  2.73e-01d  [MaxClique] 
  4.20e-02s  0.00e+00d  [DetectDominanceRelations] 
  1.49e-01s  0.00e+00d  [operations_research::sat::CpModelPresolver::PresolveToFixPoint] #num_loops=2 #num_dual_strengthening=1 
  2.58e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::ProcessAtMostOneAndLinear] 
  1.19e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDuplicateConstraints] 
  1.03e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDuplicateConstraintsWithDifferentEnforcements] 
  6.63e-03s  1.15e-04d  [operations_research::sat::CpModelPresolver::DetectDominatedLinearConstraints] #relevant_constraints=7'045 #num_inclusions=671 
  5.06e-03s  0.00e+00d  [operations_research::sat::CpModelPresolver::DetectDifferentVariables] 
  1.66e-02s  4.92e-04d  [operations_research::sat::CpModelPresolver::ProcessSetPPC] #relevant_constraints=36'106 #num_inclusions=6'704 
  5.51e-03s  9.78e-06d  [operations_research::sat::CpModelPresolver::FindAlmostIdenticalLinearConstraints] #num_tested_pairs=329 
  3.02e-02s  1.88e-02d  [operations_research::sat::CpModelPresolver::FindBigAtMostOneAndLinearOverlap] 
  9.75e-03s  3.90e-03d  [operations_research::sat::CpModelPresolver::FindBigVerticalLinearOverlap] 
  6.93e-03s  4.55e-03d  [operations_research::sat::CpModelPresolver::FindBigHorizontalLinearOverlap] #linears=546 
  1.38e-02s  2.40e-04d  [operations_research::sat::CpModelPresolver::MergeClauses] 
  4.56e-02s  0.00e+00d  [DetectDominanceRelations] 
  1.65e-01s  0.00e+00d  [operations_research::sat::CpModelPresolver::PresolveToFixPoint] #num_loops=1 #num_dual_strengthening=1 
  2.31e-02s  0.00e+00d  [operations_research::sat::CpModelPresolver::ExpandObjective] #entries=580'116 #tight_variables=60'524 #tight_constraints=17'198 #expands=36 

Presolve summary:
  - 32982 affine relations were detected.
  - rule 'TODO domination: unexploited dominations' was applied 3 times.
  - rule 'TODO dual: add implied bound' was applied 20'880 times.
  - rule 'TODO dual: make linear1 equiv' was applied 464 times.
  - rule 'TODO dual: only one blocking constraint?' was applied 42'166 times.
  - rule 'TODO dual: only one blocking enforced constraint?' was applied 25'322 times.
  - rule 'TODO dual: only one unspecified blocking constraint?' was applied 78 times.
  - rule 'TODO dual: tighten at most one' was applied 29'063 times.
  - rule 'TODO linear inclusion: superset is equality' was applied 832 times.
  - rule 'TODO linear2: contains a Boolean.' was applied 141'090 times.
  - rule 'affine: new relation' was applied 32'982 times.
  - rule 'at_most_one: dominated singleton' was applied 107 times.
  - rule 'at_most_one: empty or all false' was applied 75 times.
  - rule 'at_most_one: removed literals' was applied 2'666 times.
  - rule 'at_most_one: resolved two constraints with opposite literal' was applied 1'068 times.
  - rule 'at_most_one: satisfied' was applied 16 times.
  - rule 'at_most_one: singleton' was applied 40 times.
  - rule 'at_most_one: size one' was applied 2'040 times.
  - rule 'at_most_one: transformed into max clique.' was applied 2 times.
  - rule 'at_most_one: x and not(x)' was applied 4 times.
  - rule 'bool_and: non-reified.' was applied 720 times.
  - rule 'bool_and: x => x' was applied 7'746 times.
  - rule 'bool_or: always true' was applied 741 times.
  - rule 'bool_or: implications' was applied 71'224 times.
  - rule 'bool_or: only one literal' was applied 2'386 times.
  - rule 'bool_or: removed enforcement literal' was applied 14'484 times.
  - rule 'deductions: 123179 stored' was applied 1 time.
  - rule 'deductions: reduced variable domain' was applied 5'040 times.
  - rule 'domination: added implications' was applied 1 time.
  - rule 'domination: fixed to lb.' was applied 32 times.
  - rule 'domination: reduced ub.' was applied 46 times.
  - rule 'dual: enforced equivalence' was applied 6'733 times.
  - rule 'dual: fix variable' was applied 30 times.
  - rule 'dual: make encoding equiv' was applied 126'208 times.
  - rule 'dual: reduced domain' was applied 741 times.
  - rule 'duplicate: removed constraint' was applied 15'664 times.
  - rule 'enforcement: false literal' was applied 13'948 times.
  - rule 'enforcement: true literal' was applied 3'659 times.
  - rule 'exactly_one: removed literals' was applied 1'408 times.
  - rule 'exactly_one: singleton' was applied 720 times.
  - rule 'exactly_one: size two' was applied 8 times.
  - rule 'exactly_one: x and not(x)' was applied 92 times.
  - rule 'int_prod: boolean affine term' was applied 12'960 times.
  - rule 'int_prod: reduced target domain.' was applied 720 times.
  - rule 'linear + amo: extracted enforcement literal' was applied 18 times.
  - rule 'linear + amo: fixed literal implied by enforcement' was applied 4 times.
  - rule 'linear + amo: trivial linear constraint' was applied 720 times.
  - rule 'linear inclusion: redundant included constraint' was applied 285 times.
  - rule 'linear inclusion: sparsify superset' was applied 4 times.
  - rule 'linear inclusion: subset + singleton is equality' was applied 4 times.
  - rule 'linear matrix: common vertical rectangle' was applied 31 times.
  - rule 'linear matrix: defining equation for common rectangle' was applied 4 times.
  - rule 'linear1: always true' was applied 740 times.
  - rule 'linear1: canonicalized' was applied 11 times.
  - rule 'linear1: transformed to implication' was applied 144 times.
  - rule 'linear1: x in domain' was applied 556 times.
  - rule 'linear2: contains a Boolean.' was applied 42 times.
  - rule 'linear: advanced affine relation from 2 constraints.' was applied 4 times.
  - rule 'linear: always true' was applied 30'165 times.
  - rule 'linear: coefficient strenghtening.' was applied 4 times.
  - rule 'linear: divide by GCD' was applied 5'735 times.
  - rule 'linear: doubleton free' was applied 138 times.
  - rule 'linear: empty' was applied 3'117 times.
  - rule 'linear: enforcement literal in expression' was applied 16'380 times.
  - rule 'linear: expanded complex rhs' was applied 128 times.
  - rule 'linear: extracted enforcement literal' was applied 22 times.
  - rule 'linear: fixed or dup variables' was applied 53'898 times.
  - rule 'linear: infeasible' was applied 2'354 times.
  - rule 'linear: negative clause' was applied 58'331 times.
  - rule 'linear: positive at most one' was applied 623 times.
  - rule 'linear: positive clause' was applied 38'792 times.
  - rule 'linear: positive equal one' was applied 970 times.
  - rule 'linear: reduced variable domains' was applied 6'251 times.
  - rule 'linear: reduced variable domains in derived constraint' was applied 101 times.
  - rule 'linear: remapped using affine relations' was applied 39'897 times.
  - rule 'linear: simplified rhs' was applied 1 time.
  - rule 'linear: singleton column' was applied 784 times.
  - rule 'linear: small Boolean expression' was applied 7'242 times.
  - rule 'linear: variable substitution 0' was applied 48 times.
  - rule 'linear: variable substitution 1' was applied 929 times.
  - rule 'linear: variable substitution 2' was applied 34 times.
  - rule 'new_bool: complex linear expansion' was applied 256 times.
  - rule 'new_bool: integer encoding' was applied 6'762 times.
  - rule 'objective: expanded via tight equality' was applied 36 times.
  - rule 'presolve: 9086 unused variables removed.' was applied 1 time.
  - rule 'presolve: iteration' was applied 3 times.
  - rule 'setppc: bool_or in at_most_one.' was applied 11'520 times.
  - rule 'setppc: removed dominated constraints' was applied 491 times.
  - rule 'variables: add encoding constraint' was applied 6'762 times.
  - rule 'variables: both boolean and its negation fix the same variable' was applied 8'345 times.
  - rule 'variables: canonicalize affine domain' was applied 1'897 times.
  - rule 'variables: canonicalize domain' was applied 5 times.
  - rule 'variables: detect fully reified value encoding' was applied 5'904 times.
  - rule 'variables: detect half reified value encoding' was applied 87'328 times.
  - rule 'variables: only used in encoding' was applied 1'102 times.

Presolved optimization model '': (model_fingerprint: 0xc5d6b7da898c4e48)
#Variables: 52'896 (#ints: 339 in objective) (41'381 primary variables)
  - 35'706 Booleans in [0,1]
  - 324 different domains in [-1,100300] with a largest complexity of 84.
#kAtMostOne: 714 (#literals: 20'709)
#kBoolAnd: 7'227 (#enforced: 7'227) (#literals: 14'832)
#kBoolOr: 16'097 (#literals: 48'405)
#kExactlyOne: 11'702 (#literals: 49'388)
#kLinear1: 36'585 (#enforced: 36'585 #multi: 7)
#kLinear2: 6'145 (#enforced: 5'697)
#kLinear3: 801 (#enforced: 720)
#kLinearN: 5'796 (#terms: 30'470)
[Symmetry] Graph for symmetry has 178'792 nodes and 306'532 arcs.
[Symmetry] Symmetry computation done. time: 0.176604 dtime: 0.186968
[Symmetry] #generators: 404, average support size: 225.134
[Symmetry] 6353 orbits on 51530 variables with sizes: 216,108,36,18,18,18,18,18,18,18,...
[Symmetry] Found orbitope of size 3135 x 8

Preloading model.
#Bound  10.18s best:inf   next:[33816,1381540] initial_domain
#Model  10.22s var:52896/52896 constraints:85067/85067 compo:52814,26,26,16,14

Starting search at 10.24s with 8 workers.
6 full problem subsolvers: [core, default_lp, max_lp_sym, no_lp, quick_restart, reduced_costs]
2 first solution subsolvers: [fj, fs_random_no_lp]
9 interleaved subsolvers: [feasibility_pump, graph_arc_lns, graph_cst_lns, graph_dec_lns, graph_var_lns, ls, rins/rens, rnd_cst_lns, rnd_var_lns]
3 helper subsolvers: [neighborhood_helper, synchronization_agent, update_gap_integral]

#1      13.32s best:969979 next:[33816,969978] fj_restart_decay_perturb(batch:1 lin{mvs:5'096 evals:41'034} #w_updates:167 #perturb:0)
#2      13.47s best:963818 next:[33816,963817] rnd_var_lns (d=5.00e-01 s=13 t=0.10 p=0.00 stall=0 h=base) [hint]
#3      13.60s best:961367 next:[33816,961366] rnd_cst_lns (d=5.00e-01 s=14 t=0.10 p=0.00 stall=0 h=base) [hint]
#4      13.71s best:960617 next:[33816,960616] graph_var_lns (d=5.00e-01 s=15 t=0.10 p=0.00 stall=0 h=base)
#5      13.71s best:958586 next:[33816,958585] graph_var_lns (d=5.00e-01 s=15 t=0.10 p=0.00 stall=0 h=base) [combined with: rnd_cst_lns (d=5.00e...]
#6      13.96s best:951446 next:[33816,951445] graph_cst_lns (d=5.00e-01 s=17 t=0.10 p=0.00 stall=0 h=base) [hint]
#7      14.04s best:931483 next:[33816,931482] graph_arc_lns (d=5.00e-01 s=16 t=0.10 p=0.00 stall=0 h=base)
#8      14.04s best:921562 next:[33816,921561] graph_arc_lns (d=5.00e-01 s=16 t=0.10 p=0.00 stall=0 h=base) [combined with: graph_cst_lns (d=5.0...]
#9      14.08s best:921559 next:[33816,921558] ls_restart_decay(batch:1 lin{mvs:40 evals:5'357} #w_updates:19 #perturb:0)
#10     14.08s best:921550 next:[33816,921549] ls_restart_decay_compound(batch:1 lin{mvs:0 evals:1'324} gen{mvs:19 evals:0} comp{mvs:7 btracks:6} #w_updates:0 #perturb:0)
#Bound  14.21s best:921550 next:[33837,921549] no_lp
#Bound  14.34s best:921550 next:[33842,921549] no_lp
#11     14.38s best:912825 next:[33842,912824] rnd_var_lns (d=7.07e-01 s=21 t=0.10 p=1.00 stall=0 h=base)
#Bound  14.39s best:912825 next:[34596,912824] quick_restart (initial_propagation)
#12     14.43s best:908406 next:[34596,908405] graph_dec_lns (d=7.07e-01 s=22 t=0.10 p=1.00 stall=1 h=base) [hint]
#13     14.45s best:908403 next:[34596,908402] ls_restart_perturb(batch:1 lin{mvs:12 evals:1'535} #w_updates:5 #perturb:0)
#Model  14.61s var:52680/52896 constraints:84633/85067 compo:52598,26,26,16,14
#Model  14.75s var:51592/52896 constraints:82446/85067 compo:51510,26,26,16,14
#Model  14.79s var:51360/52896 constraints:81961/85067 compo:51278,26,26,16,14
#Bound  14.79s best:908403 next:[50245,908402] quick_restart
#Model  14.94s var:50360/52896 constraints:79960/85067 compo:50278,26,26,16,14
#Model  15.08s var:49824/52896 constraints:78862/85067 compo:49742,26,26,16,14
#14     15.15s best:905040 next:[50245,905039] graph_var_lns (d=7.07e-01 s=25 t=0.10 p=1.00 stall=0 h=base)
#15     15.16s best:905037 next:[50245,905036] ls_restart_decay_compound_perturb(batch:1 lin{mvs:0 evals:1'129} gen{mvs:11 evals:0} comp{mvs:3 btracks:4} #w_updates:0 #perturb:0)
#16     15.17s best:905034 next:[50245,905033] ls_restart_decay(batch:1 lin{mvs:14 evals:2'021} #w_updates:6 #perturb:0)
#Bound  15.22s best:905034 next:[73486,905033] quick_restart
#17     15.36s best:894744 next:[73486,894743] graph_arc_lns (d=2.93e-01 s=29 t=0.10 p=0.00 stall=0 h=base)
#Bound  15.38s best:894744 next:[77996,894743] reduced_costs
#Bound  15.53s best:894744 next:[79296,894743] reduced_costs
#18     15.73s best:848033 next:[79296,848032] rnd_var_lns (d=8.14e-01 s=30 t=0.10 p=1.00 stall=0 h=base) [hint]
#19     15.74s best:848030 next:[79296,848029] ls_restart_decay(batch:1 lin{mvs:70 evals:6'967} #w_updates:35 #perturb:0)
#Bound  15.77s best:848030 next:[79860,848029] reduced_costs
#20     15.90s best:848029 next:[79860,848028] ls_restart_compound(batch:1 lin{mvs:0 evals:18'506} gen{mvs:162 evals:0} comp{mvs:12 btracks:75} #w_updates:1 #perturb:0)
#Bound  16.14s best:848029 next:[81062,848028] default_lp
#21     16.15s best:826761 next:[81062,826760] graph_arc_lns (d=1.86e-01 s=35 t=0.10 p=0.00 stall=0 h=base)
#Bound  16.26s best:826761 next:[92728,826760] max_lp_sym (initial_propagation)
#Model  16.30s var:49296/52896 constraints:77763/85067 compo:49214,26,26,16,14
#22     16.49s best:826758 next:[92728,826757] ls_restart(batch:1 lin{mvs:12 evals:1'696} #w_updates:5 #perturb:0)
#23     16.50s best:826755 next:[92728,826754] ls_restart_decay_perturb(batch:1 lin{mvs:11 evals:1'253} #w_updates:5 #perturb:0)
#24     16.70s best:821676 next:[92728,821675] graph_cst_lns (d=5.38e-01 s=41 t=0.10 p=0.50 stall=0 h=base) [hint]
#25     17.08s best:813639 next:[92728,813638] graph_arc_lns (d=1.24e-01 s=44 t=0.10 p=0.00 stall=0 h=base)
#26     17.09s best:813636 next:[92728,813635] ls_restart_decay_compound(batch:1 lin{mvs:0 evals:1'205} gen{mvs:15 evals:0} comp{mvs:5 btracks:5} #w_updates:0 #perturb:0)
#Bound  17.13s best:813636 next:[92941,813635] max_lp_sym
#27     17.40s best:810961 next:[92941,810960] rnd_var_lns (d=8.76e-01 s=43 t=0.10 p=1.00 stall=0 h=base) [hint]
#28     17.42s best:810951 next:[92941,810950] ls_restart_compound(batch:1 lin{mvs:0 evals:8'194} gen{mvs:137 evals:0} comp{mvs:7 btracks:65} #w_updates:1 #perturb:0)
#29     17.84s best:810279 next:[92941,810278] graph_dec_lns (d=7.21e-01 s=50 t=0.10 p=0.67 stall=0 h=base) [hint]
#30     18.02s best:809114 next:[92941,809113] graph_arc_lns (d=8.55e-02 s=52 t=0.10 p=0.00 stall=0 h=base)
#31     18.03s best:809111 next:[92941,809110] ls_restart_perturb(batch:1 lin{mvs:53 evals:4'916} #w_updates:33 #perturb:0)
#32     18.15s best:786812 next:[92941,786811] graph_cst_lns (d=6.92e-01 s=51 t=0.10 p=0.67 stall=0 h=base)
#33     18.15s best:785032 next:[92941,785031] graph_cst_lns (d=6.92e-01 s=51 t=0.10 p=0.67 stall=0 h=base) [combined with: ls_restart_perturb(b...]
#34     18.41s best:785029 next:[92941,785028] ls_restart_perturb(batch:1 lin{mvs:407 evals:44'477} #w_updates:232 #perturb:0)
#35     18.50s best:784855 next:[92941,784854] graph_arc_lns (d=8.37e-02 s=59 t=0.10 p=0.17 stall=1 h=base)
#36     18.51s best:784850 next:[92941,784849] ls_restart_perturb(batch:1 lin{mvs:7 evals:738} #w_updates:3 #perturb:0)
#37     18.54s best:784528 next:[92941,784527] graph_var_lns (d=3.59e-01 s=57 t=0.10 p=0.33 stall=1 h=base)
#38     18.55s best:784346 next:[92941,784345] graph_var_lns (d=3.59e-01 s=57 t=0.10 p=0.33 stall=1 h=base) [combined with: ls_restart_perturb(b...]
#39     18.68s best:776279 next:[92941,776278] graph_arc_lns (d=1.13e-01 s=61 t=0.10 p=0.29 stall=0 h=base)
#40     18.69s best:775775 next:[92941,775774] graph_arc_lns (d=1.13e-01 s=61 t=0.10 p=0.29 stall=0 h=base) [combined with: graph_var_lns (d=3.5...]
#41     18.69s best:775772 next:[92941,775771] ls_restart_compound(batch:1 lin{mvs:0 evals:2'659} gen{mvs:32 evals:0} comp{mvs:6 btracks:13} #w_updates:0 #perturb:0)
#42     18.71s best:775577 next:[92941,775576] graph_var_lns (d=2.48e-01 s=62 t=0.10 p=0.25 stall=0 h=base) [combined with: ls_restart_compound(...]
#43     18.93s best:775392 next:[92941,775391] graph_dec_lns (d=5.97e-01 s=64 t=0.10 p=0.50 stall=0 h=base) [hint] [combined with: graph_var_lns (d=2.4...]
#44     19.05s best:763896 next:[92941,763895] graph_arc_lns (d=8.50e-02 s=67 t=0.10 p=0.25 stall=0 h=base)
#45     19.07s best:763893 next:[92941,763892] ls_restart(batch:1 lin{mvs:38 evals:4'670} #w_updates:18 #perturb:0)
#Bound  19.10s best:763893 next:[93698,763892] max_lp_sym
#46     19.21s best:762633 next:[93698,762632] graph_var_lns (d=1.76e-01 s=69 t=0.10 p=0.20 stall=0 h=base)
#47     19.61s best:761169 next:[93698,761168] graph_cst_lns (d=5.54e-01 s=71 t=0.10 p=0.50 stall=0 h=base)
#48     19.62s best:761166 next:[93698,761165] ls_restart_perturb(batch:1 lin{mvs:14 evals:2'052} #w_updates:6 #perturb:0)
#49     19.65s best:761064 next:[93698,761063] graph_arc_lns (d=1.12e-01 s=73 t=0.10 p=0.33 stall=0 h=base)
#50     19.78s best:754305 next:[93698,754304] rnd_var_lns (d=8.21e-01 s=70 t=0.10 p=0.75 stall=0 h=base) [hint]
#Bound  19.81s best:754305 next:[93757,754304] max_lp_sym
#51     20.16s best:750242 next:[93757,750241] graph_dec_lns (d=7.14e-01 s=76 t=0.10 p=0.60 stall=0 h=base) [hint]
#52     20.17s best:750239 next:[93757,750238] ls_restart_decay(batch:1 lin{mvs:7 evals:908} #w_updates:3 #perturb:0)
#53     20.17s best:749166 next:[93757,749165] graph_var_lns (d=1.28e-01 s=77 t=0.10 p=0.17 stall=0 h=base)
#54     20.17s best:745100 next:[93757,745099] graph_var_lns (d=1.28e-01 s=77 t=0.10 p=0.17 stall=0 h=base) [combined with: ls_restart_decay(bat...]
#55     20.18s best:745095 next:[93757,745094] ls_restart_decay_compound_perturb(batch:1 lin{mvs:0 evals:17'188} gen{mvs:229 evals:0} comp{mvs:25 btracks:102} #w_updates:4 #perturb:0)
#56     20.41s best:745090 next:[93757,745089] graph_var_lns (d=9.44e-02 s=82 t=0.10 p=0.14 stall=0 h=base)
#57     20.59s best:744544 next:[93757,744543] graph_var_lns (d=1.26e-01 s=83 t=0.10 p=0.25 stall=0 h=base)
#58     20.75s best:744539 next:[93757,744538] ls_restart(batch:1 lin{mvs:29 evals:3'302} #w_updates:14 #perturb:0)
#59     20.95s best:741422 next:[93757,741421] graph_arc_lns (d=8.84e-02 s=87 t=0.10 p=0.33 stall=1 h=base)
#60     20.96s best:741412 next:[93757,741411] ls_restart_decay(batch:1 lin{mvs:73 evals:8'463} #w_updates:36 #perturb:0)
#Bound  21.08s best:741412 next:[93968,741411] max_lp_sym
#61     21.45s best:739766 next:[93968,739765] graph_dec_lns (d=7.92e-01 s=89 t=0.10 p=0.67 stall=0 h=base) [hint]
#Bound  21.66s best:739766 next:[94010,739765] max_lp_sym
#62     21.71s best:739741 next:[94010,739740] ls_restart_compound_perturb(batch:1 lin{mvs:0 evals:7'357} gen{mvs:120 evals:0} comp{mvs:22 btracks:49} #w_updates:1 #perturb:0)
#63     21.85s best:739546 next:[94010,739545] graph_arc_lns (d=6.98e-02 s=96 t=0.10 p=0.31 stall=0 h=base)
#64     21.92s best:739541 next:[94010,739540] ls_restart_compound(batch:1 lin{mvs:0 evals:1'257} gen{mvs:18 evals:0} comp{mvs:6 btracks:6} #w_updates:0 #perturb:0)
#65     22.06s best:738521 next:[94010,738520] graph_var_lns (d=7.34e-02 s=99 t=0.10 p=0.20 stall=1 h=base)
#66     22.09s best:738425 next:[94010,738424] graph_arc_lns (d=1.10e-01 s=100 t=0.10 p=0.40 stall=1 h=base)
......
......
......
......
......
#818   2201.45s best:97526 next:[94885,97525] graph_var_lns (d=4.59e-01 s=13162 t=0.10 p=0.50 stall=6 h=base) [combined with: ls_restart_perturb(b...]
#819   2201.46s best:97521 next:[94885,97520] ls_restart(batch:1 lin{mvs:114 evals:4'399} #w_updates:61 #perturb:0)
#820   2201.94s best:97425 next:[94885,97424] graph_arc_lns (d=5.19e-01 s=13168 t=0.10 p=0.51 stall=6 h=base) [hint]
#821   2201.95s best:97420 next:[94885,97419] ls_restart(batch:1 lin{mvs:136 evals:4'408} #w_updates:81 #perturb:0)
#822   2202.32s best:95757 next:[94885,95756] graph_arc_lns (d=5.19e-01 s=13169 t=0.10 p=0.51 stall=6 h=base)
#823   2202.34s best:95754 next:[94885,95753] ls_restart_compound(batch:1 lin{mvs:0 evals:4'934} gen{mvs:282 evals:0} comp{mvs:18 btracks:132} #w_updates:3 #perturb:0)
#824   2203.05s best:95720 next:[94885,95719] rnd_var_lns (d=7.94e-01 s=13175 t=0.10 p=0.50 stall=0 h=base) [hint]
#825   2203.51s best:95715 next:[94885,95714] rnd_var_lns (d=7.94e-01 s=13176 t=0.10 p=0.50 stall=0 h=base)
#826   2204.01s best:95712 next:[94885,95711] rnd_cst_lns (d=8.35e-01 s=13177 t=0.10 p=0.50 stall=8 h=base) [hint] [combined with: rnd_var_lns (d=7.94e...]
#Bound 2214.80s best:95712 next:[94922,95711] max_lp_sym
#Model 2214.86s var:48951/52896 constraints:77389/85067 compo:48770,26,26,26,23,22,16,14,11,10,...
#Model 2220.89s var:48950/52896 constraints:77375/85067 compo:48742,27,26,26,26,23,22,16,14,11,...
#827   2226.96s best:94974 next:[94922,94973] rins_lp_lns (d=2.15e-01 s=13313 t=0.11 p=0.51 stall=2 h=base)
#Model 2227.64s var:48949/52896 constraints:77369/85067 compo:48715,27,26,26,26,26,23,22,16,14,...
#Model 2230.21s var:48226/52896 constraints:76992/85067 compo:47859,27,27,27,27,26,26,26,26,26,...
#Model 2230.60s var:48210/52896 constraints:76959/85067 compo:47843,27,27,27,27,26,26,26,26,26,...
#Model 2231.19s var:48194/52896 constraints:76927/85067 compo:47827,27,27,27,27,26,26,26,26,26,...
#Model 2234.28s var:48107/52896 constraints:76789/85067 compo:47718,27,27,27,27,26,26,26,26,26,...
#Model 2236.55s var:48106/52896 constraints:76777/85067 compo:47690,27,27,27,27,27,26,26,26,26,...
#Model 2241.03s var:48080/52896 constraints:76719/85067 compo:47664,27,27,27,27,27,26,26,26,26,...
#Model 2241.22s var:48026/52896 constraints:76701/85067 compo:47610,27,27,27,27,27,26,26,26,26,...
#Model 2243.26s var:47999/52896 constraints:76688/85067 compo:47583,27,27,27,27,27,26,26,26,26,...
#Bound 2243.46s best:94974 next:[94933,94973] max_lp_sym
#Model 2243.52s var:47972/52896 constraints:76675/85067 compo:47556,27,27,27,27,27,26,26,26,26,...
#Done  2249.76s max_lp_sym

Task timing                   n [     min,      max]      avg      dev     time         n [     min,      max]      avg      dev    dtime
              'core':         1 [  37.33m,   37.33m]   37.33m   0.00ns   37.33m         1 [  12.37m,   12.37m]   12.37m   0.00ns   12.37m
        'default_lp':         1 [  37.33m,   37.33m]   37.33m   0.00ns   37.33m         1 [   5.14m,    5.14m]    5.14m   0.00ns    5.14m
  'feasibility_pump':       303 [253.79ms,    3.20s]    1.66s 298.24ms    8.39m       302 [390.01ms,    1.49s] 522.32ms  78.04ms    2.63m
                'fj':         4 [ 22.64ms, 175.44ms] 105.78ms  54.48ms 423.11ms         4 [ 12.55ms, 100.63ms]  78.37ms  38.00ms 313.48ms
   'fs_random_no_lp':         1 [   3.14s,    3.14s]    3.14s   0.00ns    3.14s         0 [  0.00ns,   0.00ns]   0.00ns   0.00ns   0.00ns
     'graph_arc_lns':      1375 [ 25.10ms,    1.84s] 365.62ms 235.46ms    8.38m      1375 [ 10.00ns, 100.29ms]  53.63ms  48.33ms    1.23m
     'graph_cst_lns':       678 [150.35ms,    1.94s] 741.77ms 213.23ms    8.38m       678 [110.83us, 100.48ms]  55.84ms  46.22ms   37.86s
     'graph_dec_lns':       570 [124.44ms,    1.81s] 885.13ms 224.45ms    8.41m       570 [ 10.00ns, 100.20ms]  57.24ms  46.09ms   32.63s
     'graph_var_lns':      1787 [ 25.35ms,    1.17s] 282.03ms 165.63ms    8.40m      1787 [ 10.00ns, 102.20ms]  54.08ms  47.93ms    1.61m
                'ls':      5024 [  6.66ms, 192.15ms]  88.94ms  28.29ms    7.45m      5024 [ 24.24us, 100.26ms]  92.75ms  25.27ms    7.77m
        'max_lp_sym':         1 [  37.33m,   37.33m]   37.33m   0.00ns   37.33m         1 [   5.49m,    5.49m]    5.49m   0.00ns    5.49m
             'no_lp':         1 [  37.33m,   37.33m]   37.33m   0.00ns   37.33m         1 [  19.34m,   19.34m]   19.34m   0.00ns   19.34m
     'quick_restart':         1 [  37.33m,   37.33m]   37.33m   0.00ns   37.33m         1 [   5.27m,    5.27m]    5.27m   0.00ns    5.27m
     'reduced_costs':         1 [  37.33m,   37.33m]   37.33m   0.00ns   37.33m         1 [  15.18m,   15.18m]   15.18m   0.00ns   15.18m
         'rins/rens':      2373 [  4.02ms, 829.39ms] 211.72ms 212.20ms    8.37m      1869 [ 10.00ns, 106.39ms]  51.59ms  52.11ms    1.61m
       'rnd_cst_lns':       556 [185.04ms,    1.92s] 905.72ms 223.70ms    8.39m       556 [  2.62us, 101.12ms]  56.77ms  46.00ms   31.57s
       'rnd_var_lns':       784 [157.89ms,    4.01s] 641.62ms 264.59ms    8.38m       784 [ 19.29us, 100.83ms]  54.87ms  47.27ms   43.02s

Search stats            Bools  Conflicts     Branches   Restarts     BoolPropag  IntegerPropag
             'core':  110'435    753'348  111'254'147     21'098  4'749'094'738  2'887'819'388
       'default_lp':   65'212     37'142    2'657'773    265'094    313'637'174    271'864'792
  'fs_random_no_lp':   63'971          0       17'530     17'530      5'010'457      5'101'040
       'max_lp_sym':   69'076     17'581    1'379'254    163'315    165'286'338    362'092'564
            'no_lp':   80'035  4'103'715   70'599'098  1'028'006  4'050'567'799  5'580'267'945
    'quick_restart':   67'825     12'137    2'757'554    294'178    306'422'641    262'537'168
    'reduced_costs':   67'758     19'604    1'749'734    237'966    208'893'010    243'888'521

SAT stats             ClassicMinim  LitRemoved   LitLearned  LitForgotten  Subsumed  MClauses  MDecisions  MLitTrue  MSubsumed  MLitRemoved  MReused
             'core':       592'892   1'434'496   12'295'776    11'892'361     2'814         0           0         0          0            0        0
       'default_lp':        22'333     300'692    4'182'520     1'202'297       530   240'592     576'268         5      9'935       63'009   91'434
  'fs_random_no_lp':             0           0            0             0         0         0           0         0          0            0        0
       'max_lp_sym':        10'393     371'138    2'820'474     1'320'330       122   133'628     319'787        20      7'631       44'508   54'525
            'no_lp':     3'207'348  34'777'236  175'178'448   171'582'405     7'914   846'298   1'905'536        14     25'590      139'452  481'246
    'quick_restart':         5'189      51'824      734'642             0       118   283'011     646'410         2      8'280       40'946  112'617
    'reduced_costs':        14'940     254'259    2'573'611        77'442       172   204'679     450'965         1      7'292       29'901   84'862

Lp stats            Component  Iterations  AddedCuts    OPTIMAL  DUAL_F.  DUAL_U.
     'default_lp':      5'045   1'983'275     29'340  2'248'305      232    1'181
     'max_lp_sym':          5   1'369'556     64'489     81'050  111'959      893
  'quick_restart':      5'045   1'731'563     38'548  3'130'468      245    1'247
  'reduced_costs':          5   1'834'118     88'155     30'053  178'209    1'019

Lp dimension              Final dimension of first component
     'default_lp':              0 rows, 4 columns, 0 entries
     'max_lp_sym':    6004 rows, 7637 columns, 47279 entries
  'quick_restart':              0 rows, 4 columns, 0 entries
  'reduced_costs':  21467 rows, 52814 columns, 85281 entries

Lp debug            CutPropag  CutEqPropag   Adjust  Overflow        Bad  BadScaling
     'default_lp':        462          685  277'510         0    360'189           0
     'max_lp_sym':        904        1'973  172'534         0  1'150'590           0
  'quick_restart':        568        1'307  233'274         0    603'866           0
  'reduced_costs':        173            7  202'922         0    436'350           0

Lp pool             Constraints  Updates  Simplif  Merged  Shortened   Split  Strenghtened         Cuts/Call
     'default_lp':       21'433    3'571   68'631      78      3'143  13'179        22'864    29'340/113'384
     'max_lp_sym':       24'454   13'783  344'323     102     10'414  21'661         5'681  64'489/1'719'696
  'quick_restart':       21'635    7'893   89'749      84     12'723  31'192        27'875    38'548/120'671
  'reduced_costs':      121'636      624  768'606      20     11'036   4'655        19'313    88'155/255'946

Lp Cut            max_lp_sym  default_lp  quick_restart  reduced_costs
          CG_FF:         650       1'678          2'517            280
           CG_K:         698       1'840          2'682            286
          CG_KL:           -           -              1             65
           CG_R:       1'520       2'343          4'398            318
          CG_RB:         452         863          1'780            221
         CG_RBP:         333         302            606             80
         Clique:       1'126           -              -            627
             IB:      35'880       6'847          6'058         52'486
       MIR_1_FF:         211         521            651          1'740
        MIR_1_K:         194         353            461          1'407
       MIR_1_KL:           -          25             12            324
        MIR_1_R:         236         336            486             99
       MIR_1_RB:         137         444            527            578
      MIR_1_RBP:          61          57             77            201
      MIR_1_RLT:           -           -              -          1'685
       MIR_2_FF:       1'407         979          1'159          1'474
        MIR_2_K:         923         541            654          1'313
       MIR_2_KL:           -          24              5            363
        MIR_2_R:       1'180         583            958            396
       MIR_2_RB:         570         462            565          1'300
      MIR_2_RBP:         351          67            103            425
       MIR_3_FF:       1'293         790          1'117          1'853
        MIR_3_K:       1'011         400            635          1'319
       MIR_3_KL:           -           4              3            420
        MIR_3_R:       1'576         614          1'129            563
       MIR_3_RB:         609         417            532          1'349
      MIR_3_RBP:         322          49            101            512
       MIR_4_FF:         850         759          1'094          1'899
        MIR_4_K:         738         368            481            970
       MIR_4_KL:           -           2              -            255
        MIR_4_R:       1'646         613            995            611
       MIR_4_RB:         521         332            392          1'543
      MIR_4_RBP:         289          31             81            480
       MIR_5_FF:         756         790          1'002          1'235
        MIR_5_K:         664         343            406            695
       MIR_5_KL:           -           -              1            109
        MIR_5_R:       1'793         763            934            590
       MIR_5_RB:         638         297            353          1'148
      MIR_5_RBP:         387          37             46            459
       MIR_6_FF:         449         884            999            902
        MIR_6_K:         454         406            453            548
       MIR_6_KL:           -           -              -             67
        MIR_6_R:       1'919         839          1'020            544
       MIR_6_RB:         600         459            464            887
      MIR_6_RBP:         366          36             55            451
   ZERO_HALF_FF:          78         119            188            573
    ZERO_HALF_K:          66         115            118            404
   ZERO_HALF_KL:           -           1              1            124
    ZERO_HALF_R:       1'368       1'431          2'005          1'003
   ZERO_HALF_RB:          73         164            211            708
  ZERO_HALF_RBP:          94          12             32            266

LNS stats           Improv/Calls  Closed  Difficulty  TimeLimit
  'graph_arc_lns':      136/1375     51%    5.68e-01       0.10
  'graph_cst_lns':        98/678     50%    7.55e-01       0.10
  'graph_dec_lns':        85/570     50%    8.51e-01       0.10
  'graph_var_lns':      170/1787     51%    6.51e-01       0.10
      'rins/rens':      723/1875     51%    2.58e-01       0.11
    'rnd_cst_lns':        81/556     51%    8.66e-01       0.10
    'rnd_var_lns':       115/784     51%    8.27e-01       0.10

LS stats                                Batches  Restarts/Perturbs    LinMoves   GenMoves  CompoundMoves  Bactracks  WeightUpdates  ScoreComputed
                         'fj_restart':        1                  1      17'744          0              0          0         63'516        749'363
            'fj_restart_compound_obj':        1                  1           0     49'290          8'864     20'202             40        502'170
           'fj_restart_decay_perturb':        2                  2      43'493          0              0          0            548        297'287
                         'ls_restart':      727                390  15'864'667          0              0          0      8'082'656    511'977'569
                'ls_restart_compound':      615                360           0  8'347'779        510'724  3'917'889         88'163    392'989'717
        'ls_restart_compound_perturb':      649                381           0  8'999'903        557'453  4'220'480         94'337    420'079'707
                   'ls_restart_decay':      648                368  17'845'326          0              0          0        150'832    251'987'308
          'ls_restart_decay_compound':      657                346           0  7'912'630      1'159'575  3'374'874         16'553    406'971'274
  'ls_restart_decay_compound_perturb':      552                360           0  6'173'349        899'184  2'635'373         15'774    346'628'802
           'ls_restart_decay_perturb':      558                362  14'771'518          0              0          0        144'266    226'190'321
                 'ls_restart_perturb':      618                353  13'294'053          0              0          0      7'397'471    436'428'226

Solutions (827)                         Num       Rank
                         'default_lp':   15  [354,810]
           'fj_restart_decay_perturb':    1      [1,1]
                      'graph_arc_lns':   78    [7,822]
                      'graph_cst_lns':   61    [6,808]
                      'graph_dec_lns':   42   [12,771]
                      'graph_var_lns':   93    [4,818]
                         'ls_restart':   59   [22,821]
                'ls_restart_compound':   70   [20,823]
        'ls_restart_compound_perturb':   62   [62,813]
                   'ls_restart_decay':   28    [9,811]
          'ls_restart_decay_compound':   48   [10,779]
  'ls_restart_decay_compound_perturb':   50   [15,816]
           'ls_restart_decay_perturb':   25   [23,814]
                 'ls_restart_perturb':   49   [13,817]
                         'max_lp_sym':    1  [509,509]
                      'rens_pump_lns':    1  [156,156]
                        'rins_lp_lns':   27   [75,827]
                      'rins_pump_lns':    3  [357,803]
                        'rnd_cst_lns':   39    [3,826]
                        'rnd_var_lns':   75    [2,825]

Objective bounds     Num
      'default_lp':    1
  'initial_domain':    1
      'max_lp_sym':   34
           'no_lp':    2
   'quick_restart':    3
   'reduced_costs':    3

Solution repositories    Added  Queried  Synchro
  'feasible solutions':  6'264   20'929    4'030
   'fj solution hints':      0        0        0
        'lp solutions':  7'541    1'380    6'531
                'pump':  1'776      993

Improving bounds shared      Num  Sym
                  'core':     56    0
            'default_lp':  1'179    0
            'max_lp_sym':  3'236  718
                 'no_lp':  3'304  487
         'quick_restart':  1'821  267
         'reduced_costs':    216  308

Clauses shared         Num
           'core':      50
     'default_lp':  35'163
     'max_lp_sym':   4'883
          'no_lp':  42'703
  'quick_restart':  13'171
  'reduced_costs':  26'770

CpSolverResponse summary:
status: OPTIMAL
objective: 94974
best_bound: 94974
integers: 30912
booleans: 63971
conflicts: 0
branches: 17530
propagations: 5010457
integer_propagations: 5101040
restarts: 17530
lp_iterations: 0
walltime: 2251.24
usertime: 2251.24
deterministic_time: 4808.1
gap_integral: 12114.5
solution_fingerprint: 0xf6bece014f5e0712

1. 求解启动部分

CP-SAT solver v9.14.6206：约束规划与布尔可满足性求解器版本
max_time_in_seconds: 7200：最大求解时间2小时
log_search_progress: true：记录搜索进度
num_search_workers: 8：使用8个工作线程并行求解

2. 模型统计

#Variables: 95'220：95,220个变量（其中64,314个布尔变量）
#kLinearN：线性约束数量
model_fingerprint：模型指纹（用于标识）

3. 预处理（Presolve）阶段

DetectDominanceRelations：检测支配关系
DetectDuplicateConstraints：检测重复约束
Symmetry computation：对称性计算（找出对称变量组）
orbitope：轨道结构（对称群作用下的变量结构）
Probe：探针技术（试探性赋值以简化问题）
Fixed bools：固定的布尔变量数量
Affine relations：仿射关系（线性关系）

4. 搜索过程关键术语

best:inf：当前最优解为无穷大（初始）
fj (first job)：首次找到可行解的启发式方法
rnd_var_lns：基于随机变量的Large Neighborhood Search（大邻域搜索）
graph_arc_lns：基于图弧的LNS
ls (local search)：局部搜索
rins/rens：RINS/RENS启发式（基于LP解的舍入）
feasibility_pump：可行性泵
d=5.00e-01：破坏率50%
s=13：第13个搜索步骤
stall=0：停滞次数
[hint]：使用先前解的提示
combined with：多种搜索策略组合

5. 边界改进

Bound：下界更新
next:[33816,1381540]：下一个边界区间[下界, 上界]

6. 统计信息部分

任务计时（Task timing）

time：实际时间
dtime：确定性时间（与问题复杂度相关）

搜索统计（Search stats）

Bools：布尔变量数量
Conflicts：冲突次数
Branches：分支次数
Restarts：重启次数
BoolPropag：布尔传播次数
IntegerPropag：整数传播次数

SAT统计

ClassicMinim：经典最小化
LitRemoved：删除的文字数
LitLearned：学习的文字数
Subsumed：子句吸收

LP统计

Iterations：迭代次数
AddedCuts：添加的割平面
OPTIMAL/DUAL_F/DUAL_U：LP求解状态

LNS统计

Improv/Calls：改进次数/调用次数
Closed：封闭率（找到改进的比例）
Difficulty：平均破坏难度

7. 求解结果

status: OPTIMAL：找到最优解
objective: 94974：最优目标函数值
best_bound: 94974：最优边界（证明是最优）
walltime: 2251.24：实际运行时间
deterministic_time: 4808.1：确定性时间
gap_integral: 12114.5：间隙积分（衡量求解质量）

8. 关键缩写含义

SAT：布尔可满足性问题
CP：约束规划
LP：线性规划
LNS：大邻域搜索
RINS：基于LP舍入的邻域搜索
RENS：基于LP的受限邻域搜索
MIR：混合整数取整割平面
CG：Chvátal-Gomory割平面

提供启发式初始解（MIPStart）

1. 在 CP-SAT 中设置初始解：

CP-SAT 通过 AddHint() 方法接受初始解（提示）。

python 复制代码

from ortools.sat.python import cp_model

model = cp_model.CpModel()
# 定义变量
x = model.NewIntVar(0, 10, 'x')
y = model.NewIntVar(0, 10, 'y')

# !!! 关键：为变量添加初始解提示 (hint)
model.AddHint(x, 7)
model.AddHint(y, 3)

# ... 添加约束和目标 ...
solver = cp_model.CpSolver()
status = solver.Solve(model)

原理：求解器会优先从这些提示值附近开始搜索，但不保证完全遵守。
注意：提供的初始解必须是可行解（满足所有约束），否则提示会被忽略。

2. 在 pywraplp (CBC/SCIP) 中设置初始解：

这通常通过为变量设置 SetInitialSolution() 或通过求解器特定接口实现。

python 复制代码

from ortools.linear_solver import pywraplp

solver = pywraplp.Solver.CreateSolver('CBC')
x = solver.NumVar(0, 10, 'x')
y = solver.IntVar(0, 10, 'y')
# ... 添加约束和目标 ...

# !!! 关键：设置初始解（具体方法可能因后端求解器略有不同）
# 对于CBC，可以通过设置变量值并标记为初始解
solver.SetInitialSolution([x, y], [7.0, 3.0])  # 假设此方法存在
# 更通用的方式是使用求解器特定的参数字符串（例如SCIP支持读取初始解文件）

重要提示 ：pywraplp 的 API 对初始解的支持不如 CP-SAT 直接。更可靠的做法是：
- 对于SCIP ：可以通过 solver.SetSolverSpecificParametersAsString("read my_init.sol") 指定一个包含初始解的文件。
- 通用建议：查阅你所用后端（CBC, SCIP, Gurobi）的文档，找到其设置初始解的官方方法，这通常是加速 MIP 求解最关键的一步。

📊 求解结果解析

求解状态说明

python 复制代码

from ortools.sat.python import cp_model

status = solver.Solve(model)
if status == cp_model.OPTIMAL:
    print('✅ 找到最优解')
elif status == cp_model.FEASIBLE:
    print('⚠️  找到可行解（非最优）')
elif status == cp_model.INFEASIBLE:
    print('❌ 无可行解')
elif status == cp_model.MODEL_INVALID:
    print('❌ 模型无效')
else:
    print('❓ 求解状态未知')

获取求解统计信息

python 复制代码

# 目标函数值
obj_value = solver.ObjectiveValue()

# 求解时间
wall_time = solver.WallTime()  # 毫秒

# 变量取值
x_value = solver.Value(x)

# 输出统计摘要
print(solver.ResponseStats())

第四部分：实战应用、问题解决与学习资源

🚀 快速开始示例（生成计划排程）

python 复制代码

"""
生产排程优化模型示例
使用Google OR-Tools的CP-SAT求解器
"""

from ortools.sat.python import cp_model
import pandas as pd
import numpy as np
from datetime import datetime
import math
import os

class ProductionSchedulingExample:
    """
    生产排程优化模型示例类

    展示如何使用CP-SAT求解器解决两阶段生产排程问题
    """

    def __init__(self, sample_data_file: str = None):
        """
        初始化示例模型

        Args:
            sample_data_file: 示例数据文件路径(可选)
        """
        print("初始化生产排程示例模型")

        # 如果没有提供数据文件，生成示例数据
        if sample_data_file and os.path.exists(sample_data_file):
            self._load_sample_data(sample_data_file)
        else:
            self._generate_sample_data()

        # 初始化参数
        self._init_parameters()

        # 设置求解器
        self._setup_solver()

        # 初始化求解时间
        self.solve_time = 0

    def _generate_sample_data(self):
        """生成示例数据用于演示"""
        print("生成示例数据...")

        # 示例产品数据
        self.products = pd.DataFrame({
            'product_id': [101, 102, 103, 104],
            'product_name': ['Product_A', 'Product_B', 'Product_C', 'Product_D']
        })

        # 示例订单数据
        self.orders = pd.DataFrame({
            'order_id': [1001, 1002, 1003, 1004, 1005],
            'product_id': [101, 102, 103, 104, 101],
            'quantity': [500, 300, 400, 200, 350],
            'due_date_seconds': [86400, 172800, 259200, 345600, 432000],
            'priority': [3, 2, 4, 1, 3]
        })

        # 示例机器数据
        self.machines = pd.DataFrame({
            'machine_id': [1, 2, 3, 4, 5, 6],
            'resource_group': ['Stage_1', 'Stage_1', 'Stage_1', 'Stage_2', 'Stage_2', 'Stage_2'],
            'capacity_type': ['Type_A', 'Type_B', 'Type_A', 'Type_C', 'Type_C', 'Type_D']
        })

        # 示例产能数据
        self.capacity_data = []
        for product in self.products['product_id']:
            for machine in self.machines['machine_id']:
                # 随机生成产能数据
                if machine <= 3:  # Stage 1 machines
                    capacity = np.random.uniform(20, 50)
                else:  # Stage 2 machines
                    capacity = np.random.uniform(15, 40)

                self.capacity_data.append({
                    'product_id': product,
                    'machine_id': machine,
                    'process_name': 'Stage_1' if machine <= 3 else 'Stage_2',
                    'hourly_capacity': round(capacity, 1),
                    'yield_rate': round(np.random.uniform(0.85, 0.98), 2)
                })

        self.capacity_df = pd.DataFrame(self.capacity_data)

        # 示例库存数据
        self.inventory = pd.DataFrame({
            'product_id': [101, 102, 103, 104],
            'stage_1_inventory': [100, 80, 120, 60],
            'stage_2_inventory': [50, 40, 60, 30]
        })

        print("示例数据生成完成")
        print(f"产品数量: {len(self.products)}")
        print(f"订单数量: {len(self.orders)}")
        print(f"机器数量: {len(self.machines)}")

    def _load_sample_data(self, file_path: str):
        """加载示例数据文件"""
        print(f"从文件加载示例数据: {file_path}")

        # 这里可以加载预定义的示例数据文件
        # 实际实现会根据文件格式读取数据
        pass

    def _init_parameters(self):
        """初始化模型参数"""
        print("初始化模型参数...")

        # 时间参数
        self.shift_hours = 8
        self.planning_horizon_days = 10
        self.total_shifts = self.planning_horizon_days * 3  # 每天3个班次

        # 换型参数
        self.stage_1_changeover_hours = 2
        self.stage_2_changeover_hours = 4
        self.inter_stage_delay_hours = 8

        # 资源限制
        self.max_stage_1_machines = 3
        self.max_stage_2_machines = 3
        self.max_changeovers_per_day = 2

        # 生产约束
        self.max_continuous_production_shifts = 6

        print(f"规划周期: {self.planning_horizon_days} 天")
        print(f"总班次: {self.total_shifts}")
        print(f"Stage 1 换型时间: {self.stage_1_changeover_hours} 小时")
        print(f"Stage 2 换型时间: {self.stage_2_changeover_hours} 小时")

    def _setup_solver(self):
        """设置CP-SAT求解器"""
        print("设置CP-SAT求解器...")

        self.model = cp_model.CpModel()
        self.solver = cp_model.CpSolver()

        # 设置求解参数
        self.solver.parameters.max_time_in_seconds = 1800  # 30分钟
        self.solver.parameters.num_search_workers = 4
        self.solver.parameters.log_search_progress = True

        print("求解器设置完成")

    def _calculate_product_demand(self):
        """计算产品需求"""
        demand_by_product = {}

        for _, order in self.orders.iterrows():
            product_id = order['product_id']
            quantity = order['quantity']

            if product_id not in demand_by_product:
                demand_by_product[product_id] = 0
            demand_by_product[product_id] += quantity

        return demand_by_product

    def build_model(self):
        """构建优化模型"""
        print("\n构建优化模型...")

        # 获取产品需求
        product_demand = self._calculate_product_demand()

        # 创建索引映射
        product_ids = list(product_demand.keys())
        product_index_map = {pid: idx for idx, pid in enumerate(product_ids)}

        # 阶段1机器
        stage_1_machines = self.machines[
            self.machines['resource_group'] == 'Stage_1'
        ]['machine_id'].tolist()

        # 阶段2机器
        stage_2_machines = self.machines[
            self.machines['resource_group'] == 'Stage_2'
        ]['machine_id'].tolist()

        # 定义集合
        I = range(len(product_ids))  # 产品索引
        M1 = range(len(stage_1_machines))  # Stage 1 机器索引
        M2 = range(len(stage_2_machines))  # Stage 2 机器索引
        T = range(self.total_shifts)  # 时间班次

        print(f"产品集合大小: {len(I)}")
        print(f"Stage 1 机器集合大小: {len(M1)}")
        print(f"Stage 2 机器集合大小: {len(M2)}")
        print(f"时间班次集合大小: {len(T)}")

        # 创建决策变量
        print("创建决策变量...")

        # 生产标识变量
        produce_s1 = {}  # Stage 1 生产标识
        produce_s2 = {}  # Stage 2 生产标识

        # 换型变量
        changeover_s1 = {}  # Stage 1 换型标识
        changeover_s2 = {}  # Stage 2 换型标识

        # 库存变量
        inventory_s1 = {}  # Stage 1 库存
        inventory_s2 = {}  # Stage 2 库存

        # 生产数量变量（简化的产量）
        production_amount_s1 = {}  # Stage 1 生产数量
        production_amount_s2 = {}  # Stage 2 生产数量

        # 创建变量
        for i in I:
            for m in M1:
                for t in T:
                    produce_s1[(i, m, t)] = self.model.NewBoolVar(
                        f"produce_s1_{i}_{m}_{t}"
                    )
                    # 简化的产量：每个班次固定产量100件
                    production_amount_s1[(i, m, t)] = self.model.NewIntVar(
                        0, 100, f"prod_s1_{i}_{m}_{t}"
                    )
                    # 如果生产，产量=100，否则=0
                    self.model.Add(production_amount_s1[(i, m, t)] == 100).OnlyEnforceIf(
                        produce_s1[(i, m, t)]
                    )
                    self.model.Add(production_amount_s1[(i, m, t)] == 0).OnlyEnforceIf(
                        produce_s1[(i, m, t)].Not()
                    )

        for i in I:
            for m in M2:
                for t in T:
                    produce_s2[(i, m, t)] = self.model.NewBoolVar(
                        f"produce_s2_{i}_{m}_{t}"
                    )
                    production_amount_s2[(i, m, t)] = self.model.NewIntVar(
                        0, 100, f"prod_s2_{i}_{m}_{t}"
                    )
                    self.model.Add(production_amount_s2[(i, m, t)] == 100).OnlyEnforceIf(
                        produce_s2[(i, m, t)]
                    )
                    self.model.Add(production_amount_s2[(i, m, t)] == 0).OnlyEnforceIf(
                        produce_s2[(i, m, t)].Not()
                    )

        # 添加约束
        self._add_constraints(
            produce_s1, produce_s2, changeover_s1, changeover_s2,
            inventory_s1, inventory_s2, production_amount_s1, production_amount_s2,
            I, M1, M2, T, product_demand, product_index_map
        )

        # 保存变量引用
        self.vars = {
            'produce_s1': produce_s1,
            'produce_s2': produce_s2,
            'changeover_s1': changeover_s1,
            'changeover_s2': changeover_s2,
            'inventory_s1': inventory_s1,
            'inventory_s2': inventory_s2,
            'production_amount_s1': production_amount_s1,
            'production_amount_s2': production_amount_s2,
            'product_index_map': product_index_map,
            'stage_1_machines': stage_1_machines,
            'stage_2_machines': stage_2_machines,
            'I': I,
            'M1': M1,
            'M2': M2,
            'T': T,
            'product_demand': product_demand
        }

        # 设置目标函数
        self._set_objective()

        print("模型构建完成")
        print(f"总变量数: {len(self.model.proto.variables)}")
        print(f"总约束数: {len(self.model.proto.constraints)}")

    def _add_constraints(self, produce_s1, produce_s2, changeover_s1, changeover_s2,
                        inventory_s1, inventory_s2, production_amount_s1, production_amount_s2,
                        I, M1, M2, T, product_demand, product_index_map):
        """添加约束条件"""
        print("添加约束条件...")

        # 1. 机器单一任务约束
        for m in M1:
            for t in T:
                # 每台机器每个班次最多生产一个产品
                self.model.Add(sum(produce_s1[(i, m, t)] for i in I) <= 1)

        for m in M2:
            for t in T:
                self.model.Add(sum(produce_s2[(i, m, t)] for i in I) <= 1)

        # 2. 库存平衡约束
        for i in I:
            product_id = list(product_demand.keys())[i]

            # 获取初始库存
            initial_s1_inventory = self.inventory[
                self.inventory['product_id'] == product_id
            ]['stage_1_inventory'].iloc[0]

            initial_s2_inventory = self.inventory[
                self.inventory['product_id'] == product_id
            ]['stage_2_inventory'].iloc[0]

            # 创建库存变量
            for t in T:
                # Stage 1 库存变量
                inventory_s1[(i, t)] = self.model.NewIntVar(
                    0, 10000, f"inv_s1_{i}_{t}"
                )
                # Stage 2 库存变量
                inventory_s2[(i, t)] = self.model.NewIntVar(
                    0, 10000, f"inv_s2_{i}_{t}"
                )

            # Stage 1 库存平衡
            for t in T:
                if t == 0:
                    # 初始库存 + 生产 - 消耗（简化为所有生产都消耗）
                    total_production_s1 = sum(production_amount_s1[(i, m, t)] for m in M1)
                    # 简化的消耗：假设Stage 1生产的产品都转移到Stage 2
                    self.model.Add(
                        inventory_s1[(i, t)] == initial_s1_inventory + total_production_s1
                    )
                else:
                    total_production_s1 = sum(production_amount_s1[(i, m, t)] for m in M1)
                    self.model.Add(
                        inventory_s1[(i, t)] == inventory_s1[(i, t-1)] + total_production_s1
                    )

            # Stage 2 库存平衡
            for t in T:
                if t == 0:
                    total_production_s2 = sum(production_amount_s2[(i, m, t)] for m in M2)
                    # 初始库存 + 生产
                    self.model.Add(
                        inventory_s2[(i, t)] == initial_s2_inventory + total_production_s2
                    )
                else:
                    total_production_s2 = sum(production_amount_s2[(i, m, t)] for m in M2)
                    self.model.Add(
                        inventory_s2[(i, t)] == inventory_s2[(i, t-1)] + total_production_s2
                    )

            # 3. 工序间约束：Stage 2的消耗不能超过Stage 1的库存
            for t in T:
                if t > 0:
                    total_production_s2_t = sum(production_amount_s2[(i, m, t)] for m in M2)
                    # Stage 2的生产不能超过Stage 1在前一个班次的库存
                    self.model.Add(total_production_s2_t <= inventory_s1[(i, t-1)])

        print("约束添加完成")

    def _set_objective(self):
        """设置目标函数"""
        print("设置目标函数...")

        # 获取变量和参数
        inventory_s2 = self.vars['inventory_s2']
        I = self.vars['I']
        T = self.vars['T']
        product_demand = self.vars['product_demand']

        # 创建延迟惩罚变量
        tardiness_penalty = 0

        for i in I:
            product_id = list(product_demand.keys())[i]
            demand = product_demand[product_id]

            # 最后班次的Stage 2库存
            final_inventory = inventory_s2[(i, T[-1])]

            # 延迟量 = 需求 - 最终库存（如果库存不足）
            shortage = self.model.NewIntVar(0, demand, f"shortage_{i}")

            # 正确的方式：约束 shortage >= demand - final_inventory
            # 这样在最小化目标时，如果 demand - final_inventory > 0，
            # shortage 会取这个值；否则 shortage 会取0
            self.model.Add(shortage >= demand - final_inventory)

            # 添加到目标函数
            tardiness_penalty += shortage * 10  # 每个单位延迟的惩罚

        # 最小化总延迟惩罚
        self.model.Minimize(tardiness_penalty)

        print("目标函数设置完成: 最小化延迟惩罚")

    def solve(self):
        """求解模型"""
        print("\n开始求解...")
        start_time = datetime.now()

        status = self.solver.Solve(self.model)

        end_time = datetime.now()
        self.solve_time = (end_time - start_time).total_seconds()

        print(f"求解完成，耗时: {self.solve_time:.2f} 秒")

        if status == cp_model.OPTIMAL:
            print("✓ 找到最优解!")
            print(f"目标函数值: {self.solver.ObjectiveValue()}")
            return True
        elif status == cp_model.FEASIBLE:
            print("✓ 找到可行解")
            print(f"目标函数值: {self.solver.ObjectiveValue()}")
            return True
        else:
            status_names = {
                cp_model.OPTIMAL: "OPTIMAL",
                cp_model.FEASIBLE: "FEASIBLE",
                cp_model.INFEASIBLE: "INFEASIBLE",
                cp_model.MODEL_INVALID: "MODEL_INVALID",
                cp_model.UNKNOWN: "UNKNOWN"
            }
            status_name = status_names.get(status, f"未知状态({status})")
            print(f"✗ 求解失败，状态: {status_name}")
            return False

    def extract_results(self):
        """提取结果"""
        if not hasattr(self, 'solver'):
            print("请先求解模型")
            return None

        if not hasattr(self, 'solve_time'):
            print("未找到求解时间信息")
            self.solve_time = 0

        print("\n提取求解结果...")

        # 获取变量
        produce_s1 = self.vars['produce_s1']
        produce_s2 = self.vars['produce_s2']
        production_amount_s1 = self.vars['production_amount_s1']
        production_amount_s2 = self.vars['production_amount_s2']
        product_index_map = self.vars['product_index_map']
        stage_1_machines = self.vars['stage_1_machines']
        stage_2_machines = self.vars['stage_2_machines']

        # 反向产品索引映射
        index_product_map = {v: k for k, v in product_index_map.items()}

        # 生成Stage 1生产计划
        s1_schedule = []
        for (i, m_idx, t), var in produce_s1.items():
            if self.solver.Value(var) > 0.5:  # 布尔变量值为1
                product_id = index_product_map[i]
                machine_id = stage_1_machines[m_idx]
                quantity = self.solver.Value(production_amount_s1[(i, m_idx, t)])

                s1_schedule.append({
                    'product_id': product_id,
                    'machine_id': machine_id,
                    'shift': t + 1,
                    'quantity': quantity
                })

        # 生成Stage 2生产计划
        s2_schedule = []
        for (i, m_idx, t), var in produce_s2.items():
            if self.solver.Value(var) > 0.5:
                product_id = index_product_map[i]
                machine_id = stage_2_machines[m_idx]
                quantity = self.solver.Value(production_amount_s2[(i, m_idx, t)])

                s2_schedule.append({
                    'product_id': product_id,
                    'machine_id': machine_id,
                    'shift': t + 1,
                    'quantity': quantity
                })

        # 创建DataFrame
        s1_df = pd.DataFrame(s1_schedule)
        s2_df = pd.DataFrame(s2_schedule)

        print(f"Stage 1 生产计划记录数: {len(s1_df)}")
        print(f"Stage 2 生产计划记录数: {len(s2_df)}")

        return {
            'stage_1_schedule': s1_df,
            'stage_2_schedule': s2_df,
            'objective_value': self.solver.ObjectiveValue(),
            'solve_time_seconds': self.solve_time
        }

    def print_summary(self):
        """打印结果摘要"""
        results = self.extract_results()

        if results:
            print("\n" + "="*50)
            print("生产排程结果摘要")
            print("="*50)

            print(f"目标函数值: {results['objective_value']}")
            print(f"求解时间: {results['solve_time_seconds']:.2f} 秒")

            s1_df = results['stage_1_schedule']
            s2_df = results['stage_2_schedule']

            if not s1_df.empty:
                print(f"\nStage 1 生产安排:")
                print(f"  总生产批次数: {len(s1_df)}")
                print(f"  涉及产品数: {s1_df['product_id'].nunique()}")
                print(f"  使用机器数: {s1_df['machine_id'].nunique()}")
                print(f"  总产量: {s1_df['quantity'].sum()} 件")

            if not s2_df.empty:
                print(f"\nStage 2 生产安排:")
                print(f"  总生产批次数: {len(s2_df)}")
                print(f"  涉及产品数: {s2_df['product_id'].nunique()}")
                print(f"  使用机器数: {s2_df['machine_id'].nunique()}")
                print(f"  总产量: {s2_df['quantity'].sum()} 件")

            print("="*50)


def run_example():
    """运行示例"""
    print("="*60)
    print("生产排程优化示例")
    print("="*60)

    try:
        # 创建模型实例
        model = ProductionSchedulingExample()

        # 构建模型
        model.build_model()

        # 求解模型
        if model.solve():
            # 打印结果摘要
            model.print_summary()

            # 提取详细结果
            results = model.extract_results()

            # 可以在这里保存结果到文件
            if results:
                output_dir = './example_output'
                os.makedirs(output_dir, exist_ok=True)

                # 保存计划到CSV
                results['stage_1_schedule'].to_csv(
                    f'{output_dir}/stage_1_schedule.csv', index=False
                )
                results['stage_2_schedule'].to_csv(
                    f'{output_dir}/stage_2_schedule.csv', index=False
                )

                print(f"\n结果已保存到: {output_dir}")
        else:
            print("\n求解失败，请检查模型设置")

    except Exception as e:
        print(f"\n执行过程中发生错误: {str(e)}")
        import traceback
        traceback.print_exc()

    print("\n" + "="*60)
    print("示例程序结束")
    print("="*60)


if __name__ == '__main__':
    run_example()

ortools运行报错：OSError: [WinError 127] 找不到指定的程序。

python 复制代码

from ortools.sat.python import cp_model
from ortools.linear_solver import pywraplp

在运行ortools导入语句的Python程序时出现错误：

复制代码

Traceback (most recent call last):
  File "D:\AiProject\zj\3_production_scheduling_pywraplp.py", line 7, in <module>
    from ortools.linear_solver import pywraplp
  File "D:\anaconda3\Lib\site-packages\ortools\__init__.py", line 72, in <module>
    _load_ortools_libs()
    ~~~~~~~~~~~~~~~~~~^^
  File "D:\anaconda3\Lib\site-packages\ortools\__init__.py", line 67, in _load_ortools_libs
    WinDLL(dll_path)
    ~~~~~~^^^^^^^^^^
  File "D:\anaconda3\Lib\ctypes\__init__.py", line 390, in __init__
    self._handle = _dlopen(self._name, mode)
                   ~~~~~~~^^^^^^^^^^^^^^^^^^
OSError: [WinError 127] 找不到指定的程序。

两个解决方法

1. 安装 Microsoft Visual C++ Redistributable

这个错误通常是由于缺少必要的C++运行库导致的。OR-Tools需要这些库来加载其原生DLL文件。

解决方案：

访问微软官网下载并安装最新版的 Visual C++ Redistributable
建议同时安装x86和x64版本
安装完成后重启计算机

2. 将ortools导入语句放在程序第一行

在某些情况下，Python的导入顺序会影响库的加载。将ortools导入放在程序的最开始可以解决这个问题。

修改前的代码：

python 复制代码

# 其他导入
import numpy as np
import pandas as pd

# OR-Tools导入在中间
from ortools.sat.python import cp_model
from ortools.linear_solver import pywraplp

# 其他代码...

修改后的代码：

python 复制代码

# 将OR-Tools导入放在第一行
from ortools.sat.python import cp_model
from ortools.linear_solver import pywraplp

# 其他导入放在后面
import numpy as np
import pandas as pd

# 其他代码...

📚 学习资源

类别	工具/项目名称	特点与用途	参考信息与链接
数学规划求解器	COPT (杉数)	国产商业求解器，性能优异。	官网：杉数科技COPT。
商业	Gurobi	业界领先的商业求解器，高性能。	官网：Gurobi Optimization。
闭源	MindOpt (阿里)	阿里达摩院推出的优化求解器。	官网：阿里云MindOpt。
启发式算法库	scikit-opt	提供遗传算法、模拟退火等启发式算法，用于快速寻找优质可行解。	scikit-opt中文文档。
建模语言与工具	MiniZinc	一种声明式的高层建模语言，可将模型与多种后端求解器（包括OR-Tools）解耦。适合快速原型验证和算法研究。	MiniZinc官网。
领域专用框架	PyJobShop	一个专门用于作业车间调度问题（JSP）建模、求解和可视化的Python库，基于OR-Tools等求解器构建，提供标准案例和评估工具。	PyJobShop文档。
教程与学习资源	cpsat-primer	一个专注于 Google OR-Tools CP-SAT 求解器的入门教程和代码示例库，包含大量带注释的实战案例，是深入掌握CP-SAT的绝佳补充材料。	GitHub仓库：cpsat-primer。
官方核心资源	Google OR-Tools	本指南核心工具，开源运筹学库。	官方文档：developers.google.com/optimization GitHub ：google/or-tools 社区：Stack Overflow

APS系统与OR-Tools完全指南：智能排产与优化算法实战解析

APS系统与OR-Tools完全指南：智能排产与优化算法实战解析

第一部分：APS系统概述与核心理论

🔍 什么是APS系统？

🔍 APS系统的核心价值与技术特点

📊 核心优化方法对比与MILP的应用

🧩 MILP的核心思想与在APS中的应用

🔄 MILP的局限与其他高级算法

🔍 为何APS没有"通用解"：必须紧贴业务建模的核心原因

🛠️ 如何选择与实施APS

第二部分：APS中的甘特图与优化建模实践

APS中的甘特图

🧠 甘特图在APS中的核心作用

📊 APS中甘特图的多样形式

🛠️ 优化建模技巧

1. 减少不必要的变量

2. 最小化变量的上下限

3. 一个约束一个约束的增加（迭代建模）

4. 大型排程的小范围测试策略

5. 结果验证与增量开发

6. 性能优化技巧

7. 调试与日志记录

第三部分：Google OR-Tools 完全指南：从求解器选型到实战应用

🧭 概述

📌 快速选择指南

🧩 核心求解器一览

🚀 快速开始

1. 安装

2. 通用建模流程（四步法）

📦 核心模块详解

pywraplp：线性规划/混合整数规划模块

支持的求解器后端

常用方法示例

pywraplp 求解器参数设置

CP-SAT：约束规划模块

核心建模方法

CP-SAT 求解器参数

CP-SAT日志输出说明

1. 求解启动部分

2. 模型统计

3. 预处理（Presolve）阶段

4. 搜索过程关键术语

5. 边界改进

6. 统计信息部分

7. 求解结果

8. 关键缩写含义

提供启发式初始解（MIPStart）

📊 求解结果解析

求解状态说明

获取求解统计信息

第四部分：实战应用、问题解决与学习资源

🚀 快速开始示例（生成计划排程）

ortools运行报错：OSError: [WinError 127] 找不到指定的程序。

两个解决方法

1. 安装 Microsoft Visual C++ Redistributable

2. 将ortools导入语句放在程序第一行

📚 学习资源

`pywraplp` 求解器参数设置