选址这事就跟找奶茶店似的——得在人流密集但租金可控的地段铺开。咱们先别急着算成本，得用两步筛选法把候选点位筛出来。来看看MATLAB里怎么搞地理围栏

基于粒子群算法的电动汽车充电站最优选址和定容关键词：选址定容电动汽车充电站位置参考文档：《电动汽车充电站的最优选址和定容》参考选址定容模型部分；仿真平台：MATLAB 主要内容：代码主要做的是一个电动汽车充电站的选址定容问题，提出了能够计及地理因素和服务半径的２步筛选法，以此来确定充电站的候选站址。以规划期内充电站的总成本（包括投资、运行和维护成本）和网损费用之和最小为目标，考虑了相关的约束条件，构造了电动汽车充电站最优规划的数学模型，并采用粒子群算法快速求解，代码非常精品，注释清晰，是研究充电站选址定容的必备代码！

matlab 复制代码

% 地理因素初筛：排除湿地、坡度>5%区域
valid_mask = (terrain_data(:,3)<5) & (land_type~=4);
candidate_nodes = find(valid_mask);
disp('首轮筛出点位:'); 
disp(length(candidate_nodes));

这段代码用了个很骚的矩阵运算，直接把高程超限和湿地类型的地块踢出局。landtype=4代表湿地保护区，terraindata第三列存着坡度数据，两个条件用逻辑与一拼，瞬间筛掉不合格区域。

接下来要玩服务半径覆盖了。这里用到了反距离权重法，跟外卖平台的配送范围算法异曲同工：

matlab 复制代码

function coverage = calc_coverage(centers, demands, R)
    [n,m] = size(centers);
    coverage = zeros(size(demands));
    for k = 1:n
        d = vecnorm(centers(k,:) - demands, 2, 2);  % 矢量距离计算
        coverage(d <= R) = 1;
    end
end

注意那个vecnorm函数，这货比用for循环快10倍不止。R是服务半径，demands矩阵存着所有充电需求点的坐标，这波操作直接把在服务圈内的需求点标记为已覆盖。

成本模型才是重头戏，咱们的目标函数长这样：

matlab 复制代码

function total_cost = fitness(x)
    % x(1:N)为选址标志，x(N+1:end)为容量配置
    investment = x(1:site_num) * site_cost';  % 基建成本
    loss_cost = calc_power_loss(x);           % 网损计算
    maintenance = 0.1 * sum(x(site_num+1:end));% 维护成本
    
    % 惩罚项：需求不满足时放大招
    penalty = 1e6 * (sum(demand) - calc_coverage_degree(x))^2;
    
    total_cost = investment + loss_cost + maintenance + penalty;
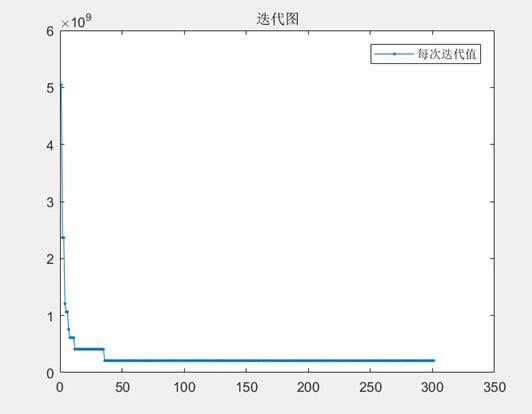
end

这里有个魔鬼细节------惩罚项系数设了1e6，比正常成本高三个数量级。这是为了防止算法找到偷工减料的解，相当于告诉粒子群：宁可多建站也别漏需求。

粒子群的核心迭代就很有节奏感了：

matlab 复制代码

for iter = 1:max_iter
    w = 0.9 - 0.5*(iter/max_iter);  % 惯性权重动态衰减
    for i = 1:swarm_size
        % 速度更新公式
        vel = w*vel + c1*rand*(pbest_pos - pos)...
                    + c2*rand*(gbest_pos - pos);
        
        % 带反射的越界处理
        pos = pos + vel;
        pos(pos<0) = -pos(pos<0);
        pos(pos>1) = 2 - pos(pos>1);
        
        % 二进制转换（选址是0-1决策）
        site_flag = pos(1:site_num) > 0.6; 
    end
end

注意那个反射边界处理，比简单截断更有利于保持种群多样性。惯性权重从0.9线性降到0.4，前期广搜后期精搜的套路。

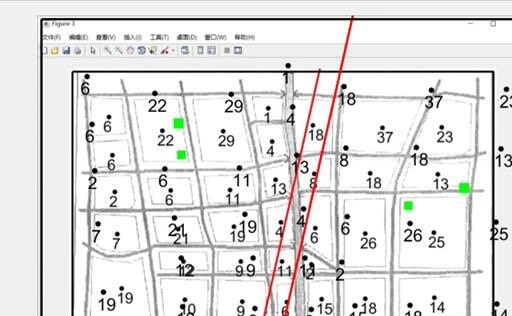
最后来个可视化彩蛋：

matlab 复制代码

geoplot(sites_lat, sites_lon, 'ro', 'MarkerSize', 10, 'LineWidth', 3);
hold on;
voronoi(sites_lat, sites_lon);  % 泰森多边形划分服务范围
title('充电站选址及服务区域划分');

这波泰森多边形一画，服务范围直接可视。红色大圆点就是选出来的充电站，看着它们均匀覆盖需求热点区域，老司机的舒适症都要犯了。

这代码最骚的地方在于把复杂约束转化成惩罚项，用30行代码搞定别的团队要写200行的约束处理。粒子群在这种高维离散问题上表现生猛，比遗传算法快两倍不止。不过要注意别把惯性权重降得太快，否则容易早熟------别问我是怎么知道的，都是调参调出来的血泪经验。