注:本文是之前记录的草稿,估计短期内没有时间写文章。先发出来,以后时机合适再整理重新发布。
量子密钥分发-BB84协议
- [1. 前言](#1. 前言)
- [2. BB84协议表示0和1的方案](#2. BB84协议表示0和1的方案)
- [3. BB84 协议量子线路模型](#3. BB84 协议量子线路模型)
- [4. 状态演化分析](#4. 状态演化分析)
- [5. 安全性分析](#5. 安全性分析)
- 参考文献
1. 前言
BB84协议是Charles Bennett 和 Gilles Brassard 于 1984 年提出的第一个(离散变量)量子密钥分发协议 。本文介绍了BB84 协议的原理架构、量子态演变和安全性分析。
2. BB84协议表示0和1的方案
(1)以50%的概率随机地用状态 ∣ 0 ⟩ |0\rangle ∣0⟩ 和 ∣ 0 ⟩ + ∣ 1 ⟩ 2 \frac{|0\rangle+|1\rangle}{\sqrt{2}} 2 ∣0⟩+∣1⟩ 表示0。
(2)以50%的概率随机地用状态 ∣ 1 ⟩ |1\rangle ∣1⟩ 和 ∣ 0 ⟩ − ∣ 1 ⟩ 2 \frac{|0\rangle-|1\rangle}{\sqrt{2}} 2 ∣0⟩−∣1⟩ 表示1。
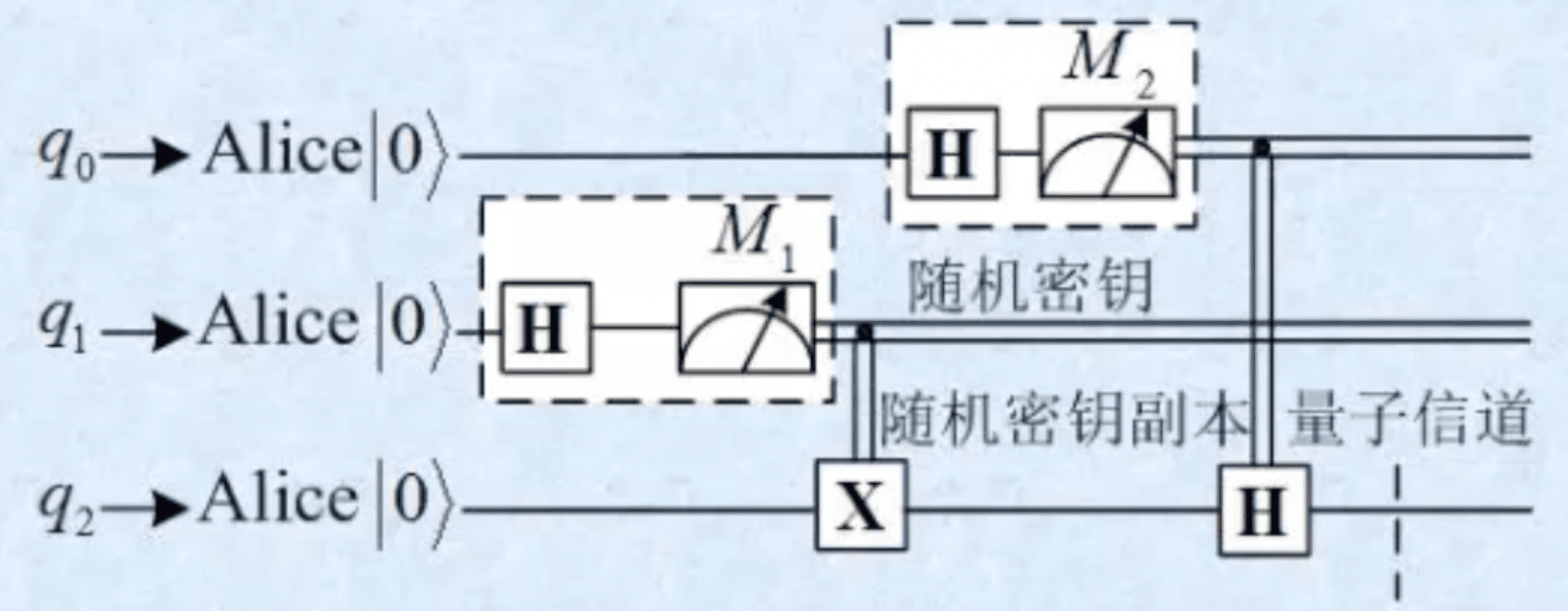
注意此处的是经典结果控制 X 和 H 门,不是受控 X 门和受控 H 门。
3. BB84 协议量子线路模型
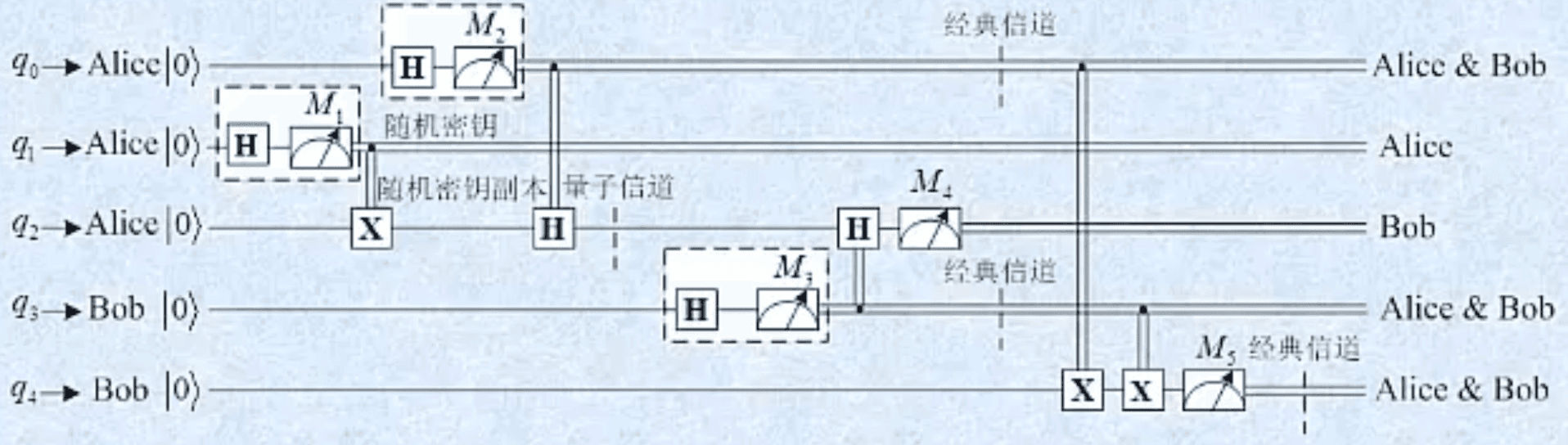
q 4 q4 q4作为指示用, M 2 = M 3 M_2=M_3 M2=M3时,即 00 或 11 时, M 1 M_1 M1和 M 4 M_4 M4结果才一致,这时候 M 5 = 0 M_5=0 M5=0;否则 M 5 = 1 M_5=1 M5=1。
4. 状态演化分析
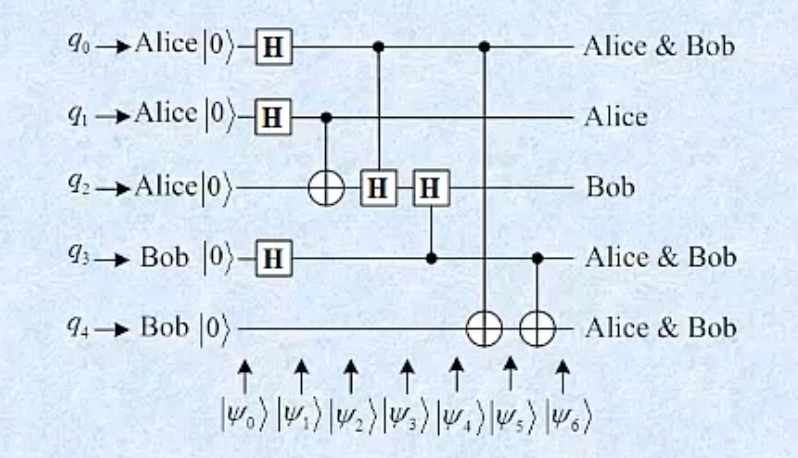
q 4 ≺ q 3 ≺ q 2 ≺ q 1 ≺ q 0 q_4 \prec q_3 \prec q_2 \prec q_1 \prec q_0 q4≺q3≺q2≺q1≺q0
∣ ψ 0 ⟩ = ∣ 00000 ⟩ |\psi_0\rangle = |00000\rangle ∣ψ0⟩=∣00000⟩
∣ ψ 1 ⟩ = ∣ 0 ⟩ ∣ 0 ⟩ + ∣ 1 ⟩ 2 ∣ 0 ⟩ ∣ 0 ⟩ + ∣ 1 ⟩ 2 ∣ 0 ⟩ + ∣ 1 ⟩ 2 = ∣ 0 ⟩ ∣ 0 ⟩ + ∣ 1 ⟩ 2 ∣ 00 ⟩ + ∣ 01 ⟩ 2 ∣ 0 ⟩ + ∣ 1 ⟩ 2 \begin{aligned} |\psi_1\rangle &= |0\rangle \frac{|0\rangle + |1\rangle}{\sqrt{2}} |0\rangle \frac{|0\rangle + |1\rangle}{\sqrt{2}} \frac{|0\rangle + |1\rangle}{\sqrt{2}} \\ &= |0\rangle \frac{|0\rangle + |1\rangle}{\sqrt{2}} \frac{|00\rangle + |01\rangle}{\sqrt{2}} \frac{|0\rangle + |1\rangle}{\sqrt{2}} \end{aligned} ∣ψ1⟩=∣0⟩2 ∣0⟩+∣1⟩∣0⟩2 ∣0⟩+∣1⟩2 ∣0⟩+∣1⟩=∣0⟩2 ∣0⟩+∣1⟩2 ∣00⟩+∣01⟩2 ∣0⟩+∣1⟩
∣ ψ 2 ⟩ = ∣ 0 ⟩ ∣ 0 ⟩ + ∣ 1 ⟩ 2 ∣ 00 ⟩ + ∣ 11 ⟩ 2 ∣ 0 ⟩ + ∣ 1 ⟩ 2 = ∣ 0 ⟩ ( ∣ 0 ⟩ + ∣ 1 ⟩ 2 ∣ 00 ⟩ + ∣ 11 ⟩ 2 ∣ 0 ⟩ + ∣ 0 ⟩ + ∣ 1 ⟩ 2 ∣ 00 ⟩ + ∣ 11 ⟩ 2 ∣ 1 ⟩ ) \begin{aligned} |\psi_2\rangle &= |0\rangle \frac{|0\rangle + |1\rangle}{\sqrt{2}} \frac{|00\rangle + |11\rangle}{\sqrt{2}} \frac{|0\rangle + |1\rangle}{\sqrt{2}} \\ &= |0\rangle \left( \frac{|0\rangle + |1\rangle}{\sqrt{2}} \frac{|00\rangle + |11\rangle}{2} |0\rangle + \frac{|0\rangle + |1\rangle}{\sqrt{2}} \frac{|00\rangle + |11\rangle}{2} |1\rangle \right) \end{aligned} ∣ψ2⟩=∣0⟩2 ∣0⟩+∣1⟩2 ∣00⟩+∣11⟩2 ∣0⟩+∣1⟩=∣0⟩(2 ∣0⟩+∣1⟩2∣00⟩+∣11⟩∣0⟩+2 ∣0⟩+∣1⟩2∣00⟩+∣11⟩∣1⟩)
∣ ψ 3 ⟩ = ∣ 0 ⟩ ( ∣ 0 ⟩ + ∣ 1 ⟩ 2 ∣ 00 ⟩ + ∣ 11 ⟩ 2 ∣ 0 ⟩ + ∣ 0 ⟩ + ∣ 1 ⟩ 2 ∣ 0 ⟩ + ∣ 1 ⟩ 2 ∣ 0 ⟩ + ∣ 0 ⟩ − ∣ 1 ⟩ 2 ∣ 1 ⟩ 2 ∣ 1 ⟩ ) = ∣ 0 ⟩ ( ∣ 0 ⟩ + ∣ 1 ⟩ 2 ∣ 00 ⟩ + ∣ 11 ⟩ 2 ∣ 0 ⟩ + ∣ 0 ⟩ + ∣ 1 ⟩ 2 ∣ 00 ⟩ + ∣ 10 ⟩ + ∣ 01 ⟩ − ∣ 11 ⟩ 2 2 ∣ 1 ⟩ ) = ∣ 0 ⟩ [ ∣ 0 ⟩ ( ∣ 00 ⟩ + ∣ 11 ⟩ ) + ∣ 1 ⟩ ( ∣ 00 ⟩ + ∣ 11 ⟩ ) 2 2 ∣ 0 ⟩ + ∣ 0 ⟩ ( ∣ 00 ⟩ + ∣ 10 ⟩ + ∣ 01 ⟩ − ∣ 11 ⟩ ) 4 ∣ 1 ⟩ + ∣ 1 ⟩ ( ∣ 00 ⟩ + ∣ 10 ⟩ + ∣ 01 ⟩ − ∣ 11 ⟩ ) 4 ∣ 1 ⟩ ] \begin{aligned} |\psi_3\rangle &= |0\rangle \left( \frac{|0\rangle + |1\rangle}{\sqrt{2}} \frac{|00\rangle + |11\rangle}{2} |0\rangle + \frac{|0\rangle + |1\rangle}{\sqrt{2}} \frac{\frac{|0\rangle + |1\rangle}{\sqrt{2}}|0\rangle + \frac{|0\rangle - |1\rangle}{\sqrt{2}}|1\rangle}{2} |1\rangle \right) \\ &= |0\rangle \left( \frac{|0\rangle + |1\rangle}{\sqrt{2}} \frac{|00\rangle + |11\rangle}{2} |0\rangle + \frac{|0\rangle + |1\rangle}{\sqrt{2}} \frac{|00\rangle + |10\rangle + |01\rangle - |11\rangle}{2\sqrt{2}} |1\rangle \right) \\ &= |0\rangle \left[ \frac{|0\rangle(|00\rangle + |11\rangle) + |1\rangle(|00\rangle + |11\rangle)}{2\sqrt{2}} |0\rangle \right. \\ &\quad + \frac{|0\rangle(|00\rangle + |10\rangle + |01\rangle - |11\rangle)}{4} |1\rangle \\ &\quad \left. + \frac{|1\rangle(|00\rangle + |10\rangle + |01\rangle - |11\rangle)}{4} |1\rangle \right] \end{aligned} ∣ψ3⟩=∣0⟩ 2 ∣0⟩+∣1⟩2∣00⟩+∣11⟩∣0⟩+2 ∣0⟩+∣1⟩22 ∣0⟩+∣1⟩∣0⟩+2 ∣0⟩−∣1⟩∣1⟩∣1⟩ =∣0⟩(2 ∣0⟩+∣1⟩2∣00⟩+∣11⟩∣0⟩+2 ∣0⟩+∣1⟩22 ∣00⟩+∣10⟩+∣01⟩−∣11⟩∣1⟩)=∣0⟩[22 ∣0⟩(∣00⟩+∣11⟩)+∣1⟩(∣00⟩+∣11⟩)∣0⟩+4∣0⟩(∣00⟩+∣10⟩+∣01⟩−∣11⟩)∣1⟩+4∣1⟩(∣00⟩+∣10⟩+∣01⟩−∣11⟩)∣1⟩]
∣ ψ 4 ⟩ = ∣ 0 ⟩ [ ∣ 0 ⟩ ( ∣ 00 ⟩ + ∣ 11 ⟩ ) + ∣ 1 ⟩ ( ∣ 0 ⟩ + ∣ 1 ⟩ 2 ∣ 0 ⟩ + ∣ 0 ⟩ − ∣ 1 ⟩ 2 ∣ 1 ⟩ ) 2 2 ∣ 0 ⟩ + ∣ 0 ⟩ ( ∣ 00 ⟩ + ∣ 10 ⟩ + ∣ 01 ⟩ − ∣ 11 ⟩ ) 4 ∣ 1 ⟩ + ∣ 1 ⟩ ( ∣ 0 ⟩ + ∣ 1 ⟩ 2 ∣ 0 ⟩ + ∣ 0 ⟩ − ∣ 1 ⟩ 2 ∣ 0 ⟩ + ∣ 0 ⟩ + ∣ 1 ⟩ 2 ∣ 1 ⟩ − ∣ 0 ⟩ − ∣ 1 ⟩ 2 ∣ 1 ⟩ ) 4 ∣ 1 ⟩ ] = ∣ 0 ⟩ ∣ 0 ⟩ ( ∣ 00 ⟩ + ∣ 11 ⟩ ) 2 2 ∣ 0 ⟩ + ∣ 0 ⟩ ∣ 1 ⟩ ( ∣ 00 ⟩ + ∣ 10 ⟩ + ∣ 01 ⟩ − ∣ 11 ⟩ ) 4 ∣ 0 ⟩ + ∣ 0 ⟩ ∣ 0 ⟩ ( ∣ 00 ⟩ + ∣ 10 ⟩ + ∣ 01 ⟩ − ∣ 11 ⟩ ) 4 ∣ 1 ⟩ + ∣ 0 ⟩ ∣ 1 ⟩ ( ∣ 00 ⟩ + ∣ 11 ⟩ ) 2 2 ∣ 1 ⟩ \begin{aligned} |\psi_4\rangle &= |0\rangle \left[ \frac{|0\rangle(|00\rangle + |11\rangle) + |1\rangle \left( \frac{|0\rangle+|1\rangle}{\sqrt{2}}|0\rangle + \frac{|0\rangle-|1\rangle}{\sqrt{2}}|1\rangle \right)}{2\sqrt{2}} |0\rangle \right. \\ &\quad + \frac{|0\rangle(|00\rangle + |10\rangle + |01\rangle - |11\rangle)}{4} |1\rangle \\ &\quad \left. + \frac{|1\rangle \left( \frac{|0\rangle+|1\rangle}{\sqrt{2}}|0\rangle + \frac{|0\rangle-|1\rangle}{\sqrt{2}}|0\rangle + \frac{|0\rangle+|1\rangle}{\sqrt{2}}|1\rangle - \frac{|0\rangle-|1\rangle}{\sqrt{2}}|1\rangle \right)}{4} |1\rangle \right] \\ &= \frac{|0\rangle|0\rangle(|00\rangle + |11\rangle)}{2\sqrt{2}} |0\rangle + \frac{|0\rangle|1\rangle(|00\rangle + |10\rangle + |01\rangle - |11\rangle)}{4} |0\rangle \\ &\quad + \frac{|0\rangle|0\rangle(|00\rangle + |10\rangle + |01\rangle - |11\rangle)}{4} |1\rangle + \frac{|0\rangle|1\rangle(|00\rangle + |11\rangle)}{2\sqrt{2}} |1\rangle \end{aligned} ∣ψ4⟩=∣0⟩ 22 ∣0⟩(∣00⟩+∣11⟩)+∣1⟩(2 ∣0⟩+∣1⟩∣0⟩+2 ∣0⟩−∣1⟩∣1⟩)∣0⟩+4∣0⟩(∣00⟩+∣10⟩+∣01⟩−∣11⟩)∣1⟩+4∣1⟩(2 ∣0⟩+∣1⟩∣0⟩+2 ∣0⟩−∣1⟩∣0⟩+2 ∣0⟩+∣1⟩∣1⟩−2 ∣0⟩−∣1⟩∣1⟩)∣1⟩ =22 ∣0⟩∣0⟩(∣00⟩+∣11⟩)∣0⟩+4∣0⟩∣1⟩(∣00⟩+∣10⟩+∣01⟩−∣11⟩)∣0⟩+4∣0⟩∣0⟩(∣00⟩+∣10⟩+∣01⟩−∣11⟩)∣1⟩+22 ∣0⟩∣1⟩(∣00⟩+∣11⟩)∣1⟩
∣ ψ 5 ⟩ = ∣ 0 ⟩ ∣ 0 ⟩ ( ∣ 00 ⟩ + ∣ 11 ⟩ ) 2 2 ∣ 0 ⟩ + ∣ 0 ⟩ ∣ 1 ⟩ ( ∣ 00 ⟩ + ∣ 10 ⟩ + ∣ 01 ⟩ − ∣ 11 ⟩ ) 4 ∣ 0 ⟩ + ∣ 1 ⟩ ∣ 0 ⟩ ( ∣ 00 ⟩ + ∣ 10 ⟩ + ∣ 01 ⟩ − ∣ 11 ⟩ ) 4 ∣ 1 ⟩ + ∣ 1 ⟩ ∣ 1 ⟩ ( ∣ 00 ⟩ + ∣ 11 ⟩ ) 2 2 ∣ 1 ⟩ \begin{aligned} |\psi_5\rangle = & \frac{|0\rangle|0\rangle(|00\rangle + |11\rangle)}{2\sqrt{2}}|0\rangle + \frac{|0\rangle|1\rangle(|00\rangle + |10\rangle + |01\rangle - |11\rangle)}{4}|0\rangle \\ & + \frac{|1\rangle|0\rangle(|00\rangle + |10\rangle + |01\rangle - |11\rangle)}{4}|1\rangle + \frac{|1\rangle|1\rangle(|00\rangle + |11\rangle)}{2\sqrt{2}}|1\rangle \end{aligned} ∣ψ5⟩=22 ∣0⟩∣0⟩(∣00⟩+∣11⟩)∣0⟩+4∣0⟩∣1⟩(∣00⟩+∣10⟩+∣01⟩−∣11⟩)∣0⟩+4∣1⟩∣0⟩(∣00⟩+∣10⟩+∣01⟩−∣11⟩)∣1⟩+22 ∣1⟩∣1⟩(∣00⟩+∣11⟩)∣1⟩
∣ ψ 6 ⟩ = ∣ 0 ⟩ ∣ 0 ⟩ ( ∣ 00 ⟩ + ∣ 11 ⟩ ) 2 2 ∣ 0 ⟩ + ∣ 1 ⟩ ∣ 1 ⟩ ( ∣ 00 ⟩ + ∣ 10 ⟩ + ∣ 01 ⟩ − ∣ 11 ⟩ ) 4 ∣ 0 ⟩ + ∣ 1 ⟩ ∣ 0 ⟩ ( ∣ 00 ⟩ + ∣ 10 ⟩ + ∣ 01 ⟩ − ∣ 11 ⟩ ) 4 ∣ 1 ⟩ + ∣ 0 ⟩ ∣ 1 ⟩ ( ∣ 00 ⟩ + ∣ 11 ⟩ ) 2 2 ∣ 1 ⟩ = 1 2 2 ∣ 0 ⟩ [ ∣ 0 ⟩ ( ∣ 00 ⟩ + ∣ 11 ⟩ ) ∣ 0 ⟩ + ∣ 1 ⟩ ( ∣ 00 ⟩ + ∣ 11 ⟩ ) ∣ 1 ⟩ ] + 1 4 ∣ 1 ⟩ ( ∣ 0 ⟩ ( ∣ 00 ⟩ + ∣ 01 ⟩ + ∣ 10 ⟩ − ∣ 11 ⟩ ) ∣ 1 ⟩ + ∣ 1 ⟩ ( ∣ 00 ⟩ + ∣ 01 ⟩ + ∣ 10 ⟩ − ∣ 11 ⟩ ) ∣ 0 ⟩ ) \begin{aligned} |\psi_6\rangle = & \frac{|0\rangle|0\rangle(|00\rangle + |11\rangle)}{2\sqrt{2}}|0\rangle + \frac{|1\rangle|1\rangle(|00\rangle + |10\rangle + |01\rangle - |11\rangle)}{4}|0\rangle \\ & + \frac{|1\rangle|0\rangle(|00\rangle + |10\rangle + |01\rangle - |11\rangle)}{4}|1\rangle + \frac{|0\rangle|1\rangle(|00\rangle + |11\rangle)}{2\sqrt{2}}|1\rangle \\ = & \frac{1}{2\sqrt{2}}|0\rangle \left[ |0\rangle(|00\rangle + |11\rangle)|0\rangle + |1\rangle(|00\rangle + |11\rangle)|1\rangle \right] \\ & + \frac{1}{4}|1\rangle \left( |0\rangle(|00\rangle + |01\rangle + |10\rangle - |11\rangle)|1\rangle + |1\rangle(|00\rangle + |01\rangle + |10\rangle - |11\rangle)|0\rangle \right) \end{aligned} ∣ψ6⟩==22 ∣0⟩∣0⟩(∣00⟩+∣11⟩)∣0⟩+4∣1⟩∣1⟩(∣00⟩+∣10⟩+∣01⟩−∣11⟩)∣0⟩+4∣1⟩∣0⟩(∣00⟩+∣10⟩+∣01⟩−∣11⟩)∣1⟩+22 ∣0⟩∣1⟩(∣00⟩+∣11⟩)∣1⟩22 1∣0⟩[∣0⟩(∣00⟩+∣11⟩)∣0⟩+∣1⟩(∣00⟩+∣11⟩)∣1⟩]+41∣1⟩(∣0⟩(∣00⟩+∣01⟩+∣10⟩−∣11⟩)∣1⟩+∣1⟩(∣00⟩+∣01⟩+∣10⟩−∣11⟩)∣0⟩)
观察 ∣ ψ 6 ⟩ |\psi_6\rangle ∣ψ6⟩的前半部分,当测量指示器 q 4 = 0 q_4=0 q4=0 时, q 0 q_0 q0 和 q 3 q_3 q3 的结果为 00、11, q 1 q_1 q1 和 q 2 q_2 q2 的结果为 00、11。
1 2 2 ∣ 0 ⟩ [ ∣ 0 ⟩ ( ∣ 00 ⟩ + ∣ 11 ⟩ ) ∣ 0 ⟩ + ∣ 1 ⟩ ( ∣ 00 ⟩ + ∣ 11 ⟩ ) ∣ 1 ⟩ ] \frac{1}{2\sqrt{2}}|0\rangle[|0\rangle(|00\rangle+|11\rangle)|0\rangle+|1\rangle(|00\rangle+|11\rangle)|1\rangle] 22 1∣0⟩[∣0⟩(∣00⟩+∣11⟩)∣0⟩+∣1⟩(∣00⟩+∣11⟩)∣1⟩]
观察 ∣ ψ 6 ⟩ |\psi_6\rangle ∣ψ6⟩的后半部分,当测量指示器 q 4 = 1 q_4=1 q4=1 时, q 0 q_0 q0 和 q 3 q_3 q3 的结果为 01、10, q 1 q_1 q1 和 q 2 q_2 q2 的结果为 00、01、10、11。
1 4 ∣ 1 ⟩ ( ∣ 0 ⟩ ( ∣ 00 ⟩ + ∣ 01 ⟩ + ∣ 10 ⟩ − ∣ 11 ⟩ ) ∣ 1 ⟩ + ∣ 1 ⟩ ( ∣ 00 ⟩ + ∣ 01 ⟩ + ∣ 10 ⟩ − ∣ 11 ⟩ ) ∣ 0 ⟩ ) \frac{1}{4}|1\rangle(|0\rangle(|00\rangle+|01\rangle+|10\rangle-|11\rangle)|1\rangle+|1\rangle(|00\rangle+|01\rangle+|10\rangle-|11\rangle)|0\rangle) 41∣1⟩(∣0⟩(∣00⟩+∣01⟩+∣10⟩−∣11⟩)∣1⟩+∣1⟩(∣00⟩+∣01⟩+∣10⟩−∣11⟩)∣0⟩)
5. 安全性分析
(1)设Alice和Bob需要 n n n个随机比特的密钥。
Alice和Bob采用上面介绍的量子线路用 4 n 4n 4n个随机数生成 2 n 2n 2n个备选比特。
(2)Alice和Bob从得到的 2 n 2n 2n个备选比特中随机选取 n n n个比特在经典信道上进行比较。
- 若比较结果全部相同 ,则将剩余的 n n n个比特作为密钥使用。
- 若存在不相同的比特(假设量子信道是无噪声的理想信道),则放弃本次密钥分配过程,然后重新进行(1)过程。
例 假设Eve拥有Bob的接收装置和Alice的发送装置。
设计一个Eve从量子信道窃取密钥方案的量子线路,并分析Eve能够成功获取密钥的概率。
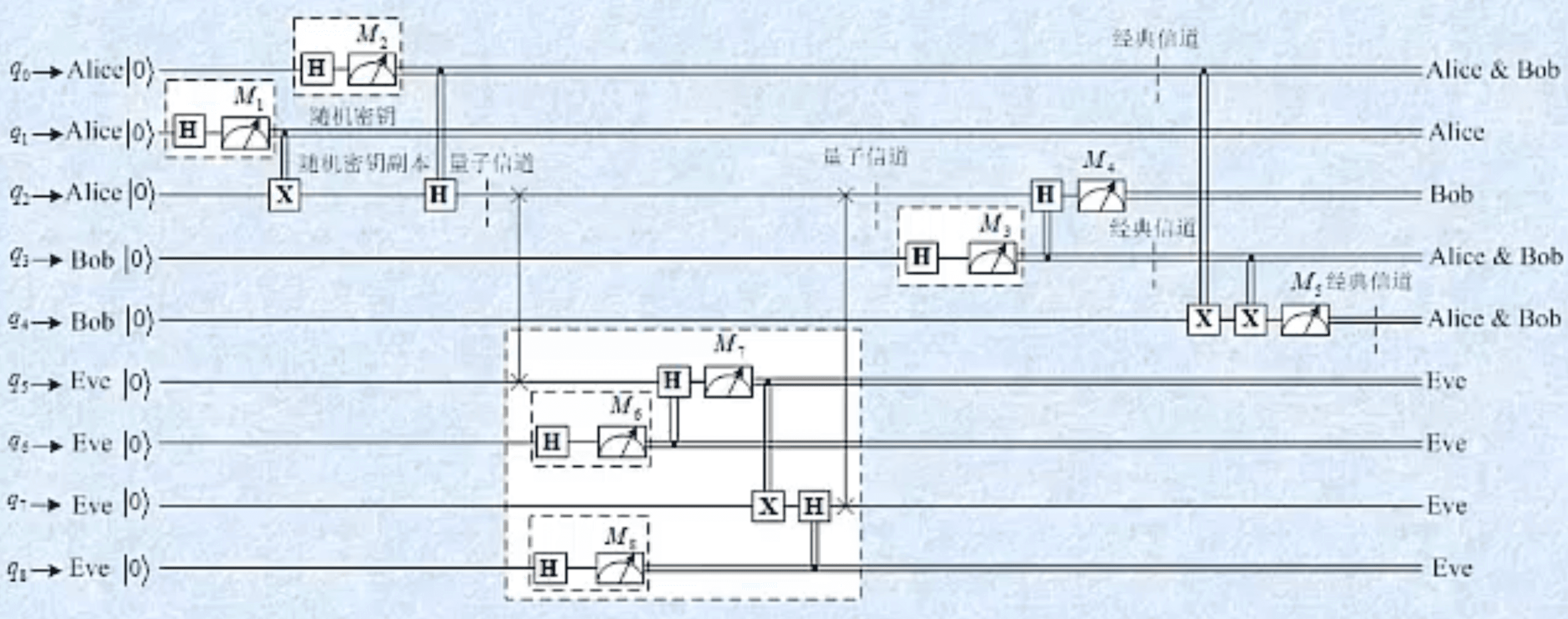
有4种情况Eve可成功窃取密钥,经过仿真结果得出概率
(1) M 2 = M 3 = 0 , M 1 = M 4 = M 7 = 0 M_2=M_3=0, \quad M_1=M_4=M_7=0 M2=M3=0,M1=M4=M7=0
0.6666666667 ∣ 0 ⟩ + 0.47140452 ∣ 64 ⟩ + 0.47140452 ∣ 256 ⟩ + 0.3333333333 ∣ 320 ⟩ = 0.6666666667 ∣ 000000000 ⟩ + 0.47140452 ( ∣ 001000000 ⟩ + ∣ 100000000 ⟩ ) + 0.333333333 ∣ 101000000 ⟩ \begin{aligned} & 0.6666666667|0\rangle + 0.47140452|64\rangle + 0.47140452|256\rangle + 0.3333333333|320\rangle \\ = & 0.6666666667|000000000\rangle \\ & + 0.47140452(|001000000\rangle + |100000000\rangle) \\ & + 0.333333333|101000000\rangle \end{aligned} =0.6666666667∣0⟩+0.47140452∣64⟩+0.47140452∣256⟩+0.3333333333∣320⟩0.6666666667∣000000000⟩+0.47140452(∣001000000⟩+∣100000000⟩)+0.333333333∣101000000⟩
Total evolution probability = 0.0703125
(2) M 2 = M 3 = 1 , M 1 = M 4 = M 7 = 0 M_2=M_3=1, \quad M_1=M_4=M_7=0 M2=M3=1,M1=M4=M7=0
0.3333333333 ∣ 9 ⟩ + 0.47140452 ( ∣ 73 ⟩ + ∣ 265 ⟩ ) + 0.6666666667 ∣ 329 ⟩ = 0.3333333333 ∣ 000001001 ⟩ + 0.47140452 ( ∣ 001001001 ⟩ + ∣ 100001001 ⟩ ) + 0.6666666667 ∣ 101001001 ⟩ \begin{aligned} & 0.3333333333|9\rangle + 0.47140452(|73\rangle + |265\rangle) + 0.6666666667|329\rangle \\ = & 0.3333333333|000001001\rangle \\ & + 0.47140452(|001001001\rangle + |100001001\rangle) \\ & + 0.6666666667|101001001\rangle \end{aligned} =0.3333333333∣9⟩+0.47140452(∣73⟩+∣265⟩)+0.6666666667∣329⟩0.3333333333∣000001001⟩+0.47140452(∣001001001⟩+∣100001001⟩)+0.6666666667∣101001001⟩
Total evolution probability = 0.0703125
(3) M 2 = M 3 = 0 , M 1 = M 4 = M 7 = 1 M_2=M_3=0, \quad M_1=M_4=M_7=1 M2=M3=0,M1=M4=M7=1
0.6666666667 ∣ 38 ⟩ − 0.47140452 ( ∣ 102 ⟩ + ∣ 294 ⟩ ) + 0.333333333 ∣ 358 ⟩ = 0.6666666667 ∣ 000100110 ⟩ − 0.47140452 ( ∣ 001100110 ⟩ + ∣ 100100110 ⟩ ) + 0.333333333 ∣ 101100110 ⟩ \begin{aligned} & 0.6666666667 |38\rangle - 0.47140452 (|102\rangle + |294\rangle) + 0.333333333 |358\rangle \\ &= 0.6666666667 |000100110\rangle \\ &- 0.47140452 (|001100110\rangle + |100100110\rangle) \\ &+ 0.333333333 |101100110\rangle \end{aligned} 0.6666666667∣38⟩−0.47140452(∣102⟩+∣294⟩)+0.333333333∣358⟩=0.6666666667∣000100110⟩−0.47140452(∣001100110⟩+∣100100110⟩)+0.333333333∣101100110⟩
Total evolution probability = 0.0703125 = 0.0703125 =0.0703125
(4) M 2 = M 3 = 1 , M 1 = M 4 = M 7 = 1 M_2=M_3=1, \quad M_1=M_4=M_7=1 M2=M3=1,M1=M4=M7=1
0.333333333 ∣ 47 ⟩ − 0.47140452 ( ∣ 111 ⟩ + ∣ 303 ⟩ ) + 0.666666667 ∣ 367 ⟩ = 0.333333333 ∣ 000101111 ⟩ − 0.47140452 ( ∣ 001101111 ⟩ + ∣ 100101111 ⟩ ) + 0.666666667 ∣ 101101111 ⟩ \begin{aligned} & 0.333333333 |47\rangle - 0.47140452 (|111\rangle + |303\rangle) + 0.666666667 |367\rangle \\ &= 0.333333333 |000101111\rangle \\ &- 0.47140452 (|001101111\rangle + |100101111\rangle) \\ &+ 0.666666667 |101101111\rangle \end{aligned} 0.333333333∣47⟩−0.47140452(∣111⟩+∣303⟩)+0.666666667∣367⟩=0.333333333∣000101111⟩−0.47140452(∣001101111⟩+∣100101111⟩)+0.666666667∣101101111⟩
Total evolution probability = 0.0703125 = 0.0703125 =0.0703125
将上述4个概率相加得到Eve 成功窃取密钥,而未被Alice 和Bob 发现的概率为
p = 4 × 0.0703125 = 0.28125 p = 4 \times 0.0703125 = 0.28125 p=4×0.0703125=0.28125
若Alice 和Bob 用10个备选比特验证,而都无法发现Eve 成功窃取密钥的概率为
p 10 ≈ 3 × 10 − 6 p^{10} \approx 3 \times 10^{-6} p10≈3×10−6
若Alice 和Bob 用100个备选比特验证,而都无法发现Eve 成功窃取密钥的概率为
p 100 ≈ 8 × 10 − 56 p^{100} \approx 8 \times 10^{-56} p100≈8×10−56
参考文献
高岩《量子线路》