注:本文是之前记录的草稿,估计短期内没有时间写文章。先发出来,以后时机合适再整理重新发布。
量子密钥分发-B92 协议
B92协议是 BB84 的"精简改进版",由 Charles Bennett(也是 BB84 的共同发明人)在 1992 年提出。本文介绍了B92 协议的原理架构、量子态演变和安全性分析。
1. B92协议表示0和1的方案
(1)以50%的概率用状态 ∣0⟩|0\rangle∣0⟩ 表示0。
(2)以50%的概率用状态 ∣0⟩+∣1⟩2\frac{|0\rangle+|1\rangle}{\sqrt{2}}2 ∣0⟩+∣1⟩ 表示1。
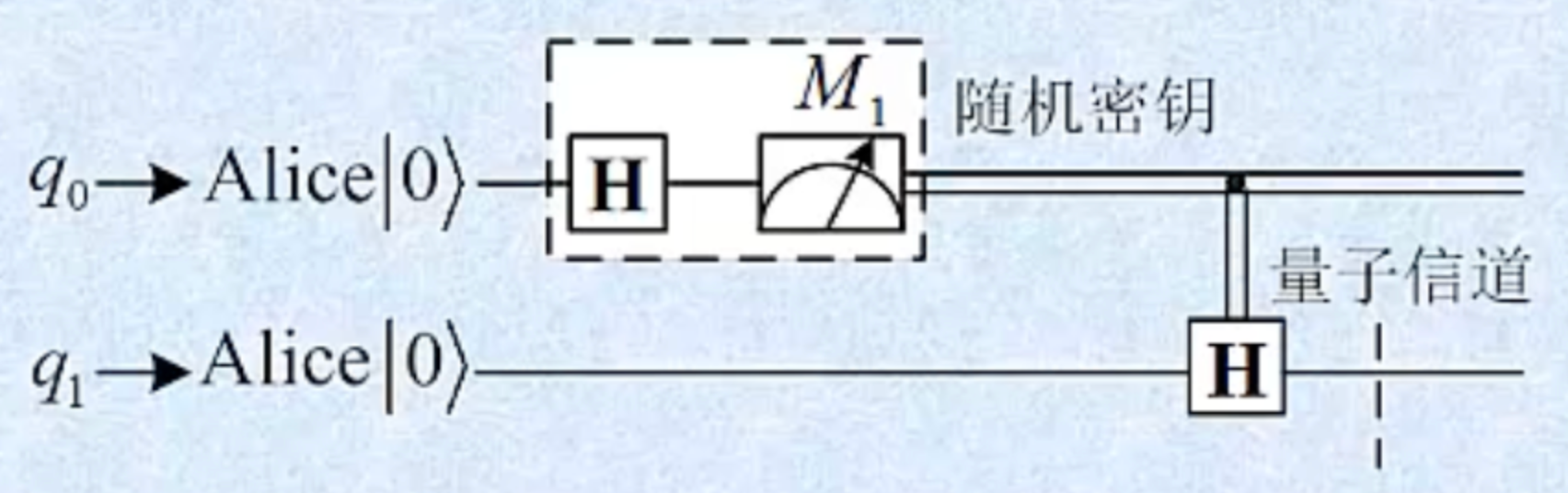
2. B92协议线路模型
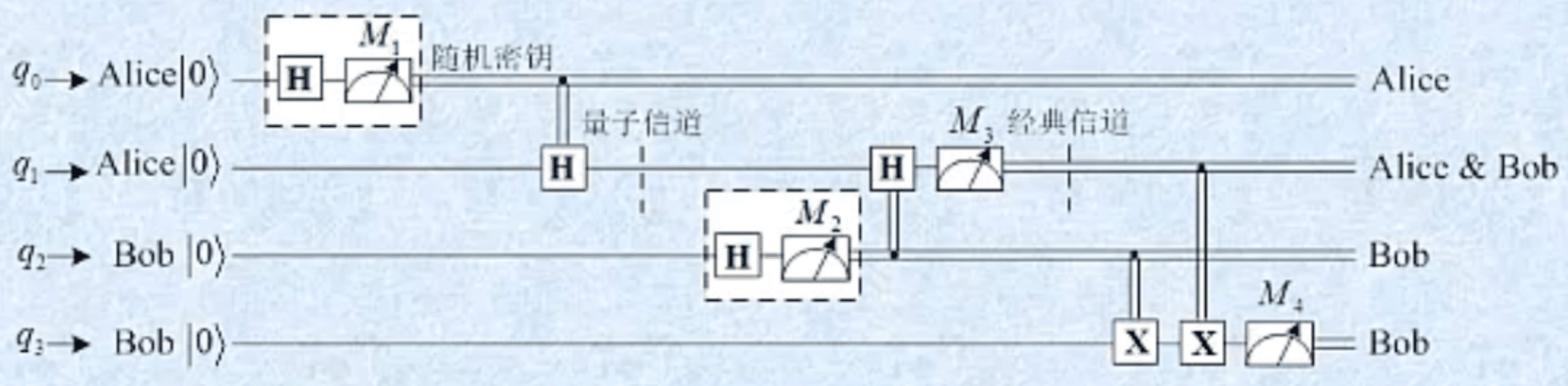
当M3=1M_3=1M3=1时,M1M_1M1是M2M_2M2的非。即M1 != M2。
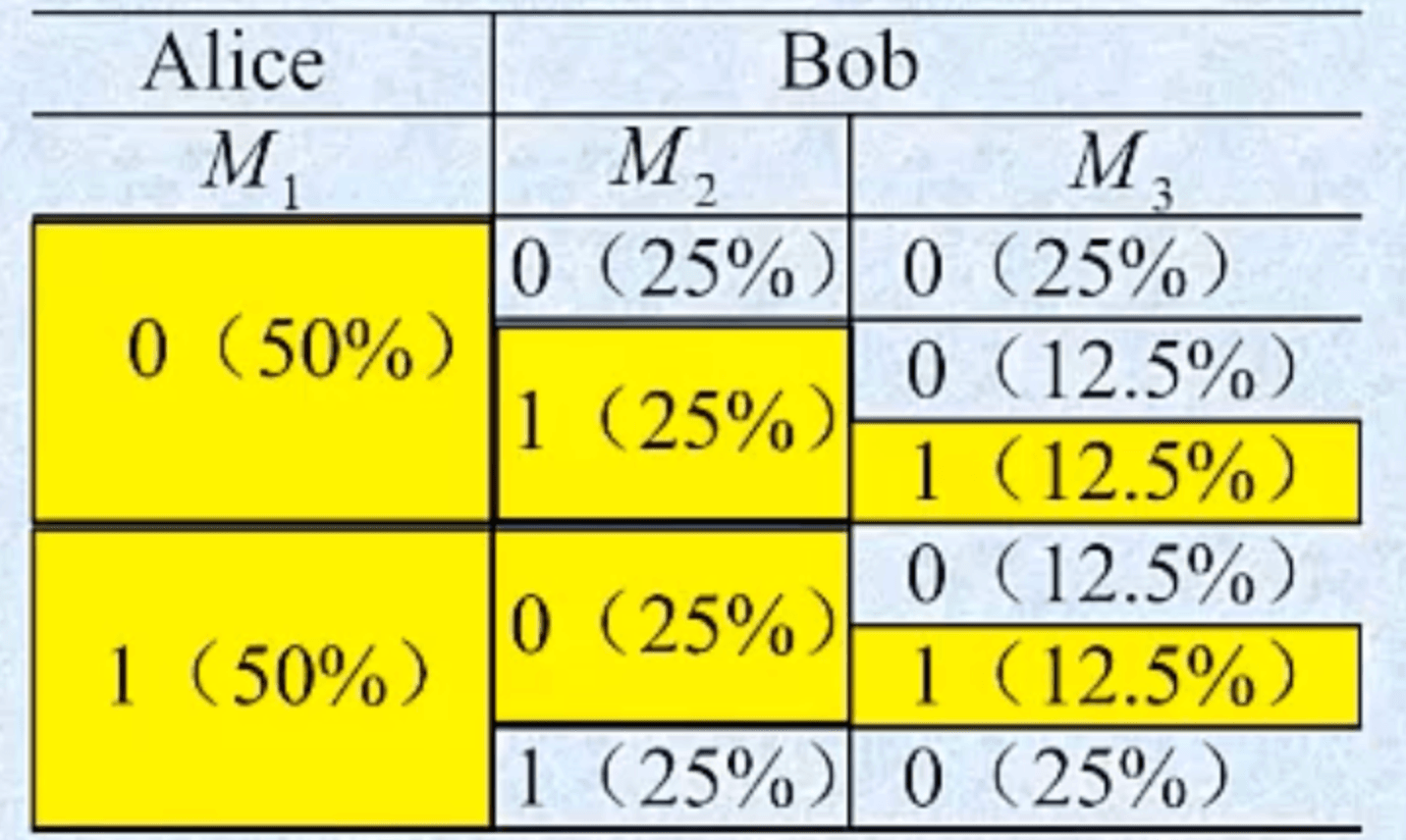
只取 M3=1M_3=1M3=1时的测量结果,丢掉M3=0M_3=0M3=0时的测量结果。这时,M4=M1M_4=M_1M4=M1。
3. 状态演化分析
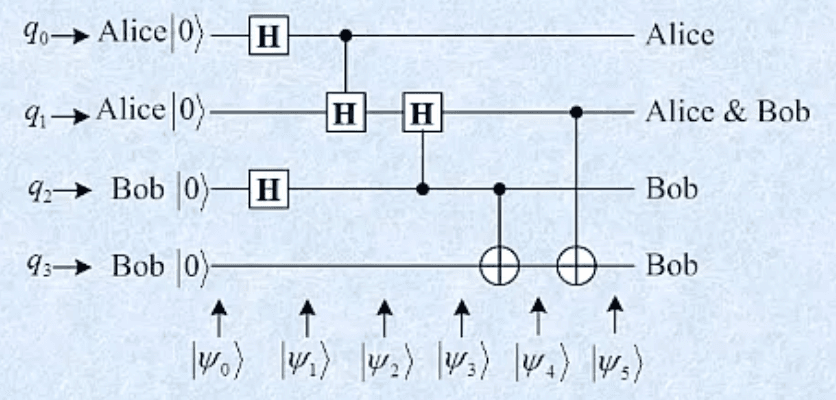
q3≺q2≺q1≺q0q_3 \prec q_2 \prec q_1 \prec q_0q3≺q2≺q1≺q0
∣ψ0⟩=∣0000⟩|\psi_0\rangle = |0000\rangle∣ψ0⟩=∣0000⟩
∣ψ1⟩=∣0⟩∣0⟩+∣1⟩2∣0⟩∣0⟩+∣1⟩2=∣0⟩∣0⟩+∣1⟩2∣00⟩+∣01⟩2\begin{aligned} |\psi_1\rangle &= |0\rangle \frac{|0\rangle+|1\rangle}{\sqrt{2}} |0\rangle \frac{|0\rangle+|1\rangle}{\sqrt{2}} = |0\rangle \frac{|0\rangle+|1\rangle}{\sqrt{2}} \frac{|00\rangle+|01\rangle}{\sqrt{2}} \end{aligned}∣ψ1⟩=∣0⟩2 ∣0⟩+∣1⟩∣0⟩2 ∣0⟩+∣1⟩=∣0⟩2 ∣0⟩+∣1⟩2 ∣00⟩+∣01⟩
∣ψ2⟩=∣0⟩∣0⟩+∣1⟩2∣00⟩+∣0⟩+∣1⟩2∣1⟩2=∣0⟩∣0⟩+∣1⟩22∣00⟩+∣01⟩+∣11⟩2=∣0⟩2∣000⟩+∣001⟩+∣011⟩+2∣100⟩+∣101⟩+∣111⟩22\begin{aligned} |\psi_{2}\rangle &= |0\rangle \frac{|0\rangle+|1\rangle}{\sqrt{2}} \frac{|00\rangle+\frac{|0\rangle+|1\rangle}{\sqrt{2}}|1\rangle}{\sqrt{2}} \\ &= |0\rangle \frac{|0\rangle+|1\rangle}{\sqrt{2}} \frac{\sqrt{2}|00\rangle+|01\rangle+|11\rangle}{2} \\ &= |0\rangle \frac{\sqrt{2}|000\rangle+|001\rangle+|011\rangle+\sqrt{2}|100\rangle+|101\rangle+|111\rangle}{2 \sqrt{2}} \end{aligned}∣ψ2⟩=∣0⟩2 ∣0⟩+∣1⟩2 ∣00⟩+2 ∣0⟩+∣1⟩∣1⟩=∣0⟩2 ∣0⟩+∣1⟩22 ∣00⟩+∣01⟩+∣11⟩=∣0⟩22 2 ∣000⟩+∣001⟩+∣011⟩+2 ∣100⟩+∣101⟩+∣111⟩
∣ψ3⟩=∣0⟩2∣000⟩+∣001⟩+∣011⟩+2∣1⟩∣0⟩+∣1⟩2∣0⟩+∣1⟩∣0⟩+∣1⟩2∣1⟩+∣1⟩∣0⟩−∣1⟩2∣1⟩22=122(2∣0000⟩+∣0001⟩+∣0011⟩+∣0100⟩+2∣0101⟩+∣0110⟩)\begin{aligned} |\psi_{3}\rangle &= |0\rangle \frac{\sqrt{2}|000\rangle+|001\rangle+|011\rangle+\sqrt{2}|1\rangle \frac{|0\rangle+|1\rangle}{\sqrt{2}}|0\rangle+|1\rangle \frac{|0\rangle+|1\rangle}{\sqrt{2}}|1\rangle+|1\rangle \frac{|0\rangle-|1\rangle}{\sqrt{2}}|1\rangle}{2 \sqrt{2}} \\ &= \frac{1}{2 \sqrt{2}} (\sqrt{2}|0000\rangle+|0001\rangle+|0011\rangle+|0100\rangle+\sqrt{2}|0101\rangle+|0110\rangle) \end{aligned}∣ψ3⟩=∣0⟩22 2 ∣000⟩+∣001⟩+∣011⟩+2 ∣1⟩2 ∣0⟩+∣1⟩∣0⟩+∣1⟩2 ∣0⟩+∣1⟩∣1⟩+∣1⟩2 ∣0⟩−∣1⟩∣1⟩=22 1(2 ∣0000⟩+∣0001⟩+∣0011⟩+∣0100⟩+2 ∣0101⟩+∣0110⟩)
∣ψ4⟩=122(2∣0000⟩+∣0001⟩+∣0011⟩+∣1100⟩+2∣1101⟩+∣1110⟩)|\psi_4\rangle = \frac{1}{2 \sqrt{2}} (\sqrt{2}|0000\rangle+|0001\rangle+|0011\rangle+|1100\rangle+\sqrt{2}|1101\rangle+|1110\rangle)∣ψ4⟩=22 1(2 ∣0000⟩+∣0001⟩+∣0011⟩+∣1100⟩+2 ∣1101⟩+∣1110⟩)
∣ψ5⟩=122(2∣0000⟩+∣0001⟩+∣1011⟩+∣1100⟩+2∣1101⟩+∣0110⟩)=122(2∣0000⟩+∣0001⟩+∣1100⟩+2∣1101⟩)+122(∣0110⟩+∣1011⟩)\begin{aligned} |\psi_5\rangle &= \frac{1}{2 \sqrt{2}} (\sqrt{2}|0000\rangle+|0001\rangle+|1011\rangle+|1100\rangle+\sqrt{2}|1101\rangle+|0110\rangle) \\ &= \frac{1}{2 \sqrt{2}} (\sqrt{2}|0000\rangle+|0001\rangle+|1100\rangle+\sqrt{2}|1101\rangle) + \frac{1}{2 \sqrt{2}} (|0110\rangle+|1011\rangle) \end{aligned}∣ψ5⟩=22 1(2 ∣0000⟩+∣0001⟩+∣1011⟩+∣1100⟩+2 ∣1101⟩+∣0110⟩)=22 1(2 ∣0000⟩+∣0001⟩+∣1100⟩+2 ∣1101⟩)+22 1(∣0110⟩+∣1011⟩)
- 当测量指示器 q1=1q_1=1q1=1 时,q0q_0q0 和 q3q_3q3 的结果为 00、11 。概率 25%
- 当测量指示器 q1=0q_1=0q1=0 时,q0q_0q0 和 q3q_3q3 的结果为 00、01、10、11 。概率 75%
4. 安全性分析
(1)设Alice和Bob需要nnn个随机比特的密钥。
Alice和Bob采用上面介绍的量子线路用8n8n8n个随机数产生2n2n2n个备选比特。
(2)Alice和Bob从得到的2n2n2n个备选比特中随机选取nnn个比特在经典信道上进行比较。
- 若比较结果全部相同,则将剩余的nnn个比特作为密钥使用。
- 若存在不相同的比特(假设量子信道是无噪声的理想信道),则放弃本次密钥分配过程,然后重新进行(1)过程。
例\] 假设Eve拥有Bob的接收装置和Alice的发送装置。设计一个Eve从量子信道窃取密钥方案的量子线路,并分析Eve能够成功获取密钥的概率。 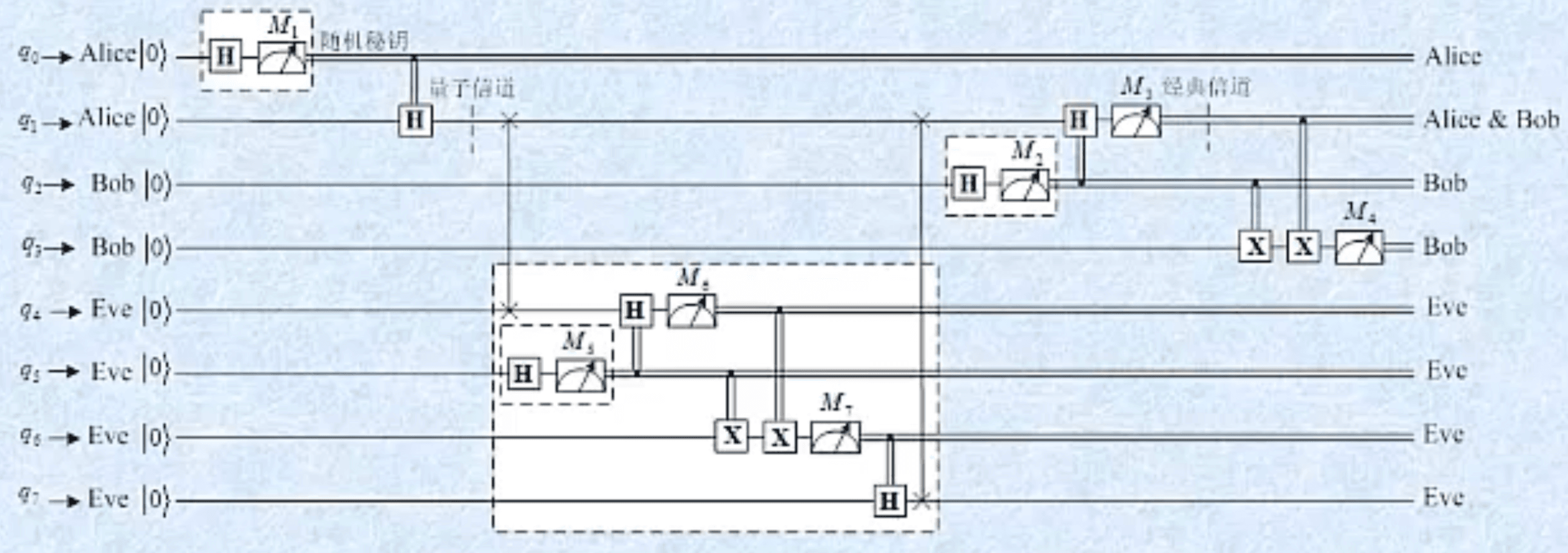 有2种情况Eve可成功窃取密钥 (1)M6=M3=1,M7=M1=M4=0;M5=M2=1M_6=M_3=1, \\quad M_7=M_1=M_4=0;\\quad M_5=M_2=1M6=M3=1,M7=M1=M4=0;M5=M2=1 (2)M6=M3=1,M7=M1=M4=1;M5=M2=0M_6=M_3=1, \\quad M_7=M_1=M_4=1;\\quad M_5=M_2=0M6=M3=1,M7=M1=M4=1;M5=M2=0 Eve成功窃取密钥而未被Alice和Bob发现的概率为 p=2×0.03125=0.0625p = 2 \\times 0.03125 = 0.0625p=2×0.03125=0.0625 若Alice和Bob用10个备选比特验证,而都无法发现Eve成功窃取密钥的概率为 p10≈9×10−13p\^{10} \\approx 9 \\times 10\^{-13}p10≈9×10−13 若Alice和Bob用100个备选比特验证,而都无法发现Eve成功窃取密钥的概率为 p100≈4×10−121p\^{100} \\approx 4 \\times 10\^{-121}p100≈4×10−121 ## 5. BB84 与 B92 协议的比较 | 比较项目 | BB84 协议 | B92 协议 | |:---------------------------|:----------------------------------------------------------------------------|:-------------------------------------------------------------------| | **密钥产生效率** | 50%50\\%50% | 25%25\\%25% | | **Eve 成功窃听单个随机数的概率 (ppp)** | p=4×0.0703125=0.28125p = 4 \\times 0.0703125 = 0.28125p=4×0.0703125=0.28125 | p=2×0.03125=0.0625p = 2 \\times 0.03125 = 0.0625p=2×0.03125=0.0625 | | **安全性特点** | 窃听成功率较高,但效率也较高 | 窃听成功率较低,安全性相对更强,但效率较低 | ## 参考文献 高岩《量子线路》