量子计算 量子密钥分发（QKD）

注：本文是之前写的草稿，估计短期内没有时间写文章。先发出来，以后时机合适再整理重新发布。

量子密钥分发（QKD）

• [0 前言](#0 前言)
• [1. 量子随机密钥发生器（真随机数发生器）](#1. 量子随机密钥发生器（真随机数发生器）)
• [2 量子线路与状态](#2 量子线路与状态)
• • [2.1 初始状态 ∣ ψ 0 ⟩ |\psi_0\rangle ∣ψ0⟩：系统初始化](#2.1 初始状态 ∣ ψ 0 ⟩ |\psi_0\rangle ∣ψ0⟩：系统初始化)
  • [2.2 中间状态 ∣ ψ 1 ⟩ |\psi_1\rangle ∣ψ1⟩：引入叠加态](#2.2 中间状态 ∣ ψ 1 ⟩ |\psi_1\rangle ∣ψ1⟩：引入叠加态)
  • [2.3 最终状态 ∣ ψ 2 ⟩ |\psi_2\rangle ∣ψ2⟩：产生量子纠缠](#2.3 最终状态 ∣ ψ 2 ⟩ |\psi_2\rangle ∣ψ2⟩：产生量子纠缠)
• [3 量子态张量积的完整推导过程](#3 量子态张量积的完整推导过程)
• • [3.1 定义基础向量](#3.1 定义基础向量)
  • [3.2 计算组合态 ∣ ψ 0 ⟩ = ∣ 0 ⟩ ⊗ ∣ 0 ⟩ |\psi_0\rangle = |0\rangle \otimes |0\rangle ∣ψ0⟩=∣0⟩⊗∣0⟩](#3.2 计算组合态 ∣ ψ 0 ⟩ = ∣ 0 ⟩ ⊗ ∣ 0 ⟩ |\psi_0\rangle = |0\rangle \otimes |0\rangle ∣ψ0⟩=∣0⟩⊗∣0⟩)
  • [3.3 经过 H 门后的状态 ∣ ψ 1 ⟩ |\psi_1\rangle ∣ψ1⟩](#3.3 经过 H 门后的状态 ∣ ψ 1 ⟩ |\psi_1\rangle ∣ψ1⟩)
  • [3.4 经过 CNOT 门后的状态 ∣ ψ 2 ⟩ |\psi_2\rangle ∣ψ2⟩](#3.4 经过 CNOT 门后的状态 ∣ ψ 2 ⟩ |\psi_2\rangle ∣ψ2⟩)
• [4 证明：贝尔态 ∣ Φ + ⟩ = ∣ 00 ⟩ + ∣ 11 ⟩ 2 |\Phi^+\rangle = \frac{|00\rangle + |11\rangle}{\sqrt{2}} ∣Φ+⟩=2 ∣00⟩+∣11⟩ 是不可分离的纠缠态](#4 证明：贝尔态 ∣ Φ + ⟩ = ∣ 00 ⟩ + ∣ 11 ⟩ 2 |\Phi^+\rangle = \frac{|00\rangle + |11\rangle}{\sqrt{2}} ∣Φ+⟩=2 ∣00⟩+∣11⟩ 是不可分离的纠缠态)
• • [4.1 假设量子态可被拆分](#4.1 假设量子态可被拆分)
  • [4.2 与贝尔态进行对比](#4.2 与贝尔态进行对比)
  • [4.3 发现矛盾](#4.3 发现矛盾)
  • [4.4 结论](#4.4 结论)
• [5 监听过程量子态演变](#5 监听过程量子态演变)
• • 量子态序列分析
• 参考文献

0 前言

本文介绍了量子密钥分发的基本过程，以及一些基础知识比如叠加态、纠缠态、张量积、贝尔态以及量子加密通信中的量子态演变。

1. 量子随机密钥发生器（真随机数发生器）

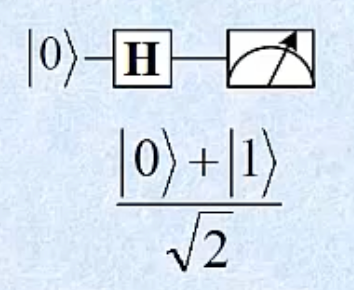
∣ 0 ⟩ ⟶ H ⟶ M |0\rangle \longrightarrow \boxed{\text{H}} \longrightarrow \text{M} ∣0⟩⟶H⟶M

∣ 0 ⟩ + ∣ 1 ⟩ 2 \frac{|0\rangle+|1\rangle}{\sqrt{2}} 2 ∣0⟩+∣1⟩

• 测量 将各以 50% 的概率得到结果 0 和 1。
• 该线路执行 100 次，可生成由 100 位二进制随机数构成密钥。
• 由于该随机密钥是基于物理系统的酉演化性质，称为物理原理保障的随机密钥。

2 量子线路与状态

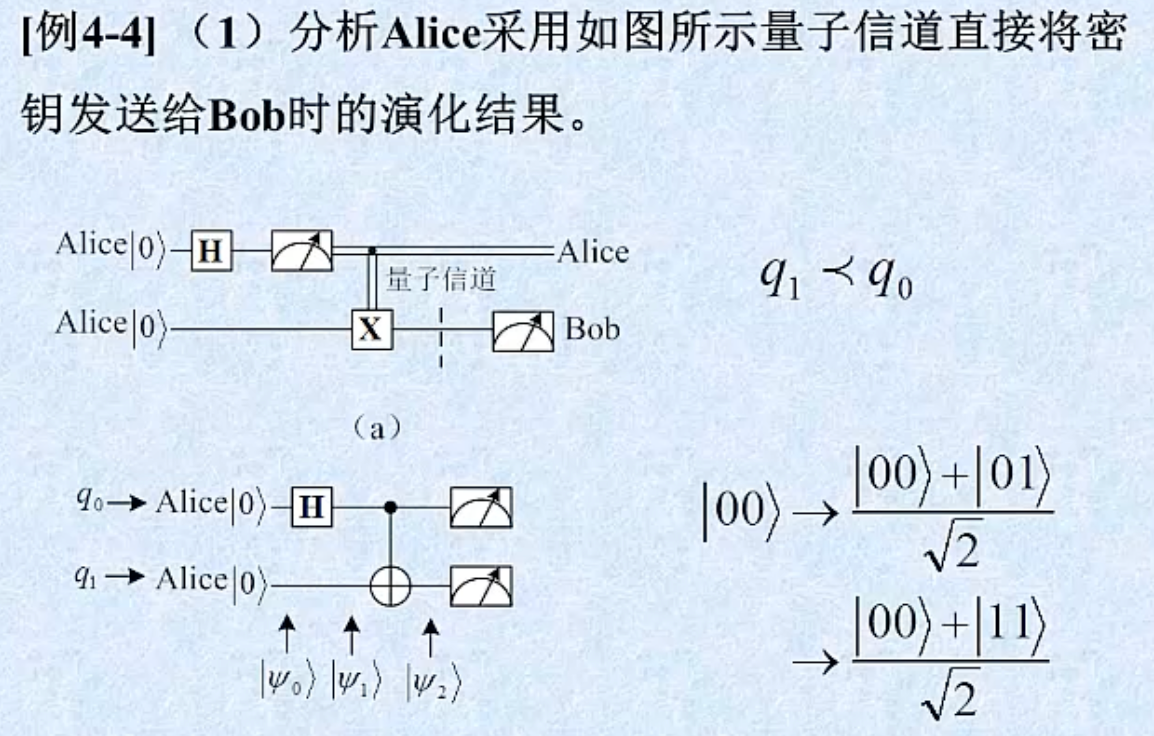
这张图展示的是量子计算中一个非常经典的过程：利用 Hadamard 门（H 门）和 CNOT 门将两个处于基础态的量子比特转变为"贝尔态"（Bell State），即最大纠缠态。

我们可以按照图中标记的 ∣ ψ 0 ⟩ , ∣ ψ 1 ⟩ , ∣ ψ 2 ⟩ |\psi_0\rangle, |\psi_1\rangle, |\psi_2\rangle ∣ψ0⟩,∣ψ1⟩,∣ψ2⟩ 三个阶段来拆解这个量子态演化的过程：

2.1 初始状态 ∣ ψ 0 ⟩ |\psi_0\rangle ∣ψ0⟩：系统初始化

在最左侧，两个量子比特 q 0 q_0 q0 和 q 1 q_1 q1 都被初始化在计算基态 ∣ 0 ⟩ |0\rangle ∣0⟩。

• 数学表示： ∣ ψ 0 ⟩ = ∣ 0 ⟩ ⊗ ∣ 0 ⟩ = ∣ 00 ⟩ |\psi_0\rangle = |0\rangle \otimes |0\rangle = |00\rangle ∣ψ0⟩=∣0⟩⊗∣0⟩=∣00⟩
  （此时两个比特是相互独立的，没有任何关联。）

2.2 中间状态 ∣ ψ 1 ⟩ |\psi_1\rangle ∣ψ1⟩：引入叠加态

量子比特 q 0 q_0 q0 经过了一个 Hadamard 门 (H) 。H 门的作用是将 ∣ 0 ⟩ |0\rangle ∣0⟩ 变为等概率叠加态 ∣ 0 ⟩ + ∣ 1 ⟩ 2 \frac{|0\rangle + |1\rangle}{\sqrt{2}} 2 ∣0⟩+∣1⟩，而 q 1 q_1 q1 保持不变。

• 数学表示：
  ∣ ψ 1 ⟩ = ( H ∣ 0 ⟩ ) ⊗ ∣ 0 ⟩ = ∣ 0 ⟩ + ∣ 1 ⟩ 2 ⊗ ∣ 0 ⟩ = ∣ 00 ⟩ + ∣ 10 ⟩ 2 |\psi_1\rangle = (H|0\rangle) \otimes |0\rangle = \frac{|0\rangle + |1\rangle}{\sqrt{2}} \otimes |0\rangle = \frac{|00\rangle + |10\rangle}{\sqrt{2}} ∣ψ1⟩=(H∣0⟩)⊗∣0⟩=2 ∣0⟩+∣1⟩⊗∣0⟩=2 ∣00⟩+∣10⟩
  （这一步让第一个比特处于"既是 0 又是 1"的叠加状态，但两个比特之间仍未纠缠。）

2.3 最终状态 ∣ ψ 2 ⟩ |\psi_2\rangle ∣ψ2⟩：产生量子纠缠

接下来，两个比特共同经过一个 CNOT 门 （受控非门）。图中 q 0 q_0 q0 上的实心点是控制位 ， q 1 q_1 q1 上的圆圈十字是目标位。

• CNOT 规则： 如果控制位是 ∣ 1 ⟩ |1\rangle ∣1⟩，则翻转目标位；如果控制位是 ∣ 0 ⟩ |0\rangle ∣0⟩，则目标位保持不变。
• 演化过程：
  • 对于分量 ∣ 00 ⟩ |00\rangle ∣00⟩：控制位是 0，目标位不变，结果仍为 ∣ 00 ⟩ |00\rangle ∣00⟩。
  • 对于分量 ∣ 10 ⟩ |10\rangle ∣10⟩：控制位是 1，目标位从 0 翻转为 1，结果变为 ∣ 11 ⟩ |11\rangle ∣11⟩。
• 数学表示：
  ∣ ψ 2 ⟩ = ∣ 00 ⟩ + ∣ 11 ⟩ 2 |\psi_2\rangle = \frac{|00\rangle + |11\rangle}{\sqrt{2}} ∣ψ2⟩=2 ∣00⟩+∣11⟩
  （这就是著名的贝尔态 Φ + \Phi^+ Φ+。此时，两个比特进入了深度纠缠：如果你测量发现第一个比特是 0，第二个比特瞬间也会确定为 0；反之亦然。）

总的来说，右侧的公式简洁地概括了这个逻辑：

1. 第一行 ： ∣ 00 ⟩ → ∣ 00 ⟩ + ∣ 01 ⟩ 2 |00\rangle \rightarrow \frac{|00\rangle + |01\rangle}{\sqrt{2}} ∣00⟩→2 ∣00⟩+∣01⟩ （这行公式在图中其实略有出入，标准解释应为 q 0 q_0 q0 变为叠加态后的状态）。
2. 第二行 ：展示了最终结果 ∣ 00 ⟩ + ∣ 11 ⟩ 2 \frac{|00\rangle + |11\rangle}{\sqrt{2}} 2 ∣00⟩+∣11⟩，即通过 CNOT 门完成了从叠加到纠缠的跨越。

3 量子态张量积的完整推导过程

在量子计算中，张量积 ( ⊗ \otimes ⊗) 是将多个独立的量子对比特空间组合成一个更大复合系统的数学工具。以下是详细的步骤推导：

3.1 定义基础向量

假设我们有两个独立的量子比特 ∣ q 0 ⟩ |q_0\rangle ∣q0⟩ 和 ∣ q 1 ⟩ |q_1\rangle ∣q1⟩。它们在计算基下的列向量表示为：
∣ 0 ⟩ = [ 1 0 ] , ∣ 1 ⟩ = [ 0 1 ] |0\rangle = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \quad |1\rangle = \begin{bmatrix} 0 \\ 1 \end{bmatrix} ∣0⟩=[10],∣1⟩=[01]

3.2 计算组合态 ∣ ψ 0 ⟩ = ∣ 0 ⟩ ⊗ ∣ 0 ⟩ |\psi_0\rangle = |0\rangle \otimes |0\rangle ∣ψ0⟩=∣0⟩⊗∣0⟩

当两个比特都处于 ∣ 0 ⟩ |0\rangle ∣0⟩ 态时，复合系统通过克罗内克积 (Kronecker Product) 计算：
∣ 00 ⟩ = [ 1 0 ] ⊗ [ 1 0 ] = [ 1 ⋅ [ 1 0 ] 0 ⋅ [ 1 0 ] ] = [ 1 0 0 0 ] |00\rangle = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \otimes \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 \cdot \begin{bmatrix} 1 \\ 0 \end{bmatrix} \\ 0 \cdot \begin{bmatrix} 1 \\ 0 \end{bmatrix} \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} ∣00⟩=[10]⊗[10]= 1⋅[10]0⋅[10] = 1000

这个 4 维向量的第一个分量为 1，代表系统处于 2 2 = 4 2^2=4 22=4 种可能状态中的第一种。

3.3 经过 H 门后的状态 ∣ ψ 1 ⟩ |\psi_1\rangle ∣ψ1⟩

量子态 ∣ 0 ⟩ |0\rangle ∣0⟩ 经过 Hadamard 门的矩阵变换

1. 计算基中 ∣ 0 ⟩ |0\rangle ∣0⟩ 的列向量表示

在计算基 { ∣ 0 ⟩ , ∣ 1 ⟩ } \{|0\rangle, |1\rangle\} {∣0⟩,∣1⟩} 下：

∣ 0 ⟩ = [ 1 0 ] |0\rangle = \begin{bmatrix} 1 \\ 0 \end{bmatrix} ∣0⟩=[10]

2. Hadamard 门的矩阵形式

H = 1 2 [ 1 1 1 − 1 ] H = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} H=2 1[111−1]

3. Hadamard 门作用于 ∣ 0 ⟩ |0\rangle ∣0⟩

H ∣ 0 ⟩ = 1 2 [ 1 1 1 − 1 ] [ 1 0 ] H|0\rangle = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} H∣0⟩=2 1[111−1][10]

逐行计算：

• 第一行： 1 ⋅ 1 + 1 ⋅ 0 = 1 1 \cdot 1 + 1 \cdot 0 = 1 1⋅1+1⋅0=1
• 第二行： 1 ⋅ 1 + ( − 1 ) ⋅ 0 = 1 1 \cdot 1 + (-1) \cdot 0 = 1 1⋅1+(−1)⋅0=1

因此：

H ∣ 0 ⟩ = 1 2 [ 1 1 ] H|0\rangle = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix} H∣0⟩=2 1[11]

4. 用 Dirac 记号表示结果

1 2 [ 1 1 ] = ∣ 0 ⟩ + ∣ 1 ⟩ 2 = ∣ + ⟩ \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix} =\frac{|0\rangle + |1\rangle}{\sqrt{2}} = |+\rangle 2 1[11]=2 ∣0⟩+∣1⟩=∣+⟩

5. 同理可得

H ∣ 1 ⟩ = ∣ 0 ⟩ − ∣ 1 ⟩ 2 = ∣ − ⟩ H|1\rangle = \frac{|0\rangle - |1\rangle}{\sqrt{2}} = |-\rangle H∣1⟩=2 ∣0⟩−∣1⟩=∣−⟩

在电路中， q 0 q_0 q0 经过 Hadamard 门变为 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) 2 1(∣0⟩+∣1⟩)，而 q 1 q_1 q1 保持 ∣ 0 ⟩ |0\rangle ∣0⟩。

此时整体状态为：
∣ ψ 1 ⟩ = ( 1 2 [ 1 1 ] ) ⊗ [ 1 0 ] |\psi_1\rangle = \left( \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix} \right) \otimes \begin{bmatrix} 1 \\ 0 \end{bmatrix} ∣ψ1⟩=(2 1[11])⊗[10]

展开计算：
∣ ψ 1 ⟩ = 1 2 [ 1 ⋅ 1 1 ⋅ 0 1 ⋅ 1 1 ⋅ 0 ] = 1 2 [ 1 0 1 0 ] |\psi_1\rangle = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \cdot 1 \\ 1 \cdot 0 \\ 1 \cdot 1 \\ 1 \cdot 0 \end{bmatrix} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 0 \\ 1 \\ 0 \end{bmatrix} ∣ψ1⟩=2 1 1⋅11⋅01⋅11⋅0 =2 1 1010

对应的狄拉克符号为： 1 2 ( ∣ 00 ⟩ + ∣ 10 ⟩ ) \frac{1}{\sqrt{2}}(|00\rangle + |10\rangle) 2 1(∣00⟩+∣10⟩)。

3.4 经过 CNOT 门后的状态 ∣ ψ 2 ⟩ |\psi_2\rangle ∣ψ2⟩

CNOT 门作用在 4 维复合空间上。其矩阵 C C C 与状态向量 ∣ ψ 1 ⟩ |\psi_1\rangle ∣ψ1⟩ 相乘：
∣ ψ 2 ⟩ = [ 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 ] 1 2 [ 1 0 1 0 ] |\psi_2\rangle = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix} \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 0 \\ 1 \\ 0 \end{bmatrix} ∣ψ2⟩= 1000010000010010 2 1 1010

矩阵乘法过程：

• 第一行： 1 ⋅ 1 + 0 ⋅ 0 + 0 ⋅ 1 + 0 ⋅ 0 = 1 1\cdot1 + 0\cdot0 + 0\cdot1 + 0\cdot0 = 1 1⋅1+0⋅0+0⋅1+0⋅0=1
• 第二行： 0 ⋅ 1 + 1 ⋅ 0 + 0 ⋅ 1 + 0 ⋅ 0 = 0 0\cdot1 + 1\cdot0 + 0\cdot1 + 0\cdot0 = 0 0⋅1+1⋅0+0⋅1+0⋅0=0
• 第三行： 0 ⋅ 1 + 0 ⋅ 0 + 0 ⋅ 1 + 1 ⋅ 0 = 0 0\cdot1 + 0\cdot0 + 0\cdot1 + 1\cdot0 = 0 0⋅1+0⋅0+0⋅1+1⋅0=0
• 第四行： 0 ⋅ 1 + 0 ⋅ 0 + 1 ⋅ 1 + 0 ⋅ 0 = 1 0\cdot1 + 0\cdot0 + 1\cdot1 + 0\cdot0 = 1 0⋅1+0⋅0+1⋅1+0⋅0=1

最终得到：
∣ ψ 2 ⟩ = 1 2 [ 1 0 0 1 ] = ∣ 00 ⟩ + ∣ 11 ⟩ 2 |\psi_2\rangle = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 0 \\ 0 \\ 1 \end{bmatrix} = \frac{|00\rangle + |11\rangle}{\sqrt{2}} ∣ψ2⟩=2 1 1001 =2 ∣00⟩+∣11⟩

4 证明：贝尔态 ∣ Φ + ⟩ = ∣ 00 ⟩ + ∣ 11 ⟩ 2 |\Phi^+\rangle = \frac{|00\rangle + |11\rangle}{\sqrt{2}} ∣Φ+⟩=2 ∣00⟩+∣11⟩ 是不可分离的纠缠态

4.1 假设量子态可被拆分

即假设这个态可以写成两个独立量子比特状态的张量积。

设第一个比特的状态为 ∣ α ⟩ = a ∣ 0 ⟩ + b ∣ 1 ⟩ |\alpha\rangle = a|0\rangle + b|1\rangle ∣α⟩=a∣0⟩+b∣1⟩，第二个比特的状态为 ∣ β ⟩ = c ∣ 0 ⟩ + d ∣ 1 ⟩ |\beta\rangle = c|0\rangle + d|1\rangle ∣β⟩=c∣0⟩+d∣1⟩。那么它们的张量积展开为：
∣ α ⟩ ⊗ ∣ β ⟩ = ( a ∣ 0 ⟩ + b ∣ 1 ⟩ ) ⊗ ( c ∣ 0 ⟩ + d ∣ 1 ⟩ ) |\alpha\rangle \otimes |\beta\rangle = (a|0\rangle + b|1\rangle) \otimes (c|0\rangle + d|1\rangle) ∣α⟩⊗∣β⟩=(a∣0⟩+b∣1⟩)⊗(c∣0⟩+d∣1⟩)
= a c ∣ 00 ⟩ + a d ∣ 01 ⟩ + b c ∣ 10 ⟩ + b d ∣ 11 ⟩ = ac|00\rangle + ad|01\rangle + bc|10\rangle + bd|11\rangle =ac∣00⟩+ad∣01⟩+bc∣10⟩+bd∣11⟩

4.2 与贝尔态进行对比

现在我们将这个展开式与我们要证明的贝尔态对比：
1 2 ∣ 00 ⟩ + 0 ∣ 01 ⟩ + 0 ∣ 10 ⟩ + 1 2 ∣ 11 ⟩ \frac{1}{\sqrt{2}}|00\rangle + 0|01\rangle + 0|10\rangle + \frac{1}{\sqrt{2}}|11\rangle 2 1∣00⟩+0∣01⟩+0∣10⟩+2 1∣11⟩

对应系数必须相等，于是我们得到一组方程组：

(1) a c = 1 2 ac = \frac{1}{\sqrt{2}} ac=2 1

(2) a d = 0 ad = 0 ad=0

(3) b c = 0 bc = 0 bc=0

(4) b d = 1 2 bd = \frac{1}{\sqrt{2}} bd=2 1

4.3 发现矛盾

• 根据方程(2)， a d = 0 ad = 0 ad=0，意味着要么 a = 0 a=0 a=0，要么 d = 0 d=0 d=0。
• 如果 a = 0 a = 0 a=0：那么代入方程 (1) 会得到 0 ⋅ c = 1 2 0 \cdot c = \frac{1}{\sqrt{2}} 0⋅c=2 1，这显然是不成立的（ 0 ≠ 0.707 0 \neq 0.707 0=0.707）。
• 如果 d = 0 d = 0 d=0：那么代入方程 (4) 会得到 b ⋅ 0 = 1 2 b \cdot 0 = \frac{1}{\sqrt{2}} b⋅0=2 1，这同样是不可能的。

4.4 结论

既然找不到任何一组系数 ( a , b , c , d ) (a, b, c, d) (a,b,c,d) 能满足这个方程组，说明 贝尔态 ∣ Φ + ⟩ |\Phi^+\rangle ∣Φ+⟩ 绝对不能写成两个独立量子态相乘的形式。

5 监听过程量子态演变

假设存在监听者 Eve，以下是监听过程量子态演变

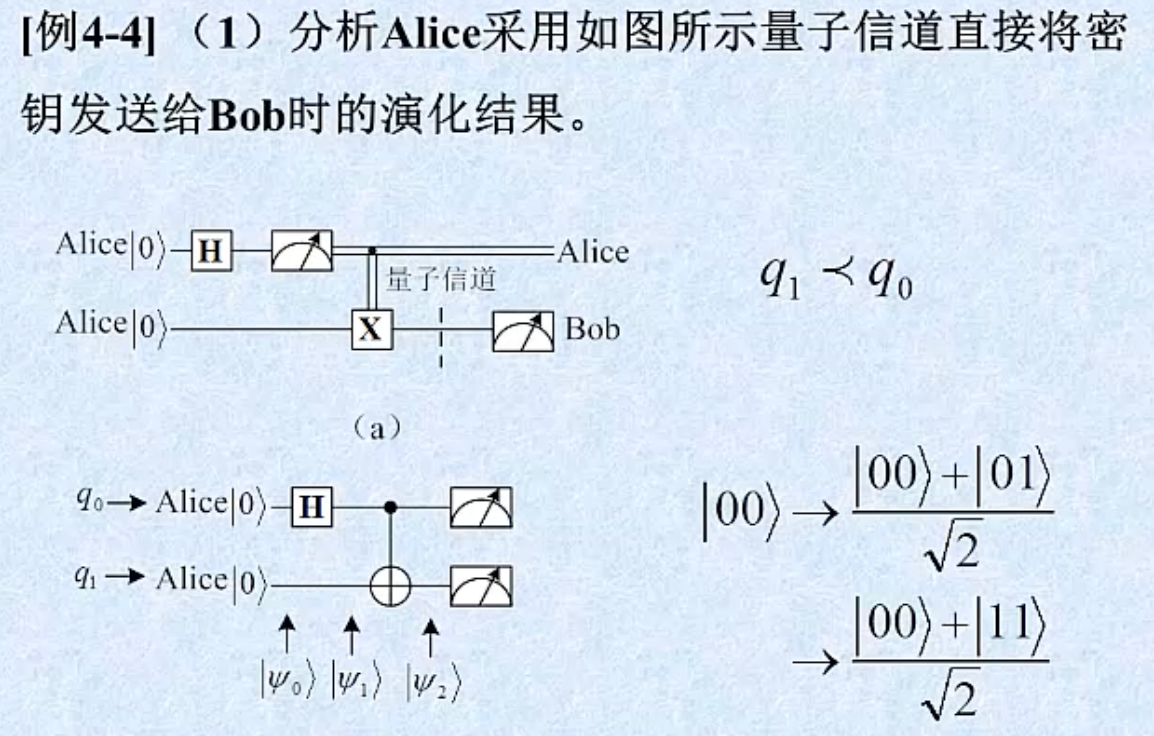
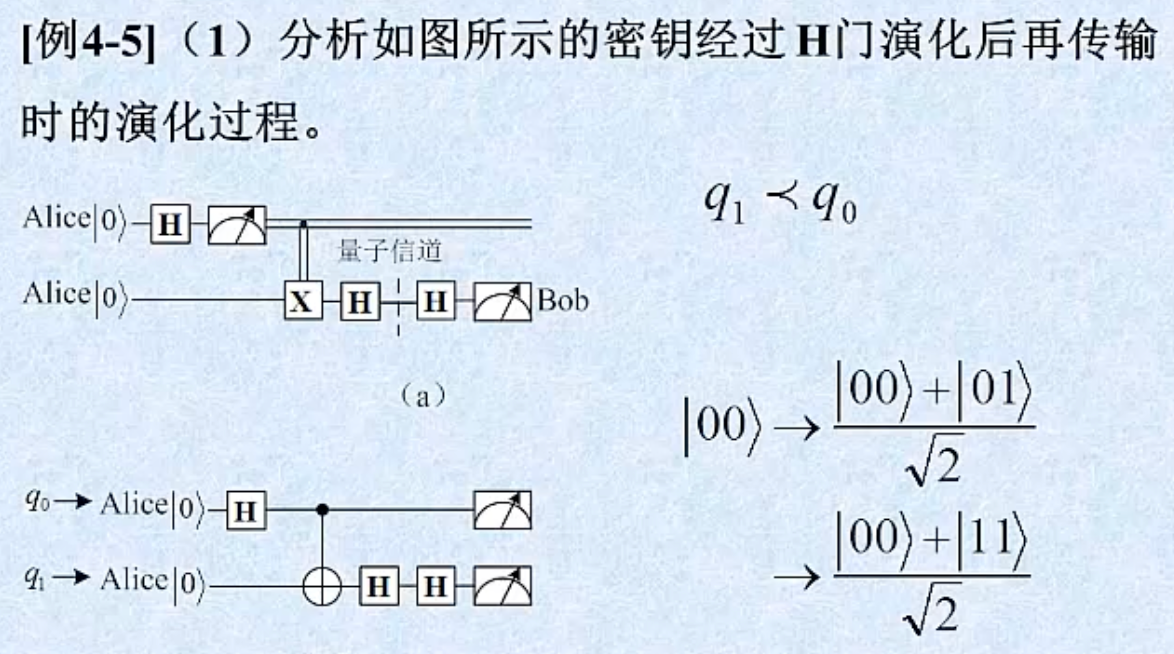
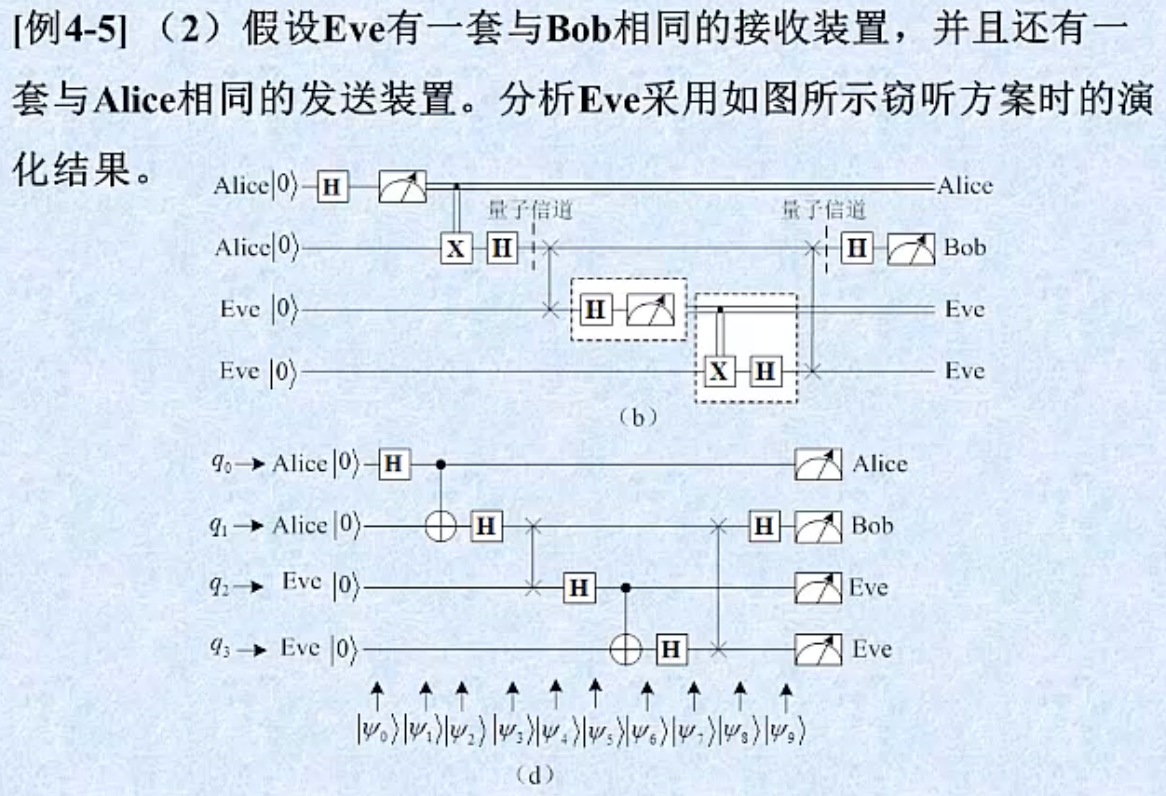
量子态序列分析

∣ ψ 0 ⟩ = ∣ 0000 ⟩ |\psi_0\rangle = |0000\rangle ∣ψ0⟩=∣0000⟩

∣ ψ 1 ⟩ = ∣ 0000 ⟩ + ∣ 0001 ⟩ 2 |\psi_1\rangle = \frac{|0000\rangle + |0001\rangle}{\sqrt{2}} ∣ψ1⟩=2 ∣0000⟩+∣0001⟩

∣ ψ 2 ⟩ = ∣ 0000 ⟩ + ∣ 0011 ⟩ 2 |\psi_2\rangle = \frac{|0000\rangle + |0011\rangle}{\sqrt{2}} ∣ψ2⟩=2 ∣0000⟩+∣0011⟩

∣ ψ 3 ⟩ = ∣ 0000 ⟩ + ∣ 0010 ⟩ + ∣ 0001 ⟩ − ∣ 0011 ⟩ 2 |\psi_3\rangle = \frac{|0000\rangle + |0010\rangle + |0001\rangle - |0011\rangle}{2} ∣ψ3⟩=2∣0000⟩+∣0010⟩+∣0001⟩−∣0011⟩

∣ ψ 4 ⟩ = ∣ 0000 ⟩ + ∣ 0100 ⟩ + ∣ 0001 ⟩ − ∣ 0101 ⟩ 2 |\psi_4\rangle = \frac{|0000\rangle + |0100\rangle + |0001\rangle - |0101\rangle}{2} ∣ψ4⟩=2∣0000⟩+∣0100⟩+∣0001⟩−∣0101⟩

∣ ψ 5 ⟩ = ∣ 0000 ⟩ + ∣ 0100 ⟩ + ∣ 0000 ⟩ − ∣ 0100 ⟩ + ∣ 0001 ⟩ + ∣ 0101 ⟩ − ∣ 0001 ⟩ + ∣ 0101 ⟩ 2 2 = ∣ 0000 ⟩ + ∣ 0101 ⟩ 2 \begin{aligned} |\psi_5\rangle &= \frac{|0000\rangle + |0100\rangle + |0000\rangle - |0100\rangle + |0001\rangle + |0101\rangle - |0001\rangle + |0101\rangle}{2\sqrt{2}} \\ &= \frac{|0000\rangle + |0101\rangle}{\sqrt{2}} \end{aligned} ∣ψ5⟩=22 ∣0000⟩+∣0100⟩+∣0000⟩−∣0100⟩+∣0001⟩+∣0101⟩−∣0001⟩+∣0101⟩=2 ∣0000⟩+∣0101⟩

∣ ψ 6 ⟩ = ∣ 0000 ⟩ + ∣ 1101 ⟩ 2 |\psi_6\rangle = \frac{|0000\rangle + |1101\rangle}{\sqrt{2}} ∣ψ6⟩=2 ∣0000⟩+∣1101⟩

∣ ψ 7 ⟩ = ∣ 0000 ⟩ + ∣ 1000 ⟩ + ∣ 0101 ⟩ − ∣ 1101 ⟩ 2 |\psi_7\rangle = \frac{|0000\rangle + |1000\rangle + |0101\rangle - |1101\rangle}{2} ∣ψ7⟩=2∣0000⟩+∣1000⟩+∣0101⟩−∣1101⟩

∣ ψ 8 ⟩ = ∣ 0000 ⟩ + ∣ 1000 ⟩ + ∣ 0101 ⟩ − ∣ 1101 ⟩ 2 |\psi_8\rangle = \frac{|0000\rangle + |1000\rangle + |0101\rangle - |1101\rangle}{2} ∣ψ8⟩=2∣0000⟩+∣1000⟩+∣0101⟩−∣1101⟩

∣ ψ 9 ⟩ = ∣ 0000 ⟩ + ∣ 0010 ⟩ + ∣ 0000 ⟩ − ∣ 0010 ⟩ + ∣ 0101 ⟩ + ∣ 0111 ⟩ − ∣ 0101 ⟩ + ∣ 0111 ⟩ 2 2 = ∣ 0 ⟩ ∣ 000 ⟩ + ∣ 111 ⟩ 2 \begin{aligned} |\psi_9\rangle &= \frac{|0000\rangle + |0010\rangle + |0000\rangle - |0010\rangle + |0101\rangle + |0111\rangle - |0101\rangle + |0111\rangle}{2\sqrt{2}} \\ &= |0\rangle \frac{|000\rangle + |111\rangle}{\sqrt{2}} \end{aligned} ∣ψ9⟩=22 ∣0000⟩+∣0010⟩+∣0000⟩−∣0010⟩+∣0101⟩+∣0111⟩−∣0101⟩+∣0111⟩=∣0⟩2 ∣000⟩+∣111⟩

参考文献

高岩《量子线路》