【读论文】纠缠双梳光谱学

目录

• 纠缠双梳光谱学
• • 一、引言
  • 二、纠缠双梳光谱学的原理
  • 三、纠缠增强型气体探测
  • 四、讨论
  • 致谢
  • 数据可用性
  • [附录A 实验细节](#附录A 实验细节)
  • • [A1 纠缠双梳光谱学装置](#A1 纠缠双梳光谱学装置)
    • [A2 纠缠梳的表征](#A2 纠缠梳的表征)
    • [A3 双梳光谱的采集](#A3 双梳光谱的采集)
  • [附录B 纠缠双梳光谱学的理论](#附录B 纠缠双梳光谱学的理论)
  • • [B1 输入和信道的建模](#B1 输入和信道的建模)
    • [B2 平衡外差光电流](#B2 平衡外差光电流)
    • [B3 平衡外差光电流均值的推导](#B3 平衡外差光电流均值的推导)
    • [B4 无先验知识的双次测量](#B4 无先验知识的双次测量)
    • [B5 有先验相位知识的单次测量](#B5 有先验相位知识的单次测量)
    • [B6 单侧吸收](#B6 单侧吸收)
    • [B7 平衡外差光电流中量子测量噪声的推导](#B7 平衡外差光电流中量子测量噪声的推导)
    • [B8 信噪比分析](#B8 信噪比分析)
    • [B9 双梳光谱学的经典极限](#B9 双梳光谱学的经典极限)
    • • [B9.1 纠缠双梳光谱学与外差接收器](#B9.1 纠缠双梳光谱学与外差接收器)
      • [B9.2 压缩双梳光谱学与分束接收器](#B9.2 压缩双梳光谱学与分束接收器)
  • 参考文献

纠缠双梳光谱学

《物理评论X》 2025年第15卷，041009期

《物理学》重点刊载

阿卜杜勒卡里姆·哈里里¹、刘帅¹、石昊²、庄群涛²,³*、范旭东⁴、张哲深

1 美国密歇根州安阿伯市密歇根大学电气工程与计算机科学系，48109

2 美国加利福尼亚州洛杉矶市南加州大学明谢电气工程与计算机科学系，90089

3 美国加利福尼亚州洛杉矶市南加州大学物理与天文学系，90089

4 美国密歇根州安阿伯市密歇根大学生物医学工程系，48109

（2025年3月13日收稿；2025年6月28日修回；2025年8月28日录用；2025年10月15日发表）

光学频率梳已成为光谱学、测距、光学钟、时间与频率传递、波形合成和通信等众多领域的核心技术。然而，光载波的量子力学涨落对经典光学频率梳的测量精度构成了根本性限制，在干涉测量和光谱学应用中尤为显著。纠缠作为一种典型的量子资源，能够突破经典系统的根本极限。本文将纠缠引入光学频率梳领域，提出了纠缠双梳光谱学（EDCS），该技术突破了经典双梳光谱学（DCS）的固有极限。纠缠双梳光谱学利用频率梳上定制的纠缠结构，实现了所有梳齿的同时探测，且探测精度低于经典双梳光谱学的标准量子极限。将该技术应用于气体探测时，相较于经典双梳光谱学，我们实现了2.6分贝的信噪比提升和1.7倍的积分时间缩短，这使得纠缠双梳光谱学特别适用于对功率受限、需要快速高精度测量的动态化学和生物传感领域。该技术为量子频率梳的应用开辟了新途径，凸显了其在精密计量、光谱学和守时等诸多领域的应用前景。

数字对象标识符 ：10.1103/plh2-cr8s
研究领域：量子信息

一、引言

纠缠是一种无经典对应物的量子力学特性，表现为两个或多个客体间存在强于经典关联的量子关联。自首次被发现以来1-3，纠缠已从一个科学争论的主题，发展成为一种能实现经典物理极限之外功能的变革性资源4。如今，纠缠已成为量子计算5、量子通信6,7、量子传感8-11和量子成像12等众多量子协议的核心，为突破量子力学涨落带来的根本极限提供了途径4。在这方面，量子协议的一个关键性能指标是，在经典和量子体系受相同资源约束的条件下，其在信噪比、测量灵敏度或积分时间等方面相较于最优经典方案的优势。

光学频率梳是一种变革性工具，由一系列等间距、相位相干的激光谱线组成，在光谱学13,14、测距15、光学钟16和波形合成17等应用中展现出优异性能。在此背景下，双梳光谱学应运而生，成为一种强大的技术，因其在短测量时间内可实现超高灵敏度和宽带宽的探测能力而闻名。尽管如此，双梳光谱学作为一种经典方法，仍受限于量子噪声带来的灵敏度与测量时间之间的根本性权衡。近年来，已有研究证明双梳光谱学的性能可达到量子噪声极限18-20，由此引出一个关键问题：如何像引力波探测21、分布式量子传感22,23和量子照明24领域那样，在双梳光谱学结构中利用量子资源，以突破这一根本极限？

近期，量子增强光谱学协议25,26相继被提出，旨在突破基于经典频率梳的光谱学根本极限。具体而言，文献25提出了一种利用宽带压缩光、电光调制和零差探测来构建量子频率梳的方案，该量子频率梳可突破经典光谱学的散粒噪声极限。然而，由于缺乏双梳结构，该方案的光学测量实际带宽无法达到与双梳光谱学相当的宽光谱覆盖范围。与此同时，文献26设计了一种基于量子梳的双梳光谱学协议，该量子梳由经本地振荡器梳齿外差探测的单个压缩谱线组成。但理想量子梳的产生难度极大，因其需要非线性光学过程满足相位匹配带宽窄于梳齿间距，且群速度匹配带宽与频率梳的带宽相当26。因此，尽管这些方案在理论上前景良好，但在实验上实现量子频率梳光谱学的计量优势仍是一项亟待解决的挑战。

在实验方面，近期有研究报道了压缩双梳光谱学27，相较于对比的非最优经典双梳光谱学协议，实现了3分贝的信噪比提升。这项工作标志着将非经典资源融入双梳架构的重要一步，但由于未在量子和经典体系受相同功率约束的条件下与最优经典结构进行对比，其并未确立计量学上的量子优势28。在本文2.1节和附录B中，我们通过正式的理论分析，确定了经典和量子资源下双梳光谱学的最优性能极限。此类基准测试对于证实量子计量协议的量子优势声明至关重要。

本文提出并实验验证了纠缠双梳光谱学，该技术突破了经典双梳光谱学的根本极限。与基于克尔非线性光纤系统产生的振幅孤子压缩的压缩双梳光谱学27不同，纠缠双梳光谱学利用的是一种明亮量子梳，该量子梳通过将自发参量下转换产生的一系列双模压缩态与经典梳齿相干位移得到，其梳齿间存在非经典关联。单模压缩仅能实现一个正交分量低于散粒噪声水平的测量，而双模压缩态中蕴含的纠缠则为振幅和相位正交分量的亚散粒噪声探测开辟了道路，这一点在量子密集计量中已得到验证29。通过利用自发参量下转换过程中同时产生的大量光学模间的纠缠光谱结构，纠缠双梳光谱学实现了所有梳齿的同时探测，且探测精度低于标准量子极限。实验结果表明，相较于经典双梳光谱学，该技术实现了2.6分贝的信噪比提升和1.7倍的积分时间缩短。我们的实验为将量子资源融入双梳光谱学搭建了稳健的框架，为高精度传感和计量领域的变革性发展铺平了道路。

二、纠缠双梳光谱学的原理

我们的纠缠双梳光谱学方案需要使用三个频率梳源：一是纠缠梳，用于提供实现亚标准量子极限性能所需的量子关联；二是经典梳，通过与纠缠梳相干位移产生明亮的纠缠信号梳，并将其传输至样品；三是经典本地振荡器梳，用于同时测量所有纠缠信号梳的梳齿。图1所示的纠缠双梳光谱学实验原理图展示了三个梳源之间的相互作用。实验以1550纳米连续波光纤激光器为种子源，将其注入光学参量振荡器腔，以产生纠缠梳30，在相互作用绘景中，其哈密顿量可表示为：
H ^ = i ℏ χ ∑ n = 0 N ( a ^ S − n † a ^ S n † − a ^ S − n a ^ S n ) \hat{H}=i \hbar \chi \sum_{n=0}^{N}\left(\hat{a}{S{-n}}^{\dagger} \hat{a}{S{n}}^{\dagger}-\hat{a}{S{-n}} \hat{a}{S{n}}\right) H^=iℏχn=0∑N(a^S−n†a^Sn†−a^S−na^Sn)

其中， a ^ S n \hat{a}{S{n}} a^Sn和 a ^ S n † \hat{a}{S{n}}^{\dagger} a^Sn†分别为纠缠梳第 n n n个模式的湮灭算符和产生算符， ℏ \hbar ℏ为约化普朗克常数， χ \chi χ为非线性相互作用强度。式中， a ^ S − n † a ^ S n † \hat{a}{S{-n}}^{\dagger} \hat{a}{S{n}}^{\dagger} a^S−n†a^Sn†（ a ^ S − n a ^ S n \hat{a}{S{-n}} \hat{a}{S{n}} a^S−na^Sn）描述了通过自发参量下转换在第 n n n和 − n -n −n个模式中产生（湮灭）一对光子的过程。所有模式对均通过并行的自发参量下转换过程，形成具有特定光谱结构的纠缠梳：其中央梳齿为位移单模压缩态，其余梳齿则形成双模压缩真空态对，如图2所示。梳齿间距必须为光学参量振荡器腔自由光谱范围的整数倍，本实验中将其设置为17.565吉赫，以适配用于调控经典梳和本地振荡器梳的可编程光学滤波器的分辨率。纠缠梳的总梳齿数 N N N由自发参量下转换的相位匹配带宽与光学参量振荡器腔自由光谱范围的比值决定。在量子源处，仅中央梳齿的光功率为数十微瓦，其余梳齿均处于双模压缩真空态。为产生用于探测样品的明亮纠缠信号梳，将纠缠梳与光谱匹配的经典梳在非平衡分束器上发生干涉，将每个双模压缩真空态对转换为位移双模压缩态，每个梳齿的光功率可达数百微瓦。纠缠信号梳穿过样品后，采用外差探测结构对其进行测量，使其与本地振荡器梳发生拍频。本地振荡器梳和信号梳均由同一连续波激光器产生，二者分别经过电光调制和可编程光学滤波器的光谱整形，以调控每个梳齿的光强和相位。

在实验中，本地振荡器梳的电光调制频率决定了双梳光谱学系统的重复频率 f r e p f_{rep} frep，并将其设置为17.565吉赫，与纠缠梳的梳齿间距匹配。经典梳的调制频率与 f r e p f_{rep} frep存在4兆赫的偏移量 δ f r e p \delta f_{rep} δfrep。通过该设置，外差探测中本地振荡器梳与纠缠信号梳的拍频会产生线间距为 δ f r e p \delta f_{rep} δfrep的射频梳，随后由电子设备对其进行采集和处理。纠缠信号梳的可用带宽为0.17569太赫，该带宽受限于本地振荡器梳和经典梳在高模式数下的功率滚降（更多实验细节见本文第四节和附录A）。我们将纠缠双梳光谱学协议的性能与标准量子极限进行对比，该标准量子极限由经典量子噪声极限双梳光谱学协议确定，该协议采用相同的经典梳和本地振荡器梳结构，且关闭纠缠梳。

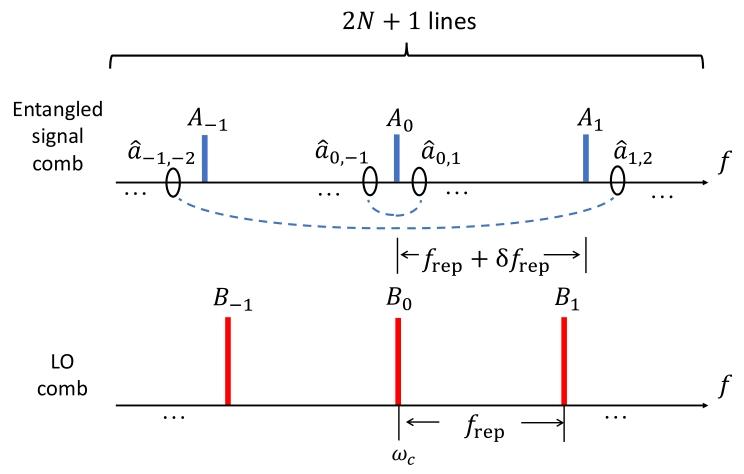
图2展示了纠缠信号梳中蕴含的纠缠结构及其光谱配置，同时给出了本地振荡器梳的光谱配置。光学参量振荡器腔在中心频率处产生单模压缩态，同时产生由双模压缩真空态对组成的纠缠梳，双模压缩真空态对由相互连接的虚线和量子算符 a ^ S n \hat{a}{S{n}} a^Sn、 a ^ S − n \hat{a}{S{-n}} a^S−n表示，其频率与中心腔共振频率的差值为 f r e p f_{rep} frep的整数倍，其中 f r e p f_{rep} frep由光学参量振荡器腔的自由光谱范围决定。图中以洛伦兹线型描绘了光学参量振荡器腔的线宽 Δ ν \Delta \nu Δν。经典梳的梳齿间距与纠缠梳相差 δ f r e p \delta f_{rep} δfrep，因此二者在图1中的分束器BS₁处发生的干涉，会在频率 n ( f r e p + δ f r e p ) n(f_{rep}+\delta f_{rep}) n(frep+δfrep)处产生位移 α S n \alpha_{S_{n}} αSn，如图中红线所示。本地振荡器梳的梳齿间距与纠缠梳在 f r e p f_{rep} frep处匹配，借助双模压缩真空态中蕴含的纠缠特性，可实现所有纠缠信号梳齿的同时探测，且探测精度低于标准量子极限。同时，频率为 n f r e p n f_{rep} nfrep的本地振荡器梳齿与频率为 n ( f r e p + δ f r e p ) n(f_{rep}+\delta f_{rep}) n(frep+δfrep)的纠缠信号梳位移之间的拍频，会在射频光谱中产生频率为 n δ f r e p n \delta f_{rep} nδfrep的拍频信号。通过对每个梳齿的位移进行合理设计，可分辨出纠缠信号梳和本地振荡器梳第 n n n个梳齿拍频产生的混叠现象（见本文第四节）。图3(a)展示了纠缠信号梳或经典信号梳与本地振荡器梳拍频得到的射频光谱，证明了纠缠梳结构带来的2.6分贝信噪比提升。为解决高拍频信号处相位噪声增大的问题，我们有意降低了经典信号梳的功率。该调整实现了散粒噪声极限测量带宽的拓展，如图3(b)和3(c)所示。

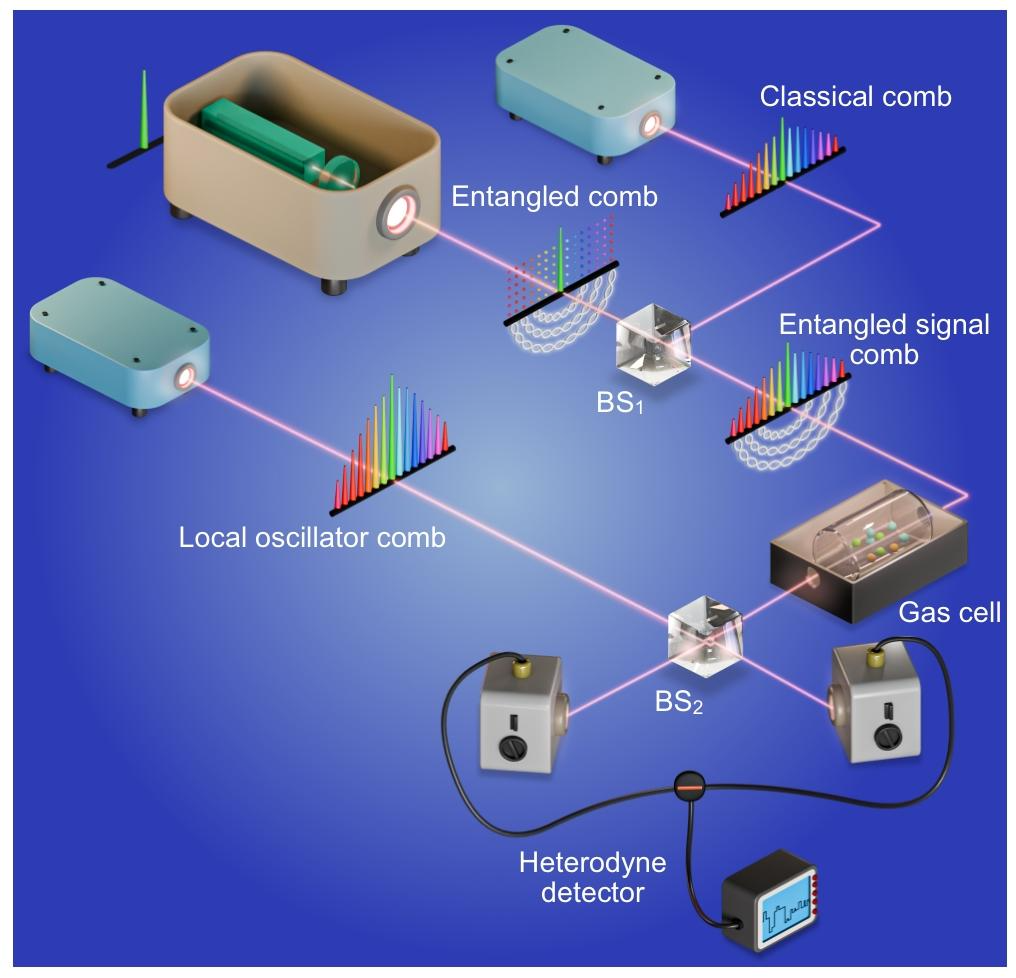
【图1 纠缠双梳光谱学的实验装置】

纠缠光学频率梳与经典梳在分束器BS₁处相干位移，产生明亮的纠缠信号梳。该信号梳穿过气体样品，用于光谱分析。通过与本地振荡器梳进行干涉测量，采用外差探测结构提取气体的吸收特征。该协议利用纠缠梳的亚标准量子极限探测能力，实现了相较于经典双梳光谱学更高的灵敏度和更短的积分时间。双螺旋图案：梳齿间的纠缠；虚线：双模压缩真空态。

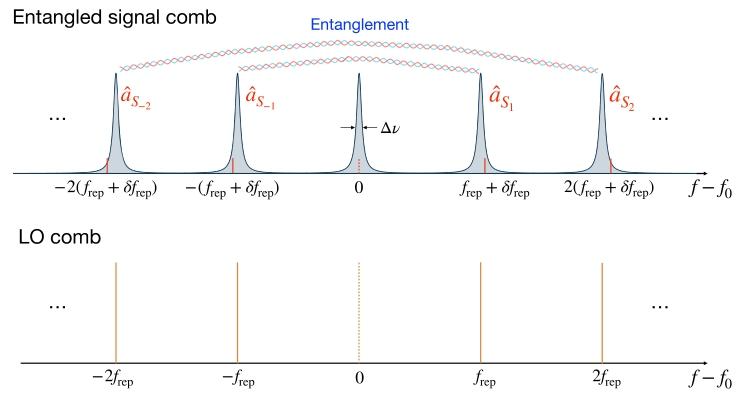
【图2 纠缠信号梳和本地振荡器梳的纠缠结构及光谱配置】

光学参量振荡器腔产生的 a ^ S n \hat{a}{S{n}} a^Sn和 a ^ S − n \hat{a}{S{-n}} a^S−n形成双模压缩真空态对，构成纠缠梳。本地振荡器梳的梳齿间距与纠缠梳在 f r e p f_{rep} frep处锁定，可实现所有纠缠信号梳齿的同时探测，且探测精度低于标准量子极限。经典梳在频率 n ( f r e p + δ f r e p ) n(f_{rep}+\delta f_{rep}) n(frep+δfrep)处通过位移 α S n \alpha_{S_{n}} αSn对纠缠梳进行调制，产生明亮的纠缠信号梳。中央虚线梳齿仅用于相位锁定， f 0 f_0 f0为频率梳的中心频率。

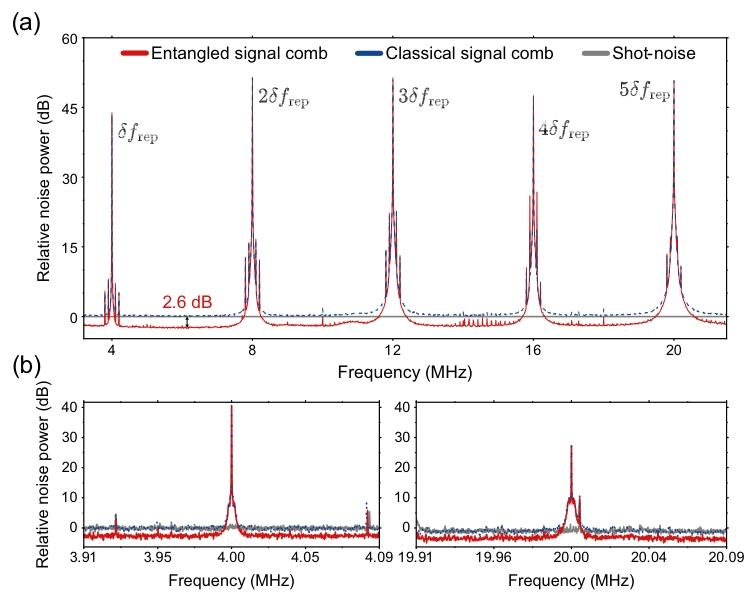
【 图3 纠缠双梳和经典双梳的射频光谱】

(a) 纠缠信号梳、经典信号梳分别与本地振荡器梳拍频得到的射频光谱；(b) 降低经典信号梳功率后，第一阶（左）和第五阶（右）拍频信号的放大射频光谱，低功率工作模式可抑制记录拍频信号中的相位噪声。

经典和量子双梳光谱学的性能基准

附录B对经典双梳光谱学和纠缠双梳光谱学进行了全面的性能基准测试。本文针对弱吸收区的均匀梳和压缩光谱，推导了信噪比基准公式，直观展示纠缠双梳光谱学相较于经典双梳光谱学的优势。后续章节将采用通用理论，在分析实验数据和与经典双梳光谱学协议对比时，不再依赖上述假设。对于均匀梳，将纠缠信号梳和本地振荡器梳的梳齿振幅 { A n } \{A_n\} {An}、 { B n } \{B_n\} {Bn}，以及附录B中定义的压缩增益 { G n } \{G_n\} {Gn}均设置为均匀值，即 A n = A A_n=A An=A、 B n = B B_n=B Bn=B、 G n = G G_n=G Gn=G；同时，吸收光谱的功率透射率 { κ n } \{\kappa_n\} {κn}趋近于1，即 κ n → 1 \kappa_n \to 1 κn→1，其中 n n n为梳齿编号。此外，假设本地振荡器梳的光强远大于信号梳，即 ∣ B ∣ ≫ ∣ A ∣ |B| \gg |A| ∣B∣≫∣A∣，且本地振荡器梳不与样品发生相互作用。

作为量子计量的标准做法，我们首先将功率约束定义为不同协议间公平对比的关键参数。在非对称纠缠双梳光谱学系统中，仅有一束梳与样品相互作用，该功率约束由样品接收的总功率 P = ℏ ω c A 2 M / T P=\hbar \omega_c A^2 M/T P=ℏωcA2M/T决定，其中 M M M为总梳齿数。

在强本地振荡器极限下，由公式(B17)可推导出外差探测的信噪比为：
( S N R m ∣ κ n → 1 ) 2 = A 2 B 2 M ( B 2 / 2 G + A 2 / 2 ) ≈ A 2 M / 2 G (2) \left(\left.SNR_{m}\right|{\kappa{n} \to 1}\right)^{2}=\frac{A^{2} B^{2}}{M\left(B^{2} / 2 G+A^{2} / 2\right)} \approx \frac{A^{2}}{M / 2 G} \tag{2} (SNRm∣κn→1)2=M(B2/2G+A2/2)A2B2≈M/2GA2(2)

从物理意义上看，分母为 M / 2 M/2 M/2个双模压缩模式对与对应本地振荡器模式拍频产生的总噪声方差。每个本地振荡器模式的振幅为 B B B，因此外差探测中一对本地振荡器模式的散粒噪声方差为 B 2 B^2 B2，而双模压缩可将该方差降低至 B 2 / G B^2/G B2/G。因此， M / 2 M/2 M/2个模式对产生的总噪声方差为 M B 2 / 2 G M B^2/2G MB2/2G。

令 G = 1 G=1 G=1，可得经典极限下的信噪比为：
( S N R C L a s y m ) 2 = A 2 M / 2 = 2 P T M 2 ℏ ω c (3) \left(SNR_{CL}^{asym }\right)^{2}=\frac{A^{2}}{M / 2}=\frac{2 P T}{M^{2} \hbar \omega_{c}} \tag{3} (SNRCLasym)2=M/2A2=M2ℏωc2PT(3)

通过类似的推导方法，可得到对称纠缠双梳光谱学的信噪比14。在对称结构中，两束梳在50:50分束器上合束后穿过样品，其信噪比为：
( S N R C s y m ) 2 = A 2 B 2 M ( A 2 + B 2 ) / 2 (4) \left(SNR_{C}^{sym}\right)^{2}=\frac{A^{2} B^{2}}{M\left(A^{2}+B^{2}\right) / 2} \tag{4} (SNRCsym)2=M(A2+B2)/2A2B2(4)

与非对称双梳光谱学类似，将样品接收的总光功率 P P P作为约束条件，令两束梳的功率相等，即 A 2 = B 2 = P T / ( M ℏ ω c ) A^2=B^2=PT/(M\hbar\omega_c) A2=B2=PT/(Mℏωc)，可得对称双梳光谱学经典极限下的信噪比：
( S N R C L s y m ) 2 = P T M 2 ℏ ω c (5) \left(SNR_{CL}^{sym}\right)^{2}=\frac{P T}{M^{2} \hbar \omega_{c}} \tag{5} (SNRCLsym)2=M2ℏωcPT(5)

该结果与文献14中提出的双梳光谱学散粒噪声极限信噪比一致。在文献27的压缩双梳光谱学实验中，一束梳的光强比另一束高3个数量级，导致其信噪比相较于公式(5)中两束等功率梳实现的经典极限低2个数量级以上。在文献27实验的这种非平衡结构中，测量噪声主要由强光强梳的散粒噪声主导，因此对该梳进行压缩，可相较于采用相同非平衡功率的经典双梳光谱学方案实现信噪比提升。有人可能会提出疑问：若压缩梳与经典梳的功率平衡，这种量子优势是否仍然存在？遗憾的是，功率平衡后，经典梳与压缩梳拍频时会拾取压缩梳反压缩正交分量的噪声，文献27的作者近期也验证了这一点32，这使得该方案在功率约束下无法超越最优经典双梳光谱学的性能。因此，要在双梳光谱学中实现量子优势，需要对两束梳的量子态进行精细的设计和调控，这一点在本实验中得以实现。

三、纠缠增强型气体探测

我们采用非对称方案验证了纠缠双梳光谱学在气体探测中的应用，该方案中仅有纠缠信号梳入射至目标样品，在通过强光强本地振荡器梳和平衡探测实现高效技术噪声抑制的同时，最大限度降低了样品损伤的风险。图4(a)展示了本地振荡器梳的光学光谱，其梳齿间距 f r e p = 17.565 f_{rep}=17.565 frep=17.565吉赫，该参数的选择既与产生纠缠频率梳的光学参量振荡器腔自由光谱范围匹配，又适配可编程光学滤波器的分辨率。为实现更高的光谱分辨率，我们将连续波种子激光器的中心频率调整至50个不同的位置，并在每个位置采集双梳光谱。将这些梳齿间距为17.565吉赫的光谱进行离线交织，合成出有效分辨率约为350兆赫的宽带光谱，该分辨率由50次采集的设计扫描步长决定，如图4(b)-(d)所示。由于载波偏置频率为零，光谱的中心区域无梳齿，因此无法观测到拍频信号。实验中，三束梳的中央梳齿均用于锁定纠缠梳的位移，并将本地振荡器梳锁定至压缩正交分量。这两个锁定单元对于维持纠缠双梳光谱学测量的稳定性至关重要。

在气体探测实验中，频率偏移 δ f r e p = 4 \delta f_{rep}=4 δfrep=4兆赫的纠缠信号梳穿过含有氰化氢（HCN）的气体池，气体池的压强为25托，光程长度为17.5厘米，对应的吸收深度为3分贝。我们采用与图4(b)相同的梳结构和连续波激光器扫描方式，获取氰化氢的吸收光谱。图5(a)展示了测量得到的平均透射光谱，并基于HITRAN2020数据库33，以光程长度、压强、温度和浓度为输入参数，采用模型对光谱进行拟合，实验数据与拟合模型具有良好的一致性。为验证纠缠双梳光谱学实现的测量加速效果，我们将透射光谱测量的精度作为平均干涉图数量的函数进行估算。利用平衡光电探测器探测干涉图，并通过具有足够带宽的示波器以100兆采样/秒的速率进行记录。滤波后，提取10微秒的时域信号段，对应分辨率带宽为100千赫的单个干涉图。图5(b)展示了测量精度随平均干涉图数量的变化关系，结果表明，在达到目标测量精度时，纠缠双梳光谱学相较于经典双梳光谱学实现了1.7倍的量子加速。这一进展凸显了纠缠双梳光谱学突破灵敏度与测量时间之间根本性权衡的潜力，为实现更高速度、更高精度的传感应用铺平了道路。

我们进一步评估了纠缠双梳光谱学在不同吸收深度下的性能，结果如图6所示。图6(a)展示了纠缠双梳光谱学和经典双梳光谱学的单梳齿信噪比（ S N R m SNR_m SNRm，其正式定义为估算第 m m m个梳齿光谱 κ m \kappa_m κm的功率信噪比，见附录B）；图6(b)展示了不同吸收深度下，所有梳齿同时探测的信噪比优势。值得注意的是，与0.1分贝和0.25分贝的低吸收深度相比，即使在3分贝的吸收深度下，该量子优势仍基本保持。这种鲁棒性源于本实验结构中经典和量子资源的协同作用：纠缠双梳光谱学利用双模压缩真空态的非经典特性实现亚标准量子极限性能，同时其分布式结构最大限度降低了损耗对量子优势的影响，因为在光谱测量中，仅有小部分梳齿会受到损耗影响。关键在于，本实验装置中梳齿的未衰减-衰减比（UAR）达到10:1，这使得亚标准量子极限性能的衰减程度降至最低。为进一步验证纠缠双梳光谱学的性能，我们模拟了具有10分贝最大压缩和15分贝最大反压缩的平顶纠缠梳在平顶本地振荡器探测下的性能，结果如图6©所示，证明了纠缠梳对损耗的强耐受性，这一特性源于其梳齿的高未衰减-衰减比。

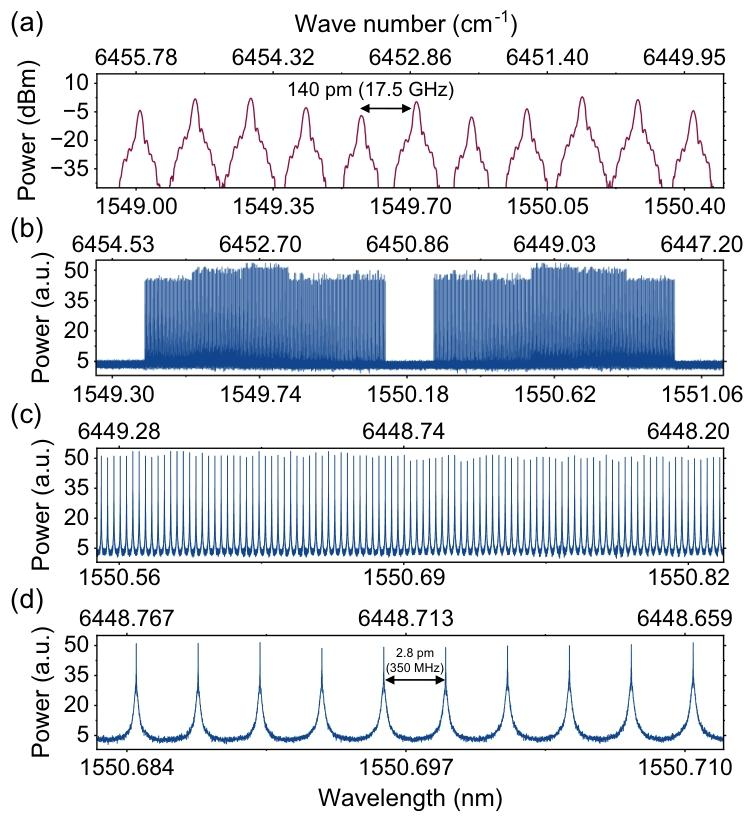
【图4 测量得到的本地振荡器梳和双梳光谱】

(a) 利用光学光谱仪测量的本地振荡器梳光谱；(b) 以100兆赫的采样率对平衡接收器的光电流差值时域信号采样0.5秒，得到双梳光谱，对数据进行后处理以推导频域光谱，通过扫描连续波激光器的中心频率实现更多梳齿的探测；© 35吉赫带宽的放大视图，凸显双梳光谱的模式分辨特性；(d) 进一步放大至3.5吉赫带宽，可分辨出单个梳齿。

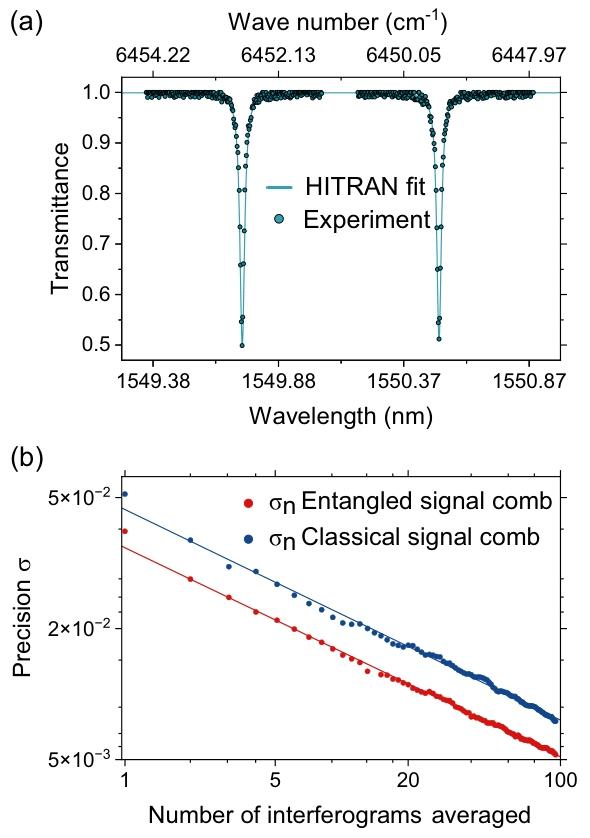
【 图5 测量得到的吸收光谱及量子加速效果】

(a) 利用纠缠双梳光谱学获取的吸收光谱，并基于HITRAN数据库进行拟合，证明了测量的准确性。拟合值与实验值差值的标准偏差为1.1%，在吸收峰值附近观测到的最大差值小于7%；(b) 纠缠双梳光谱学相较于经典双梳光谱学的量子加速效果，该效果由亚标准量子极限带来的测量精度提升实现。

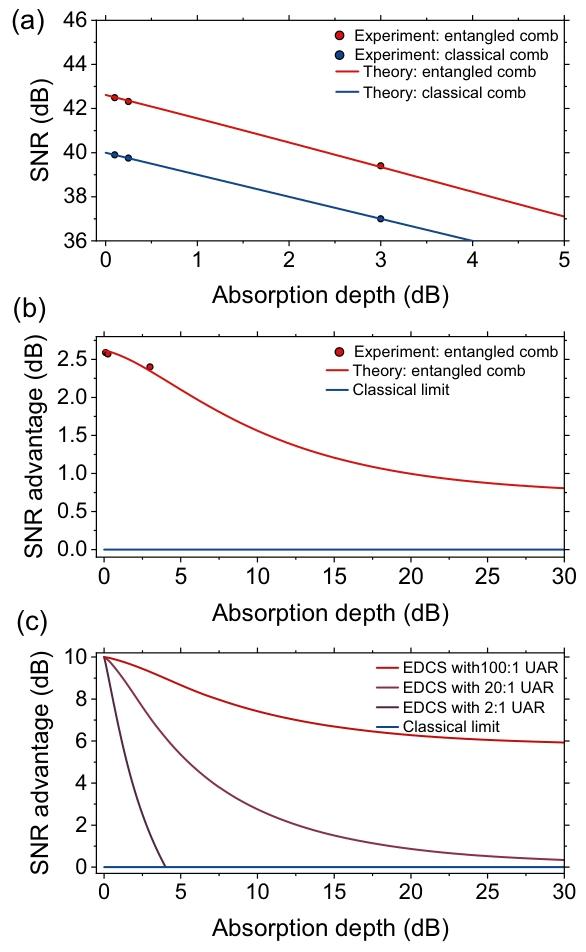
【 图6 纠缠双梳光谱学的量子优势对样品吸收的鲁棒性】

(a) 纠缠双梳光谱学和经典双梳光谱学的信噪比随气体池吸收深度的变化关系，尽管中等吸收深度下衰减增强，但纠缠双梳光谱学相较于经典双梳光谱学的量子优势仍十分显著，每个实验数据点的标准偏差为0.6分贝；(b) 纠缠双梳光谱学相较于经典双梳光谱学的信噪比优势，表明量子优势随吸收深度的增加缓慢衰减并最终趋于饱和，每个实验数据点的标准偏差为0.08分贝；© 具有10分贝最大压缩和15分贝最大反压缩的平顶纠缠梳在平顶本地振荡器探测下的模拟性能，证明了维持目标量子优势水平所需的梳齿未衰减-衰减比。

四、讨论

我们利用纠缠光谱结构实现了线性吸收双梳光谱学，实现了信噪比提升、测量灵敏度提高和积分时间缩短。本实验装置新增了一个伺服环路，用于锁定纠缠梳与经典信号梳之间的相对相位，其余反馈环路均与传统双模压缩真空源的环路一致。为满足更高的相位要求并克服纠缠双梳光谱学中的锁定难题，本实验主要依赖两项关键技术：（1）电光梳产生：单个连续波激光器为光学腔提供种子光，并通过电光调制同时产生经典信号梳和本地振荡器梳。该公共种子源保证了二者的固有相干性34，实现了纠缠信号梳的亚散粒噪声探测、经典梳的散粒噪声极限探测，以及与本地振荡器梳的稳健相位锁定；（2）可编程光学滤波：利用波整形器精确调控经典信号梳和本地振荡器梳每个梳齿的振幅和相位。尽管纠缠梳不经过滤波器，但其有效正交分量方向和功率分布可通过经典梳的相干位移进行间接调控。这种调控对于相位敏感外差探测至关重要：电光调制在本地振荡器梳中引入的非均匀光谱相位必须得到校正，以实现所有压缩正交分量的对准；此外，经典梳的光谱相位分布必须与本地振荡器梳匹配，以最大化拍频信号强度。相位失准会导致压缩和反压缩正交分量混合，从而增大噪声功率，或因信号梳与本地振荡器梳之间的相位失准导致信号功率降低，最终使量子增强效果减弱。可编程滤波器还能实现各模式间的光功率均衡，并通过必要的梳齿衰减抑制射频光谱中的额外相位噪声。为证实观测到的2.6分贝量子优势是真实存在的，而非滤波器设置带来的假象，我们在保持波整形器配置不变的情况下，通过开启和关闭量子梳来采集双梳光谱，结果显示量子优势保持不变，验证了我们提出的纠缠双梳光谱学方案的稳健性。

在当前的纠缠和光谱配置下，纠缠信号梳与本地振荡器梳第 n n n和 − n -n −n个梳齿之间的拍频，均会转换为射频频率 n δ f r e p n \delta f_{rep} nδfrep处的相同信号。我们提出了两种方法来解决该混叠问题（见附录B）：第一种方法采用双次测量方案，在两次连续测量中，分别将正指数纠缠梳齿的位移设置为 α S n \alpha_{S_n} αSn和 − α S n -\alpha_{S_n} −αSn。由于两次测量中射频频率 n δ f r e p n \delta f_{rep} nδfrep处的拍频信号分别为 α S − n + α S n \alpha_{S_{-n}}+\alpha_{S_n} αS−n+αSn和 α S − n − α S n \alpha_{S_{-n}}-\alpha_{S_n} αS−n−αSn，因此对两次测量结果进行求和和求差，可分别得到 2 α S − n 2\alpha_{S_{-n}} 2αS−n和 2 α S n 2\alpha_{S_n} 2αSn，且不会降低整体信噪比；第二种方法将正、负指数梳齿沿两个不同的正交分量进行位移，数学上分别表示为实位移和虚位移。此时，纠缠信号梳与本地振荡器梳第 n n n和 − n -n −n个梳齿的拍频会产生与 c o s ( 2 π n δ f r e p t ) cos(2\pi n \delta f_{rep}t) cos(2πnδfrept)和 s i n ( 2 π n δ f r e p t ) sin(2\pi n \delta f_{rep}t) sin(2πnδfrept)成正比的射频信号，通过两个射频混频器可明确区分正、负指数梳齿。

值得注意的是，本文所验证的纠缠双梳光谱学协议与文献26提出的协议在量子梳结构和测量方案上均存在差异。具体而言，文献26采用的是一系列单模压缩态，其梳齿间无交叉关联；而本实验使用的量子梳具有成对纠缠的梳齿（双模压缩）。纠缠模式正交分量间的量子关联（而非偏振间的关联）赋予了纠缠双梳光谱学增强效果。该方法可利用标准双模压缩真空源，同时为集成到与χ⁽³⁾兼容的互补金属氧化物半导体硅光子学平台奠定了基础。这些平台在量子光产生方面取得了重大进展35-40，已接近实现体量子源的最高压缩测量水平41。此外，这些平台有望调控色散分布42,43，以产生超宽带量子梳，并将经典克尔频率梳与可编程光学滤波器44集成作为本地振荡器梳，为开发具有高度紧凑性和多功能性、且性能优于经典方案的纠缠双梳光谱学平台开辟了新途径45。

如文献18,46,47所述，利用电光调制器实现的双梳光谱学存在光谱范围有限的问题（本实验中还表现为梳齿数较少），而这一问题可通过连续波激光器和射频合成器的频率可调性有效解决。这种灵活性允许对梳的中心频率和重复频率进行精确调控，使实验配置具有高度的灵活性。尽管存在这些限制，该方法仍能在短测量时间内实现高信噪比，并支持定制化的光谱分辨率。在当前配置下，我们的纠缠双梳光谱学装置的光谱分辨率为350兆赫，如图4(d)所示。为填补这些间隔中的剩余空白，可在每个激光器中心频率处将射频扫描175兆赫。该两步法可保证完整的光谱覆盖，同时保持量子优势，因为在激光器和射频扫描过程中，所有梳齿均处于纠缠梳源400兆赫的压缩带宽范围内。关于进一步拓展光谱覆盖范围，已有多种技术被提出并验证：例如，高效非线性展宽技术可实现高分辨率的更宽带宽探测48；此外，级联电光调制器也是显著增加光谱覆盖范围的有效方法49。

纠缠双梳光谱学相较于经典双梳光谱学的优势可通过多种途径进一步扩大：首先，本实验中纠缠梳源产生的真空压缩最大约为4分贝，而已有研究报道了超过10分贝的压缩源41；其次，本实验使用的射频合成器在10吉赫频率、10千赫偏置下的相位噪声水平为-75分贝每赫兹，而商用标准射频合成器在该条件下的相位噪声可达-132分贝每赫兹，这将进一步扩大纠缠双梳光谱学与经典双梳光谱学在积分时间上的差距；第三，降低实验缺陷的影响，如波整形器相位滤波配置的误差、纠缠信号梳与本地振荡器梳模式失配导致的条纹可见度低于1（本实验为97%），以及光电二极管的量子效率有限（本实验为88%），这些措施将减少压缩和反压缩正交分量的混合，以及混入的真空噪声，使纠缠双梳光谱学的量子优势更加显著。

我们注意到，通过对公式(B17)的分析（见附录B），可进一步优化图6©中的理论结果，这揭示了从双梳光谱学向纠缠双梳光谱学转变时的额外自由度和关键考虑因素。第一种优化方法是在不降低压缩程度的前提下，通过降低光学参量振荡器腔的泵浦功率来最小化反压缩，这将减少图6©中观测到的反压缩对量子优势衰减的影响；第二种方法采用自适应测量，对本地振荡器进行配置，以模拟信号梳因吸收损耗产生的光强失衡，这将进一步减轻反压缩对系统性能的影响。这些关联特性凸显了纠缠双梳光谱学的复杂性，同时也证明了其实现显著计量优势的潜力。

最后，我们将本研究与近期报道的两项量子双梳光谱学实验27,50进行对比。双梳光谱学的一个关键性能指标为品质因数，定义为 S N R × M / τ \sqrt{SNR ×M / \sqrt{\tau}} SNR×M/τ ，其中 M = 2 N M=2N M=2N为总梳齿数，SNR为振幅信噪比， τ \tau τ为积分时间14。研究表明，在非对称双梳光谱学方案中，仅有信号梳对样品进行探测，而另一束光强高得多的梳作为外差探测器的本地振荡器，在样品接收功率给定的情况下，该方案的品质因数可达经典双梳光谱学的极限26。因此，利用纠缠提升信噪比，可使我们提出的非对称纠缠双梳光谱学突破经典双梳光谱学的根本极限。文献27的实验具有创新性，实现了大光谱覆盖和高分辨率，但在其对称双梳光谱学方案中，在相同功率约束下，将光功率均匀分配给两束梳可实现最优品质因数。因此，实验中两束梳的功率严重失衡，导致其品质因数低于经典极限（见附录B）。文献50的实验采用非对称双梳光谱学方案，由经典梳探测样品，压缩光作为本地振荡器。尽管该配置因频率转换效率低具有一定的实际优势，但无法突破经典双梳光谱学的根本极限51。

致谢

本研究得到美国海军研究办公室资助（项目编号：N00014-23-1-2296）、美国国家科学基金会资助（项目编号：2317471、2326746）以及密歇根大学的支持。庄群涛和石昊还得到美国空军科学研究办公室多学科大学研究计划（项目编号：FA9550-24-1-0349）和美国国防高级研究计划局（项目编号：D24AC00153-02）的资助。阿卜杜勒卡里姆·哈里里得到国家电信和信息安全公司的奖学金支持。感谢吴健就相位锁定问题提供的讨论。

数据可用性

支持本文研究结果的数据因法律限制无法公开发布，可向作者合理索取。

附录A 实验细节

A1 纠缠双梳光谱学装置

图7展示了详细的实验装置示意图。1550纳米光纤激光器（NKT Photonics Koheras BASIK）产生30毫瓦的激光，经光纤电光相位调制器调制，调制器由88兆赫信号驱动，产生边带用于通过庞德-德雷弗-霍尔技术锁定光腔。调制后的激光经掺铒光纤放大器放大至约1.5瓦，然后耦合至自由空间。1550纳米激光被导入三镜腔进行时空模式清洁，并锁定在最大透射率位置。模式清洁腔的输出分为两路：一路作为二次谐波产生的泵浦光，另一路经过第二个模式清洁腔后，再分为三路，分别作为光学参量振荡器的种子光、经典梳和外差测量的本地振荡器梳。

经典梳由两个光纤电光相位调制器产生：一个由17.569吉赫信号驱动，产生梳齿；另一个由锁相放大器产生的100千赫信号驱动，产生边带用于将经典梳锁定至纠缠梳。在与纠缠梳发生干涉前，经典梳先通过可编程光学滤波器（波整形器），以调控纠缠信号梳每个梳齿的光强和相位。波整形器的作用包括：平衡每个模式对中两个梳齿的光强；有意降低除用于锁定的中央梳齿外所有梳齿的功率，以抑制射频拍频信号中的相位噪声（图3(b)和3©）；优化每个梳齿的相位，以最大化射频拍频信号强度；此外，还为解决梳齿混叠的双次测量配置梳齿相位。

二次谐波产生腔为半单片结构，包含一个在775纳米波段低反射、1550纳米波段高反射的曲面镜，以及一块周期极化磷酸氧钛钾晶体。该腔通过88兆赫边带锁定，并通过二阶倍频产生775纳米激光。775纳米激光经模式清洁腔后，注入包含相同周期极化磷酸氧钛钾晶体的光学参量振荡器腔。光学参量振荡器腔的曲面镜在775纳米波段高反射、1550纳米波段中等反射。三个模式清洁腔通过采集输入耦合镜的反射光进行锁定，而二次谐波产生腔和光学参量振荡器的1550、775纳米波段锁定则通过采集透射光实现。

为产生纠缠梳，弱1550纳米种子光经自由空间相位调制器调制，调制器由40兆赫信号驱动，产生边带用于参量放大锁定。光学参量振荡器腔通过775纳米泵浦光的66兆赫边带锁定，该边带通过泵浦输入路径上的双色分束器透射。在775纳米泵浦光的作用下，光学参量振荡器通过自发参量下转换在1550纳米波段产生压缩光；当通过相位锁定实现参量放大时，种子光的光子统计特性从相干态转变为位移相位压缩态。光学参量振荡器输出的量子光包括中心频率处的单模压缩态，以及由双模压缩真空态对组成的纠缠梳。纠缠梳产生后，与经典梳在99:1分束器上发生干涉，将每个双模压缩真空态对转换为位移双模压缩态。

A2 纠缠梳的表征

本地振荡器梳的制备方式与经典梳类似，使用独立的相位调制器和波整形器。调整本地振荡器梳的振幅和相位，使其与双模压缩真空态的压缩正交分量对准，实现所有纠缠梳齿最大压缩的同时探测。若振幅平衡不当，本地振荡器梳与信号梳不匹配，将导致观测到的压缩程度降低；此外，相位对准不当会导致不同模式的压缩和反压缩正交分量混合，使纠缠梳整体的亚标准量子极限探测能力失效。图8(a)-(f)展示了中央梳齿和五个双模对的压缩和反压缩正交分量测量结果；图8(g)证明了所有双模压缩态压缩正交分量的同时探测能力；图8(h)展示了用于获取图3-5的3-21兆赫目标光谱范围内的量子优势。

本实验中，产生的纠缠信号梳总功率为4纳瓦（图3(a)），包含10个信号梳齿和一个用于锁定纠缠梳与经典信号梳相位的中央梳齿，中央梳齿功率为2微瓦。为降低拍频信号的相位噪声，将信号梳功率降至亚纳瓦级别（图3(b)和3©）。探测纠缠信号梳所用的本地振荡器梳，每个梳齿的平均功率为1.8毫瓦。

A3 双梳光谱的采集

图3(a)-©和图4(b)-(d)中的双梳光谱，均通过对平衡接收器的光电流差值时域信号采样得到。采样速率为100兆赫，采样时长为0.5秒，对记录的数据进行后处理，得到对应的频域光谱。图3(a)的后处理采用10千赫的分辨率带宽和5000幅干涉图；与之不同，图3(b)和3©采用200赫兹的分辨率带宽和100幅干涉图，图4(b)-(d)采用100赫兹的分辨率带宽和50幅干涉图。

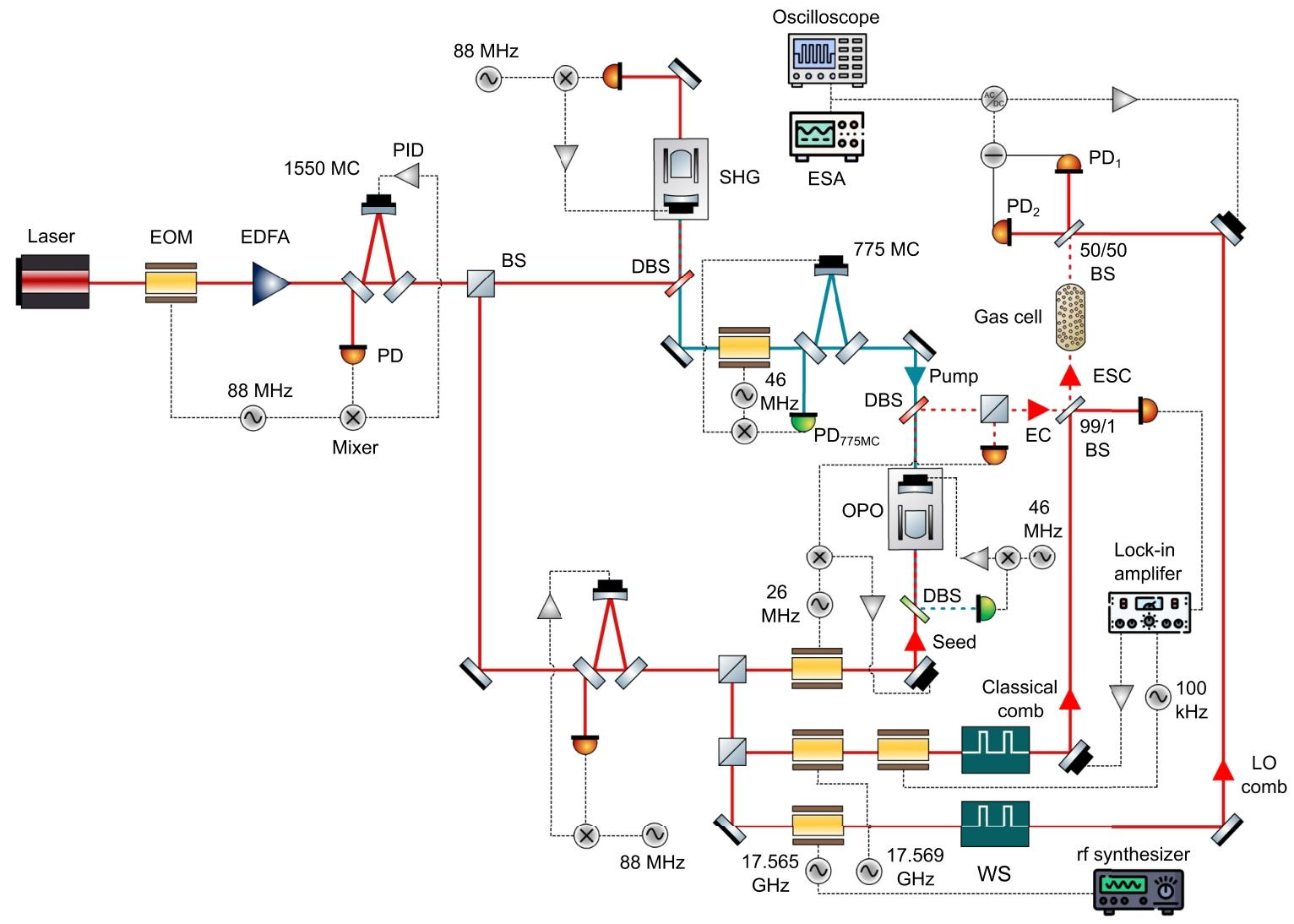
【图7 实验装置示意图】

1550纳米纠缠梳由阈值以下工作的双共振光学参量振荡器产生。EOM：电光调制器；EDFA：掺铒光纤放大器；1550MC：1550纳米光的三镜时空模式清洁腔；PID：比例-积分-微分控制器；BS：分束器；DBS：双色分束器；SHG：二次谐波产生；PD：光电二极管。为产生纠缠信号梳，纠缠梳与经电光调制器和波整形器（WS）产生的经典梳在99:1分束器上发生干涉。为锁定经典梳与纠缠梳之间的相位，锁相放大器驱动经典梳光路中的第二个电光调制器产生边带，作为误差信号，由比例-积分-微分控制器实现相位稳定。纠缠信号梳穿过气体池后，与本地振荡器梳发生外差干涉。平衡探测得到的光电流差值由电子频谱分析仪（ESA）分析，用于系统的实时优化；同时由示波器采集，用于获取干涉图。

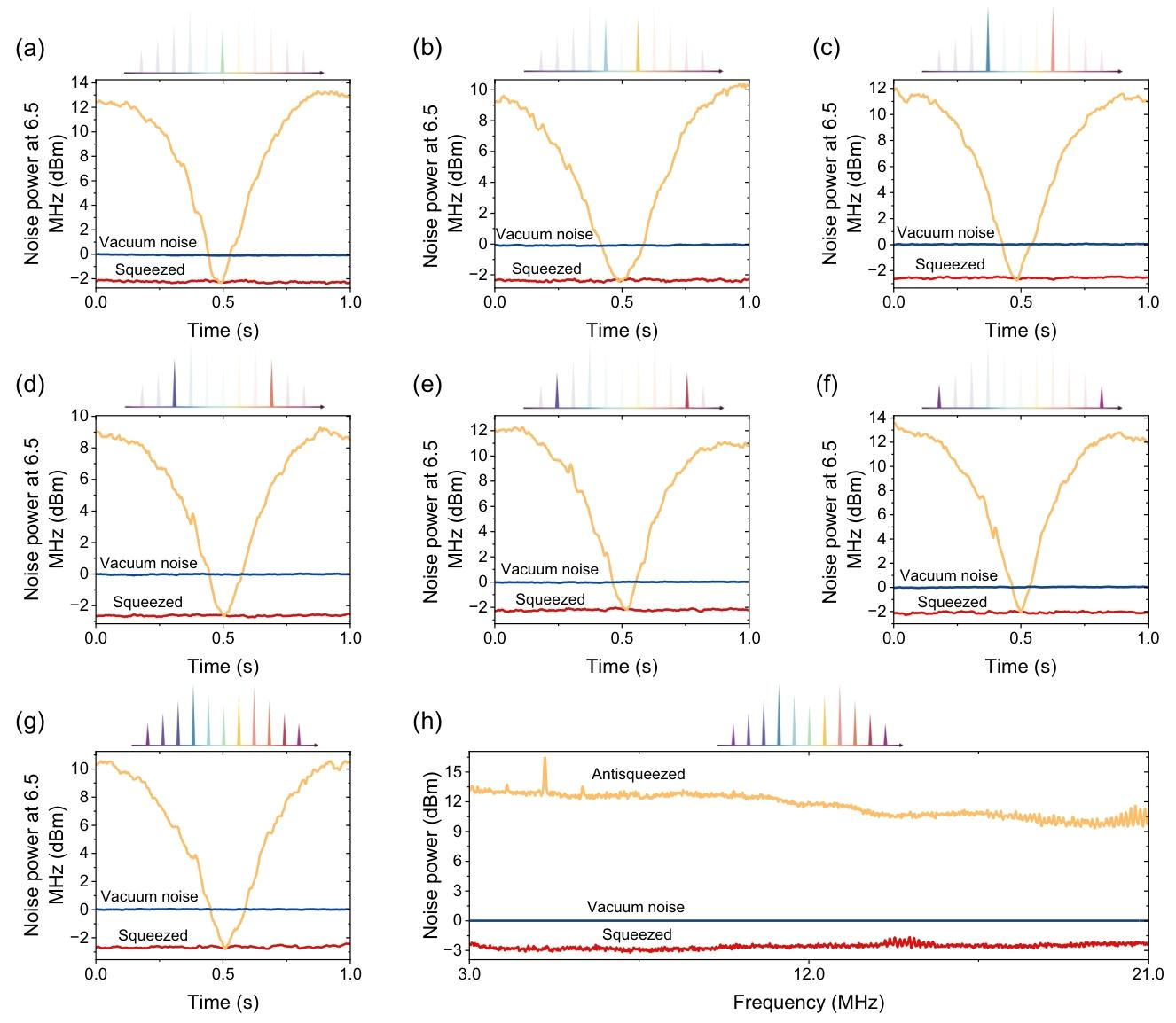
【图8 利用电子频谱分析仪在6.5兆赫频率下对纠缠梳的零跨度测量】

(a) 关闭所有其他梳齿，利用本地振荡器梳的中央梳齿测量中央梳齿的结果；(b) 第一个纠缠模式对的测量结果；© 第二个纠缠模式对的测量结果；(d) 第三个纠缠模式对的测量结果；(e) 第四个纠缠模式对的测量结果；(f) 第五个纠缠模式对的测量结果；(g) 开启所有纠缠梳齿的测量结果，测量得到的压缩因子为2.1-2.8分贝，反压缩因子为9.3-13.3分贝；(h) 所有梳齿同时探测时，3-21兆赫光谱范围内的压缩和反压缩水平，探测器的电子噪声比真空噪声低18分贝，分辨率带宽设置为300千赫，视频带宽设置为300赫兹。

附录B 纠缠双梳光谱学的理论

本附录建立了量子理论模型，推导了光电流测量输出的公式，并给出了信息承载均值、量子测量噪声的推导过程，最终得到信噪比公式。

B1 输入和信道的建模

遵循文献26的推导方法，我们总结了具有 2 N + 1 2N+1 2N+1个梳齿的双梳光谱学量子理论，其中包括一个仅用于相位锁定的中央梳齿，以及对称分布在中央梳齿两侧、用于光谱学测量的 N N N对梳齿，如图9所示。假设每个梳齿均为有效单色光，即频率梳的线宽小于采集时间 T T T对应的最小可分辨线宽 1 / T 1/T 1/T，因此每个激发的梳齿可视为单个频率仓模式。要求 f r e p f_{rep} frep、 δ f r e f > 1 / T \delta f_{ref}>1/T δfref>1/T，以避免混叠现象。由于本地振荡器梳的光强远大于信号梳，将其作经典处理，完全由频率 n f r e p n f_{rep} nfrep处的梳齿振幅 B n B_n Bn表征（ − N ≤ n ≤ N -N ≤n ≤N −N≤n≤N）；相反，信号梳由梳齿振幅 { A n } \{A_n\} {An}和零均值量子涨落模式 { a ^ n , m } \{\hat{a}{n,m}\} {a^n,m}表征。信号的功率为 P ≡ ℏ ω c ∑ n = − N , n ≠ 0 N ∣ A n ∣ 2 / T P \equiv \hbar \omega_c \sum{n=-N, n ≠0}^{N}|A_{n}|^{2} / T P≡ℏωc∑n=−N,n=0N∣An∣2/T，其中 ω c \omega_c ωc为光载波的角频率。

我们对量子涨落模式进行正式定义：由湮灭算符 a ^ n , m \hat{a}{n,m} a^n,m表示的场的频率模式满足对易关系 a \^ n , m , a \^ n , m † = 1 \\hat{a}_{n,m}, \\hat{a}_{n,m}\^{\\dagger}=1 a\^n,m,a\^n,m†=1，其余所有对易子均为0。双下标 n ∈ − N , N n \in-N, N n∈−N,N和 m ∈ − N , N m \in-N, N m∈−N,N表示频率为 n f r e p + m δ f r e p n f{rep}+m \delta f_{rep} nfrep+mδfrep的模式，其中 n n n表示模式所属的梳齿， m m m进一步表示该模式相对于梳齿的边带位置。由于 δ f r e p ≫ 1 / T \delta f_{rep} \gg 1/T δfrep≫1/T，不同梳齿周围的边带模式不会重叠。这些 N 2 N^2 N2个模式与外差测量得到的纠缠双梳光谱学数据相关。在经典双梳光谱学中，所有模式的统计特性均为真空态，导致外差测量存在经典散粒噪声极限；相反，纠缠双梳光谱学中不同模式间的纠缠使其能够突破该经典极限，具体推导如下。

将待测量的样品吸收过程建模为玻色损耗信道的张量积，该信道的输入-输出关系为：均值满足 A n → κ n A n e i α n A_n \to \sqrt{\kappa_n} A_n e^{i \alpha_n} An→κn Aneiαn，噪声模式满足：
a ^ n , m ′ = κ n e i α n a ^ n , m + 1 − κ n e ^ n , m (B1) \hat{a}{n, m}'=\sqrt{\kappa{n}} e^{i \alpha_{n}} \hat{a}{n, m}+\sqrt{1-\kappa{n}} \hat{e}_{n, m} \tag{B1} a^n,m′=κn eiαna^n,m+1−κn e^n,m(B1)

其中， κ n \kappa_n κn和 α n \alpha_n αn分别为频率 n f r e p n f_{rep} nfrep附近吸收光谱的功率透射率和相移。

【 图9 纠缠信号梳和本地振荡器梳的频率模式示意图】

B2 平衡外差光电流

在平衡外差测量中，本地振荡器梳与反射的信号梳在平衡分束器上发生拍频，分束器的输出分别入射至光电二极管，将得到的光电流相减，得到射频光电流（记为 N ^ A C \hat{N}{AC} N^AC），并舍弃直流分量。在强本地振荡器极限下，即 B n ≫ A m B_n \gg A_m Bn≫Am（ ∀ n , m \forall n,m ∀n,m），平衡外差光电流在射频频率 m δ f r e p m \delta f{rep} mδfrep处的离散傅里叶光谱为：
N ^ m A C = ∑ n = − N N B n ∗ A ^ n , m ′ + B n A ^ n , − m ′ † (B2) \hat{N}{m}^{AC}=\sum{n=-N}^{N} B_{n}^{*} \hat{A}{n, m}'+B{n} \hat{A}_{n,-m}^{\prime \dagger} \tag{B2} N^mAC=n=−N∑NBn∗A^n,m′+BnA^n,−m′†(B2)

其中，
A ^ n , k ′ = a ^ n , k ′ + δ n , k κ n A n e i α n (B3) \hat{A}{n, k}'=\hat{a}{n, k}'+\delta_{n, k} \sqrt{\kappa_{n}} A_{n} e^{i \alpha_{n}} \tag{B3} A^n,k′=a^n,k′+δn,kκn Aneiαn(B3)

为频率 n f r e p + k δ f r e p n f_{rep}+k \delta f_{rep} nfrep+kδfrep处的反射信号光谱。式中，克罗内克函数 δ n , k \delta_{n,k} δn,k在 k = n k=n k=n时为1，其余情况为0；信道输出噪声 a ^ n , k ′ \hat{a}{n,k}' a^n,k′由公式(B1)定义。该光电流包含均值 < N ^ m A C > <\hat{N}{m}^{AC}> <N^mAC>和零均值噪声 ∑ ^ m A C \hat{\sum }{m}^{AC} ∑^mAC两部分：
N ^ m A C = < N ^ m A C > + ∑ ^ m A C (B4) \hat{N}{m}^{AC}=\left<\hat{N}{m}^{AC}\right>+\hat{\sum}{m}^{AC} \tag{B4} N^mAC=⟨N^mAC⟩+∑^mAC(B4)

光学参量振荡器的输出在 a ^ n , m \hat{a}{n,m} a^n,m和 a ^ − n , − m \hat{a}{-n,-m} a^−n,−m之间形成双模压缩态对。令 a ^ n , m → a ^ 1 \hat{a}_{n,m} \to \hat{a}1 a^n,m→a^1、 a ^ − n , − m → a ^ 2 \hat{a}{-n,-m} \to \hat{a}2 a^−n,−m→a^2，在 κ n → 1 \kappa_n \to 1 κn→1的极限下，可发现输入对噪声 ∑ ^ m A C \hat{\sum }{m}^{AC} ∑^mAC的贡献与 ( a ^ 1 + a ^ 2 † ) / 2 = ( q ^ 1 + q ^ 2 ) / 2 + i ( p ^ 1 − p ^ 2 ) / 2 = q ^ + + i p ^ − (\hat{a}_1+\hat{a}_2^\dagger)/\sqrt{2}=(\hat{q}_1+\hat{q}_2)/\sqrt{2}+i(\hat{p}1-\hat{p}2)/\sqrt{2}=\hat{q}++i\hat{p}- (a^1+a^2†)/2 =(q^1+q^2)/2 +i(p^1−p^2)/2 =q^++ip^−成正比。因此，借助双模压缩态，可实现两个正交分量噪声的抑制，这一特性源于模间纠缠，且由于 q \^ + , p \^ − = 0 \\hat{q}_+,\\hat{p}_-=0 q\^+,p\^−=0，该过程不违反海森堡不确定性原理。后续将在公式(B15)中推导完整公式。

B3 平衡外差光电流均值的推导

吸收光谱的信息编码在平衡外差光电流的均值中，由公式(B2)可得光电流均值为：
< N ^ m A C > = ∑ n = − N N < B n ∗ A ^ n , m ′ + B n A ^ n , − m ∗ † > = B m ∗ κ m A m e i α m + B − m κ − m A − m ∗ e − i α − m (B5) \begin{aligned} \left<\hat{N}{m}^{AC}\right> & =\sum{n=-N}^{N}\left< B_{n}^{*} \hat{A}{n, m}'+B{n} \hat{A}{n,-m}^{* \dagger}\right> \\ & =B{m}^{*} \sqrt{\kappa_{m}} A_{m} e^{i \alpha_{m}}+B_{-m} \sqrt{\kappa_{-m}} A_{-m}^{*} e^{-i \alpha_{-m}} \tag{B5} \end{aligned} ⟨N^mAC⟩=n=−N∑N⟨Bn∗A^n,m′+BnA^n,−m∗†⟩=Bm∗κm Ameiαm+B−mκ−m A−m∗e−iα−m(B5)

公式(B5)表明，正、负指数梳齿的吸收特性（ κ m e i α m \sqrt{\kappa_m} e^{i \alpha_m} κm eiαm和 κ − m e − i α − m \sqrt{\kappa_{-m}} e^{-i \alpha_{-m}} κ−m e−iα−m）均会对 N ^ m A C \hat{N}_{m}^{AC} N^mAC产生贡献，从而导致混叠现象。接下来我们分析混叠现象的抑制策略。

B4 无先验知识的双次测量

为同时解析正、负指数梳齿的吸收特性（即 κ m e i α m \sqrt{\kappa_m} e^{i \alpha_m} κm eiαm和 κ − m e − i α − m \sqrt{\kappa_{-m}} e^{-i \alpha_{-m}} κ−m e−iα−m），采用双次测量协议：第一次测量按前述方式进行，得到的光电流为：
< N ^ m A C ( 1 ) > = B m ∗ κ m A m e i α m + B − m κ − m A − m ∗ e − i α − m (B6) \left<\hat{N}{m}^{AC(1)}\right>=B{m}^{*} \sqrt{\kappa_{m}} A_{m} e^{i \alpha_{m}}+B_{-m} \sqrt{\kappa_{-m}} A_{-m}^{*} e^{-i \alpha_{-m}} \tag{B6} ⟨N^mAC(1)⟩=Bm∗κm Ameiαm+B−mκ−m A−m∗e−iα−m(B6)

第二次测量中，对正指数经典梳齿施加π相移，即所有 1 ≤ m ≤ N 1 ≤m ≤N 1≤m≤N满足 A m → − A m A_m \to -A_m Am→−Am，再将其与纠缠梳合束，外差测量得到的光电流为：
< N ^ m A C ( 2 ) > = − B m ∗ κ m A m e i α m + B − m κ − m A − m ∗ e − i α − m (B7) \left<\hat{N}{m}^{AC(2)}\right>=-B{m}^{*} \sqrt{\kappa_{m}} A_{m} e^{i \alpha_{m}}+B_{-m} \sqrt{\kappa_{-m}} A_{-m}^{*} e^{-i \alpha_{-m}} \tag{B7} ⟨N^mAC(2)⟩=−Bm∗κm Ameiαm+B−mκ−m A−m∗e−iα−m(B7)

随后，对两次测量结果进行线性组合，即可解出两个光谱分量 κ m e i α m \sqrt{\kappa_m} e^{i \alpha_m} κm eiαm和 κ − m e − i α − m \sqrt{\kappa_{-m}} e^{-i \alpha_{-m}} κ−m e−iα−m。

B5 有先验相位知识的单次测量

当吸收相位光谱 { α m } m = − N N \{\alpha_m\}{m=-N}^N {αm}m=−NN已知或相位较小时，不失一般性，令所有 − N ≤ m ≤ N -N ≤m ≤N −N≤m≤N满足 α m = 0 \alpha_m=0 αm=0。进一步假设，对于 1 < m ≤ N 1<m ≤N 1<m≤N， A m A_m Am为实数；对于 − N ≤ m < − 1 -N ≤m<-1 −N≤m<−1， A m A_m Am为纯虚数，且 B m B_m Bm为实数（可通过波整形器实现），则正、负指数梳齿的吸收特性可在输出光电流的实部和虚部分量中独立解析（实验中分别对应 c o s ( m δ f r e p t ) cos(m \delta f{rep}t) cos(mδfrept)和 s i n ( m δ f r e p t ) sin(m \delta f_{rep}t) sin(mδfrept)）：
< N ^ m A C > = B m κ m A m + i B − m κ − m A − m (B8) \left<\hat{N}{m}^{AC}\right>=B{m} \sqrt{\kappa_{m}} A_{m}+i B_{-m} \sqrt{\kappa_{-m}} A_{-m} \tag{B8} ⟨N^mAC⟩=Bmκm Am+iB−mκ−m A−m(B8)

B6 单侧吸收

若已知吸收仅发生在正指数或负指数梳齿上，单次测量即可推断出吸收光谱。不失一般性，假设负指数梳齿无损耗，即所有 1 ≤ m ≤ N 1 ≤m ≤N 1≤m≤N满足 κ − m = 1 \kappa_{-m}=1 κ−m=1，则公式(B5)中的光电流均值简化为：
< N ^ m A C > = B m ∗ κ m e i α m A m + B − m A − m ∗ (B9) \left<\hat{N}{m}^{AC}\right>=B{m}^{*} \sqrt{\kappa_{m}} e^{i \alpha_{m}} A_{m}+B_{-m} A_{-m}^{*} \tag{B9} ⟨N^mAC⟩=Bm∗κm eiαmAm+B−mA−m∗(B9)

若 A m = A − m = A A_m=A_{-m}=A Am=A−m=A、 B m = B − m = B B_m=B_{-m}=B Bm=B−m=B且 α m = 0 \alpha_m=0 αm=0，则：
< N ^ m A C > = ( 1 + κ m ) A B (B10) \left<\hat{N}{m}^{AC}\right>=\left(1+\sqrt{\kappa{m}}\right) A B \tag{B10} ⟨N^mAC⟩=(1+κm )AB(B10)

B7 平衡外差光电流中量子测量噪声的推导

由于非对称损耗（ κ n ≠ κ − n \kappa_n \neq \kappa_{-n} κn=κ−n），反压缩噪声会混入输出信号中。为简化推导，令所有 − N ≤ n ≤ N -N \leq n \leq N −N≤n≤N满足 α n = 0 \alpha_n=0 αn=0，且 1 ≤ n ≤ N 1 \leq n \leq N 1≤n≤N满足 θ n = 0 \theta_n=0 θn=0、 − N ≤ n ≤ − 1 -N \leq n \leq -1 −N≤n≤−1满足 θ n = π / 2 \theta_n=\pi/2 θn=π/2。可将光电流中的量子噪声 ∑ ^ m A C \hat{\sum}{m}^{AC} ∑^mAC分为两个独立部分： ∑ ^ m A C = ∑ ^ m , Q A C + ∑ ^ m , P A C \hat{\sum}{m}^{AC}=\hat{\sum}{m, Q}^{AC}+\hat{\sum}{m, P}^{AC} ∑^mAC=∑^m,QAC+∑^m,PAC，其中 ∑ ^ m , Q A C \hat{\sum}{m, Q}^{AC} ∑^m,QAC为位置正交分量的贡献， ∑ ^ m , P A C \hat{\sum}{m, P}^{AC} ∑^m,PAC为动量正交分量的贡献。在强本地振荡器极限下， ∑ ^ m , Q A C \hat{\sum}{m, Q}^{AC} ∑^m,QAC为：
2 ∑ ^ m , Q A C ≃ ( B 0 ∗ q ^ 0 , m ′ + B 0 q ^ 0 , − m ′ ) + ∑ n = 1 N ( B n ∗ q \^ n , m ′ + B n q \^ n , − m ′ ) + ( B − n q \^ − n , − m ′ + B − n ∗ q \^ − n , m ′ ) \begin{aligned} \sqrt{2} \hat{\sum}{m, Q}^{AC} \simeq & \left(B_{0}^{*} \hat{q}{0, m}'+B{0} \hat{q}{0,-m}'\right) \\ & +\sum{n=1}^{N}\left\\left(B_{n}\^{\*} \\hat{q}_{n, m}'+B_{n} \\hat{q}_{n,-m}'\\right)\\right. \\\\ \& \\left.+\\left(B_{-n} \\hat{q}_{-n,-m}'+B_{-n}\^{\*} \\hat{q}_{-n, m}'\\right)\\right \end{aligned} 2 ∑^m,QAC≃(B0∗q^0,m′+B0q^0,−m′)+n=1∑N(Bn∗q\^n,m′+Bnq\^n,−m′)+(B−nq\^−n,−m′+B−n∗q\^−n,m′)

同理，
2 ∑ ^ m , P A C ≃ i { ( B 0 ∗ p ^ 0 , m ′ − B 0 p ^ 0 , − m ′ ) + ∑ n = 1 N ( B n ∗ p \^ n , m ′ − B n p \^ n , − m ′ ) + ( − B − n p \^ − n , − m ′ + B − n ∗ p \^ − n , m ′ ) } , (B12) \begin{aligned} \sqrt{2} \hat{\sum}{m, P}^{AC} \simeq & i\left\{\left(B{0}^{*} \hat{p}{0, m}'-B{0} \hat{p}{0,-m}'\right)\right. \\ & +\sum{n=1}^{N}\left\\left(B_{n}\^{\*} \\hat{p}_{n, m}'-B_{n} \\hat{p}_{n,-m}'\\right)\\right. \\\\ \& \\left.\\left.+\\left(-B_{-n} \\hat{p}_{-n,-m}'+B_{-n}\^{\*} \\hat{p}_{-n, m}'\\right)\\right\right\}, \tag{B12} \end{aligned} 2 ∑^m,PAC≃i{(B0∗p^0,m′−B0p^0,−m′)+n=1∑N(Bn∗p\^n,m′−Bnp\^n,−m′)+(−B−np\^−n,−m′+B−n∗p\^−n,m′)},(B12)

其中， q ^ n , m ′ ≡ 2 Re a ^ n , m ′ \hat{q}{n, m}' \equiv \sqrt{2} \text{Re}\hat{a}{n, m}' q^n,m′≡2 Rea^n,m′、 p ^ n , m ′ ≡ 2 Im a ^ n , m ′ \hat{p}{n, m}' \equiv \sqrt{2} \text{Im}\hat{a}{n, m}' p^n,m′≡2 Ima^n,m′，且 a ^ n , m ′ = κ n a ^ n , m + 1 − κ n e ^ n , m \hat{a}{n,m}'=\sqrt{\kappa_n} \hat{a}{n,m}+\sqrt{1-\kappa_n} \hat{e}{n,m} a^n,m′=κn a^n,m+1−κn e^n,m（由公式(B1)定义）。为描述双模压缩态对 a ^ n , m \hat{a}{n,m} a^n,m和 a ^ − n , − m \hat{a}{-n,-m} a^−n,−m，定义共模和差模，其正交算符为 q ^ n , m ± ≡ q ^ n , m ± q ^ − n , − m \hat{q}{n, m}^{\pm} \equiv \hat{q}{n, m} \pm \hat{q}{-n,-m} q^n,m±≡q^n,m±q^−n,−m、 p ^ n , m ± ≡ p ^ n , m ± p ^ − n , − m \hat{p}{n, m}^{\pm} \equiv \hat{p}{n, m} \pm \hat{p}_{-n,-m} p^n,m±≡p^n,m±p^−n,−m。

双模压缩可通过压缩和反压缩正交分量描述：
Var { q ^ n , m + } = Var { p ^ n , m − } = 1 / G n , \text{Var}\left\{ \hat{q}{n, m}^{+}\right\} = \text{Var}\left\{ \hat{p}{n, m}^{-}\right\} = 1 / G_{n}, Var{q^n,m+}=Var{p^n,m−}=1/Gn,
Var { q ^ n , m − } = Var { p ^ n , m + } = G n ′ , (B13) \text{Var}\left\{ \hat{q}{n, m}^{-}\right\} = \text{Var}\left\{ \hat{p}{n, m}^{+}\right\} = G_{n}^{\prime}, \tag{B13} Var{q^n,m−}=Var{p^n,m+}=Gn′,(B13)

其中， G n > 1 G_n>1 Gn>1为压缩量， G n ′ > 1 G_n'>1 Gn′>1为反压缩量。由于损耗的存在， G n ′ ≠ G n > 1 G_n' \neq G_n>1 Gn′=Gn>1。

基于位置正交分量（Q）和动量正交分量（P）贡献的对称性，我们以动量正交分量为例进行信噪比分析。对 q ^ ± \hat{q}^{\pm} q^±和 p ^ ± \hat{p}^{\pm} p^±进行变换后，公式(B12)可改写为：
2 ∑ ^ m , P A C / i ≃ B 0 κ 0 p ^ 0 , m − + ∑ n = 1 N κ n ( B n ∗ p \^ n , m + + p \^ n , m − 2 − B n p \^ n , − m + + p \^ n , − m − 2 ) + κ − n ( − B − n p \^ n , m + − p \^ n , m − 2 + B − n ∗ p \^ n , − m + − p \^ n , − m − 2 ) + 环境噪声 = B 0 κ 0 p ^ 0 , m − + ∑ n = 1 N 1 2 ( κ n B n ∗ − κ − n B − n ) p \^ n , m + + ( − κ n B n + κ − n B − n ∗ ) p \^ n , − m + + ( κ n B n ∗ + κ − n B − n ) p \^ n , m − + ( − κ n B n − κ − n B − n ∗ ) p \^ n , − m − + 环境噪声 , (B14) \begin{aligned} \sqrt{2} \hat{\sum}{m, P}^{AC} / i \simeq & B{0} \sqrt{\kappa_{0}} \hat{p}{0, m}^{-}+\sum{n=1}^{N}\left\\sqrt{\\kappa_{n}}\\left(B_{n}\^{\*} \\frac{\\hat{p}_{n, m}\^{+}+\\hat{p}_{n, m}\^{-}}{2}-B_{n} \\frac{\\hat{p}_{n,-m}\^{+}+\\hat{p}_{n,-m}\^{-}}{2}\\right)\\right. \\\\ \& \\left.+\\sqrt{\\kappa_{-n}}\\left(-B_{-n} \\frac{\\hat{p}_{n, m}\^{+}-\\hat{p}_{n, m}\^{-}}{2}+B_{-n}\^{\*} \\frac{\\hat{p}_{n,-m}\^{+}-\\hat{p}_{n,-m}\^{-}}{2}\\right)\\right+\text{环境噪声} \\ = & B_{0} \sqrt{\kappa_{0}} \hat{p}{0, m}^{-}+\sum{n=1}^{N} \frac{1}{2}\left\\left(\\sqrt{\\kappa_{n}} B_{n}\^{\*}-\\sqrt{\\kappa_{-n}} B_{-n}\\right) \\hat{p}_{n, m}\^{+}+\\left(-\\sqrt{\\kappa_{n}} B_{n}+\\sqrt{\\kappa_{-n}} B_{-n}\^{\*}\\right) \\hat{p}_{n,-m}\^{+}\\right. \\\\ \& \\left.+\\left(\\sqrt{\\kappa_{n}} B_{n}\^{\*}+\\sqrt{\\kappa_{-n}} B_{-n}\\right) \\hat{p}_{n, m}\^{-}+\\left(-\\sqrt{\\kappa_{n}} B_{n}-\\sqrt{\\kappa_{-n}} B_{-n}\^{\*}\\right) \\hat{p}_{n,-m}\^{-}\\right+\text{环境噪声}, \tag{B14} \end{aligned} 2 ∑^m,PAC/i≃=B0κ0 p^0,m−+n=1∑Nκn (Bn∗2p\^n,m++p\^n,m−−Bn2p\^n,−m++p\^n,−m−)+κ−n (−B−n2p\^n,m+−p\^n,m−+B−n∗2p\^n,−m+−p\^n,−m−)+环境噪声B0κ0 p^0,m−+n=1∑N21(κn Bn∗−κ−n B−n)p\^n,m++(−κn Bn+κ−n B−n∗)p\^n,−m++(κn Bn∗+κ−n B−n)p\^n,m−+(−κn Bn−κ−n B−n∗)p\^n,−m−+环境噪声,(B14)

其中，环境噪声的方差为 ∑ n = − N N ( 1 − κ n ) B n 2 \sum_{n=-N}^{N}(1-\kappa_{n}) B_{n}^{2} ∑n=−NN(1−κn)Bn2。最终，动量正交分量贡献的方差为：
Var ∑ ^ m , P A C = 1 2 κ 0 ∣ B 0 ∣ 2 1 G 0 + ∑ n = 1 N 1 4 ∣ κ n B n ∗ − κ − n B − n ∣ 2 G n ′ + ∣ κ n B n ∗ + κ − n B − n ∣ 2 / G n + 1 2 ∑ n = − N N ( 1 − κ n ) ∣ B n ∣ 2 , \begin{aligned} \text{Var}\hat{\sum}{m, P}^{AC}= & \frac{1}{2} \kappa{0}\left|B_{0}\right|^{2} \frac{1}{G_{0}}+\sum_{n=1}^{N} \frac{1}{4}\left\\left\|\\sqrt{\\kappa_{n}} B_{n}\^{\*}-\\sqrt{\\kappa_{-n}} B_{-n}\\right\|\^{2} G_{n}'\\right. \\\\ \& \\left.+\\left\|\\sqrt{\\kappa_{n}} B_{n}\^{\*}+\\sqrt{\\kappa_{-n}} B_{-n}\\right\|\^{2} / G_{n}\\right+\frac{1}{2} \sum_{n=-N}^{N}\left(1-\kappa_{n}\right)\left|B_{n}\right|^{2}, \end{aligned} Var∑^m,PAC=21κ0∣B0∣2G01+n=1∑N41∣κn Bn∗−κ−n B−n∣2Gn′+∣κn Bn∗+κ−n B−n∣2/Gn+21n=−N∑N(1−κn)∣Bn∣2,

位置正交分量贡献的方差形式与此类似。将无压缩的真空态输入（ G n = G n ′ = 1 G_n=G_n'=1 Gn=Gn′=1）代入公式(B15)，可得到散粒（真空）噪声极限：
σ SHOT 2 = Var ∑ ^ m , Q A C ∣ G n = G n ′ = 1 = Var ∑ ^ m , P A C ∣ G n = G n ′ = 1 = 1 2 ∑ n = − N N κ n ∣ B n ∣ 2 + ( 1 − κ n ) ∣ B n ∣ 2 = 1 2 ∑ n = − N N ∣ B n ∣ 2 , (B16) \begin{aligned} \sigma_{\text{SHOT}}^{2}= & \left.\text{Var}\hat{\sum}{m, Q}^{AC}\right|{G_{n}=G_{n}'=1}=\left.\text{Var}\hat{\sum}{m, P}^{AC}\right|{G_{n}=G_{n}'=1} \\ = & \frac{1}{2} \sum_{n=-N}^{N} \kappa_{n}\left|B_{n}\right|^{2}+\left(1-\kappa_{n}\right)\left|B_{n}\right|^{2}=\frac{1}{2} \sum_{n=-N}^{N}\left|B_{n}\right|^{2}, \tag{B16} \end{aligned} σSHOT2==Var∑^m,QAC Gn=Gn′=1=Var∑^m,PAC Gn=Gn′=121n=−N∑Nκn∣Bn∣2+(1−κn)∣Bn∣2=21n=−N∑N∣Bn∣2,(B16)

该极限由本地振荡器梳的总功率 P LO = ℏ ω c ∑ n = − N N ∣ B n ∣ 2 / T P_{\text{LO}}=\hbar \omega_{c} \sum_{n=-N}^{N}|B_{n}|^{2} / T PLO=ℏωc∑n=−NN∣Bn∣2/T决定。

B8 信噪比分析

为计算第 m m m个梳齿的信噪比，定义射频光电流中可由 κ m e i α m \sqrt{\kappa_m} e^{i \alpha_m} κm eiαm调制的信号功率为 ∣ B m ∗ κ m A m ∣ 2 |B_{m}^{*} \sqrt{\kappa_{m}} A_{m}|^{2} ∣Bm∗κm Am∣2。对于已知相位的单次测量，光电流均值由公式(B8)给出，此时信号功率定义为第 m m m个梳齿光电流实部测量均值的功率；对于已知单侧吸收的测量（光电流均值由公式(B9)给出），可采用单侧信号梳（即 m ≤ 0 m \leq 0 m≤0时 A m = 0 A_m=0 Am=0）实现。假设 α m \alpha_m αm、 α − m → 0 \alpha_{-m} \to 0 α−m→0，结合公式(B5)和(B15)，可得到第 m m m个梳齿光谱 κ m \sqrt{\kappa_m} κm 估算的功率信噪比：
SNR m 2 = ∣ B m ∗ κ m A m ∣ 2 1 2 κ 0 ∣ B 0 ∣ 2 1 G 0 + ∑ n = 1 N 1 4 ∣ κ n B n ∗ − κ − n B − n ∣ 2 G n ′ + ∣ κ n B n ∗ + κ − n B − n ∣ 2 / G n + 真空噪声 , (B17) \text{SNR}{m}^{2}=\frac{\left|B{m}^{*} \sqrt{\kappa_{m}} A_{m}\right|^{2}}{\frac{1}{2} \kappa_{0}\left|B_{0}\right|^{2} \frac{1}{G_{0}}+\sum_{n=1}^{N} \frac{1}{4}\left\\left\|\\sqrt{\\kappa_{n}} B_{n}\^{\*}-\\sqrt{\\kappa_{-n}} B_{-n}\\right\|\^{2} G_{n}'+\\left\|\\sqrt{\\kappa_{n}} B_{n}\^{\*}+\\sqrt{\\kappa_{-n}} B_{-n}\\right\|\^{2} / G_{n}\\right+\text{真空噪声}}, \tag{B17} SNRm2=21κ0∣B0∣2G01+∑n=1N41 κn Bn∗−κ−n B−n 2Gn′+ κn Bn∗+κ−n B−n 2/Gn+真空噪声 Bm∗κm Am 2,(B17)

其中， 真空噪声 = 1 2 ∑ n = − N N ( 1 − κ n ) ∣ B n ∣ 2 \text{真空噪声}=\frac{1}{2} \sum_{n=-N}^{N}(1-\kappa_{n})|B_{n}|^{2} 真空噪声=21∑n=−NN(1−κn)∣Bn∣2，源于样品吸收引入的真空噪声。

纠缠信号梳的单个梳齿光强过弱，无法直接精确测量。因此，在已知 B m B_m Bm、 κ − m = 1 \kappa_{-m}=1 κ−m=1的校准测量中，通过射频光电流推断其功率。利用实验数据推断出 A m A_m Am后，可得到正文图6所示的绝对信噪比曲线。

B9 双梳光谱学的经典极限

双梳光谱学的信噪比由纠缠结构和测量方案共同决定，以下给出两种典型情况的分析：

B9.1 纠缠双梳光谱学与外差接收器

本文提出的纠缠双梳光谱学采用非对称结构，仅有信号梳入射至样品，样品接收的总功率为 P = ℏ ω c A 2 M / T P=\hbar \omega_c A^2 M / T P=ℏωcA2M/T，并采用外差接收器进行测量，其振幅信噪比由公式(B17)推导得出。假设梳光谱均匀（ A n = A A_n=A An=A、 B n = B B_n=B Bn=B）且弱吸收（ κ n → 1 \kappa_n \to 1 κn→1），则非对称双梳光谱学的经典信噪比极限为：
( SNR CL asym ) 2 = A 2 M / 2 = 2 P T M 2 ℏ ω c . (B18) \left(\text{SNR}{\text{CL}}^{\text{asym}}\right)^{2}=\frac{A^{2}}{M / 2}=\frac{2 P T}{M^{2} \hbar \omega{c}}. \tag{B18} (SNRCLasym)2=M/2A2=M2ℏωc2PT.(B18)

B9.2 压缩双梳光谱学与分束接收器

文献27提出的压缩双梳光谱学首先将信号梳与本地振荡器梳在50:50分束器上合束，产生总功率 P = ℏ ω c ( A 2 + B 2 ) M / ( 2 T ) P=\hbar \omega_c(A^2+B^2) M / (2T) P=ℏωc(A2+B2)M/(2T)的光入射至样品，随后采用分束接收器进行测量。在这种对称双梳光谱学结构中14，两束梳均穿过样品，且通常携带相当的光功率。因此，不再假设本地振荡器梳的光强远大于信号梳，即 A n A_n An和 B m B_m Bm可处于同一数量级。假设梳光谱均匀（ A n = A A_n=A An=A、 B n = B B_n=B Bn=B）且弱吸收（ κ n → 1 \kappa_n \to 1 κn→1），结合文献52的推导，对称双梳光谱学的信噪比为：
( SNR sym ) 2 = 1 M A 2 B 2 2 B 2 σ B 2 + 2 A 2 σ A 2 , (B19) \left(\text{SNR}^{\text{sym}}\right)^{2}=\frac{1}{M} \frac{A^{2} B^{2}}{2 B^{2} \sigma_{B}^{2}+2 A^{2} \sigma_{A}^{2}}, \tag{B19} (SNRsym)2=M12B2σB2+2A2σA2A2B2,(B19)

其中，因子2源于正、负指数梳齿的拍频贡献； σ A 2 ≡ varRe a ^ n , m \sigma_A^2 \equiv \text{varRe}\hat{a}{n,m} σA2≡varRea^n,m为已知相位的场涨落， σ B \sigma_B σB同理。需注意，文献52考虑相位未知的情况，将涨落定义为 σ A 2 ≡ varRe a ^ n , m + varIm a ^ n , m \sigma_A^2 \equiv \text{varRe}\hat{a}{n,m}+\text{varIm}\hat{a}{n,m} σA2≡varRea^n,m+varIma^n,m，此时噪声包含两个正交分量，功率信噪比减半。将散粒噪声极限 σ A 2 = σ B 2 = 1 / 4 \sigma_A^2=\sigma_B^2=1/4 σA2=σB2=1/4代入，文献27实验装置可实现的经典信噪比为：
( SNR C sym ) 2 = 1 M 2 A 2 B 2 B 2 + A 2 , (B20) \left(\text{SNR}{C}^{\text{sym}}\right)^{2}=\frac{1}{M} \frac{2 A^{2} B^{2}}{B^{2}+A^{2}}, \tag{B20} (SNRCsym)2=M1B2+A22A2B2,(B20)

令两束梳的功率相等（ A 2 = B 2 = P T / ( M ℏ ω c ) A^2=B^2=PT/(M\hbar\omega_c) A2=B2=PT/(Mℏωc)），可使该信噪比最大化，得到对称双梳光谱学的经典信噪比极限：
( SNR CL sym ) 2 = P T M 2 ℏ ω c . (B21) \left(\text{SNR}{\text{CL}}^{\text{sym}}\right)^{2}=\frac{P T}{M^{2} \hbar \omega{c}}. \tag{B21} (SNRCLsym)2=M2ℏωcPT.(B21)

然而，文献27的实验中，两束梳的功率差异极大（ A 2 = 15 A^2=15 A2=15毫瓦、 B 2 = 10 B^2=10 B2=10微瓦），即使考虑压缩带来的3分贝提升，其信噪比仍比两束等功率梳实现的经典极限低至少22分贝。在该实验中，测量噪声主要源于光强较强的梳，对其进行压缩可降低噪声基底，而光强极弱的另一束梳对测量噪声无显著贡献。若平衡两束梳的功率，虽可大幅提升信噪比，但额外噪声可能会影响实验系统的量子优势。因此，要突破双梳光谱学的经典极限，需对梳齿间的纠缠结构进行精细设计，这一点在本研究的纠缠双梳光谱学实验中得以实现。

参考文献

1 A. Einstein, B. Podolsky, and N. Rosen, Can quantum-mechanical description of physical reality be considered complete?, Phys. Rev. 47, 777 (1935).

2 E. Schrödinger, Discussion of probability relations between separated systems, in Mathematical Proceedings of the Cambridge Philosophical Society (Cambridge University Press, Cambridge, England, 1935), Vol. 31, pp. 555--563.

3 J. S. Bell, On the Einstein Podolsky Rosen paradox, Phys. Phys. Fiz. 1, 195 (1964).

4 Z. Zhang, C. You, O. S. Magaña-Loaiza, R. Fickler, R. d. J. León-Montiel, J. P. Torres, T. S. Humble, S. Liu, Y. Xia, and Q. Zhuang, Entanglement-based quantum information technology: A tutorial, Adv. Opt. Photonics 16, 60 (2024).

5 R. Jozsa and N. Linden, On the role of entanglement in quantum-computational speed-up, Proc. R. Soc. A 459, 2011 (2003).

6 A. K. Ekert, Quantum cryptography based on Bell's theorem, Phys. Rev. Lett. 67, 661 (1991).

7 T. C. Ralph, Continuous variable quantum cryptography, Phys. Rev. A 61, 010303® (1999).

8 E. S. Polzik, J. Carri, and H. J. Kimble, Spectroscopy with squeezed light, Phys. Rev. Lett. 68, 3020 (1992).

9 Y. Xia, W. Li, W. Clark, D. Hart, Q. Zhuang, and Z. Zhang, Demonstration of a reconfigurable entangled radiofrequency photonic sensor network, Phys. Rev. Lett. 124, 150502 (2020).

10 X. Guo, C. R. Breum, J. Borregaard, S. Izumi, M. V. Larsen, T. Gehring, M. Christandl, J. S. Neergaard-Nielsen, and U. L. Andersen, Distributed quantum sensing in a continuous-variable entangled network, Nat. Phys. 16, 281 (2020).

11 S. Hao, H. Shi, C. N. Gagatsos, M. Mishra, B. Bash, I. Djordjevic, S. Guha, Q. Zhuang, and Z. Zhang, Demonstration of entanglement-enhanced covert sensing, Phys. Rev. Lett. 129, 010501 (2022).

12 T. B. Pittman, Y. H. Shih, D. V. Strekalov, and A. V. Sergienko, Optical imaging by means of two-photon quantum entanglement, Phys. Rev. A 52, R3429 (1995).

13 N. Picqué and T. W. Hänsch, Frequency comb spectroscopy, Nat. Photonics 13, 146 (2019).

14 I. Coddington, N. Newbury, and W. Swann, Dual-comb spectroscopy, Optica 3, 414 (2016).

15 E. D. Caldwell, L. C. Sinclair, N. R. Newbury, and J.-D. Deschenes, The time-programmable frequency comb and its use in quantum-limited ranging, Nature (London) 610, 667 (2022).

16 M. Takamoto, F.-L. Hong, R. Higashi, and H. Katori, An optical lattice clock, Nature (London) 435, 321 (2005).

17 Z. Jiang, C.-B. Huang, D. E. Leaird, and A. M. Weiner, Optical arbitrary waveform processing of more than 100 spectral comb lines, Nat. Photonics 1, 463 (2007).

18 B. Xu, Z. Chen, T. W. Hänsch, and N. Picqué, Near-ultraviolet photon-counting dual-comb spectroscopy, Nature (London) 627, 289 (2024).

19 M. Walsh, P. Chang, F. Emaury, G. Rieker, N. Newbury, F. Giorgetta, S. Diddams, and J. Genest, Mode-resolved, shot noise limited, dual-comb spectroscopy with independent free running lasers, in Fourier Transform Spectroscopy (Optica Publishing Group, Munich, Germany, 2023), pp. JTh1A--1.

20 S. Camenzind, B. Sierro, B. Willenberg, A. Nussbaum-Lapping, A. Rampur, U. Keller, A. Heidt, and C. R. Phillips, Shot-noise limited dual-comb supercontinuum, Opt. Open 112418 (2024).

21 M. Tse, H. Yu, N. Kijbunchoo, A. Fernandez-Galiana, P. Dupej, L. Barsotti, C. Blair, D. Brown, S. Dwyer, A. Effler et al., Quantum-enhanced Advanced LIGO detectors in the era of gravitational-wave astronomy, Phys. Rev. Lett. 123, 231107 (2019).

22 Y. Xia, W. Li, Q. Zhuang, and Z. Zhang, Quantum-enhanced data classification with a variational entangled sensor network, Phys. Rev. X 11, 021047 (2021).

23 Y. Xia, A. R. Agrawal, C. M. Pluchar, A. J. Brady, Z. Liu, Q. Zhuang, D. J. Wilson, and Z. Zhang, Entanglement-enhanced optomechanical sensing, Nat. Photonics 17, 470 (2023).

24 Z. Zhang, S. Mouradian, F. N. C. Wong, and J. H. Shapiro, Entanglement-enhanced sensing in a lossy and noisy environment, Phys. Rev. Lett. 114, 110506 (2015).

25 A. Belsley, Quantum-enhanced absorption spectroscopy with bright squeezed frequency combs, Phys. Rev. Lett. 130, 133602 (2023).

26 H. Shi, Z. Chen, S. E. Fraser, M. Yu, Z. Zhang, and Q. Zhuang, Entanglement-enhanced dual-comb spectroscopy, npj Quantum Inf. 9, 91 (2023).

27 D. I. Herman, M. Walsh, M. K. Kreider, N. Lordi, E. J. Tsao, A. J. Lind, M. Heyrich, J. Combes, J. Genest, and S. A. Diddams, Squeezed dual-comb spectroscopy, Science 387, 653 (2025).

28 V. Giovannetti, S. Lloyd, and L. Maccone, Advances in quantum metrology, Nat. Photonics 5, 222 (2011).

29 S. Steinlechner, J. Bauchrowitz, M. Meinders, H. Müller-Ebhardt, K. Danzmann, and R. Schnabel, Quantum-dense metrology, Nat. Photonics 7, 626 (2013).

30 M. Chen, N. C. Menicucci, and O. Pfister, Experimental realization of multipartite entanglement of 60 modes of a quantum optical frequency comb, Phys. Rev. Lett. 112, 120505 (2014).

31 D. Walls and G. Milburn, Quantum Optics 2nd Edition, St Lucia, Brisbane QLD (Springer, 2011), 4072.

32 D. I. Herman, M. K. Kreider, N. Lordi, M. Walsh, E. J. Tsao, A. J. Lind, M. Heyrich, J. Combes, S. A. Diddams, and J. Genest, Phase-dependent squeezing in dual-comb interferometry, arXiv:2506.18698.

33 I. E. Gordon, L. S. Rothman, e. R. Hargreaves, R. Hashemi, E. V. Karlovets, F. Skinner, E. K. Conway, C. Hill, R. V. Kochanov, Y. Tan et al., The HITRAN2020 molecular spectroscopic database, J. Quant. Spectrosc. Radiat. Transfer 277, 107949 (2022).

34 A. Parriaux, K. Hammani, and G. Millot, Electro-optic frequency combs Adv. Opt. Photonics 12, 223 (2020).

35 X. Jia, C. Zhai, X. Zhu, C. You, Y. Cao, X. Zhang, Y. Zheng, Z. Fu, J. Mao, T. Dai et al., Continuous-variable multipartite entanglement in an integrated microcomb, Nature (London) 639, 329 (2025).

36 Y. Shen, P.-Y. Hsieh, S. K. Sridhar, S. Feldman, Y.-C. Chang, T. A. Smith, and A. Dutt, Strong nanophotonic quantum squeezing exceeding 3.5 dB in a foundry-compatible Kerr microresonator, Optica 12, 302 (2025).

37 Z. Wang, K. Li, Y. Wang, X. Zhou, Y. Cheng, B. Jing, F. Sun, J. Li, Z. Li, B. Wu et al., Large-scale cluster quantum microcombs, Light Sci. Appl. 14, 164 (2025).

38 Y. Zhang, M. Menotti, K. Tan, V. Vaidya, D. Mahler, L. Helt, L. Zatti, M. Liscidini, B. Morrison, and Z. Vernon, Squeezed light from a nanophotonic molecule, Nat. Commun. 12, 2233 (2021).

39 S. Liu, A. Hariri, B.-H. Wu, Y. Zhang, and Z. Zhang, Generation of squeezed light in silicon nitride photonic integrated chips, in CLEO: Fundamental Science (Optica Publishing Group, 2024), pp. FF2H--6.

40 M. Jahanbozorgi, Z. Yang, S. Sun, H. Chen, R. Liu, B. Wang, and X. Yi, Generation of squeezed quantum microcombs with silicon nitride integrated photonic circuits, Optica 10, 1100 (2023).

41 H. Vahlbruch, M. Mehmet, K. Danzmann, and R. Schnabel, Detection of 15 dB squeezed states of light and their application for the absolute calibration of photoelectric quantum efficiency, Phys. Rev. Lett. 117, 110801 (2016).

42 E. Lucas, S.-P. Yu, T. C. Briles, D. R. Carlson, and S. B. Papp, Tailoring microcombs with inverse-designed, metadispersion microresonators, Nat. Photonics 17, 943 (2023).

43 S.-P. Yu, D. C. Cole, H. Jung, G. T. Moille, K. Srinivasan, and S. B. Papp, Spontaneous pulse formation in edgeless photonic crystal resonators, Nat. Photonics 15, 461 (2021).

44 R. Moreira, S. Gundavarapu, and D. J. Blumenthal, Programmable eye-opener lattice filter for multi-channel dispersion compensation using an integrated compact low-loss silicon nitride platform, Opt. Express 24, 16732 (2016).

45 A. Dutt, C. Joshi, X. Ji, J. Cardenas, Y. Okawachi, K. Luke, A. L. Gaeta, and M. Lipson, On-chip dual-comb source for spectroscopy, Sci. Adv. 4, e1701858 (2018).

46 G. Millot, S. Pitois, M. Yan, T. Hovhannisyan, A. Bendahmane, T. W. Hänsch, and N. Picqué, Frequency-agile dual-comb spectroscopy, Nat. Photonics 10, 27 (2016).

47 E. Deriushkina, I. Rebolledo-Salgado, M. Mazur, V. Torres-Company, P. Andrekson, J. Schröder, and M. Karlsson, Dual-comb swept-wavelength interferometry: Theory and experiment, J. Lightwave Technol. 40, 6508 (2022).

48 V. Durán, P. A. Andrekson, and V. Torres-Company, Electro-optic dual-comb interferometry over 40 nm bandwidth, Opt. Lett. 41, 4190 (2016).

49 A. S. Kowligy, D. R. Carlson, D. D. Hickstein, H. Timmers, A. J. Lind, P. G. Schunemann, S. B. Papp, and S. A. Diddams, Mid-infrared frequency combs at 10 GHz, Opt. Lett. 45, 3677 (2020).

50 M. Yan, Z. Wan, Y. Chen, X. Zhang, and H. Zeng, Quantum correlation-enhanced dual-comb spectroscopy, Light Sci. Appl. 14, 257 (2025).

51 T. Ralph, Can signal-to-noise be improved by heterodyne detection using an amplitude squeezed local oscillator?, Phys. Rev. Lett. 85, 677 (2000).

52 H. Shi et al. (to be published).