基于A* 算法的无人机三维路径规划：MATLAB实现之旅

基于A* 算法的无人机三维路径规划算法，MATLAB编程实现。

在无人机应用日益广泛的今天，高效的路径规划算法至关重要。A算法凭借其在寻找最优路径方面的出色表现，成为众多路径规划场景中的热门选择。本文就来聊聊基于A 算法的无人机三维路径规划，并用MATLAB实现这一过程。

A* 算法简介

A* 算法是一种启发式搜索算法，它结合了Dijkstra算法的广度优先搜索策略和贪心算法的最佳优先搜索策略。其核心在于通过一个估值函数 $f(n) = g(n) + h(n)$ 来评估每个节点的优先级。其中， $g(n)$ 是从起点到节点 $n$ 的实际代价， $h(n)$ 是从节点 $n$ 到目标点的估计代价。

MATLAB 实现代码与分析

初始化环境

matlab 复制代码

% 定义三维空间的大小
x_size = 100;
y_size = 100;
z_size = 50;
% 创建一个三维数组来表示空间，0表示可通行，1表示障碍物
grid = zeros(x_size, y_size, z_size);
% 随机设置一些障碍物
obstacle_ratio = 0.2;
num_obstacles = round(x_size * y_size * z_size * obstacle_ratio);
for i = 1:num_obstacles
    x = randi(x_size);
    y = randi(y_size);
    z = randi(z_size);
    grid(x, y, z) = 1;
end
% 起点和终点
start = [1, 1, 1];
goal = [x_size, y_size, z_size];

在这段代码中，我们首先定义了三维空间的大小，然后创建了一个三维数组 grid 来模拟无人机飞行的空间，其中0表示该位置可通行，1表示存在障碍物。接着通过设定障碍物比例，随机生成了一些障碍物分布在空间中。最后，明确了起点 start 和终点 goal 的位置。

定义启发函数

matlab 复制代码

function h = heuristic(a, b)
    % 使用曼哈顿距离作为启发函数
    h = sum(abs(a - b));
end

这个函数 heuristic 用于计算从一个点 a 到目标点 b 的估计代价，这里采用曼哈顿距离作为启发函数。曼哈顿距离在三维空间中，就是三个维度坐标差值绝对值的和，简单且有效地估计了点与点之间的距离。

A* 搜索主函数

matlab 复制代码

function path = astar_search(grid, start, goal)
    openSet = [];
    openSet(1, :) = start;
    cameFrom = [];
    gScore = inf(size(grid));
    gScore(start(1), start(2), start(3)) = 0;
    fScore = inf(size(grid));
    fScore(start(1), start(2), start(3)) = heuristic(start, goal);

    while ~isempty(openSet)
        [~, current_index] = min(fScore(sub2ind(size(grid), openSet(:, 1), openSet(:, 2), openSet(:, 3))));
        current = openSet(current_index, :);
        if all(current == goal)
            % 找到路径，回溯
            path = [];
            while ~isempty(cameFrom)
                path = [current; path];
                current = cameFrom(end, :);
                cameFrom(end, :) = [];
            end
            path = [start; path; goal];
            return
        end
        openSet(current_index, :) = [];
        neighbors = get_neighbors(current, grid);
        for i = 1:size(neighbors, 1)
            neighbor = neighbors(i, :);
            tentative_gScore = gScore(current(1), current(2), current(3)) + 1;
            if tentative_gScore < gScore(neighbor(1), neighbor(2), neighbor(3))
                cameFrom = [cameFrom; current];
                gScore(neighbor(1), neighbor(2), neighbor(3)) = tentative_gScore;
                fScore(neighbor(1), neighbor(2), neighbor(3)) = tentative_gScore + heuristic(neighbor, goal);
                if ~any(openSet(:, 1) == neighbor(1) & openSet(:, 2) == neighbor(2) & openSet(:, 3) == neighbor(3))
                    openSet = [openSet; neighbor];
                end
            end
        end
    end
    % 如果没有找到路径
    path = [];
end

这个主函数 astar_search 实现了A* 搜索的核心逻辑。首先初始化了开放集合 openSet，用于存储待探索的节点；cameFrom 用于记录每个节点是从哪个节点过来的，方便最后回溯路径；gScore 记录从起点到每个节点的实际代价，初始化为无穷大，起点的 gScore 为0；fScore 记录每个节点的估值，起点的 fScore 为其启发函数值。

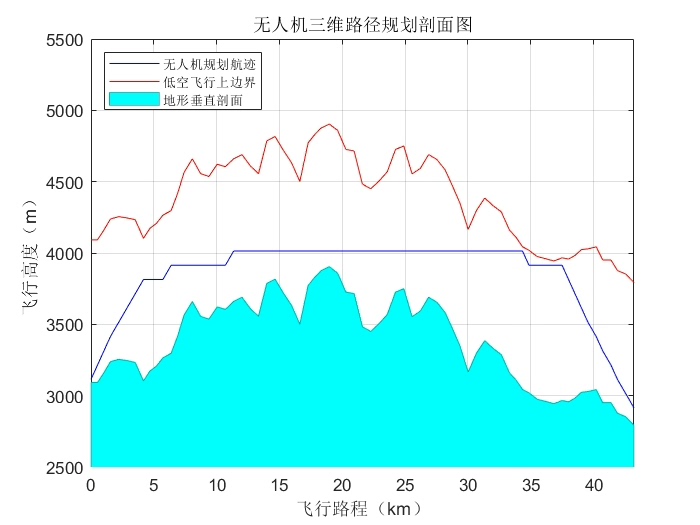
基于A* 算法的无人机三维路径规划算法，MATLAB编程实现。

在 while 循环中，不断从开放集合中选取 fScore 最小的节点 current 进行探索。如果 current 就是目标节点，那么通过回溯 cameFrom 构建出完整的路径。接着获取 current 的邻居节点，计算从起点到邻居节点的暂定 gScore，如果这个值小于邻居节点当前的 gScore，则更新邻居节点的相关信息，并将其加入开放集合。如果循环结束都没有找到目标节点，则返回空路径。

获取邻居节点函数

matlab 复制代码

function neighbors = get_neighbors(node, grid)
    x = node(1);
    y = node(2);
    z = node(3);
    neighbors = [];
    for dx = -1:1
        for dy = -1:1
            for dz = -1:1
                new_x = x + dx;
                new_y = y + dy;
                new_z = z + dz;
                if new_x >= 1 && new_x <= size(grid, 1) && new_y >= 1 && new_y <= size(grid, 2) && new_z >= 1 && new_z <= size(grid, 3) && grid(new_x, new_y, new_z) == 0
                    neighbors = [neighbors; new_x, new_y, new_z];
                end
            end
        end
    end
end

get_neighbors 函数用于获取给定节点在三维空间中的邻居节点。通过三层循环遍历节点周围的所有可能位置，检查这些位置是否在空间范围内且没有障碍物，如果满足条件则将其作为邻居节点加入 neighbors 数组中。

调用与显示

matlab 复制代码

path = astar_search(grid, start, goal);
if ~isempty(path)
    figure;
    hold on;
    % 绘制障碍物
    [X, Y, Z] = ind2sub(size(grid), find(grid == 1));
    scatter3(X, Y, Z, 'filled', 'r');
    % 绘制路径
    plot3(path(:, 1), path(:, 2), path(:, 3), 'b - o');
    xlabel('X');
    ylabel('Y');
    zlabel('Z');
    title('无人机三维路径规划');
else
    disp('没有找到可行路径');
end

最后，调用 astar_search 函数获取路径，如果找到路径，使用MATLAB的绘图函数 scatter3 和 plot3 分别绘制出障碍物和路径，直观展示无人机的规划路径；如果没有找到路径，则提示相应信息。

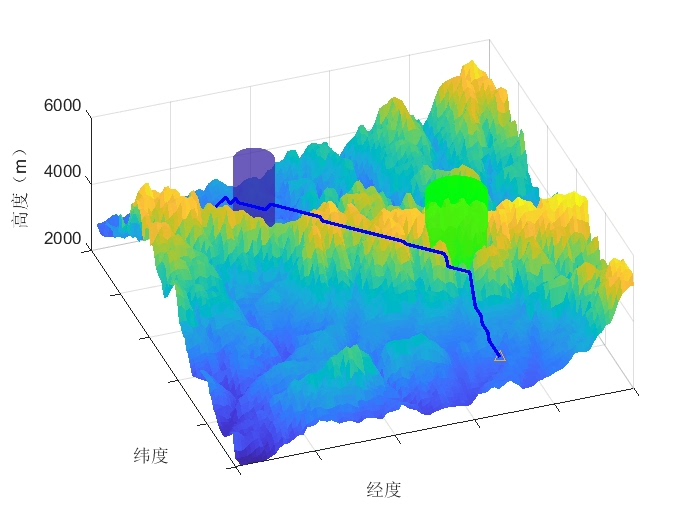
通过以上MATLAB代码实现，我们成功地基于A* 算法完成了无人机的三维路径规划，为无人机在复杂三维环境中的自主飞行提供了有效的路径规划方案。当然，实际应用中可能还需要考虑更多的因素，比如动态障碍物、飞行约束等，但这为进一步的研究和改进奠定了基础。