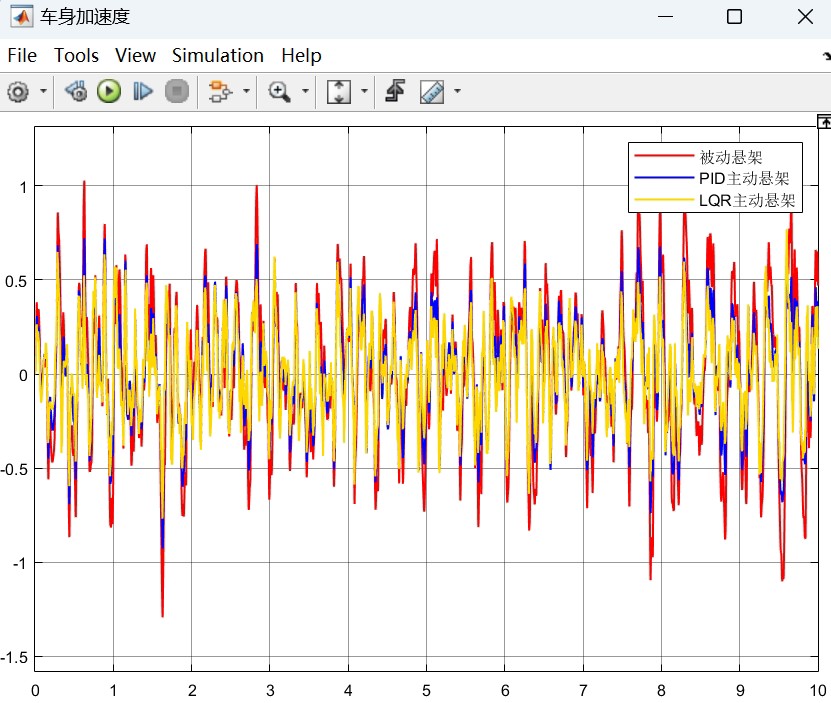
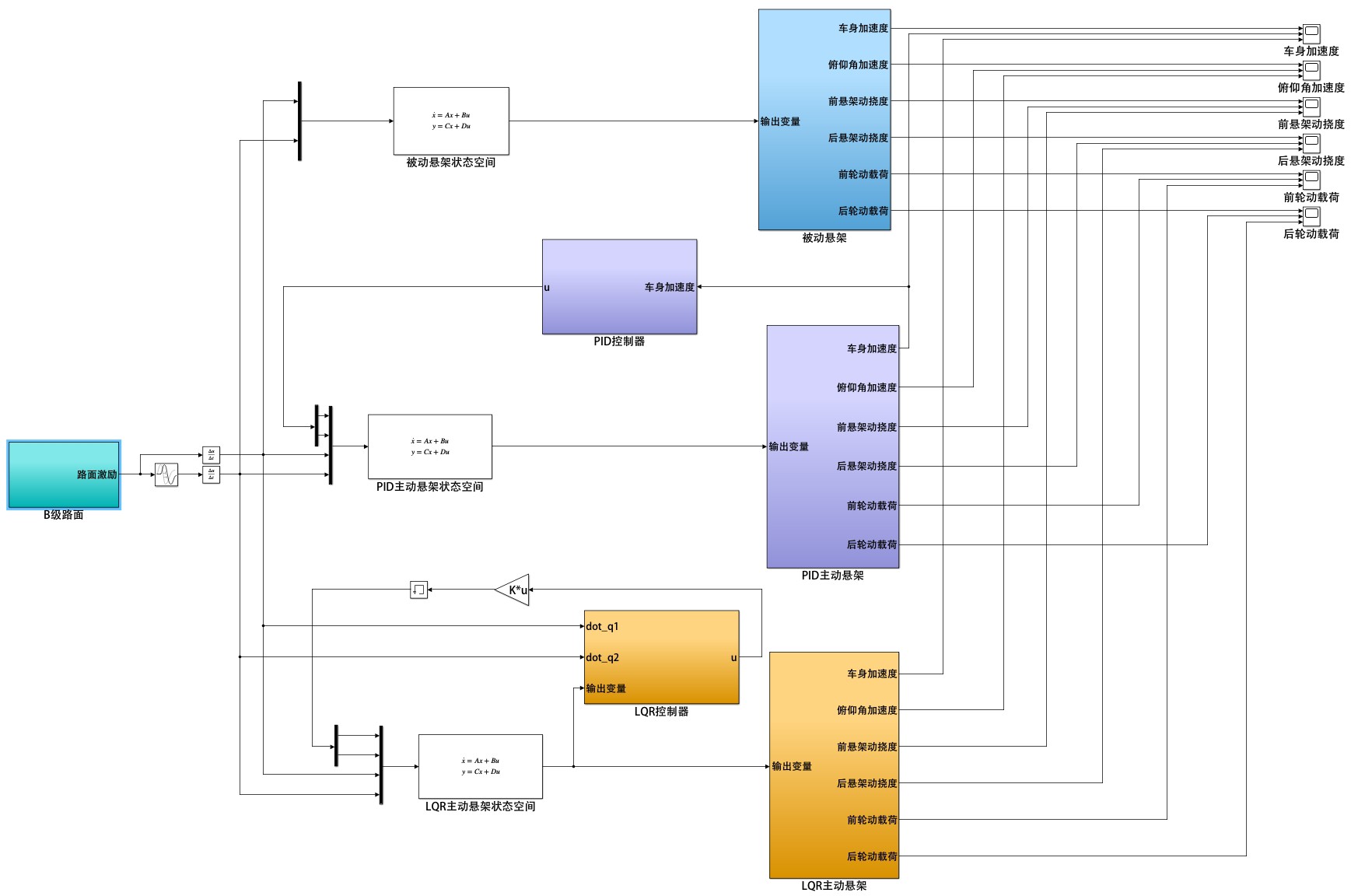
【PID和LQR主动悬架模型对比】 分别建立了PID控制和LQR控制的的主动悬架模型,比较两种控制器的控制效果。 以悬架主动力为控制目标,输入为B级随机路面,输出为车身垂向加速度、俯仰角加速度、悬架动挠度等平顺性评价指标,可做汽车平顺性仿真。 二自由度(1/4)车辆模型:r360. 四自由度(1/2)车辆模型:r550. 内容包括模型所有源文件,说明文档和参考资料
在汽车工程领域,提升车辆的平顺性一直是重要的研究方向。主动悬架系统作为关键技术,能够显著改善车辆在行驶过程中的舒适性和稳定性。今天咱们就来对比一下 PID 控制和 LQR 控制的主动悬架模型,看看它们在汽车平顺性仿真中的表现。
模型建立基础
我们使用了两种经典的车辆模型:二自由度(1/4)车辆模型(r360)和四自由度(1/2)车辆模型(r550)。1/4 车辆模型相对简单,主要考虑车身垂直方向运动和悬架的压缩伸张,能快速对悬架控制效果进行初步评估。1/2 车辆模型则更为复杂,除了车身垂直运动,还考虑了俯仰角运动,更贴近实际车辆行驶状况。
PID 控制主动悬架模型
PID 控制器是一种经典的反馈控制器,它根据设定值与实际输出值的偏差,通过比例(P)、积分(I)、微分(D)三个环节的线性组合来调整控制量。
以下是一段简单的 Python 实现 PID 控制的代码示例(假设这里简化了车辆模型参数等复杂情况,仅突出 PID 控制逻辑):
python
class PIDController:
def __init__(self, kp, ki, kd):
self.kp = kp
self.ki = ki
self.kd = kd
self.prev_error = 0
self.integral = 0
def update(self, setpoint, process_variable):
error = setpoint - process_variable
self.integral += error
derivative = error - self.prev_error
control_signal = self.kp * error + self.ki * self.integral + self.kd * derivative
self.prev_error = error
return control_signal在这个代码中,init 方法初始化了 PID 控制器的三个参数 kp(比例系数)、ki(积分系数)、kd(微分系数),并初始化了一些用于计算的变量。update 方法则根据当前的设定值(setpoint)和实际输出值(process_variable)计算出控制信号。比例环节 kp error**能快速响应偏差,积分环节 ki integral 用于消除稳态误差,微分环节 kd * derivative 能预测偏差变化趋势提前调整。
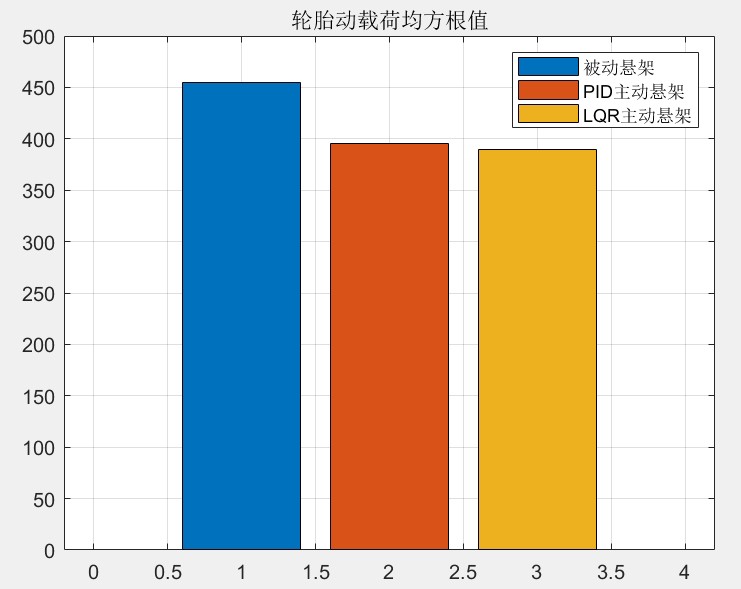
在主动悬架模型里,我们以悬架主动力为控制目标,输入 B 级随机路面激励,PID 控制器根据车身垂向加速度、俯仰角加速度、悬架动挠度等平顺性评价指标的偏差,不断调整悬架主动力,来改善车辆平顺性。
LQR 控制主动悬架模型
LQR(线性二次型调节器)是一种基于状态空间的最优控制方法,它通过最小化一个二次型性能指标来确定最优控制律。相比 PID,LQR 考虑了系统的整体状态,能得到理论上的最优控制效果。
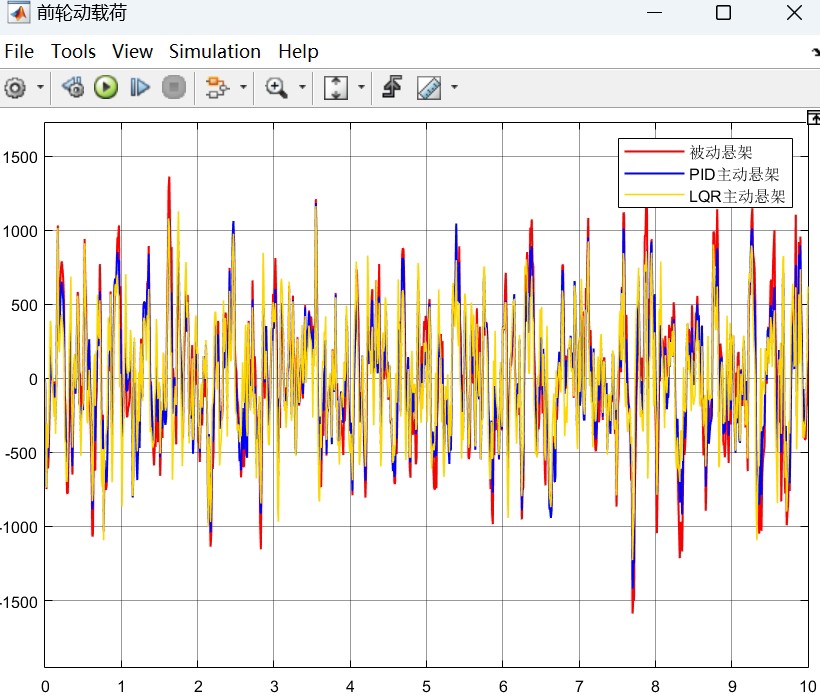
【PID和LQR主动悬架模型对比】 分别建立了PID控制和LQR控制的的主动悬架模型,比较两种控制器的控制效果。 以悬架主动力为控制目标,输入为B级随机路面,输出为车身垂向加速度、俯仰角加速度、悬架动挠度等平顺性评价指标,可做汽车平顺性仿真。 二自由度(1/4)车辆模型:r360. 四自由度(1/2)车辆模型:r550. 内容包括模型所有源文件,说明文档和参考资料
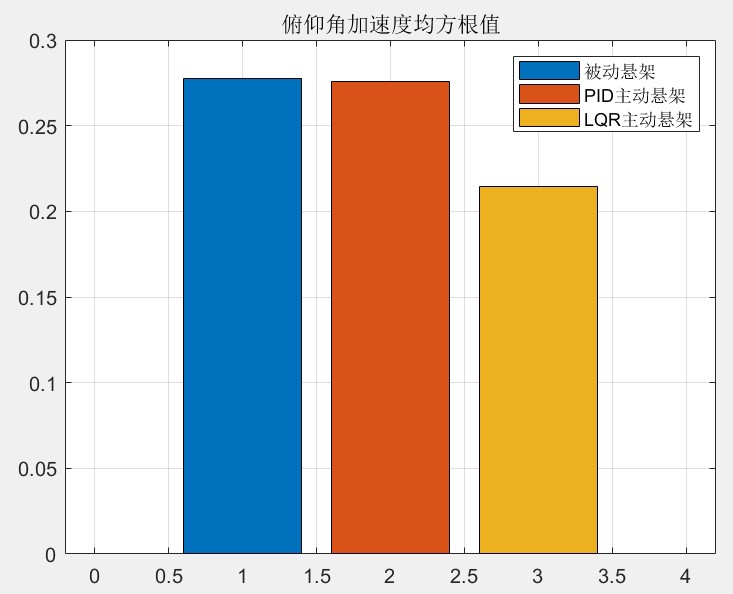
下面是一个简单的基于线性系统的 LQR 控制 Python 代码示例(同样简化处理,仅展示核心逻辑):
python
import numpy as np
from scipy.linalg import solve_continuous_are
def lqr(A, B, Q, R):
# 求解代数 Riccati 方程
P = solve_continuous_are(A, B, Q, R)
K = np.dot(np.linalg.inv(R), np.dot(B.T, P))
return K这里的 A 是系统矩阵,描述了系统状态的变化;B 是输入矩阵,确定了控制输入如何影响系统状态;Q 是状态加权矩阵,用于权衡不同状态变量对性能指标的影响;R 是控制加权矩阵,体现对控制输入大小的限制。通过求解代数 Riccati 方程得到矩阵 P,进而计算出最优反馈增益矩阵 K。在主动悬架模型中,根据车辆状态和这些矩阵计算出最优的悬架主动力控制量。
控制效果比较与分析
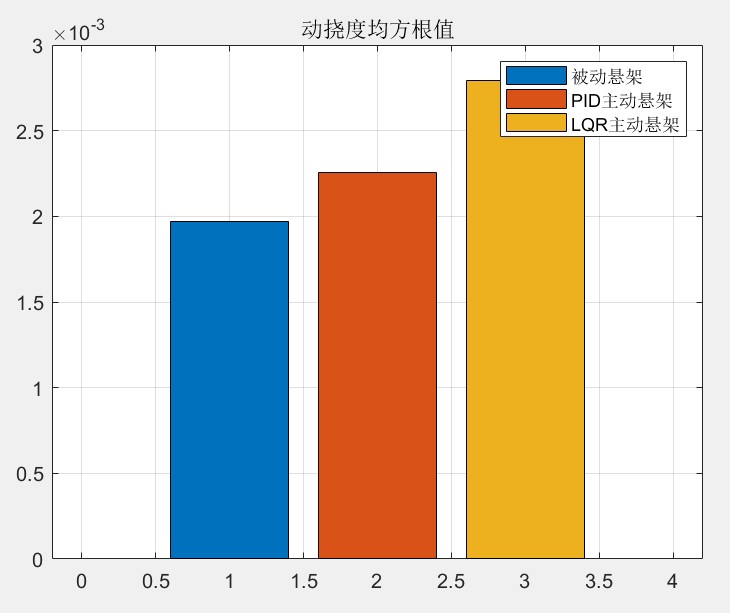
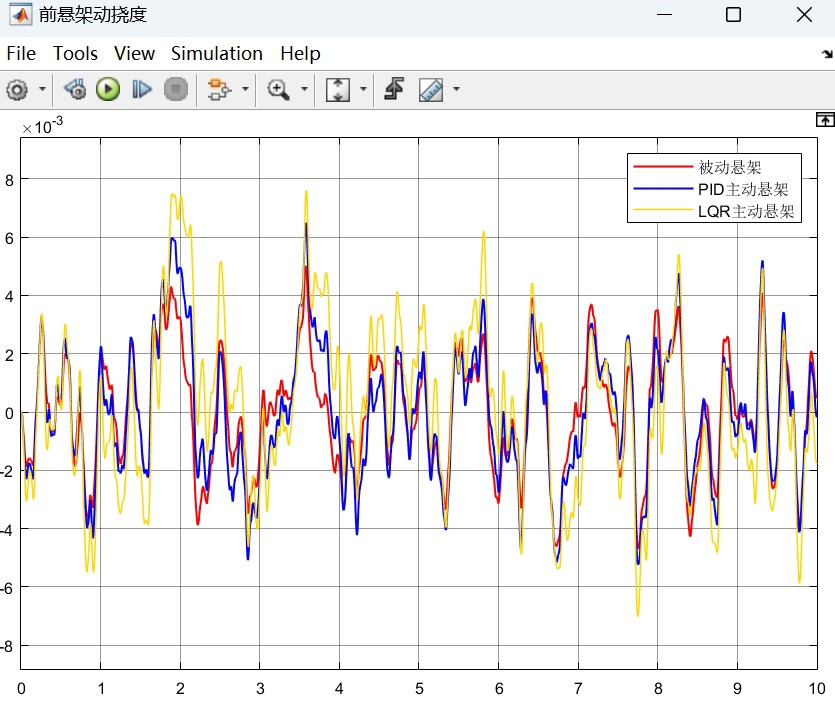
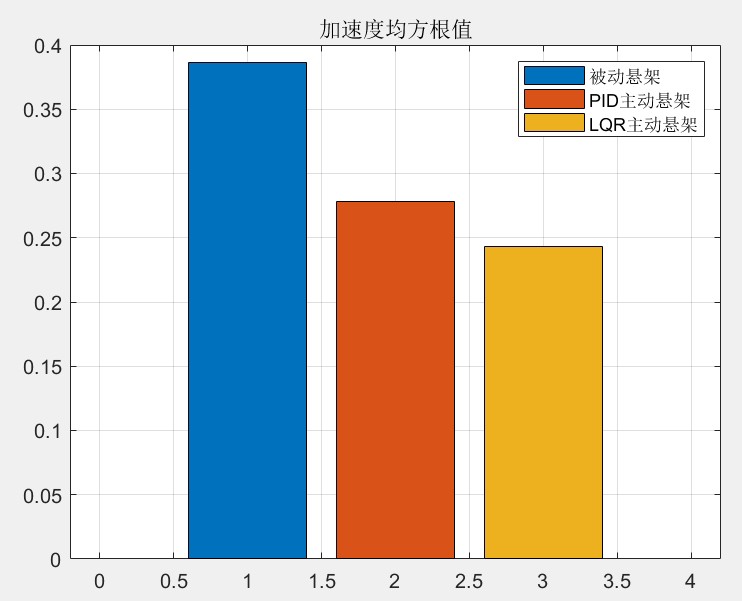
在汽车平顺性仿真中,以 B 级随机路面为输入,对比两种控制器的输出结果,即车身垂向加速度、俯仰角加速度、悬架动挠度等平顺性评价指标。PID 控制器结构简单,易于实现和调试,对于一些不太复杂的工况能有不错的控制效果。但它依赖于经验和试错来调整参数,面对复杂多变的路面情况和车辆动态特性,可能无法达到最优控制。
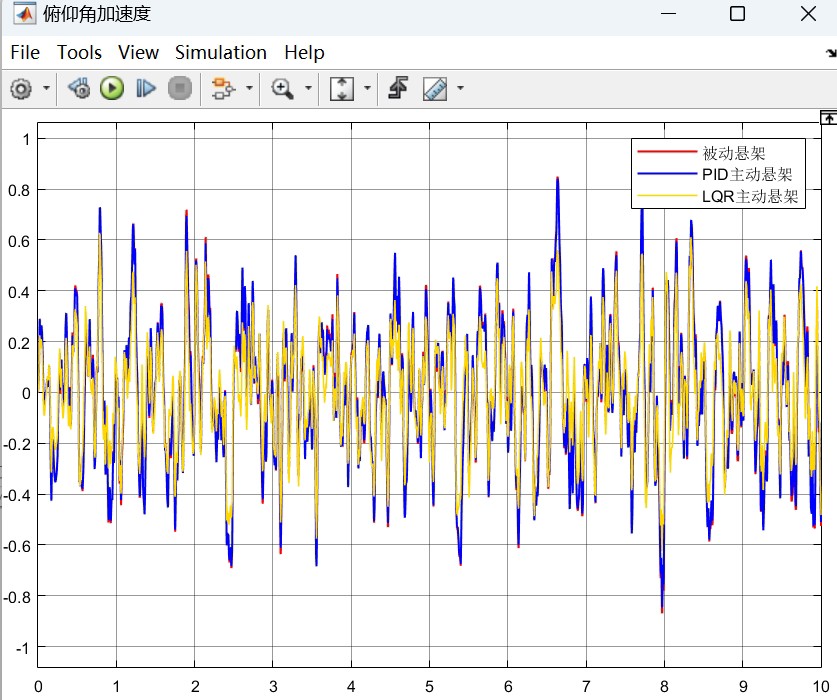
而 LQR 控制器基于系统的状态空间模型,理论上能找到全局最优解,对车辆整体状态的把控更好,在复杂工况下能更有效地提升车辆平顺性。不过,LQR 控制器的设计依赖于精确的系统模型,实际应用中车辆模型参数可能存在不确定性,这对其控制效果会有一定影响。
这次研究提供了模型所有源文件、说明文档和参考资料,感兴趣的小伙伴可以深入研究和实践,看看如何进一步优化主动悬架系统,提升汽车的平顺性。无论是 PID 这种经典老将,还是 LQR 这种基于现代控制理论的新秀,都在为汽车行驶的舒适性和稳定性贡献着力量。希望未来能看到更多基于这些技术的创新,让我们的出行更加舒适平稳。