目录
[第一代:经典统计时序模型(时间 = 线性相关)](#第一代:经典统计时序模型(时间 = 线性相关))
[一、AR 模型:用"过去的自己"预测现在](#一、AR 模型:用“过去的自己”预测现在)
[1️⃣ AR 模型的思想](#1️⃣ AR 模型的思想)
[AR(p) 的数学定义](#AR(p) 的数学定义)
[2️⃣ AR 模型在"学"什么?](#2️⃣ AR 模型在“学”什么?)
[3️⃣ AR 的隐含限制(关键)](#3️⃣ AR 的隐含限制(关键))
[二、MA 模型:不是过去的值,而是过去的"冲击"](#二、MA 模型:不是过去的值,而是过去的“冲击”)
[1️⃣ MA 模型的动机](#1️⃣ MA 模型的动机)
[2️⃣ MA(q) 的数学定义](#2️⃣ MA(q) 的数学定义)
[3️⃣ AR vs MA 的本质区别(非常重要)](#3️⃣ AR vs MA 的本质区别(非常重要))
[4️⃣ MA 的致命问题](#4️⃣ MA 的致命问题)
[1️⃣ 为什么 AR 和 MA 必须合体?](#1️⃣ 为什么 AR 和 MA 必须合体?)
[2️⃣ ARMA(p, q) 的数学形式](#2️⃣ ARMA(p, q) 的数学形式)
[3️⃣ 一个非常重要但常被忽略的事实](#3️⃣ 一个非常重要但常被忽略的事实)
[🔥 关键转折问题](#🔥 关键转折问题)
时间序列到底在建模什么?
一个根本问题
如果我今天看到一个数 yt,
我凭什么认为它和昨天 yt−1有关系?
时间序列建模的最原始假设只有一句话:
时间上相邻的观测值不是独立的
第一代:经典统计时序模型(时间 = 线性相关)
代表模型
-
AR / MA / ARMA
-
ARIMA / SARIMA
-
Holt / Holt-Winters
-
State Space Models
时间序列的最小假设(第一代模型的世界观)
第一代模型默认三个前提:
-
时间是单向的(过去 → 现在 → 未来)
-
依赖是线性的
-
统计性质不随时间改变(平稳性)
👉 所有经典模型,都是在这三条假设里打转。
一、AR 模型:用"过去的自己"预测现在
AR 模型(Autoregressive Model),即自回归模型。
引出问题
假设我问你:
明天的气温,会不会和昨天、前天有关?
你会说:
当然会,而且可能主要跟最近几天有关。
这就是 AR(Autoregressive)的直觉来源。
1️⃣ AR 模型的思想
核心假设:
当前值是过去若干个值的线性组合 + 噪声
AR(p) 的数学定义
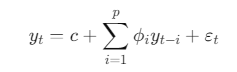
我们逐项"翻译成人话":
-
yt:当前时刻的观测
-
yt−i:过去第 i个时刻
-
ϕi:时间依赖的强度
-
εt:白噪声(不可预测部分)
-
p:记忆长度
📌 时间在这里是什么?
时间 = 有限阶滞后(finite lag)
2️⃣ AR 模型在"学"什么?
它本质在学一组参数:
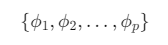
你可以理解为:
"过去第 1 天重要吗?第 2 天重要吗?第 7 天还有影响吗?"
3️⃣ AR 的隐含限制(关键)
现在我们问一个非常重要的问题:
如果真实世界是这样生成的:
系统本身没"惯性"
但噪声会持续影响好几天
AR 能处理吗?
答案是:不太行。
因为 AR 只把"记忆"放在 y 上 ,
但没记住噪声。
二、MA 模型:不是过去的值,而是过去的"冲击"
MA模型(Moving Average Model),即移动平均/滑动平均模型。
1️⃣ MA 模型的动机
换个角度想:
现在的值,可能并不是过去状态决定的
而是过去一些"随机事件"的残留效应
比如:
-
一次政策冲击
-
一次设备误差
-
一次心理应激
2️⃣ MA(q) 的数学定义
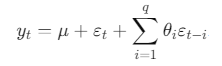
逐项解释:
-
μ:时间序列的均值或期望值,这个值对所有的时间点都是相同的。
-
εt:当前冲击
-
εt−i:过去的冲击
-
θi:冲击的"衰减方式"
📌 时间在这里是什么?
时间 = 冲击的持续影响
3️⃣ AR vs MA 的本质区别(非常重要)
| 模型 | 记忆的对象 |
|---|---|
| AR | 过去的值 |
| MA | 过去的噪声 |
你可以这样理解:
-
AR:系统有"惯性"
-
MA:系统被"外力"反复敲击
4️⃣ MA 的致命问题
你现在应该能隐约感觉到:
MA 模型需要知道 εt−1
但问题是:
噪声是不可观测的
这就带来一个现实问题:
-
MA 在理论上优美
-
在实践中难以直接解释
三、ARMA:世界不是非黑即白
自回归滑动平均模型,又名ARMA模型(Auto-Regressive Moving Average Model),由自回归模型(AR模型)与滑动平均模型(MA模型)为基础"混合"而成。
1️⃣ 为什么 AR 和 MA 必须合体?
因为现实系统往往同时满足:
-
有内在惯性(AR)
-
又不断受到随机冲击(MA)
👉 只用一个视角都不完整
2️⃣ ARMA(p, q) 的数学形式
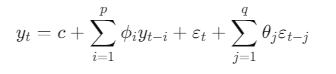
你现在可以把它理解为:
当前 = 过去状态的残留 + 过去冲击的残留
3️⃣ 一个非常重要但常被忽略的事实
ARMA 只能用于平稳时间序列
也就是说:
-
均值不随时间变
-
方差不随时间变
-
自相关结构稳定
👉 你现在可以问一个致命问题了。
🔥 关键转折问题
请你认真想这个问题:
如果时间序列本身在"走趋势"
比如情绪评分、GDP、气温、学习进展
AR / MA / ARMA 还能直接用吗?
答案是:不能。
这正是 ARIMA 出现的历史必然性。
下一讲: