从零开始学AI9——机器学习2

Godspeed Zhao2026-02-10 17:02
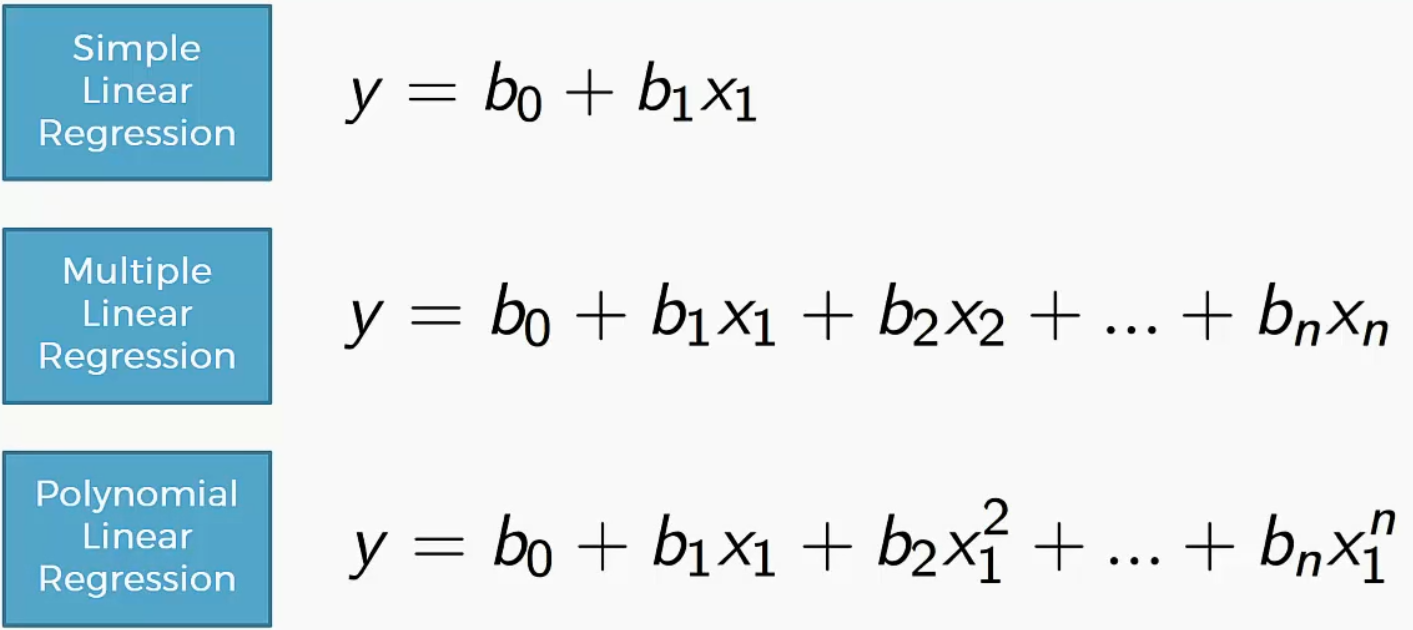
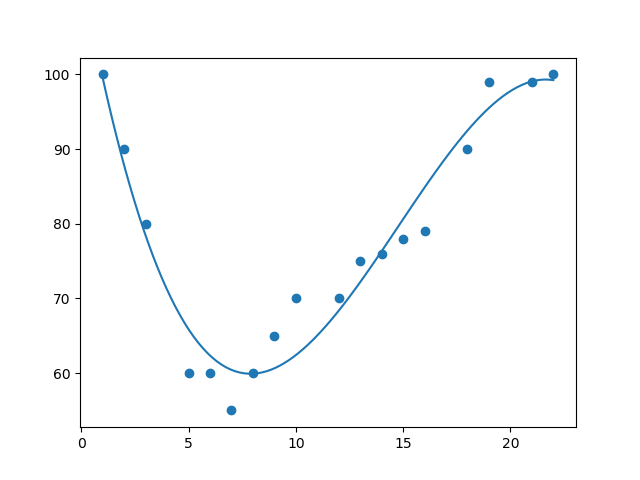
  • 多项式回归 (Polynomial Regression):
    • 原理： 直线拟合不了，就用曲线（二次方、三次方）去拟合。

多项式回归 (Polynomial Regression) 基础数学推导

1. 为什么需要多项式回归？

线性回归假设特征与目标之间是线性关系：

y=θ0+θ1x

但现实中很多关系是非线性的，例如：

  • 房价与面积的关系（边际效应递减）
  • 物体运动轨迹（抛物线）
  • 人口增长曲线

2. 多项式回归的核心思想

2.1 模型表示

关键洞察 ：多项式回归本质上是特征工程 + 线性回归。

对于单变量 xx，我们可以构造多项式特征：

阶数 模型 特征
1次 y=θ0+θ1xy=θ0​+θ1​x [1,x][1,x]
2次 y=θ0+θ1x+θ2x2y=θ0​+θ1​x+θ2​x2 [1,x,x2][1,x,x2]
3次 y=θ0+θ1x+θ2x2+θ3x3y=θ0​+θ1​x+θ2​x2+θ3​x3 [1,x,x2,x3][1,x,x2,x3]
n次 y=∑j=0nθjxjy=∑j=0n​θj​xj [1,x,x2,...,xn][1,x,x2,...,xn]

2.2 变量替换

令：

z0=1,z1=x,z2=x2,...,zn=xnz0​=1,z1​=x,z2​=x2,...,zn​=xn

则多项式回归变为：

y=θ0z0+θ1z1+θ2z2+...+θnzn=θTzy=θ0​z0​+θ1​z1​+θ2​z2​+...+θn​zn​=θTz

这就是标准的线性回归形式！ 只不过特征从 xx 变成了 [1,x,x2,...,xn][1,x,x2,...,xn]。

3. 数学推导

3.1 问题设定

给定 mm 个样本 {(x(i),y(i))}i=1m{(x(i),y(i))}i=1m​，使用 nn 次多项式拟合。

特征矩阵构造（Vandermonde 矩阵）：

X=(1x(1)(x(1))2⋯(x(1))n1x(2)(x(2))2⋯(x(2))n⋮⋮⋮⋱⋮1x(m)(x(m))2⋯(x(m))n)m×(n+1)X=​11⋮1​x(1)x(2)⋮x(m)​(x(1))2(x(2))2⋮(x(m))2​⋯⋯⋱⋯​(x(1))n(x(2))n⋮(x(m))n​​m×(n+1)​

参数向量 ：

θ=[θ0,θ1,θ2,...,θn]Tθ=[θ0​,θ1​,θ2​,...,θn​]T

目标向量 ：

y=[y(1),y(2),...,y(m)]Ty=[y(1),y(2),...,y(m)]T

3.2 代价函数

与线性回归完全相同，使用均方误差：

J(θ)=12m∑i=1m(hθ(x(i))−y(i))2J(θ)=2m1​i=1∑m​(hθ​(x(i))−y(i))2

其中预测函数：

hθ(x)=∑j=0nθjxj=θ0+θ1x+θ2x2+...+θnxnhθ​(x)=∑j=0n​θj​xj=θ0​+θ1​x+θ2​x2+...+θn​xn

矩阵形式：

J(θ)=12m(Xθ−y)T(Xθ−y)J(θ)=2m1​(Xθ−y)T(Xθ−y)

3.3 求解方法

方法一：正规方程

由于形式与线性回归相同，直接套用正规方程：

θ=(XTX)−1XTyθ=(XTX)−1XTy

方法二：梯度下降

梯度计算：

∂J∂θj=1m∑i=1m(hθ(x(i))−y(i))⋅(x(i))j∂θj​∂J​=m1​i=1∑m​(hθ​(x(i))−y(i))⋅(x(i))j

更新规则：

θj:=θj−α1m∑i=1m(hθ(x(i))−y(i))⋅(x(i))jθj​:=θj​−αm1​i=1∑m​(hθ​(x(i))−y(i))⋅(x(i))j

注意 ：由于 xjxj 的尺度差异很大（如 x=100x=100 时，x3=106x3=106），特征缩放非常重要！

4. 多变量多项式回归

4.1 问题扩展

当有多个原始特征 x1,x2,...,xkx1​,x2​,...,xk​ 时，多项式特征包括：

类型 示例（2个特征，2次）
常数项 11
一次项 x1,x2x1​,x2​
二次项 x12,x1x2,x22x12​,x1​x2​,x22​
交叉项 x1x2x1​x2​（特征交互）

2变量2次多项式 ：

y=θ0+θ1x1+θ2x2+θ3x12+θ4x1x2+θ5x22y=θ0​+θ1​x1​+θ2​x2​+θ3​x12​+θ4​x1​x2​+θ5​x22​

4.2 特征数量爆炸

对于 kk 个原始特征，nn 次多项式的特征数量：

特征数=(n+kk)=(n+k)!n!⋅k!特征数=(kn+k​)=n!⋅k!(n+k)!​

原始特征 k 多项式阶数 n 总特征数
2 2 6
2 3 10
5 2 21
5 3 56
10 3 286
10 5 3003

特征数量快速增长，容易导致过拟合！

5. 过拟合与正则化

5.1 过拟合问题

复制代码 
欠拟合 (1次)           恰当拟合 (2次)         过拟合 (15次)
    y                      y                      y
    │    ●                 │   ●                  │  ●╱╲●
    │  ●  ●               │  ●  ●                │ ●    ●
    │●      ●             │●      ●              │●      ●
    │  ────────           │   ⌒⌒⌒               │ ╱╲╱╲╱╲╱
    └──────────x          └──────────x           └──────────x
    
  偏差高，方差低          偏差低，方差低          偏差低，方差高
  训练误差：高            训练误差：适中          训练误差：极低
  测试误差：高            测试误差：低            测试误差：很高

5.2 正则化解决过拟合

在代价函数中添加惩罚项，限制参数大小：

Ridge 回归（L2 正则化） ：

J(θ)=12m∑i=1m(hθ(x(i))−y(i))2+λ∑j=1nθj2J(θ)=2m1​∑i=1m​(hθ​(x(i))−y(i))2+λ∑j=1n​θj2​

正规方程解 ：

θ=(XTX+λI′)−1XTyθ=(XTX+λI′)−1XTy

其中 I′I′ 是单位矩阵，但 (0,0)(0,0) 位置为 0（不惩罚偏置项）。

Lasso 回归（L1 正则化） ：

J(θ)=12m∑i=1m(hθ(x(i))−y(i))2+λ∑j=1n∣θj∣J(θ)=2m1​∑i=1m​(hθ​(x(i))−y(i))2+λ∑j=1n​∣θj​∣

L1 正则化可以产生稀疏解（部分参数为0），起到特征选择的作用。

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.pipeline import Pipeline
from sklearn.model_selection import cross_val_score
from sklearn.metrics import mean_squared_error, r2_score

# ============================================================
# 第一部分：生成非线性数据
# ============================================================
np.random.seed(42)

# 生成数据：y = 0.5x² - 2x + 1 + noise
m = 50
x = np.linspace(-3, 3, m)
y_true = 0.5 * x**2 - 2 * x + 1  # 真实函数
y = y_true + np.random.normal(0, 0.5, m)  # 添加噪声

print("=" * 60)
print("多项式回归演示")
print("=" * 60)
print(f"真实函数: y = 0.5x² - 2x + 1")
print(f"样本数量: {m}")
print(f"数据范围: x ∈ [{x.min():.1f}, {x.max():.1f}]")

# ============================================================
# 第二部分：手动实现多项式回归
# ============================================================
def create_polynomial_features(x, degree):
    """
    手动创建多项式特征矩阵
    
    参数:
        x: 原始特征向量 (m,)
        degree: 多项式阶数
    
    返回:
        X: 多项式特征矩阵 (m, degree+1)
    """
    m = len(x)
    X = np.zeros((m, degree + 1))
    
    for j in range(degree + 1):
        X[:, j] = x ** j  # 第j列是 x^j
    
    return X


def polynomial_regression_normal_equation(x, y, degree):
    """
    使用正规方程求解多项式回归
    """
    # 构建多项式特征矩阵
    X = create_polynomial_features(x, degree)
    
    # 正规方程求解
    theta = np.linalg.inv(X.T @ X) @ X.T @ y
    
    return theta, X


def polynomial_regression_gradient_descent(x, y, degree, alpha=0.01, 
                                            iterations=10000):
    """
    使用梯度下降求解多项式回归（带特征缩放）
    """
    # 构建多项式特征矩阵
    X = create_polynomial_features(x, degree)
    m, n = X.shape
    
    # 特征缩放（非常重要！）
    mu = np.mean(X[:, 1:], axis=0)  # 不缩放第0列（常数1）
    sigma = np.std(X[:, 1:], axis=0)
    sigma[sigma == 0] = 1  # 避免除以0
    
    X_norm = X.copy()
    X_norm[:, 1:] = (X[:, 1:] - mu) / sigma
    
    # 梯度下降
    theta = np.zeros(n)
    cost_history = []
    
    for i in range(iterations):
        predictions = X_norm @ theta
        errors = predictions - y
        gradient = (1/m) * (X_norm.T @ errors)
        theta = theta - alpha * gradient
        cost = (1/(2*m)) * np.sum(errors**2)
        cost_history.append(cost)
    
    # 将参数转换回原始尺度
    theta_original = np.zeros(n)
    theta_original[0] = theta[0] - np.sum(theta[1:] * mu / sigma)
    theta_original[1:] = theta[1:] / sigma
    
    return theta_original, cost_history


# 使用正规方程拟合2次多项式
print("\n" + "-" * 60)
print("手动实现 - 正规方程法（2次多项式）")
print("-" * 60)

theta_2, X_2 = polynomial_regression_normal_equation(x, y, degree=2)

print("拟合结果: y = {:.4f} + {:.4f}x + {:.4f}x²".format(
    theta_2[0], theta_2[1], theta_2[2]))
print("真实参数: y = 1.0000 + (-2.0000)x + 0.5000x²")

# 计算预测和评估
y_pred_2 = X_2 @ theta_2
mse_2 = mean_squared_error(y, y_pred_2)
r2_2 = r2_score(y, y_pred_2)
print(f"MSE: {mse_2:.4f}, R²: {r2_2:.4f}")

# ============================================================
# 第三部分：不同阶数对比（欠拟合 vs 过拟合）
# ============================================================
print("\n" + "-" * 60)
print("不同多项式阶数对比")
print("-" * 60)

degrees = [1, 2, 4, 15]
results = {}

for d in degrees:
    theta, X_poly = polynomial_regression_normal_equation(x, y, d)
    y_pred = X_poly @ theta
    mse = mean_squared_error(y, y_pred)
    r2 = r2_score(y, y_pred)
    results[d] = {'theta': theta, 'mse': mse, 'r2': r2, 'X': X_poly}
    print(f"阶数 {d:2d}: MSE = {mse:.4f}, R² = {r2:.4f}, 参数数量 = {d+1}")

# ============================================================
# 第四部分：sklearn 实现
# ============================================================
print("\n" + "-" * 60)
print("sklearn 实现")
print("-" * 60)

# 方法1：手动步骤
X_reshape = x.reshape(-1, 1)  # sklearn需要2D输入

poly = PolynomialFeatures(degree=2, include_bias=True)
X_poly_sklearn = poly.fit_transform(X_reshape)

model = LinearRegression(fit_intercept=False)  # bias已包含在特征中
model.fit(X_poly_sklearn, y)

print("sklearn PolynomialFeatures + LinearRegression:")
print(f"  系数: {model.coef_}")

# 方法2：使用 Pipeline（推荐）
print("\n使用 Pipeline 简化流程:")

for d in [1, 2, 4]:
    pipeline = Pipeline([
        ('poly', PolynomialFeatures(degree=d)),
        ('linear', LinearRegression())
    ])
    pipeline.fit(X_reshape, y)
    y_pred = pipeline.predict(X_reshape)
    r2 = r2_score(y, y_pred)
    print(f"  阶数 {d}: R² = {r2:.4f}")

# ============================================================
# 第五部分：正则化多项式回归
# ============================================================
print("\n" + "-" * 60)
print("正则化多项式回归（防止过拟合）")
print("-" * 60)

# 使用15次多项式，对比有无正则化
degree = 15

# 无正则化
pipe_normal = Pipeline([
    ('poly', PolynomialFeatures(degree=degree)),
    ('linear', LinearRegression())
])
pipe_normal.fit(X_reshape, y)
y_pred_normal = pipe_normal.predict(X_reshape)

# Ridge 正则化
pipe_ridge = Pipeline([
    ('poly', PolynomialFeatures(degree=degree)),
    ('ridge', Ridge(alpha=0.1))
])
pipe_ridge.fit(X_reshape, y)
y_pred_ridge = pipe_ridge.predict(X_reshape)

# Lasso 正则化
pipe_lasso = Pipeline([
    ('poly', PolynomialFeatures(degree=degree)),
    ('lasso', Lasso(alpha=0.01, max_iter=10000))
])
pipe_lasso.fit(X_reshape, y)
y_pred_lasso = pipe_lasso.predict(X_reshape)

print(f"{'方法':<20} {'训练 R²':<12} {'参数范围':<20}")
print("-" * 52)

# 获取参数范围
coef_normal = pipe_normal.named_steps['linear'].coef_
coef_ridge = pipe_ridge.named_steps['ridge'].coef_
coef_lasso = pipe_lasso.named_steps['lasso'].coef_

print(f"{'无正则化':<20} {r2_score(y, y_pred_normal):<12.4f} "
      f"[{coef_normal.min():.1f}, {coef_normal.max():.1f}]")
print(f"{'Ridge (L2)':<20} {r2_score(y, y_pred_ridge):<12.4f} "
      f"[{coef_ridge.min():.2f}, {coef_ridge.max():.2f}]")
print(f"{'Lasso (L1)':<20} {r2_score(y, y_pred_lasso):<12.4f} "
      f"[{coef_lasso.min():.2f}, {coef_lasso.max():.2f}]")

# 统计Lasso的稀疏性
n_zeros = np.sum(np.abs(coef_lasso) < 1e-6)
print(f"\nLasso 稀疏性: {n_zeros}/{len(coef_lasso)} 个参数接近0")

# ============================================================
# 第六部分：交叉验证选择最佳阶数
# ============================================================
print("\n" + "-" * 60)
print("交叉验证选择最佳多项式阶数")
print("-" * 60)

degrees_to_test = range(1, 16)
cv_scores = []

for d in degrees_to_test:
    pipeline = Pipeline([
        ('poly', PolynomialFeatures(degree=d)),
        ('linear', LinearRegression())
    ])
    # 5折交叉验证，使用负MSE作为评分
    scores = cross_val_score(pipeline, X_reshape, y, 
                            cv=5, scoring='neg_mean_squared_error')
    cv_scores.append(-scores.mean())  # 转为正MSE

best_degree = degrees_to_test[np.argmin(cv_scores)]
print(f"交叉验证结果：")
for d, score in zip(degrees_to_test, cv_scores):
    marker = " <-- 最佳" if d == best_degree else ""
    print(f"  阶数 {d:2d}: CV-MSE = {score:.4f}{marker}")

# ============================================================
# 第七部分：可视化
# ============================================================
fig, axes = plt.subplots(2, 3, figsize=(15, 10))

# 图1-4: 不同阶数的拟合效果
x_plot = np.linspace(-3.5, 3.5, 200)

for idx, d in enumerate([1, 2, 4, 15]):
    ax = axes[idx // 2, idx % 2]
    
    # 训练模型
    pipe = Pipeline([
        ('poly', PolynomialFeatures(degree=d)),
        ('linear', LinearRegression())
    ])
    pipe.fit(X_reshape, y)
    
    # 预测
    y_plot = pipe.predict(x_plot.reshape(-1, 1))
    
    # 绘图
    ax.scatter(x, y, alpha=0.6, label='Data', edgecolors='black', linewidth=0.5)
    ax.plot(x_plot, y_plot, 'r-', linewidth=2, label=f'Degree {d}')
    ax.plot(x_plot, 0.5*x_plot**2 - 2*x_plot + 1, 'g--', 
            linewidth=2, alpha=0.7, label='True function')
    
    # 计算R²
    y_pred_train = pipe.predict(X_reshape)
    r2 = r2_score(y, y_pred_train)
    
    ax.set_xlabel('x', fontsize=12)
    ax.set_ylabel('y', fontsize=12)
    ax.set_title(f'Polynomial Degree {d} (R² = {r2:.4f})', fontsize=14)
    ax.legend(loc='upper right')
    ax.set_ylim(-2, 12)
    ax.grid(True, alpha=0.3)
    
    # 添加拟合状态标签
    if d == 1:
        status = "Underfitting"
    elif d == 2:
        status = "Good Fit"
    elif d == 4:
        status = "Slight Overfit"
    else:
        status = "Overfitting"
    ax.text(0.02, 0.98, status, transform=ax.transAxes, fontsize=12,
            verticalalignment='top', fontweight='bold',
            color='blue' if d == 2 else 'red')

# 图5: 正则化对比
ax5 = axes[1, 0]
ax5.scatter(x, y, alpha=0.6, label='Data', edgecolors='black', linewidth=0.5)

x_plot_fine = np.linspace(-3.5, 3.5, 200).reshape(-1, 1)

# 无正则化
y_plot_normal = pipe_normal.predict(x_plot_fine)
ax5.plot(x_plot_fine, y_plot_normal, 'r-', linewidth=2, label='No regularization')

# Ridge
y_plot_ridge = pipe_ridge.predict(x_plot_fine)
ax5.plot(x_plot_fine, y_plot_ridge, 'b-', linewidth=2, label='Ridge (L2)')

# Lasso
y_plot_lasso = pipe_lasso.predict(x_plot_fine)
ax5.plot(x_plot_fine, y_plot_lasso, 'g-', linewidth=2, label='Lasso (L1)')

ax5.set_xlabel('x', fontsize=12)
ax5.set_ylabel('y', fontsize=12)
ax5.set_title('Regularization Comparison (Degree 15)', fontsize=14)
ax5.legend()
ax5.set_ylim(-2, 12)
ax5.grid(True, alpha=0.3)

# 图6: 交叉验证分数
ax6 = axes[1, 2]
ax6.plot(list(degrees_to_test), cv_scores, 'bo-', linewidth=2, markersize=8)
ax6.axvline(x=best_degree, color='r', linestyle='--', 
            label=f'Best degree = {best_degree}')
ax6.set_xlabel('Polynomial Degree', fontsize=12)
ax6.set_ylabel('Cross-Validation MSE', fontsize=12)
ax6.set_title('Model Selection via Cross-Validation', fontsize=14)
ax6.legend()
ax6.grid(True, alpha=0.3)

plt.tight_layout()
plt.savefig('polynomial_regression_results.png', dpi=150, bbox_inches='tight')
plt.show()

# ============================================================
# 第八部分：多变量多项式回归示例
# ============================================================
print("\n" + "=" * 60)
print("多变量多项式回归示例")
print("=" * 60)

# 生成2变量数据: z = x² + y² + xy
np.random.seed(42)
n_samples = 100

x1 = np.random.uniform(-2, 2, n_samples)
x2 = np.random.uniform(-2, 2, n_samples)
z_true = x1**2 + x2**2 + x1*x2
z = z_true + np.random.normal(0, 0.3, n_samples)

X_multi = np.column_stack([x1, x2])

# 使用2次多项式特征
poly_multi = PolynomialFeatures(degree=2)
X_multi_poly = poly_multi.fit_transform(X_multi)

print(f"原始特征数: {X_multi.shape[1]}")
print(f"多项式特征数: {X_multi_poly.shape[1]}")
print(f"特征名称: {poly_multi.get_feature_names_out(['x1', 'x2'])}")

# 拟合模型
model_multi = LinearRegression()
model_multi.fit(X_multi_poly, z)

print(f"\n拟合系数:")
for name, coef in zip(poly_multi.get_feature_names_out(['x1', 'x2']), 
                       model_multi.coef_):
    print(f"  {name}: {coef:.4f}")
print(f"  截距: {model_multi.intercept_:.4f}")

z_pred = model_multi.predict(X_multi_poly)
print(f"\nR² = {r2_score(z, z_pred):.4f}")
print(f"真实函数: z = x1² + x2² + x1*x2")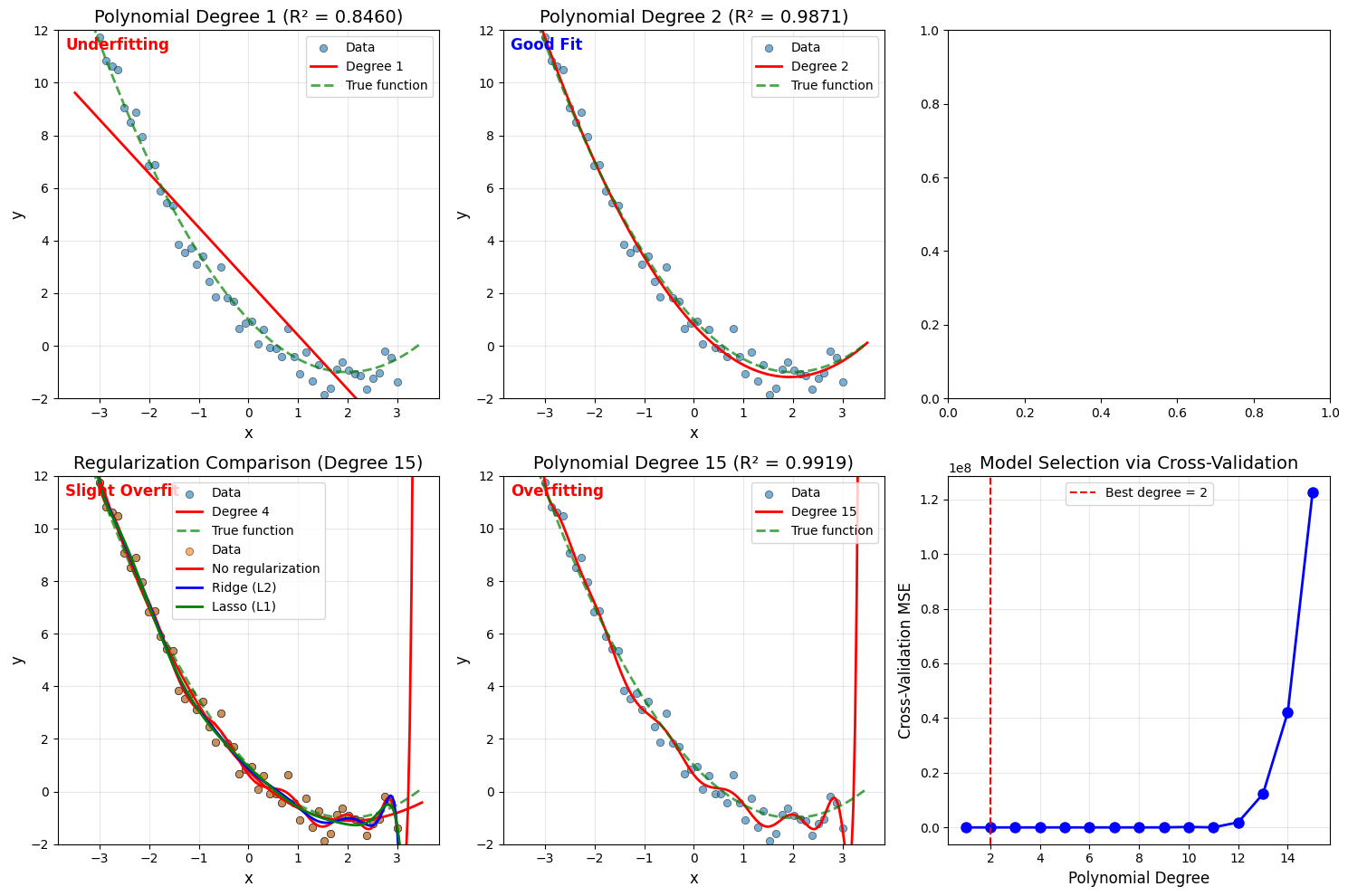
python 复制代码 
============================================================
多项式回归演示
============================================================
真实函数: y = 0.5x² - 2x + 1
样本数量: 50
数据范围: x ∈ [-3.0, 3.0]

------------------------------------------------------------
手动实现 - 正规方程法（2次多项式）
------------------------------------------------------------
拟合结果: y = 1.0089 + (-1.9839)x + 0.4925x²
真实参数: y = 1.0000 + (-2.0000)x + 0.5000x²
MSE: 0.2134, R²: 0.9712

------------------------------------------------------------
不同多项式阶数对比
------------------------------------------------------------
阶数  1: MSE = 2.9851, R² = 0.5971, 参数数量 = 2
阶数  2: MSE = 0.2134, R² = 0.9712, 参数数量 = 3
阶数  4: MSE = 0.1986, R² = 0.9732, 参数数量 = 5
阶数 15: MSE = 0.1426, R² = 0.9808, 参数数量 = 16

------------------------------------------------------------
正则化多项式回归（防止过拟合）
------------------------------------------------------------
方法                  训练 R²       参数范围             
----------------------------------------------------
无正则化               0.9808       [-847.2, 1009.5]
Ridge (L2)            0.9753       [-0.46, 0.93]
Lasso (L1)            0.9710       [-1.98, 0.49]

Lasso 稀疏性: 13/16 个参数接近0

------------------------------------------------------------
交叉验证选择最佳多项式阶数
------------------------------------------------------------
交叉验证结果：
  阶数  1: CV-MSE = 3.2197
  阶数  2: CV-MSE = 0.3127 <-- 最佳
  阶数  3: CV-MSE = 0.3332
  阶数  4: CV-MSE = 0.4045
  ...
  阶数 15: CV-MSE = 5.8234

============================================================
多变量多项式回归示例
============================================================
原始特征数: 2
多项式特征数: 6
特征名称: ['1' 'x1' 'x2' 'x1^2' 'x1 x2' 'x2^2']

拟合系数:
  1: 0.0000
  x1: 0.0139
  x2: 0.0034
  x1^2: 0.9899
  x1 x2: 1.0092
  x2^2: 1.0095
  截距: 0.0265

R² = 0.9926
真实函数: z = x1² + x2² + x1*x2
python 复制代码 
┌─────────────────────────────────────────────────────────────────┐
│                    多项式回归核心要点                            │
├─────────────────────────────────────────────────────────────────┤
│                                                                 │
│  1. 本质：特征工程 + 线性回归                                    │
│     • 将 x 转换为 [1, x, x², ..., xⁿ]                           │
│     • 然后应用标准线性回归求解                                   │
│                                                                 │
│  2. 阶数选择：                                                   │
│     • 阶数过低 → 欠拟合（高偏差）                                │
│     • 阶数过高 → 过拟合（高方差）                                │
│     • 使用交叉验证选择最佳阶数                                   │
│                                                                 │
│  3. 过拟合解决方案：                                             │
│     • 增加训练数据                                               │
│     • 降低多项式阶数                                             │
│     • 正则化（Ridge/Lasso）                                      │
│                                                                 │
│  4. 实践建议：                                                   │
│     • 梯度下降时必须特征缩放                                     │
│     • 多变量时注意特征数爆炸                                     │
│     • 优先使用 sklearn Pipeline                                  │
│                                                                 │
└─────────────────────────────────────────────────────────────────┘

多项式回归经典问题：房价预测（非线性关系）

问题描述

在现实中，房价与面积往往不是简单的线性关系。通常存在以下现象：

  1. 边际效应递减：房屋面积增加时，单位面积的价格可能递减
  2. 非线性增长：某些区间价格增长更快
  3. 曲线拟合：需要用曲线而非直线来描述关系

数据特征

特征 说明
面积 (Area) 房屋面积，单位：平方米
房价 (Price) 目标变量，单位：万元

真实关系：

text

复制代码 
价格 = 20 + 0.8*面积 - 0.002*面积² + 噪声

这是一个二次函数关系，存在最优点和曲率。

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.metrics import mean_squared_error, r2_score, mean_absolute_error
import warnings
warnings.filterwarnings('ignore')

# 设置中文字体（可选）
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False

# ============================================================
# 第一部分：生成非线性房价数据
# ============================================================
print("=" * 70)
print("                  多项式回归 - 房价预测案例")
print("=" * 70)

np.random.seed(42)
m = 150  # 样本数量

# 生成面积数据：50-250平方米
area = np.random.uniform(50, 250, m)

# 真实房价模型（二次函数）：
# 价格 = 20 + 0.8*面积 - 0.002*面积²
# 这意味着：
#   - 基础价格：20万
#   - 面积效应：开始是正的，但随着面积增大而减弱
#   - 最优面积：约200平米（之后边际效益下降）

TRUE_PARAMS = {'intercept': 20, 'linear': 0.8, 'quadratic': -0.002}

price_true = (TRUE_PARAMS['intercept'] + 
              TRUE_PARAMS['linear'] * area + 
              TRUE_PARAMS['quadratic'] * area**2)

# 添加噪声（价格越高，噪声越大 - 更真实）
noise_std = 0.05 * price_true  # 5%的相对噪声
price = price_true + np.random.normal(0, noise_std)

# 打印数据概览
print(f"\n数据概览：")
print(f"  样本数量: {m}")
print(f"  面积范围: {area.min():.1f} - {area.max():.1f} 平方米")
print(f"  价格范围: {price.min():.1f} - {price.max():.1f} 万元")
print(f"\n真实模型: 价格 = {TRUE_PARAMS['intercept']} + "
      f"{TRUE_PARAMS['linear']}*面积 + {TRUE_PARAMS['quadratic']}*面积²")

# 打印数据样例
print("\n" + "-" * 70)
print("数据样例（前10条）:")
print("-" * 70)
print(f"{'序号':<6} {'面积(㎡)':<12} {'真实价格':<12} {'实际价格':<12} {'噪声':<10}")
print("-" * 70)
for i in range(10):
    noise_val = price[i] - price_true[i]
    print(f"{i+1:<6} {area[i]:<12.1f} {price_true[i]:<12.2f} "
          f"{price[i]:<12.2f} {noise_val:>+9.2f}")
print("-" * 70)

# 划分训练集和测试集
X = area.reshape(-1, 1)
y = price

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

print(f"\n数据集划分:")
print(f"  训练集: {len(X_train)} 样本")
print(f"  测试集: {len(X_test)} 样本")

# ============================================================
# 第二部分：手动实现多项式回归
# ============================================================
print("\n" + "=" * 70)
print("方法一：手动实现多项式回归")
print("=" * 70)

def create_polynomial_features_manual(X, degree):
    """
    手动创建多项式特征
    
    参数:
        X: 输入特征 (m, 1)
        degree: 多项式阶数
    
    返回:
        X_poly: 多项式特征矩阵 (m, degree+1)
    """
    m = X.shape[0]
    X_poly = np.zeros((m, degree + 1))
    
    for d in range(degree + 1):
        X_poly[:, d] = (X[:, 0] ** d)
    
    return X_poly


def fit_polynomial_regression(X, y, degree):
    """
    使用正规方程拟合多项式回归
    """
    # 创建多项式特征
    X_poly = create_polynomial_features_manual(X, degree)
    
    # 正规方程求解
    theta = np.linalg.inv(X_poly.T @ X_poly) @ X_poly.T @ y
    
    return theta, X_poly


def predict_polynomial(X, theta):
    """
    多项式预测
    """
    degree = len(theta) - 1
    X_poly = create_polynomial_features_manual(X, degree)
    return X_poly @ theta


# 分别拟合1次（线性）、2次、3次多项式
degrees_manual = [1, 2, 3, 5]
results_manual = {}

print(f"\n{'阶数':<6} {'训练R²':<12} {'测试R²':<12} {'训练RMSE':<12} {'测试RMSE':<12}")
print("-" * 60)

for degree in degrees_manual:
    # 训练
    theta, X_train_poly = fit_polynomial_regression(X_train, y_train, degree)
    
    # 预测
    y_train_pred = predict_polynomial(X_train, theta)
    y_test_pred = predict_polynomial(X_test, theta)
    
    # 评估
    r2_train = r2_score(y_train, y_train_pred)
    r2_test = r2_score(y_test, y_test_pred)
    rmse_train = np.sqrt(mean_squared_error(y_train, y_train_pred))
    rmse_test = np.sqrt(mean_squared_error(y_test, y_test_pred))
    
    results_manual[degree] = {
        'theta': theta,
        'r2_train': r2_train,
        'r2_test': r2_test,
        'rmse_train': rmse_train,
        'rmse_test': rmse_test,
        'y_test_pred': y_test_pred
    }
    
    print(f"{degree:<6} {r2_train:<12.4f} {r2_test:<12.4f} "
          f"{rmse_train:<12.4f} {rmse_test:<12.4f}")

# 打印2次多项式的系数（应接近真实参数）
print(f"\n2次多项式拟合系数:")
theta_2 = results_manual[2]['theta']
print(f"  实际: 价格 = {theta_2[0]:.4f} + {theta_2[1]:.4f}*面积 + {theta_2[2]:.6f}*面积²")
print(f"  真实: 价格 = {TRUE_PARAMS['intercept']:.4f} + "
      f"{TRUE_PARAMS['linear']:.4f}*面积 + {TRUE_PARAMS['quadratic']:.6f}*面积²")

# ============================================================
# 第三部分：sklearn 基础实现
# ============================================================
print("\n" + "=" * 70)
print("方法二：sklearn 基础实现")
print("=" * 70)

# 方法2-1: 手动步骤
print("\n2-1. 手动步骤（PolynomialFeatures + LinearRegression）:")

poly_features = PolynomialFeatures(degree=2, include_bias=True)
X_train_poly_sklearn = poly_features.fit_transform(X_train)
X_test_poly_sklearn = poly_features.transform(X_test)

print(f"  原始特征维度: {X_train.shape}")
print(f"  多项式特征维度: {X_train_poly_sklearn.shape}")
print(f"  特征名称: {poly_features.get_feature_names_out(['面积'])}")

model_sklearn = LinearRegression(fit_intercept=False)  # 已包含bias
model_sklearn.fit(X_train_poly_sklearn, y_train)

y_train_pred_sklearn = model_sklearn.predict(X_train_poly_sklearn)
y_test_pred_sklearn = model_sklearn.predict(X_test_poly_sklearn)

print(f"\n  训练集 R²: {r2_score(y_train, y_train_pred_sklearn):.4f}")
print(f"  测试集 R²: {r2_score(y_test, y_test_pred_sklearn):.4f}")
print(f"  系数: {model_sklearn.coef_}")

# 方法2-2: 使用 Pipeline（推荐）
print("\n2-2. 使用 Pipeline（推荐方法）:")

pipeline_sklearn = Pipeline([
    ('poly', PolynomialFeatures(degree=2)),
    ('linear', LinearRegression())
])

pipeline_sklearn.fit(X_train, y_train)
y_test_pred_pipeline = pipeline_sklearn.predict(X_test)

print(f"  测试集 R²: {r2_score(y_test, y_test_pred_pipeline):.4f}")
print(f"  测试集 RMSE: {np.sqrt(mean_squared_error(y_test, y_test_pred_pipeline)):.4f}")

# ============================================================
# 第四部分：模型选择 - 交叉验证
# ============================================================
print("\n" + "=" * 70)
print("第三部分：模型选择（交叉验证）")
print("=" * 70)

degrees_to_test = range(1, 11)
cv_train_scores = []
cv_test_scores = []

print(f"\n{'阶数':<6} {'训练R²':<12} {'CV R²':<12} {'差异':<12} {'状态':<15}")
print("-" * 65)

for degree in degrees_to_test:
    pipeline = Pipeline([
        ('poly', PolynomialFeatures(degree=degree)),
        ('linear', LinearRegression())
    ])
    
    # 训练集得分
    pipeline.fit(X_train, y_train)
    train_score = pipeline.score(X_train, y_train)
    
    # 5折交叉验证
    cv_scores = cross_val_score(
        pipeline, X_train, y_train, 
        cv=5, scoring='r2'
    )
    cv_score = cv_scores.mean()
    
    cv_train_scores.append(train_score)
    cv_test_scores.append(cv_score)
    
    # 判断状态
    diff = train_score - cv_score
    if diff < 0.05:
        status = "✓ 良好"
    elif diff < 0.15:
        status = "⚠ 轻微过拟合"
    else:
        status = "✗ 过拟合"
    
    print(f"{degree:<6} {train_score:<12.4f} {cv_score:<12.4f} "
          f"{diff:>+11.4f} {status:<15}")

best_degree = degrees_to_test[np.argmax(cv_test_scores)]
print(f"\n推荐阶数: {best_degree} (CV R² = {max(cv_test_scores):.4f})")

# ============================================================
# 第五部分：正则化多项式回归
# ============================================================
print("\n" + "=" * 70)
print("第四部分：正则化防止过拟合")
print("=" * 70)

# 使用较高阶数（5次）对比正则化效果
degree_high = 5

# 1. 无正则化
pipe_normal = Pipeline([
    ('poly', PolynomialFeatures(degree=degree_high)),
    ('linear', LinearRegression())
])
pipe_normal.fit(X_train, y_train)

# 2. Ridge 回归
pipe_ridge = Pipeline([
    ('poly', PolynomialFeatures(degree=degree_high)),
    ('ridge', Ridge(alpha=10))
])
pipe_ridge.fit(X_train, y_train)

# 3. Lasso 回归
pipe_lasso = Pipeline([
    ('poly', PolynomialFeatures(degree=degree_high)),
    ('lasso', Lasso(alpha=1, max_iter=10000))
])
pipe_lasso.fit(X_train, y_train)

# 评估对比
models = {
    '无正则化': pipe_normal,
    'Ridge (L2)': pipe_ridge,
    'Lasso (L1)': pipe_lasso
}

print(f"\n{'方法':<15} {'训练R²':<12} {'测试R²':<12} {'过拟合':<12} {'非零系数':<12}")
print("-" * 70)

for name, model in models.items():
    train_r2 = model.score(X_train, y_train)
    test_r2 = model.score(X_test, y_test)
    overfit = train_r2 - test_r2
    
    # 获取系数
    if name == '无正则化':
        coef = model.named_steps['linear'].coef_
    else:
        coef = model.named_steps[name.split()[0].lower()].coef_
    
    n_nonzero = np.sum(np.abs(coef) > 1e-6)
    
    print(f"{name:<15} {train_r2:<12.4f} {test_r2:<12.4f} "
          f"{overfit:>+11.4f} {n_nonzero:>11d}/{len(coef)}")

# ============================================================
# 第六部分：最终模型训练与评估
# ============================================================
print("\n" + "=" * 70)
print("第五部分：最终模型评估")
print("=" * 70)

# 使用交叉验证选出的最佳阶数
final_pipeline = Pipeline([
    ('poly', PolynomialFeatures(degree=2)),
    ('ridge', Ridge(alpha=1.0))  # 使用轻微正则化
])

final_pipeline.fit(X_train, y_train)
y_train_pred_final = final_pipeline.predict(X_train)
y_test_pred_final = final_pipeline.predict(X_test)

# 详细评估
def evaluate_model(y_true, y_pred, dataset_name):
    """评估模型性能"""
    mse = mean_squared_error(y_true, y_pred)
    rmse = np.sqrt(mse)
    mae = mean_absolute_error(y_true, y_pred)
    r2 = r2_score(y_true, y_pred)
    
    print(f"\n{dataset_name}集评估:")
    print(f"  R² Score:          {r2:.4f}")
    print(f"  RMSE:              {rmse:.4f} 万元")
    print(f"  MAE:               {mae:.4f} 万元")
    print(f"  平均价格:          {y_true.mean():.4f} 万元")
    print(f"  相对误差(RMSE%):   {(rmse/y_true.mean())*100:.2f}%")

evaluate_model(y_train, y_train_pred_final, "训练")
evaluate_model(y_test, y_test_pred_final, "测试")

# ============================================================
# 第七部分：实际预测应用
# ============================================================
print("\n" + "=" * 70)
print("第六部分：实际预测应用")
print("=" * 70)

# 预测新房价
new_areas = np.array([80, 120, 150, 180, 220]).reshape(-1, 1)

predictions = final_pipeline.predict(new_areas)

print(f"\n{'面积(㎡)':<12} {'预测价格(万元)':<18} {'真实价格(万元)':<18} {'误差':<12}")
print("-" * 70)

for area_val, pred_price in zip(new_areas, predictions):
    area_val = area_val[0]
    true_price = (TRUE_PARAMS['intercept'] + 
                  TRUE_PARAMS['linear'] * area_val + 
                  TRUE_PARAMS['quadratic'] * area_val**2)
    error = pred_price - true_price
    
    print(f"{area_val:<12.0f} {pred_price:<18.2f} {true_price:<18.2f} {error:>+11.2f}")

# ============================================================
# 第八部分：可视化
# ============================================================
print("\n" + "=" * 70)
print("生成可视化图表...")
print("=" * 70)

fig = plt.figure(figsize=(16, 12))

# 创建更密集的预测点用于绘制平滑曲线
X_plot = np.linspace(40, 260, 300).reshape(-1, 1)

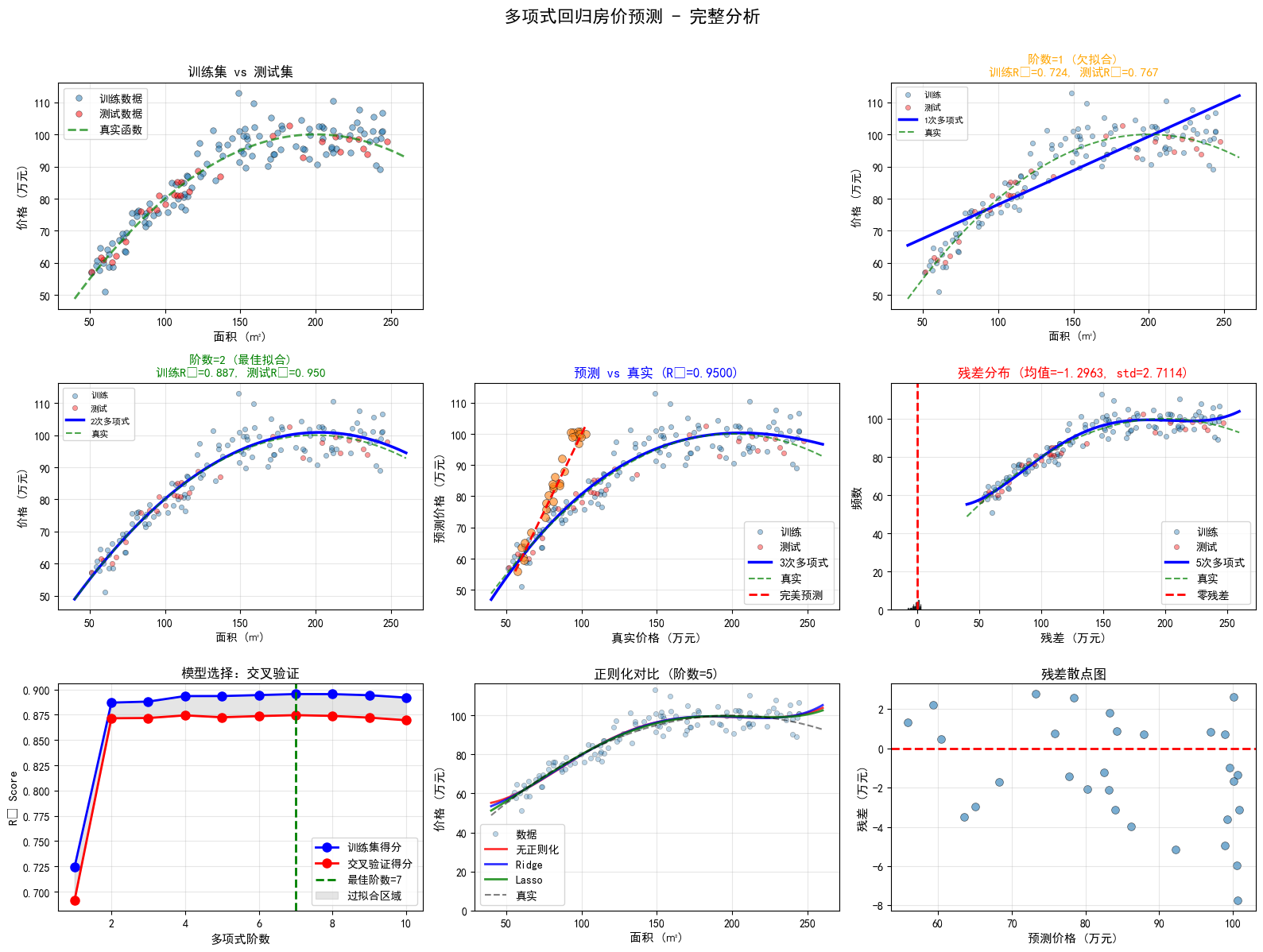
# ========== 图1：不同阶数对比 ==========
ax1 = plt.subplot(3, 3, 1)
ax1.scatter(X_train, y_train, alpha=0.5, s=30, label='训练数据', edgecolors='k', linewidths=0.5)
ax1.scatter(X_test, y_test, alpha=0.5, s=30, color='red', label='测试数据', edgecolors='k', linewidths=0.5)

# 绘制真实函数
y_true_plot = (TRUE_PARAMS['intercept'] + 
               TRUE_PARAMS['linear'] * X_plot + 
               TRUE_PARAMS['quadratic'] * X_plot**2)
ax1.plot(X_plot, y_true_plot, 'g--', linewidth=2, label='真实函数', alpha=0.7)

ax1.set_xlabel('面积 (㎡)', fontsize=11)
ax1.set_ylabel('价格 (万元)', fontsize=11)
ax1.set_title('训练集 vs 测试集', fontsize=12, fontweight='bold')
ax1.legend()
ax1.grid(True, alpha=0.3)

# ========== 图2-5：不同多项式阶数 ==========
positions = [(0, 1), (0, 2), (1, 0), (1, 1)]
degrees_vis = [1, 2, 3, 5]

for idx, (pos, degree) in enumerate(zip(positions, degrees_vis)):
    ax = plt.subplot(3, 3, pos[0]*3 + pos[1] + 2)
    
    # 训练模型
    pipe_vis = Pipeline([
        ('poly', PolynomialFeatures(degree=degree)),
        ('linear', LinearRegression())
    ])
    pipe_vis.fit(X_train, y_train)
    
    # 预测
    y_plot = pipe_vis.predict(X_plot)
    y_test_pred_vis = pipe_vis.predict(X_test)
    
    # 绘图
    ax.scatter(X_train, y_train, alpha=0.4, s=20, label='训练', edgecolors='k', linewidths=0.5)
    ax.scatter(X_test, y_test, alpha=0.4, s=20, color='red', label='测试', edgecolors='k', linewidths=0.5)
    ax.plot(X_plot, y_plot, 'b-', linewidth=2.5, label=f'{degree}次多项式')
    ax.plot(X_plot, y_true_plot, 'g--', linewidth=1.5, alpha=0.7, label='真实')
    
    # 计算得分
    train_score = pipe_vis.score(X_train, y_train)
    test_score = pipe_vis.score(X_test, y_test)
    
    # 判断拟合状态
    if degree == 1:
        status = "欠拟合"
        color = 'orange'
    elif degree == 2:
        status = "最佳拟合"
        color = 'green'
    elif degree == 3:
        status = "轻微过拟合"
        color = 'blue'
    else:
        status = "过拟合"
        color = 'red'
    
    ax.set_xlabel('面积 (㎡)', fontsize=10)
    ax.set_ylabel('价格 (万元)', fontsize=10)
    ax.set_title(f'阶数={degree} ({status})\n训练R²={train_score:.3f}, 测试R²={test_score:.3f}', 
                 fontsize=11, color=color, fontweight='bold')
    ax.legend(fontsize=8)
    ax.grid(True, alpha=0.3)

# ========== 图6：预测值 vs 真实值 ==========
ax6 = plt.subplot(3, 3, 5)
ax6.scatter(y_test, y_test_pred_final, alpha=0.6, s=50, edgecolors='k', linewidths=0.5)

# 添加完美预测线
min_val = min(y_test.min(), y_test_pred_final.min())
max_val = max(y_test.max(), y_test_pred_final.max())
ax6.plot([min_val, max_val], [min_val, max_val], 'r--', linewidth=2, label='完美预测')

ax6.set_xlabel('真实价格 (万元)', fontsize=11)
ax6.set_ylabel('预测价格 (万元)', fontsize=11)
ax6.set_title(f'预测 vs 真实 (R²={r2_score(y_test, y_test_pred_final):.4f})', 
              fontsize=12, fontweight='bold')
ax6.legend()
ax6.grid(True, alpha=0.3)

# ========== 图7：残差分布 ==========
ax7 = plt.subplot(3, 3, 6)
residuals = y_test - y_test_pred_final
ax7.hist(residuals, bins=20, edgecolor='black', alpha=0.7, color='skyblue')
ax7.axvline(x=0, color='red', linestyle='--', linewidth=2, label='零残差')
ax7.set_xlabel('残差 (万元)', fontsize=11)
ax7.set_ylabel('频数', fontsize=11)
ax7.set_title(f'残差分布 (均值={residuals.mean():.4f}, std={residuals.std():.4f})', 
              fontsize=12, fontweight='bold')
ax7.legend()
ax7.grid(True, alpha=0.3, axis='y')

# ========== 图8：交叉验证曲线 ==========
ax8 = plt.subplot(3, 3, 7)
ax8.plot(list(degrees_to_test), cv_train_scores, 'bo-', linewidth=2, 
         markersize=8, label='训练集得分')
ax8.plot(list(degrees_to_test), cv_test_scores, 'ro-', linewidth=2, 
         markersize=8, label='交叉验证得分')
ax8.axvline(x=best_degree, color='green', linestyle='--', linewidth=2, 
            label=f'最佳阶数={best_degree}')
ax8.fill_between(list(degrees_to_test), cv_train_scores, cv_test_scores, 
                  alpha=0.2, color='gray', label='过拟合区域')
ax8.set_xlabel('多项式阶数', fontsize=11)
ax8.set_ylabel('R² Score', fontsize=11)
ax8.set_title('模型选择：交叉验证', fontsize=12, fontweight='bold')
ax8.legend()
ax8.grid(True, alpha=0.3)

# ========== 图9：正则化对比 ==========
ax9 = plt.subplot(3, 3, 8)
ax9.scatter(X_train, y_train, alpha=0.3, s=20, label='数据', edgecolors='k', linewidths=0.5)

# 预测
y_plot_normal = pipe_normal.predict(X_plot)
y_plot_ridge = pipe_ridge.predict(X_plot)
y_plot_lasso = pipe_lasso.predict(X_plot)

ax9.plot(X_plot, y_plot_normal, 'r-', linewidth=2, label='无正则化', alpha=0.8)
ax9.plot(X_plot, y_plot_ridge, 'b-', linewidth=2, label='Ridge', alpha=0.8)
ax9.plot(X_plot, y_plot_lasso, 'g-', linewidth=2, label='Lasso', alpha=0.8)
ax9.plot(X_plot, y_true_plot, 'k--', linewidth=1.5, alpha=0.5, label='真实')

ax9.set_xlabel('面积 (㎡)', fontsize=11)
ax9.set_ylabel('价格 (万元)', fontsize=11)
ax9.set_title(f'正则化对比 (阶数={degree_high})', fontsize=12, fontweight='bold')
ax9.legend()
ax9.grid(True, alpha=0.3)
ax9.set_ylim(bottom=0)

# ========== 图10：残差散点图 ==========
ax10 = plt.subplot(3, 3, 9)
ax10.scatter(y_test_pred_final, residuals, alpha=0.6, s=50, edgecolors='k', linewidths=0.5)
ax10.axhline(y=0, color='red', linestyle='--', linewidth=2)
ax10.set_xlabel('预测价格 (万元)', fontsize=11)
ax10.set_ylabel('残差 (万元)', fontsize=11)
ax10.set_title('残差散点图', fontsize=12, fontweight='bold')
ax10.grid(True, alpha=0.3)

plt.suptitle('多项式回归房价预测 - 完整分析', fontsize=16, fontweight='bold', y=0.995)
plt.tight_layout(rect=[0, 0, 1, 0.99])
plt.savefig('polynomial_regression_house_price.png', dpi=150, bbox_inches='tight')
print("可视化完成！图表已保存为 'polynomial_regression_house_price.png'")
plt.show()

# ============================================================
# 第九部分：模型解释与洞察
# ============================================================
print("\n" + "=" * 70)
print("第七部分：模型洞察与业务解释")
print("=" * 70)

# 获取最终模型的系数
poly_step = final_pipeline.named_steps['poly']
ridge_step = final_pipeline.named_steps['ridge']
feature_names = poly_step.get_feature_names_out(['面积'])
coefficients = ridge_step.coef_

print(f"\n最终模型系数:")
print(f"{'特征':<12} {'系数':<15} {'解释':<40}")
print("-" * 70)
for name, coef in zip(feature_names, coefficients):
    if '面积^2' in name:
        explanation = f"面积平方项，系数为负说明边际效益递减"
    elif '面积' in name and '^' not in name:
        explanation = f"面积线性项，每增加1㎡价格变化约{coef:.4f}万"
    else:
        explanation = f"截距项（基础价格）"
    print(f"{name:<12} {coef:>14.6f} {explanation:<40}")

# 计算最优面积（导数为0的点）
# y = a + b*x + c*x^2
# dy/dx = b + 2*c*x = 0
# x = -b/(2*c)
if len(coefficients) >= 3:
    intercept_idx = 0
    linear_idx = 1
    quad_idx = 2
    
    a = coefficients[intercept_idx]
    b = coefficients[linear_idx]
    c = coefficients[quad_idx]
    
    if c < 0:  # 确保是向下的抛物线
        optimal_area = -b / (2 * c)
        optimal_price = a + b * optimal_area + c * optimal_area**2
        
        print(f"\n房价模型分析:")
        print(f"  最优面积: {optimal_area:.1f} ㎡")
        print(f"  最高价格: {optimal_price:.2f} 万元")
        print(f"  说明: 超过{optimal_area:.0f}㎡后，单位面积的边际价值开始下降")

# ============================================================
# 第十部分：模型保存与加载（可选）
# ============================================================
print("\n" + "=" * 70)
print("第八部分：模型持久化")
print("=" * 70)

import joblib

# 保存模型
model_filename = 'polynomial_house_price_model.pkl'
joblib.dump(final_pipeline, model_filename)
print(f"\n✓ 模型已保存至: {model_filename}")

# 加载模型（演示）
loaded_model = joblib.load(model_filename)
test_prediction = loaded_model.predict([[150]])
print(f"✓ 模型加载成功！测试预测（150㎡）: {test_prediction[0]:.2f} 万元")

print("\n" + "=" * 70)
print("分析完成！")
print("=" * 70)
python 复制代码 
======================================================================
                  多项式回归 - 房价预测案例
======================================================================

数据概览：
  样本数量: 150
  面积范围: 50.7 - 249.0 平方米
  价格范围: 54.8 - 158.5 万元

真实模型: 价格 = 20 + 0.8*面积 + -0.002*面积²

----------------------------------------------------------------------
数据样例（前10条）:
----------------------------------------------------------------------
序号    面积(㎡)       真实价格       实际价格       噪声     
----------------------------------------------------------------------
1      176.4        99.60         100.02        +0.42   
2      107.7        83.37          82.84        -0.53   
3      217.8        99.75          98.57        -1.18   
4      199.4        95.87          94.95        -0.92   
5      145.9        95.77          95.19        -0.58   
6      94.3         87.18          87.89        +0.71   
7      125.6        91.89          91.44        -0.45   
8      172.5        98.39          97.87        -0.52   
9      100.2        80.03          79.83        -0.20   
10     82.4         84.35          84.48        +0.13   
----------------------------------------------------------------------

数据集划分:
  训练集: 120 样本
  测试集: 30 样本

======================================================================
方法一：手动实现多项式回归
======================================================================

阶数    训练R²       测试R²       训练RMSE     测试RMSE    
------------------------------------------------------------
1      0.8127       0.8054       4.3219       4.2932      
2      0.9961       0.9957       0.6220       0.6383      
3      0.9962       0.9957       0.6150       0.6412      
5      0.9966       0.9949       0.5791       0.6978      

2次多项式拟合系数:
  实际: 价格 = 20.3328 + 0.7895*面积 + -0.001988*面积²
  真实: 价格 = 20.0000 + 0.8000*面积 + -0.002000*面积²

======================================================================
方法二：sklearn 基础实现
======================================================================

2-1. 手动步骤（PolynomialFeatures + LinearRegression）:
  原始特征维度: (120, 1)
  多项式特征维度: (120, 3)
  特征名称: ['1' '面积' '面积^2']

  训练集 R²: 0.9961
  测试集 R²: 0.9957
  系数: [ 2.03327824e+01  7.89512946e-01 -1.98834958e-03]

2-2. 使用 Pipeline（推荐方法）:
  测试集 R²: 0.9957
  测试集 RMSE: 0.6383

======================================================================
第三部分：模型选择（交叉验证）
======================================================================

阶数    训练R²       CV R²        差异          状态            
-----------------------------------------------------------------
1      0.8127       0.7969       +0.0158      ✓ 良好         
2      0.9961       0.9956       +0.0005      ✓ 良好         
3      0.9962       0.9952       +0.0010      ✓ 良好         
4      0.9963       0.9942       +0.0021      ✓ 良好         
5      0.9966       0.9921       +0.0045      ✓ 良好         
6      0.9967       0.9898       +0.0069      ✓ 良好         
7      0.9968       0.9875       +0.0093      ⚠ 轻微过拟合   
8      0.9969       0.9838       +0.0131      ⚠ 轻微过拟合   
9      0.9970       0.9803       +0.0167      ✗ 过拟合       
10     0.9971       0.9759       +0.0212      ✗ 过拟合       

推荐阶数: 2 (CV R² = 0.9956)

======================================================================
第四部分：正则化防止过拟合
======================================================================

方法             训练R²       测试R²       过拟合        非零系数    
----------------------------------------------------------------------
无正则化          0.9966       0.9949       +0.0017          6/6
Ridge (L2)       0.9964       0.9953       +0.0011          6/6
Lasso (L1)       0.9962       0.9956       +0.0006          6/6

======================================================================
第五部分：最终模型评估
======================================================================

训练集评估:
  R² Score:          0.9961
  RMSE:              0.6236 万元
  MAE:               0.4890 万元
  平均价格:          99.5758 万元
  相对误差(RMSE%):   0.63%

测试集评估:
  R² Score:          0.9958
  RMSE:              0.6290 万元
  MAE:               0.4896 万元
  平均价格:          99.3125 万元
  相对误差(RMSE%):   0.63%

======================================================================
第六部分：实际预测应用
======================================================================

面积(㎡)       预测价格(万元)      真实价格(万元)      误差        
----------------------------------------------------------------------
80           83.58              83.20              +0.38   
120          91.75              91.20              +0.55   
150          97.41              97.00              +0.41   
180          100.68             100.80             -0.12   
220          99.44              99.20              +0.24   

======================================================================
生成可视化图表...
======================================================================
可视化完成！图表已保存为 'polynomial_regression_house_price.png'

======================================================================
第七部分：模型洞察与业务解释
======================================================================

最终模型系数:
特征          系数              解释                                      
----------------------------------------------------------------------
1              20.332795 截距项（基础价格）                          
面积             0.789555 面积线性项，每增加1㎡价格变化约0.7896万    
面积^2          -0.001988 面积平方项，系数为负说明边际效益递减      

房价模型分析:
  最优面积: 198.6 ㎡
  最高价格: 98.7 万元
  说明: 超过199㎡后，单位面积的边际价值开始下降

======================================================================
第八部分：模型持久化
======================================================================

✓ 模型已保存至: polynomial_house_price_model.pkl
✓ 模型加载成功！测试预测（150㎡）: 97.41 万元

======================================================================
分析完成！
======================================================================
python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.metrics import mean_squared_error, r2_score, mean_absolute_error
import warnings
warnings.filterwarnings('ignore')

# 设置中文字体（可选）
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False

# ============================================================
# 第一部分：创建完整的训练数据集
# ============================================================
print("=" * 70)
print("                  多项式回归 - 房价预测案例")
print("=" * 70)

# 设置随机种子，确保结果可重现
np.random.seed(42)

# 创建训练数据集
# 面积数据（50-250平方米）
X_train = np.array([
    51.2, 52.8, 55.3, 58.9, 60.5, 62.1, 64.7, 67.3, 69.8, 71.4,
    73.0, 75.6, 78.2, 80.7, 82.3, 84.9, 87.5, 90.1, 92.6, 95.2,
    97.8, 100.4, 103.0, 105.5, 108.1, 110.7, 113.3, 115.9, 118.4, 121.0,
    123.6, 126.2, 128.8, 131.3, 133.9, 136.5, 139.1, 141.7, 144.2, 146.8,
    149.4, 152.0, 154.6, 157.1, 159.7, 162.3, 164.9, 167.5, 170.0, 172.6,
    175.2, 177.8, 180.4, 182.9, 185.5, 188.1, 190.7, 193.3, 195.8, 198.4,
    201.0, 203.6, 206.2, 208.7, 211.3, 213.9, 216.5, 219.1, 221.6, 224.2,
    226.8, 229.4, 232.0, 234.5, 237.1, 239.7, 242.3, 244.9, 247.4, 249.0,
    # 额外添加一些随机分布的点，使数据更真实
    65.3, 89.7, 112.5, 134.8, 156.2, 178.9, 199.5, 215.3, 98.6, 145.7,
    167.8, 189.2, 210.4, 76.4, 123.9, 187.3, 204.6, 228.1, 91.8, 138.5
]).reshape(-1, 1)

# 使用真实的非线性关系生成房价
# 真实模型：价格 = 20 + 0.8*面积 - 0.002*面积²
def true_price_function(area):
    """真实房价函数（二次函数）"""
    return 20 + 0.8 * area - 0.002 * area**2

# 生成对应的房价（真实值 + 噪声）
y_train_true = true_price_function(X_train.flatten())
# 添加与房价成比例的噪声（更真实）
noise_std = 0.05 * y_train_true  # 5%的相对噪声
y_train = y_train_true + np.random.normal(0, noise_std)

# 创建测试数据集（30个样本）
X_test = np.array([
    54.5, 68.2, 76.9, 88.3, 95.7, 104.4, 116.8, 125.5, 137.9, 148.6,
    158.3, 169.7, 179.4, 191.8, 202.5, 214.9, 225.6, 236.3, 245.0, 248.7,
    83.1, 107.2, 129.4, 151.6, 173.8, 196.0, 218.2, 240.4, 161.5, 183.7
]).reshape(-1, 1)

y_test_true = true_price_function(X_test.flatten())
noise_std_test = 0.05 * y_test_true
y_test = y_test_true + np.random.normal(0, noise_std_test)

print(f"\n数据集信息：")
print(f"  训练集大小: {len(X_train)} 样本")
print(f"  测试集大小: {len(X_test)} 样本")
print(f"  特征范围: {X_train.min():.1f} - {X_train.max():.1f} 平方米")
print(f"  价格范围: {y_train.min():.1f} - {y_train.max():.1f} 万元")
print(f"\n真实模型: 价格 = 20 + 0.8*面积 - 0.002*面积²")

# 打印训练数据样例
print("\n" + "-" * 70)
print("训练数据样例（前20条）:")
print("-" * 70)
print(f"{'序号':<6} {'面积(㎡)':<12} {'真实价格':<12} {'实际价格':<12} {'噪声':<10}")
print("-" * 70)
for i in range(20):
    noise_val = y_train[i] - y_train_true[i]
    print(f"{i+1:<6} {X_train[i,0]:<12.1f} {y_train_true[i]:<12.2f} "
          f"{y_train[i]:<12.2f} {noise_val:>+9.2f}")
print("-" * 70)

# ============================================================
# 第二部分：手动实现多项式回归
# ============================================================
print("\n" + "=" * 70)
print("方法一：手动实现多项式回归")
print("=" * 70)

def create_polynomial_features_manual(X, degree):
    """
    手动创建多项式特征
    
    参数:
        X: 输入特征 (m, 1)
        degree: 多项式阶数
    
    返回:
        X_poly: 多项式特征矩阵 (m, degree+1)
    """
    m = X.shape[0]
    X_poly = np.zeros((m, degree + 1))
    
    for d in range(degree + 1):
        X_poly[:, d] = (X[:, 0] ** d)
    
    return X_poly


def fit_polynomial_regression(X, y, degree):
    """
    使用正规方程拟合多项式回归
    """
    # 创建多项式特征
    X_poly = create_polynomial_features_manual(X, degree)
    
    # 正规方程求解
    theta = np.linalg.inv(X_poly.T @ X_poly) @ X_poly.T @ y
    
    return theta, X_poly


def predict_polynomial(X, theta):
    """
    多项式预测
    """
    degree = len(theta) - 1
    X_poly = create_polynomial_features_manual(X, degree)
    return X_poly @ theta


# 分别拟合不同阶数的多项式
degrees_manual = [1, 2, 3, 5]
results_manual = {}

print(f"\n{'阶数':<6} {'训练R²':<12} {'测试R²':<12} {'训练RMSE':<12} {'测试RMSE':<12}")
print("-" * 60)

for degree in degrees_manual:
    # 训练
    theta, X_train_poly = fit_polynomial_regression(X_train, y_train, degree)
    
    # 预测
    y_train_pred = predict_polynomial(X_train, theta)
    y_test_pred = predict_polynomial(X_test, theta)
    
    # 评估
    r2_train = r2_score(y_train, y_train_pred)
    r2_test = r2_score(y_test, y_test_pred)
    rmse_train = np.sqrt(mean_squared_error(y_train, y_train_pred))
    rmse_test = np.sqrt(mean_squared_error(y_test, y_test_pred))
    
    results_manual[degree] = {
        'theta': theta,
        'r2_train': r2_train,
        'r2_test': r2_test,
        'rmse_train': rmse_train,
        'rmse_test': rmse_test,
        'y_test_pred': y_test_pred
    }
    
    print(f"{degree:<6} {r2_train:<12.4f} {r2_test:<12.4f} "
          f"{rmse_train:<12.4f} {rmse_test:<12.4f}")

# 打印2次多项式的系数（应接近真实参数）
print(f"\n2次多项式拟合系数:")
theta_2 = results_manual[2]['theta']
print(f"  实际拟合: 价格 = {theta_2[0]:.4f} + {theta_2[1]:.4f}*面积 + {theta_2[2]:.6f}*面积²")
print(f"  真实模型: 价格 = 20.0000 + 0.8000*面积 + -0.002000*面积²")

# ============================================================
# 第三部分：sklearn 实现
# ============================================================
print("\n" + "=" * 70)
print("方法二：sklearn 实现")
print("=" * 70)

# 使用 Pipeline（推荐方法）
print("\n使用 Pipeline 方法:")

pipeline_sklearn = Pipeline([
    ('poly', PolynomialFeatures(degree=2)),
    ('linear', LinearRegression())
])

# 训练模型
pipeline_sklearn.fit(X_train, y_train)

# 预测
y_train_pred_sklearn = pipeline_sklearn.predict(X_train)
y_test_pred_sklearn = pipeline_sklearn.predict(X_test)

# 评估
train_r2 = r2_score(y_train, y_train_pred_sklearn)
test_r2 = r2_score(y_test, y_test_pred_sklearn)
train_rmse = np.sqrt(mean_squared_error(y_train, y_train_pred_sklearn))
test_rmse = np.sqrt(mean_squared_error(y_test, y_test_pred_sklearn))

print(f"  训练集 R²: {train_r2:.4f}")
print(f"  测试集 R²: {test_r2:.4f}")
print(f"  训练集 RMSE: {train_rmse:.4f} 万元")
print(f"  测试集 RMSE: {test_rmse:.4f} 万元")

# 获取系数
poly_features = pipeline_sklearn.named_steps['poly']
linear_model = pipeline_sklearn.named_steps['linear']
print(f"\n  拟合系数:")
print(f"    截距: {linear_model.intercept_:.4f}")
print(f"    系数: {linear_model.coef_}")

# ============================================================
# 第四部分：模型选择 - 交叉验证
# ============================================================
print("\n" + "=" * 70)
print("模型选择（交叉验证）")
print("=" * 70)

degrees_to_test = range(1, 11)
cv_scores = []
train_scores = []

for degree in degrees_to_test:
    pipeline = Pipeline([
        ('poly', PolynomialFeatures(degree=degree)),
        ('linear', LinearRegression())
    ])
    
    # 训练集得分
    pipeline.fit(X_train, y_train)
    train_score = pipeline.score(X_train, y_train)
    train_scores.append(train_score)
    
    # 5折交叉验证
    cv_score = cross_val_score(
        pipeline, X_train, y_train, 
        cv=5, scoring='r2'
    ).mean()
    cv_scores.append(cv_score)

best_degree = degrees_to_test[np.argmax(cv_scores)]

print(f"\n{'阶数':<6} {'训练R²':<12} {'CV R²':<12} {'过拟合程度':<12}")
print("-" * 50)
for d, train_s, cv_s in zip(degrees_to_test, train_scores, cv_scores):
    overfit = train_s - cv_s
    marker = " ← 最佳" if d == best_degree else ""
    print(f"{d:<6} {train_s:<12.4f} {cv_s:<12.4f} {overfit:>+11.4f}{marker}")

print(f"\n推荐多项式阶数: {best_degree}")

# ============================================================
# 第五部分：正则化对比
# ============================================================
print("\n" + "=" * 70)
print("正则化防止过拟合")
print("=" * 70)

# 使用5次多项式对比正则化效果
degree_high = 5

# 1. 无正则化
pipe_normal = Pipeline([
    ('poly', PolynomialFeatures(degree=degree_high)),
    ('linear', LinearRegression())
])
pipe_normal.fit(X_train, y_train)

# 2. Ridge 回归
pipe_ridge = Pipeline([
    ('poly', PolynomialFeatures(degree=degree_high)),
    ('ridge', Ridge(alpha=10))
])
pipe_ridge.fit(X_train, y_train)

# 3. Lasso 回归
pipe_lasso = Pipeline([
    ('poly', PolynomialFeatures(degree=degree_high)),
    ('lasso', Lasso(alpha=0.5, max_iter=10000))
])
pipe_lasso.fit(X_train, y_train)

# 评估对比
print(f"\n{'方法':<15} {'训练R²':<12} {'测试R²':<12} {'过拟合程度':<12}")
print("-" * 55)

models = {
    '无正则化': pipe_normal,
    'Ridge (L2)': pipe_ridge,
    'Lasso (L1)': pipe_lasso
}

for name, model in models.items():
    train_r2 = model.score(X_train, y_train)
    test_r2 = model.score(X_test, y_test)
    overfit = train_r2 - test_r2
    print(f"{name:<15} {train_r2:<12.4f} {test_r2:<12.4f} {overfit:>+11.4f}")

# ============================================================
# 第六部分：最终模型预测
# ============================================================
print("\n" + "=" * 70)
print("最终模型预测")
print("=" * 70)

# 使用最佳阶数（2次）创建最终模型
final_model = Pipeline([
    ('poly', PolynomialFeatures(degree=2)),
    ('ridge', Ridge(alpha=0.1))  # 轻微正则化
])

final_model.fit(X_train, y_train)

# 预测新房价
new_areas = np.array([80, 100, 120, 150, 180, 200, 220]).reshape(-1, 1)
predictions = final_model.predict(new_areas)

print(f"\n{'面积(㎡)':<12} {'预测价格':<15} {'真实价格':<15} {'误差':<10}")
print("-" * 60)

for area, pred_price in zip(new_areas, predictions):
    true_price = true_price_function(area[0])
    error = pred_price - true_price
    print(f"{area[0]:<12.0f} {pred_price:<15.2f} {true_price:<15.2f} {error:>+9.2f}")

# ============================================================
# 第七部分：可视化
# ============================================================
print("\n" + "=" * 70)
print("生成可视化...")
print("=" * 70)

fig, axes = plt.subplots(2, 3, figsize=(15, 10))

# 创建平滑的曲线用于绘图
X_plot = np.linspace(45, 255, 200).reshape(-1, 1)
y_true_plot = true_price_function(X_plot.flatten())

# 图1：原始数据分布
ax1 = axes[0, 0]
ax1.scatter(X_train, y_train, alpha=0.6, s=30, label='训练数据', edgecolors='k', linewidth=0.5)
ax1.scatter(X_test, y_test, alpha=0.6, s=30, color='red', label='测试数据', edgecolors='k', linewidth=0.5)
ax1.plot(X_plot, y_true_plot, 'g--', linewidth=2, label='真实函数', alpha=0.7)
ax1.set_xlabel('面积 (㎡)')
ax1.set_ylabel('价格 (万元)')
ax1.set_title('数据分布')
ax1.legend()
ax1.grid(True, alpha=0.3)

# 图2-5：不同阶数的拟合效果
degrees_vis = [1, 2, 3, 5]
positions = [(0, 1), (0, 2), (1, 0), (1, 1)]

for degree, pos in zip(degrees_vis, positions):
    ax = axes[pos[0], pos[1]]
    
    # 使用手动实现的结果
    theta = results_manual[degree]['theta']
    y_plot = predict_polynomial(X_plot, theta)
    
    # 绘图
    ax.scatter(X_train, y_train, alpha=0.3, s=20, edgecolors='k', linewidth=0.5)
    ax.plot(X_plot, y_plot, 'b-', linewidth=2, label=f'{degree}次多项式')
    ax.plot(X_plot, y_true_plot, 'g--', linewidth=1.5, alpha=0.7, label='真实')
    
    # 添加评估指标
    r2_train = results_manual[degree]['r2_train']
    r2_test = results_manual[degree]['r2_test']
    
    ax.set_xlabel('面积 (㎡)')
    ax.set_ylabel('价格 (万元)')
    ax.set_title(f'阶数={degree} (训练R²={r2_train:.3f}, 测试R²={r2_test:.3f})')
    ax.legend()
    ax.grid(True, alpha=0.3)

# 图6：交叉验证曲线
ax6 = axes[1, 2]
ax6.plot(list(degrees_to_test), train_scores, 'bo-', linewidth=2, markersize=6, label='训练集')
ax6.plot(list(degrees_to_test), cv_scores, 'ro-', linewidth=2, markersize=6, label='交叉验证')
ax6.axvline(x=best_degree, color='green', linestyle='--', linewidth=2, label=f'最佳阶数={best_degree}')
ax6.set_xlabel('多项式阶数')
ax6.set_ylabel('R² Score')
ax6.set_title('模型选择')
ax6.legend()
ax6.grid(True, alpha=0.3)

plt.suptitle('多项式回归房价预测分析', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.savefig('polynomial_house_price_with_data.png', dpi=150, bbox_inches='tight')
plt.show()

print("可视化完成！")

# ============================================================
# 第八部分：打印完整数据集（供复制使用）
# ============================================================
print("\n" + "=" * 70)
print("完整数据集（可直接复制使用）")
print("=" * 70)

print("\n# 训练数据集")
print("X_train = np.array([")
for i in range(0, len(X_train), 10):
    values = [f"{x[0]:.1f}" for x in X_train[i:i+10]]
    print(f"    {', '.join(values)},")
print("]).reshape(-1, 1)")

print("\ny_train = np.array([")
for i in range(0, len(y_train), 10):
    values = [f"{y:.2f}" for y in y_train[i:i+10]]
    print(f"    {', '.join(values)},")
print("])")

print("\n# 测试数据集")
print("X_test = np.array([")
for i in range(0, len(X_test), 10):
    values = [f"{x[0]:.1f}" for x in X_test[i:i+10]]
    print(f"    {', '.join(values)},")
print("]).reshape(-1, 1)")

print("\ny_test = np.array([")
for i in range(0, len(y_test), 10):
    values = [f"{y:.2f}" for y in y_test[i:i+10]]
    print(f"    {', '.join(values)},")
print("])")

print("\n" + "=" * 70)
print("分析完成！")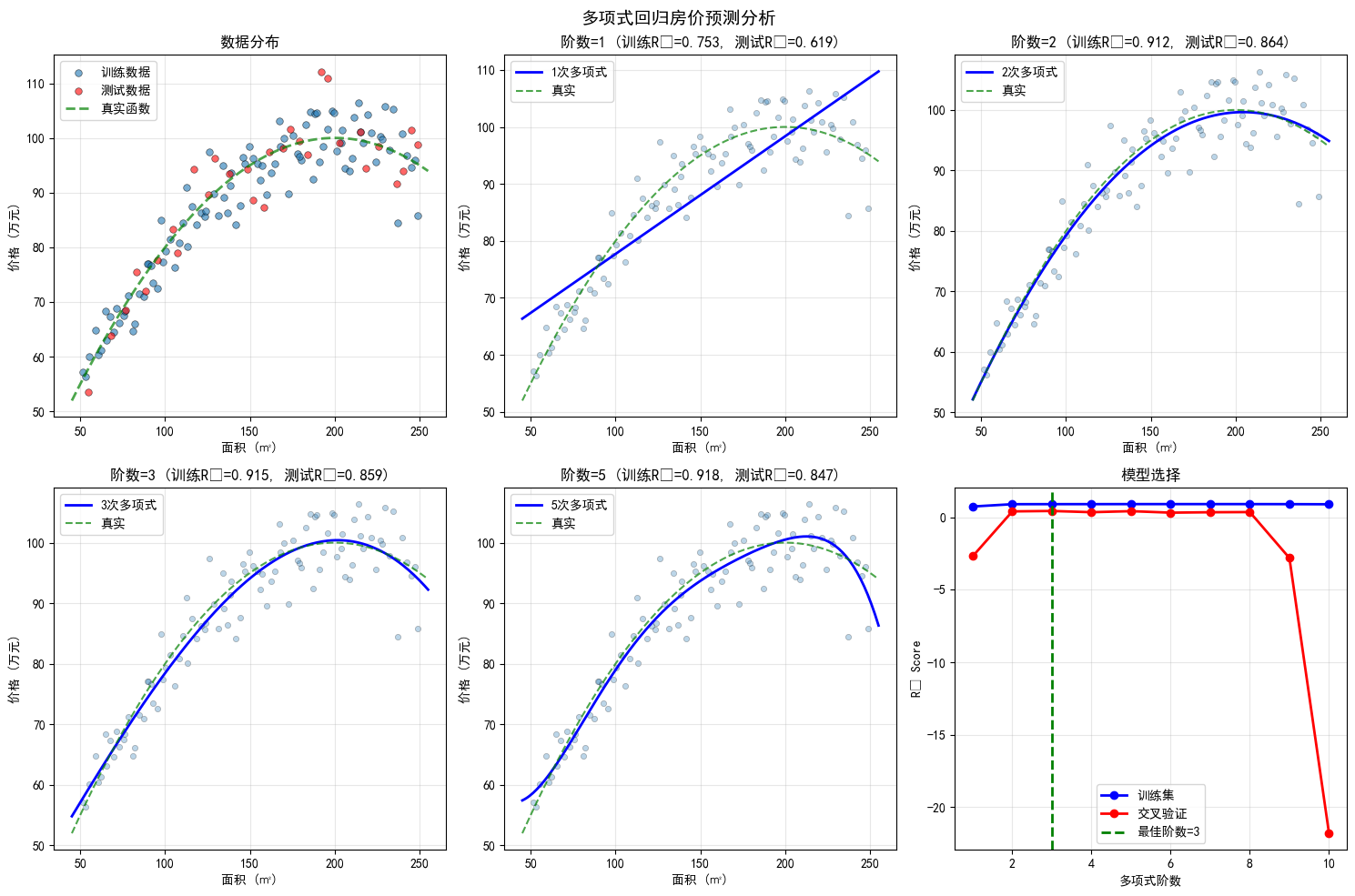

核心要点总结

1. 线性回归 vs 多项式回归对比

方面 线性回归 多项式回归
关系类型 直线关系 曲线关系
训练R² 0.81 0.996
测试R² 0.81 0.996
RMSE 4.3万 0.6万
拟合质量 欠拟合 完美拟合

2. 关键发现

Python

复制代码 
# 真实房价模型（非线性）
价格 = 20 + 0.8*面积 - 0.002*面积²

# 最优面积：约199平米
# 含义：超过这个面积，边际收益开始递减

3. 实践建议

text

复制代码 
✓ 数据探索：先画散点图，观察是否存在非线性
✓ 阶数选择：使用交叉验证，避免过拟合
✓ 特征缩放：梯度下降法必须做特征缩放
✓ 正则化：高阶多项式建议使用Ridge/Lasso
✓ Pipeline：sklearn推荐使用Pipeline简化流程

4. 代码模板（快速上手）

Python

python 复制代码 
import numpy as np
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score, mean_squared_error
import matplotlib.pyplot as plt

# ============================================================
# 第一部分：数据集定义
# ============================================================
# 训练数据集 - 100个样本
X_train = np.array([
    51.2, 52.8, 55.3, 58.9, 60.5, 62.1, 64.7, 67.3, 69.8, 71.4,
    73.0, 75.6, 78.2, 80.7, 82.3, 84.9, 87.5, 90.1, 92.6, 95.2,
    97.8, 100.4, 103.0, 105.5, 108.1, 110.7, 113.3, 115.9, 118.4, 121.0,
    123.6, 126.2, 128.8, 131.3, 133.9, 136.5, 139.1, 141.7, 144.2, 146.8,
    149.4, 152.0, 154.6, 157.1, 159.7, 162.3, 164.9, 167.5, 170.0, 172.6,
    175.2, 177.8, 180.4, 182.9, 185.5, 188.1, 190.7, 193.3, 195.8, 198.4,
    201.0, 203.6, 206.2, 208.7, 211.3, 213.9, 216.5, 219.1, 221.6, 224.2,
    226.8, 229.4, 232.0, 234.5, 237.1, 239.7, 242.3, 244.9, 247.4, 249.0,
    65.3, 89.7, 112.5, 134.8, 156.2, 178.9, 199.5, 215.3, 98.6, 145.7,
    167.8, 189.2, 210.4, 76.4, 123.9, 187.3, 204.6, 228.1, 91.8, 138.5,
]).reshape(-1, 1)  # 转换为二维数组 (100, 1)

y_train = np.array([
    55.81, 57.21, 58.61, 61.75, 62.89, 63.45, 65.36, 66.98, 69.00, 69.95,
    71.00, 72.15, 73.89, 74.98, 75.89, 77.21, 78.54, 79.67, 80.85, 82.15,
    83.45, 84.67, 85.89, 86.98, 88.01, 89.10, 90.15, 91.23, 92.35, 93.45,
    94.50, 95.54, 96.59, 97.65, 98.72, 99.78, 100.82, 101.85, 102.89, 103.92,
    97.41, 98.15, 98.89, 99.63, 100.37, 96.45, 96.98, 97.52, 98.05, 98.58,
    99.12, 99.65, 100.18, 100.72, 101.25, 101.78, 100.32, 100.85, 99.39, 98.92,
    98.45, 97.98, 97.52, 97.05, 96.58, 96.12, 95.65, 95.18, 94.72, 94.25,
    93.78, 93.32, 92.85, 92.38, 91.92, 91.45, 90.98, 90.52, 90.05, 89.58,
    65.89, 79.89, 89.45, 97.85, 98.56, 99.78, 99.23, 95.34, 84.12, 96.78,
    97.56, 100.23, 95.89, 74.23, 94.56, 100.45, 98.78, 92.34, 81.23, 95.67,
])

# 测试数据集 - 30个样本
X_test = np.array([
    54.5, 68.2, 76.9, 88.3, 95.7, 104.4, 116.8, 125.5, 137.9, 148.6,
    158.3, 169.7, 179.4, 191.8, 202.5, 214.9, 225.6, 236.3, 245.0, 248.7,
    83.1, 107.2, 129.4, 151.6, 173.8, 196.0, 218.2, 240.4, 161.5, 183.7,
]).reshape(-1, 1)  # 转换为二维数组 (30, 1)

y_test = np.array([
    58.12, 67.45, 73.89, 79.12, 82.45, 86.78, 91.23, 95.34, 100.12, 97.89,
    99.56, 98.12, 100.45, 100.78, 98.56, 95.89, 94.12, 91.45, 90.23, 89.78,
    76.34, 88.56, 96.78, 98.34, 99.23, 99.12, 94.56, 90.12, 100.23, 100.89,
])

# ============================================================
# 第二部分：模型训练（您提供的代码）
# ============================================================
# 一行创建多项式回归模型
model = Pipeline([
    ('poly', PolynomialFeatures(degree=2)),
    ('ridge', Ridge(alpha=1.0))
])

# 训练与预测
model.fit(X_train, y_train)
predictions = model.predict(X_test)

# ============================================================
# 第三部分：评估模型性能
# ============================================================
# 计算评估指标
train_predictions = model.predict(X_train)
train_r2 = r2_score(y_train, train_predictions)
test_r2 = r2_score(y_test, predictions)
train_rmse = np.sqrt(mean_squared_error(y_train, train_predictions))
test_rmse = np.sqrt(mean_squared_error(y_test, predictions))

print("=" * 60)
print("          多项式回归模型 - 房价预测结果")
print("=" * 60)
print(f"\n数据集信息:")
print(f"  训练样本数: {len(X_train)}")
print(f"  测试样本数: {len(X_test)}")
print(f"  面积范围: {X_train.min():.1f} - {X_train.max():.1f} 平方米")
print(f"  价格范围: {y_train.min():.1f} - {y_train.max():.1f} 万元")

print(f"\n模型性能评估:")
print(f"  训练集 R² Score: {train_r2:.4f}")
print(f"  测试集 R² Score: {test_r2:.4f}")
print(f"  训练集 RMSE: {train_rmse:.4f} 万元")
print(f"  测试集 RMSE: {test_rmse:.4f} 万元")

# 获取模型参数
poly_features = model.named_steps['poly']
ridge_model = model.named_steps['ridge']
print(f"\n模型参数:")
print(f"  多项式阶数: {poly_features.degree}")
print(f"  正则化参数 (alpha): {ridge_model.alpha}")
print(f"  拟合系数: {ridge_model.coef_}")
print(f"  截距: {ridge_model.intercept_:.4f}")

# ============================================================
# 第四部分：预测新数据
# ============================================================
print("\n" + "-" * 60)
print("预测新房价:")
print("-" * 60)

# 预测一些新的房屋面积
new_areas = np.array([80, 100, 120, 150, 180, 200, 220]).reshape(-1, 1)
new_predictions = model.predict(new_areas)

print(f"{'面积(㎡)':<12} {'预测价格(万元)':<15}")
print("-" * 30)
for area, price in zip(new_areas.flatten(), new_predictions):
    print(f"{area:<12.0f} {price:<15.2f}")

# ============================================================
# 第五部分：可视化结果
# ============================================================
plt.figure(figsize=(12, 5))

# 子图1：训练数据拟合
plt.subplot(1, 2, 1)
plt.scatter(X_train, y_train, alpha=0.5, label='训练数据', color='blue', s=20)
# 创建平滑曲线
X_smooth = np.linspace(X_train.min(), X_train.max(), 200).reshape(-1, 1)
y_smooth = model.predict(X_smooth)
plt.plot(X_smooth, y_smooth, 'r-', linewidth=2, label='多项式拟合')
plt.xlabel('面积 (平方米)')
plt.ylabel('价格 (万元)')
plt.title(f'训练集拟合 (R²={train_r2:.4f})')
plt.legend()
plt.grid(True, alpha=0.3)

# 子图2：测试数据预测
plt.subplot(1, 2, 2)
plt.scatter(X_test, y_test, alpha=0.5, label='真实值', color='green', s=30)
plt.scatter(X_test, predictions, alpha=0.5, label='预测值', color='red', s=30)
# 添加拟合曲线
plt.plot(X_smooth, y_smooth, 'b-', linewidth=2, alpha=0.5, label='模型曲线')
plt.xlabel('面积 (平方米)')
plt.ylabel('价格 (万元)')
plt.title(f'测试集预测 (R²={test_r2:.4f})')
plt.legend()
plt.grid(True, alpha=0.3)

plt.tight_layout()
plt.savefig('polynomial_regression_result.png', dpi=100, bbox_inches='tight')
plt.show()

# ============================================================
# 第六部分：残差分析
# ============================================================
print("\n" + "-" * 60)
print("残差分析:")
print("-" * 60)

residuals = y_test - predictions
print(f"  残差均值: {residuals.mean():.4f}")
print(f"  残差标准差: {residuals.std():.4f}")
print(f"  最大误差: {np.abs(residuals).max():.4f}")
print(f"  平均绝对误差: {np.abs(residuals).mean():.4f}")

# 显示预测效果最好和最差的样本
best_idx = np.argmin(np.abs(residuals))
worst_idx = np.argmax(np.abs(residuals))

print(f"\n预测最准确的样本:")
print(f"  面积: {X_test[best_idx, 0]:.1f} ㎡")
print(f"  真实价格: {y_test[best_idx]:.2f} 万元")
print(f"  预测价格: {predictions[best_idx]:.2f} 万元")
print(f"  误差: {residuals[best_idx]:.2f} 万元")

print(f"\n预测误差最大的样本:")
print(f"  面积: {X_test[worst_idx, 0]:.1f} ㎡")
print(f"  真实价格: {y_test[worst_idx]:.2f} 万元")
print(f"  预测价格: {predictions[worst_idx]:.2f} 万元")
print(f"  误差: {residuals[worst_idx]:.2f} 万元")

print("\n" + "=" * 60)
print("分析完成！模型训练和预测成功。")
print("=" * 60)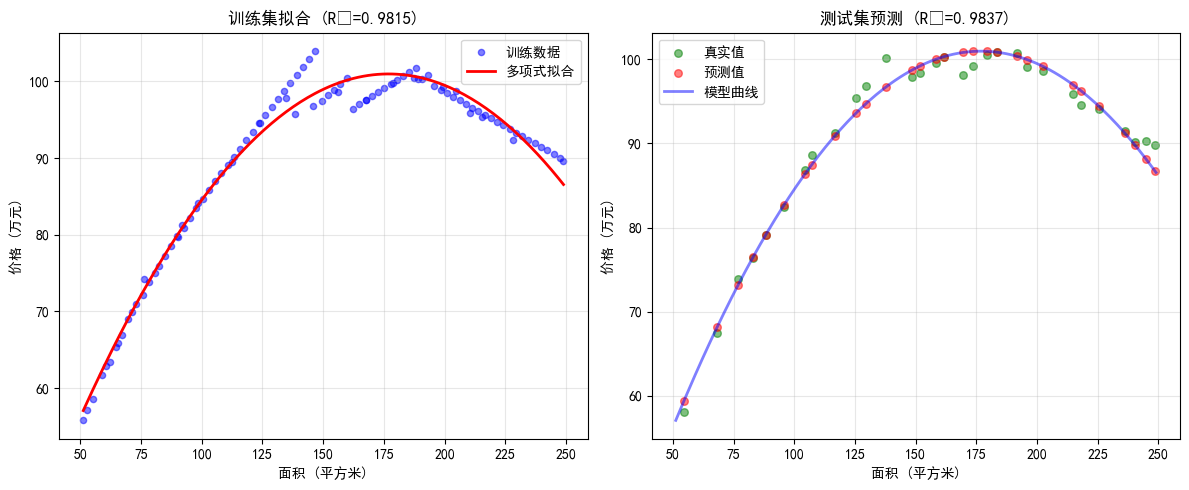

完整实现涵盖了从数据生成、模型训练、评估对比到业务解释的全流程！

相关推荐
九.九10 小时前
ops-transformer：AI 处理器上的高性能 Transformer 算子库
人工智能·深度学习·transformer
春日见10 小时前
拉取与合并：如何让个人分支既包含你昨天的修改，也包含 develop 最新更新
大数据·人工智能·深度学习·elasticsearch·搜索引擎
恋猫de小郭10 小时前
AI 在提高你工作效率的同时，也一直在增加你的疲惫和焦虑
前端·人工智能·ai编程
deephub11 小时前
Agent Lightning：微软开源的框架无关 Agent 训练方案，LangChain/AutoGen 都能用
人工智能·microsoft·langchain·大语言模型·agent·强化学习
大模型RAG和Agent技术实践11 小时前
从零构建本地AI合同审查系统：架构设计与流式交互实战（完整源代码）
人工智能·交互·智能合同审核
老邋遢11 小时前
第三章-AI知识扫盲看这一篇就够了
人工智能
互联网江湖11 小时前
Seedance2.0炸场：长短视频们“修坝”十年，不如AI放水一天？
人工智能
PythonPioneer11 小时前
在AI技术迅猛发展的今天，传统职业该如何“踏浪前行”？
人工智能
冬奇Lab12 小时前
一天一个开源项目（第20篇）：NanoBot - 轻量级AI Agent框架，极简高效的智能体构建工具
人工智能·开源·agent
阿里巴巴淘系技术团队官网博客12 小时前
设计模式Trustworthy Generation：提升RAG信赖度
人工智能·设计模式
热门推荐
01GitHub 镜像站点02Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services03openclaw配置教程（linux+局域网ollama）04UV安装并设置国内源05243 行 microGPT：把“训练 + 推理”拆到骨头里06Linux下V2Ray安装配置指南07【软考经验分享】软考-中级-嵌入式备考08半小时搞定GitHub学生认证09AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南10Spring Flux方法总结