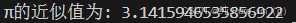寒假Python班作业（一）

第一题

题目：

计算下列多项式之和：

1+12\frac{1}{2}21+13\frac{1}{3}31+14\frac{1}{4}41+...+1100\frac{1}{100}1001

代码：

python 复制代码

num=0
for i in range(1,101):
    num+=1/i
print("该多项式和为：",num)

运行结果：

第二题

题目：

1-12\frac{1}{2}21+13\frac{1}{3}31-14\frac{1}{4}41+15\frac{1}{5}51...+1n\frac{1}{n}n1

代码：

python 复制代码

num=0
n=int(input("请输入n值："))
for i in range(1,n+1):
    if i%2==1:
        num+=1/i
    else:
        num-=1/i
print("该多项式和为：",num)

运行结果：

第三题

题目：

1+11+2\frac{1}{1+2}1+21+11+2+3\frac{1}{1+2+3}1+2+31+...+11+2+...+n\frac{1}{1+2+...+n}1+2+...+n1

代码：

python 复制代码

num=0
deno=0
n=int(input("请输入n值："))
for i in range(1,n+1):
    deno+=i
    num+=1/deno
print("该多项式和为：",num)

运行结果：

第四题

题目：

计算a+aa+aaa+a...a前6项之和（a=2）

代码：

python 复制代码

num=0
a=2
pre=6
corrent=0
for i in range(pre):
    corrent+=10**i*a
    num+=corrent
print("a+aa+aaa+aa...a前6项之和（a=2）为：",num)

运行结果：

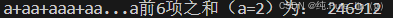
第五题

题目：

用泰勒级数计算e的近似值，直到最后一项小于1e-6为止，

e=1+11!\frac{1}{1!}1!1+12!\frac{1}{2!}2!1+13!\frac{1}{3!}3!1+...+1n!\frac{1}{n!}n!1

代码：

python 复制代码

e=1
deno=1
n=1
term=1
while term>=1e-6:
    for i in range(1,n+1):
        deno*=i
    term=1/deno
    e+=term
    n+=1
    deno=1
print(e)

运行结果：

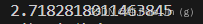
第六题

题目：

计算n的公式为：π4\frac{ \pi}{4}4π=1-13\frac{1}{3}31+15\frac{1}{5}51-17\frac{1}{7}71+...

计算的近似值。

代码：

python 复制代码

quarter_pi=0
deno=1  
term=1
sign=1
while abs(term)>=1e-6:
    term=sign/deno
    quarter_pi+=term
    sign*=-1  
    deno+=2  
print("π的近似值为:" ,quarter_pi*4)

运行结果：