MATLAB 电流/电压FFT谐波分析程序代码分析文档

本文档为FFT谐波分析程序最终稳定版的专属代码分析文档，与实际可运行代码完全对应。文档从代码结构、模块功能、核心算法、关键语句、数据流转 五个核心维度，全面解析代码实现逻辑------既明确各模块的工程业务作用，也详细阐释核心代码的底层原理，兼顾功能快速理解 与算法细节深挖，可直接作为工程应用参考、代码二次开发指导及相关技术培训资料。

一、代码整体概述

1.1 核心定位

本程序基于MATLAB原生语法开发，是一款离线式电流/电压谐波分析工具 ，专门针对CSV格式的等时间间隔采样数据，实现从数据读取、信号预处理到结果可视化的全流程自动化谐波分析。程序核心依托MATLAB自带的fft函数完成快速傅里叶变换，结合科学的信号预处理策略抑制频谱泄漏，最终精准输出各次谐波的幅值、相位、频率及总谐波畸变率（THD），满足工程场景下的谐波分析需求。

1.2 整体结构

代码遵循功能解耦的工程设计原则，划分为9个核心功能模块及1个可选结果导出模块。各模块间通过变量实现单向数据流转，无循环依赖问题，执行流程线性清晰。所有可配置参数均集中在代码开头区域，后续功能模块无需修改，大幅提升了代码的可维护性与易用性，符合工程代码的标准化设计要求。

1.3 核心特性

语法兼容性强：基于MATLAB R2024b开发，兼容R2019a及以上所有版本，无需依赖任何第三方库，调用MATLAB原生函数即可正常运行；
鲁棒性优异：各关键执行步骤均添加了数据有效性判断及报错/警告机制，可有效避免空数据、采样数据不足等异常情况导致的程序崩溃；
算法严谨可靠：集成直流分量去除、整数基波周期截取等预处理步骤，可有效抑制频谱泄漏现象，确保FFT谐波分析的精度符合工程标准；
可扩展性良好：采用模块解耦设计，可单独修改某一功能模块（如数据读取、谐波提取、结果可视化等），快速实现功能升级与扩展。

1.4 关键变量流转图

核心参数配置 → 分析类型定义 → CSV数据读取（sig）→ 信号预处理（sig_fft）→ FFT计算（Y/A/phase_deg）→ 谐波提取（harmonic结构体）→ 结果输出+THD计算 → 可视化

二、模块逐行/逐块代码分析

模块1：核心参数可配置区（第1节）

功能定位

该区域是程序唯一需要人工修改的部分，主要用于集中管理所有与实际采样数据、谐波分析需求相关的配置参数。所有参数修改后全局生效，无需调整后续任何功能模块的代码，极大降低了人工操作成本与出错概率。

核心代码

Matlab 复制代码

excel_path = 'data.csv';   % CSV数据文件路径
sheet_name = 1;             % CSV兼容参数，固定为1
data_col = 6;               % 目标数据列号
start_row = 18;              % 数据读取起始行
Fs = 2500000;                  % 采样频率 [Hz]
f0 = 50;                    % 基波频率 [Hz]
harmonic_order = 20;        % 最高分析谐波次数
is_voltage = false;         % 分析类型切换（电压/电流）

代码解析

路径参数excel_path：支持相对路径（要求CSV文件与程序脚本置于同一文件夹）和绝对路径（如'D:\sampling\data.csv'），文件后缀需固定为.csv，确保适配程序数据读取模块的xlsread函数；
兼容参数sheet_name：由于CSV文件不具备Excel的"工作表"功能，该参数仅为适配xlsread函数的入参要求，固定设置为1即可，无实际工程业务意义；
采样频率Fs：本程序设置为2.5MHz，属于典型的过采样（分析20次50Hz谐波仅需采样频率大于2000Hz）。过采样可有效提高FFT频率分辨率，减少离散频率轴与理论谐波频率的匹配误差；
开关参数is_voltage：布尔型变量，用于切换分析类型（电压/电流），是后续结果标注、单位显示的核心判断依据，仅影响结果展示形式，不改变核心计算逻辑。

设计亮点

采用参数集中管理模式，严格遵循"一处修改，全局生效"的工程设计原则，大幅降低人工操作失误率，提升代码的易用性与可维护性。

模块2：分析类型与标注定义（第2节）

功能定位

根据核心参数区的is_voltage开关参数，自动定义信号名称、物理单位等标注信息，为后续控制台结果输出、可视化图表标注提供统一的全局变量，避免在多个模块中重复编写if-else判断语句，简化代码结构，提升代码可维护性。

核心代码

Matlab 复制代码

if is_voltage
    sig_name = '电压';      % 信号名称变量
    unit = 'V';             % 物理单位变量
else
    sig_name = '电流';
    unit = 'A';
end

代码解析

定义两个全局标注变量 ：sig_name（字符型，用于存储信号名称，即"电压"或"电流"）和unit（字符型，用于存储物理单位，即"V"或"A"），后续所有需要标注信号类型、物理单位的场景，直接调用该两个变量即可；
变量命名遵循语义化原则，sig_name对应"signal name"（信号名称），unit对应"物理单位"，见名知意，便于后续代码阅读与二次开发。

设计亮点

将标注逻辑与核心计算逻辑完全解耦，后续若需新增分析类型（如功率分析），仅需在此模块中增加对应分支判断，无需修改其他任何功能模块，扩展性极强。

模块3：CSV数据读取与预处理（第3节）

功能定位

该模块的核心功能是从CSV文件的指定行、指定列读取采样数据，完成数据清洗 （剔除空值/NaN无效数据）与数据有效性判断 ，最终输出纯净的一维数值采样序列sig，为后续信号预处理、FFT计算提供可靠的基础数据。

核心代码

Matlab 复制代码

[~, ~, raw] = xlsread(excel_path, sheet_name);
data = cell2mat(raw(start_row:end, data_col)); % 从起始行截取指定列
sig = data(~isnan(data)); % 剔除空值/NaN
sig = sig(~isnan(sig));
N = length(sig);            % 有效采样点数
if N == 0
    error('读取的数据为空！请检查Excel路径、起始行、数据列是否正确');
end

代码解析

xlsread函数调用：
1. 入参：CSV文件路径excel_path、兼容参数sheet_name；
2. 出参：[~, ~, raw]，其中~用于忽略无实际意义的输出（数值矩阵、文本矩阵），仅保留单元格原始数据raw（cell类型），可完美适配CSV文件"表头+数值"的混合格式；
3. 关键特性：MATLAB的xlsread函数原生支持CSV文件读取，无需额外进行格式转换，兼容性强，操作便捷。
raw(start_row:end, data_col)：实现采样数据的精准行/列定位与截取，start_row:end表示从指定起始行读取至文件最后一行，data_col表示目标采样数据所在的列号，确保读取的数据准确无误；
cell2mat函数：将cell类型的截取数据转换为MATLAB可直接进行计算的**data** 数值矩阵，是连接cell类型与数值类型数据的核心转换工具；
数据清洗sig = data(~isnan(data))：
1. isnan(data)：判断data矩阵中是否存在NaN（空值/无效值），返回与data同维度的布尔矩阵，其中NaN对应位置为"true"，有效数值对应位置为"false"；
2. ~isnan(data)：对布尔矩阵进行取反操作，得到有效数值的索引位置；
3. 重复执行该清洗操作，可双重保障采样数据的纯净度，避免CSV文件中大量连续空值导致的无效数据残留。
有效采样点数计算N = length(sig)：由于sig为一维数值数组，length函数可直接返回其元素个数，即有效采样点数，为后续信号预处理提供关键参数；
有效性判断if N == 0：若有效采样点数为0，通过error函数抛出终止性报错，并明确给出排查方向（检查文件路径、起始行、数据列），避免后续模块对空数据进行无效计算，导致程序崩溃。

关键注意点

程序运行前，务必确保CSV采样文件处于关闭状态 ，否则xlsread函数无法正常读取文件数据，会导致有效采样点数N=0，进而触发报错，影响程序正常执行。

模块4：信号预处理（第4节）

功能定位

对模块3输出的纯净采样序列sig，进行直流分量去除 与整数基波周期截取 两项核心预处理操作，最终输出预处理后的信号sig_fft。该模块的核心目的是抑制频谱泄漏，确保后续FFT谐波分析的精度，是整个谐波分析流程中最关键的预处理环节。

核心代码

Matlab 复制代码

sig = sig - mean(sig);      % 去除直流分量
T0 = 1/f0;                  % 基波周期 [s]
N0 = round(Fs * T0);        % 单个基波周期的采样点数
n_cycle = floor(N / N0);    % 整数个基波周期数
if n_cycle < 1
    error('有效采样数据不足1个基波周期！请增加采样点或检查采样/基波频率');
end
N_fft = n_cycle * N0;       % FFT的有效采样点数（整数周期）
sig_fft = sig(1:N_fft);     % 截取后用于FFT的信号

代码解析

去除直流分量sig = sig - mean(sig)：
1. 原理：实际工程中的采样信号通常会包含直流偏移（信号均值非0），而直流分量对应FFT变换后的0频信号，会干扰低频谐波的精准提取，因此需在FFT计算前彻底去除；
2. mean(sig)：计算采样序列sig的均值，该均值即为信号中包含的直流分量大小；
3. 操作：用原始采样信号减去其直流分量，得到零均值的交流采样序列，为后续FFT谐波分析提供纯净的信号源。
基波周期计算T0 = 1/f0：根据核心参数区设置的基波频率f0，计算基波的周期（单位：秒），例如50Hz基波的周期为0.02s，符合工频电力系统的标准要求；
单周期采样点数N0 = round(Fs * T0)：
1. 原理：根据采样定理，采样频率与基波周期的乘积即为单个基波周期内的采样点数，即Fs = N0 / T0；
2. round函数：由于Fs和f0均为整数，两者乘积可能为小数，而采样点数必须为整数，因此需通过round函数进行四舍五入取整；
3. 示例：当Fs=2.5MHz、f0=50Hz时，N0=round(2500000×0.02)=50000，即单个50Hz基波周期内包含50000个采样点。
整数周期数计算n_cycle = floor(N / N0)：
1. floor函数：对有效采样点数N与单周期采样点数N0的比值进行向下取整，得到采样序列中包含的最大整数个基波周期数；
2. 原理：FFT算法对"非整数周期信号"进行变换时，会出现频谱泄漏现象（谐波能量向相邻频率扩散），导致谐波幅值、相位的计算误差，因此必须截取整数个基波周期的信号进行FFT计算。
周期数有效性判断if n_cycle < 1：若有效采样点数不足1个基波周期，通过error函数抛出终止性报错，并给出明确排查方向（增加采样点、检查采样频率/基波频率），避免后续FFT计算无意义；
FFT有效点数N_fft = n_cycle * N0：整数基波周期数与单周期采样点数的乘积，即为用于FFT计算的有效采样点数，该数值为整数且是基波周期的整数倍，可彻底消除频谱泄漏根源；
信号截取sig_fft = sig(1:N_fft)：从原始纯净采样序列的开头，截取N_fft个采样点，得到整数个基波周期的零均值采样序列，为后续FFT核心计算提供合格的输入信号。

算法核心

整数基波周期截取 是抑制频谱泄漏的最有效方法之一，与窗函数法（如汉宁窗、汉明窗）相比，该方法无幅值衰减问题，可更精准地提取各次谐波的幅值与相位，更适用于工程场景下的精准谐波分析。

模块5：FFT核心计算（第5节）

功能定位

对模块4输出的预处理信号sig_fft，执行快速傅里叶变换（FFT） ，计算得到单边频谱幅值 （经归一化处理，与实际物理值一致）、相位角 （转换为角度制，便于工程读取）和频率轴，为后续各次谐波分量提取提供核心数据支撑。

核心代码

Matlab 复制代码

Y = fft(sig_fft);           % 快速傅里叶变换
f = (0:N_fft-1)*(Fs/N_fft); % FFT对应的频率轴 [Hz]
A = 2 * abs(Y(1:N_fft/2+1)) / N_fft; % 单边频谱幅值
phase_rad = angle(Y(1:N_fft/2+1));
phase_rad(A < 1e-6) = 0;    % 去除小幅值相位噪声
phase_deg = rad2deg(phase_rad); % 相位转换为角度 [°]
f_half = f(1:N_fft/2+1);    % 单边频率轴（0~Fs/2）

代码解析

快速傅里叶变换Y = fft(sig_fft)：
1. 入参：预处理后的整数周期信号sig_fft（一维数值数组）；
2. 出参：Y（复数数组），其长度与sig_fft一致（即N_fft），复数的模对应各频率点的幅值，复数的辐角对应各频率点的相位（弧度制）；
3. 算法特性：MATLAB的fft函数为优化后的快速傅里叶变换算法，计算效率远高于传统傅里叶变换，可高效处理2.5MHz采样频率下的海量采样数据。
完整频率轴计算f = (0:N_fft-1)*(Fs/N_fft)：
1. 原理：FFT变换的频率分辨率df = Fs / N_fft，即相邻两个频率点的间隔，频率分辨率越小，谐波频率匹配精度越高；
2. 频率轴范围：0 ~ Fs - df，共包含N_fft个频率点，呈线性均匀分布；
3. 示例：当Fs=2.5MHz、N_fft=50000时，频率分辨率df=2500000/50000=50Hz，频率轴为0、50、100、...、2499950Hz，覆盖完整的采样频率范围。
单边频谱幅值计算A = 2 * abs(Y(1:N_fft/2+1)) / N_fft：
1. 关键背景：实信号的FFT变换结果具有共轭对称性，即前半段（0~Fs/2）与后半段（Fs/2~Fs）的幅值完全一致、相位相反，因此仅需分析前半段单边频谱，即可获取所有有效谐波信息，同时大幅减少计算量；
2. 分步解析：
  - Y(1:N_fft/2+1)：截取FFT变换结果的前半段，包含0频信号和Fs/2频信号，与单边频谱的频率范围对应；
  - abs(Y)：计算复数数组Y的模，得到各频率点的未归一化幅值；
  - 2 * ... / N_fft：幅值归一化操作，将FFT计算得到的相对幅值转换为实际物理幅值：
    - 乘以2：补偿单边频谱的幅值损失（共轭对称性导致后半段幅值叠加到前半段，需乘以2还原实际幅值）；
    - 除以N_fft：消除FFT采样点数的缩放效应，确保归一化后的幅值与原始采样数据的物理单位一致（V/A）。
3. 核心作用：归一化后的A即为各频率点的实际物理幅值，可直接用于后续谐波分析，无需额外进行单位换算或幅值校正。
相位计算（弧度制）phase_rad = angle(Y(1:N_fft/2+1))：
1. angle(Y)：计算复数数组Y的辐角，得到各频率点的相位（单位：弧度），相位范围为[-π, π]；
2. 截取FFT结果的前半段，确保相位数据与单边频谱幅值A、频率轴f_half一一对应。
相位噪声去除phase_rad(A < 1e-6) = 0：
1. 原理：幅值远小于1e-6的频率点属于噪声点，其相位无实际工程意义，且会出现随机波动，干扰谐波相位的精准读取，因此需将该类噪声点的相位置0；
2. 操作：通过幅值索引A < 1e-6，定位所有噪声点，将其对应的相位值置0，确保相位结果的有效性与准确性。
相位转换为角度制phase_deg = rad2deg(phase_rad)：通过rad2deg函数，将弧度制相位转换为角度制相位 ，相位范围转换为[-180°, 180°]，更符合工程人员的阅读习惯与工程标准要求；
单边频率轴f_half = f(1:N_fft/2+1)：截取完整频率轴的前半段，与单边频谱幅值A、角度制相位phase_deg一一对应，频率范围为0 ~ Fs/2，完全符合奈奎斯特采样准则（采样频率需大于2倍最高信号频率）。

核心关键点

幅值归一化操作 是本模块的核心，直接决定谐波幅值的计算精度。若缺少2/N_fft的归一化操作，FFT计算得到的幅值将与实际物理值偏差极大，无法用于工程场景下的谐波分析与评估。

模块6：各次谐波分量提取（第6节）

功能定位

基于模块5输出的单边频率轴f_half、归一化幅值A、角度制相位phase_deg，精准提取1~harmonic_order次谐波的实际频率、实际幅值、实际相位 ，并通过MATLAB自定义结构体harmonic集中存储所有谐波参数，便于后续结果输出、可视化及二次调用。

核心代码

Matlab 复制代码

harmonic = struct('order', [], 'freq', [], 'amplitude', [], 'phase_deg', []);
for k = 1:harmonic_order
    f_k = k * f0;           % 第k次谐波的理论频率
    [~, idx] = min(abs(f_half - f_k)); % 匹配离散频率轴中最接近的点
    harmonic.order(k) = k;
    harmonic.freq(k) = f_half(idx);    % 实际匹配的频率
    harmonic.amplitude(k) = A(idx);    % 谐波幅值
    harmonic.phase_deg(k) = phase_deg(idx); % 谐波相位（°）
end

代码解析

结构体初始化harmonic = struct(...)：
1. 采用MATLAB原生struct函数，创建用于存储谐波参数的自定义结构体，包含4个语义化字段，字段功能清晰：
  - order：谐波次数，取值范围为1,2,...,harmonic_order；
  - freq：各次谐波的实际匹配频率（Hz），与离散频率轴对应；
  - amplitude：各次谐波的实际幅值（V/A），为归一化后的实际物理值；
  - phase_deg：各次谐波的实际相位（°），为去除噪声后的角度制相位。
2. 优势：采用结构体存储谐波参数，可将相关联的谐波信息集中管理，相比多个独立数组，更便于数据的读取、调用、修改及导出（如导出至Excel）。
循环提取谐波for k = 1:harmonic_order：通过for循环，遍历1到最高谐波次数（harmonic_order），逐次提取各次谐波的核心参数，实现谐波提取的自动化；
理论谐波频率f_k = k * f0：根据工程定义，第k次谐波的理论频率为基波频率的k倍，例如50Hz基波的3次谐波理论频率为150Hz，5次谐波理论频率为250Hz；
离散频率轴匹配[~, idx] = min(abs(f_half - f_k))：
1. 核心问题：FFT变换后的频率轴f_half是离散分布 的（间隔为频率分辨率df），而谐波理论频率f_k是连续的，可能未恰好落在离散频率点上，因此需通过匹配算法找到最接近的离散频率点；
2. 分步解析：
  - f_half - f_k：计算单边频率轴上所有离散频率点与第k次谐波理论频率的差值；
  - abs(...)：对差值取绝对值，得到各离散频率点与理论频率的绝对偏差；
  - min(...)：找到绝对偏差的最小值 ，其对应的索引idx，即为离散频率轴上最接近理论谐波频率的点；
  - ~：忽略绝对偏差的最小值本身，仅保留对应的索引idx，用于后续参数提取。
3. 示例：当频率分辨率df=50Hz时，50Hz基波的理论频率恰好落在离散频率点上，索引idx对应该频率点，匹配无偏差。
谐波参数赋值：通过索引idx，从单边频率轴f_half、归一化幅值A、角度制相位phase_deg中，提取对应离散频率点的参数，赋值给结构体harmonic的相应字段，实现各次谐波参数的精准提取与存储。

算法核心

离散频率轴的最小误差匹配 ，解决了FFT频率轴离散性与谐波理论频率连续性的矛盾，确保谐波参数提取的准确性。匹配误差由频率分辨率df决定，df越小，匹配误差越小，谐波参数提取精度越高。

模块7：控制台结果输出（第7节）

功能定位

将程序的核心配置参数 和各次谐波提取结果 ，以标准化表格形式输出到MATLAB控制台。输出内容语义清晰、格式规范，符合工程报告的阅读习惯，便于工程人员快速查看、核对谐波分析结果。

核心代码

Matlab 复制代码

fprintf('===================== %s 谐波分析结果 =====================\n', sig_name);
fprintf('采样频率：%d Hz | 基波频率：%d Hz | 最高分析谐波：%d次\n', Fs, f0, harmonic_order);
fprintf('读取起始行：%d | 有效采样点数：%d | 分析周期数：%d个基波周期\n\n', start_row, N_fft, n_cycle);
fprintf('次谐波\t理论频率(Hz)\t实际频率(Hz)\t幅值\t\t相位(°)\n');
fprintf('--------------------------------------------------------\n');
for k = 1:harmonic_order
    fprintf('%d\t\t%.2f\t\t%.2f\t\t%.4f\t\t%.2f\n', ...
        harmonic.order(k), k*f0, harmonic.freq(k), ...
        harmonic.amplitude(k), harmonic.phase_deg(k));
end

代码解析

fprintf函数：MATLAB原生的格式化输出函数 ，核心功能是将变量按指定格式输出到控制台，支持字符串拼接、数值格式化、制表符\t（实现表格对齐）、换行符\n（实现换行），可灵活实现多样化输出格式；
标题输出：通过%s占位符，调用全局标注变量sig_name，自动切换输出标题为"电压谐波分析结果"或"电流谐波分析结果"，适配不同分析类型；
核心配置参数输出：通过%d（整数格式）占位符，依次输出采样频率、基波频率、最高分析谐波次数、读取起始行、有效采样点数、分析周期数等核心参数，用|分隔各参数，排版清晰，便于快速核对；
表格表头输出：通过制表符\t分隔各列标题，构建标准化表格表头，表头包含"次谐波、理论频率(Hz)、实际频率(Hz)、幅值、相位(°)"，与后续谐波数据一一对应，结构清晰；
分隔线输出：通过连续的-绘制表格分隔线，清晰区分表头与数据区域，提升表格可读性；
谐波数据循环输出：
1. 通过for循环，遍历各次谐波，按表格格式输出每一次谐波的参数，采用不同格式化占位符，适配不同类型数值：
  - %d：整数格式，输出谐波次数（无小数）；
  - %.2f：保留2位小数，输出理论频率、实际频率、相位，符合工程数据的精度要求；
  - %.4f：保留4位小数，输出谐波幅值，进一步提升幅值数据的精度，满足精准谐波分析需求。
2. 通过制表符\t分隔各列数据，确保表格对齐，输出结果可直接复制到工程报告中使用，无需额外整理。

设计亮点

采用格式化、表格化输出方式，结合语义化标题，无需人工整理输出结果，控制台输出内容可直接复制到工程报告、技术文档中，大幅提升工程人员的工作效率。

模块8：总谐波畸变率（THD）计算（第8节）

功能定位

按照国标谐波分析公式 ，计算信号的总谐波畸变率（THD，单位：%）。THD是评价信号谐波含量的核心工程指标，直接反映信号偏离理想正弦波的程度。计算完成后，将THD结果输出到控制台，同时在基波幅值过小时给出警告提示，确保计算结果的有效性。

核心代码

Matlab 复制代码

A1 = harmonic.amplitude(1); % 基波幅值
if A1 < 1e-6
    warning('基波幅值接近0，THD计算无意义！');
else
    A_harm = harmonic.amplitude(2:end); % 2次及以上谐波幅值
    THD = sqrt(sum(A_harm.^2)) / A1 * 100; % THD计算公式（%）
    fprintf('\n%s总谐波畸变率 THD = %.2f %% \n', sig_name, THD);
end

代码解析

基波幅值提取A1 = harmonic.amplitude(1)：1次谐波即为基波，从结构体harmonic的amplitude字段中，提取第1个元素，作为基波幅值，用于THD计算（THD公式中分母为基波幅值）；
基波幅值有效性判断if A1 < 1e-6：
1. 若基波幅值接近0（小于1e-6），说明采样信号中无明显基波成分（可能为噪声信号，或基波频率设置错误），此时计算THD无实际工程意义；
2. 通过warning函数抛出非终止性警告 ，提示工程人员排查问题，程序不会终止运行，区别于error函数的终止性报错。
谐波幅值提取A_harm = harmonic.amplitude(2:end)：提取2次及以上所有谐波的幅值，组成一维数值数组A_harm，对应THD公式中分子部分的谐波幅值；
THD计算公式THD = sqrt(sum(A_harm.^2)) / A1 * 100：
1. 国标公式：$$THD = \frac{\sqrt{U_2^2 + U_3^2 + ... + U_n^2}}{U_1} \times 100\%$$（电压信号），电流信号的THD计算公式完全一致，仅变量符号不同；
2. 分步解析：
  - A_harm.^2：对2次及以上谐波的幅值，进行逐元素平方，得到各次谐波幅值的平方值；
  - sum(...)：计算所有谐波幅值平方值的和，即U_2^2 + U_3^2 + ... + U_n^2；
  - sqrt(...)：对谐波幅值平方和进行开平方运算，得到谐波幅值的方均根，即\sqrt{U_2^2 + U_3^2 + ... + U_n^2}；
  - 除以A1（基波幅值），得到标幺值形式的THD；
  - 乘以100，将标幺值转换为百分比形式（%），符合工程场景下THD的常用表示方法。
THD结果输出：通过fprintf函数，将THD结果输出到控制台，保留2位小数，同时通过sig_name变量，自动切换输出为"电压总谐波畸变率"或"电流总谐波畸变率"，适配不同分析类型。

工程意义

THD值的大小，直接反映信号的谐波污染程度：THD越小，说明信号越接近理想正弦波，谐波含量越低，对电力系统、电子设备的干扰越小；在工频电力系统中，通常要求THD<5%，若THD超过该阈值，会导致电网畸变、设备损耗增加、电气设备异常运行等问题。

模块9：结果可视化（第9节）

功能定位

自动生成原始波形图（时域） 和**FFT单边频谱图（频域）**的组合可视化窗口，直观展示采样信号的时域特性（波形畸变情况）和频域特性（谐波分布情况）。各次谐波点用红色圆点精准标注，便于工程人员快速定位谐波位置，分析信号畸变的根源。

核心代码

Matlab 复制代码

figure('Color','w','Position',[100,100,1200,600]); % 新建图形窗口
% 子图1：整数周期原始波形图
subplot(1,2,1);
t = (0:N_fft-1)/Fs; % 时间轴 [s]
plot(t, sig_fft, 'b-', 'LineWidth',1.2);
xlabel('时间 t (s)');
ylabel([sig_name, ' (', unit, ')']);
title([num2str(n_cycle), '个基波周期的', sig_name, '波形']);
grid on; grid minor;
% 子图2：FFT单边频谱图
subplot(1,2,2);
plot(f_half, A, 'b-', 'LineWidth',1.2);
hold on;
plot(harmonic.freq, harmonic.amplitude, 'ro', 'MarkerSize',6, 'DisplayName','各次谐波');
xlabel('频率 f (Hz)');
ylabel(['幅值 (', unit, ')']);
title([sig_name, ' FFT频谱（基波', num2str(f0), 'Hz）']);
xlim([0, (harmonic_order+1)*f0]);
grid on; grid minor;
legend('Location','best');
hold off;

代码解析

9.1 图形窗口初始化

figure('Color','w','Position',[100,100,1200,600])：新建一个独立的图形可视化窗口，用于展示时域波形图和频域频谱图；Color','w：设置图形窗口背景为白色，避免灰色背景影响图表清晰度，同时适合报告截图、打印使用；Position',[100,100,1200,600]：设置图形窗口的位置（左上角坐标为(100,100)）和大小（宽度1200像素、高度600像素），尺寸适中，便于工程人员观察图表细节。

9.2 子图1：整数基波周期原始波形图（时域）

subplot(1,2,1)：将新建的图形窗口，划分为1行2列的子图布局，激活第1个子图（左侧子图），用于绘制时域原始波形图；
时间轴计算t = (0:N_fft-1)/Fs：
1. 生成与预处理信号sig_fft同长度的时间轴（单位：秒），时间轴上的每个点，对应一个采样点的时间坐标；
2. 原理：采样点的时间坐标=采样点索引×采样间隔，其中采样间隔Ts = 1/Fs。
绘制波形plot(t, sig_fft, 'b-', 'LineWidth',1.2)：
1. 入参说明：t（横坐标，时间轴）、sig_fft（纵坐标，预处理后的采样信号）、b-（蓝色实线，用于绘制波形）、LineWidth',1.2（线宽1.2像素，确保波形清晰可见）；
2. 核心作用：绘制预处理后的整数周期原始波形，直观展示信号的时域畸变情况，便于工程人员快速判断信号是否偏离理想正弦波。
坐标轴标注xlabel/ylabel：
1. 横坐标标注为"时间 t (s)"，明确时间轴的物理意义和单位；
2. 纵坐标通过字符串拼接[sig_name, ' (', unit, ')']，自动标注为"电压 (V)"或"电流 (A)"，适配不同分析类型，标注规范、清晰。
标题title：通过num2str函数，将整数基波周期数n_cycle转换为字符串，拼接成语义化标题（如"5个基波周期的电流波形"），明确图表展示的内容；
网格显示grid on; grid minor：

结果展示

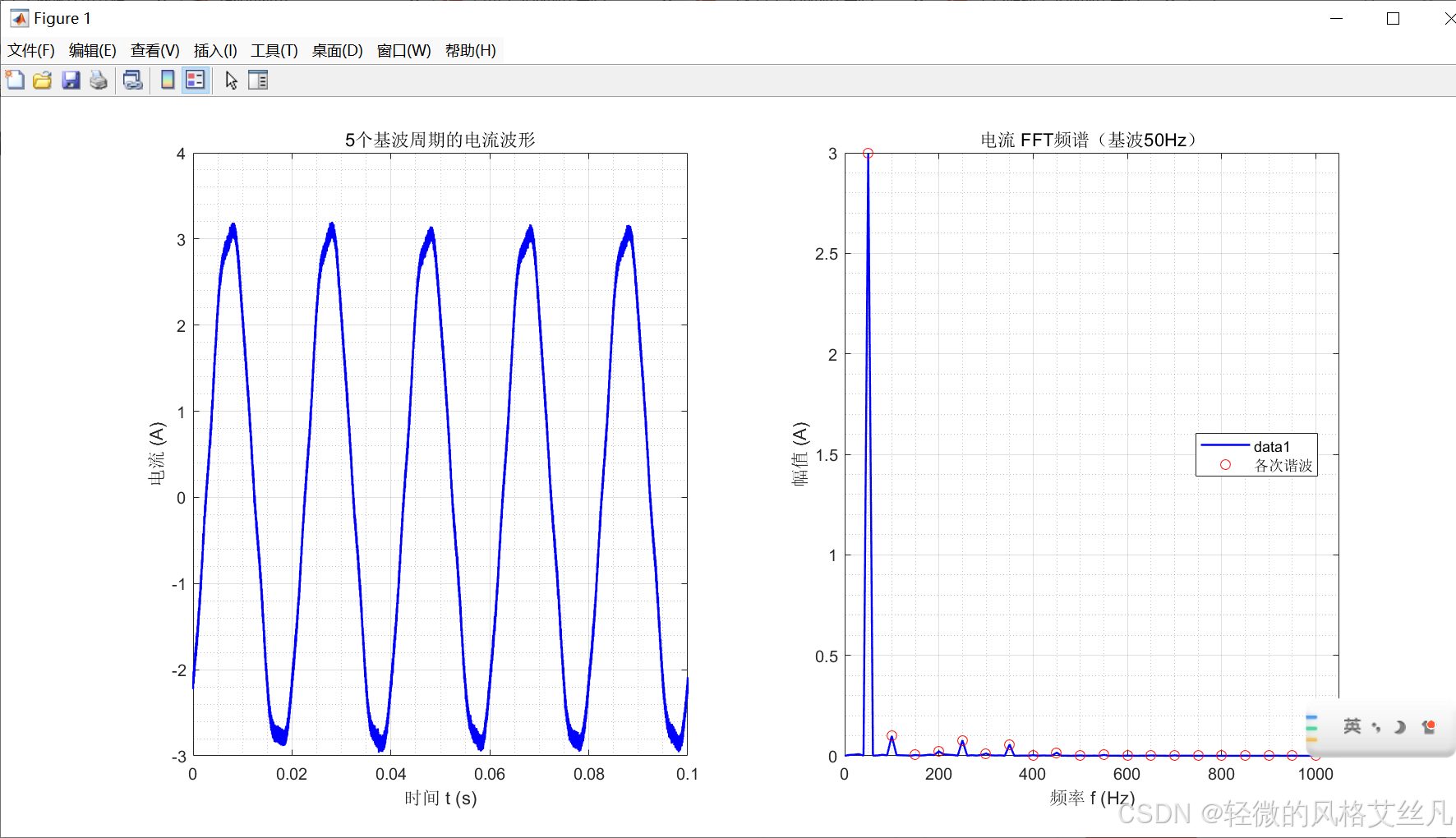
代码源码

Matlab 复制代码

%% ===================== 1. 核心参数可配置区（重点：修改这里！）=====================
excel_path = 'data.csv';   % Excel文件路径（含文件名，如'E:\test\current.xlsx'）
sheet_name = 1;             % 读取的工作表：数字（第1张）或字符串（如'Sheet1'）
data_col = 6;               % 电压/电流数据所在列（第1列写1，第2列写2）
start_row = 18;              % 读取起始行【关键】：从第N行开始读，跳过前N-1行（如表头在第1行，就设2）
Fs = 2500000;                  % 采样频率 [Hz]，需满足奈奎斯特准则（>2*最高次谐波频率）
f0 = 50;                    % 基波频率 [Hz]，如工频50Hz、变频60Hz
harmonic_order = 20;        % 需计算的最高次谐波（如10/20/30次，按需修改）
is_voltage = false;%true;          % true=分析电压，false=分析电流（仅影响结果标注）

%% ===================== 2. 定义标注字符串（替换三目运算符，MATLAB原生写法）=====================
% 根据is_voltage判断，定义电压/电流标注字符串，后续统一调用
if is_voltage
    sig_name = '电压';      % 信号名称（用于输出和标题）
    unit = 'V';             % 物理单位（V/伏，A/安）
else
    sig_name = '电流';
    unit = 'A';
end

%% ===================== 3. 读取Excel数据（指定起始行）=====================
[~, ~, raw] = xlsread(excel_path, sheet_name);
data = cell2mat(raw(start_row:end, data_col)); % 从起始行截取指定列
sig = data(~isnan(data)); % 剔除空值/NaN
% 统一剔除空值和非数值，保证数据纯净
sig = sig(~isnan(sig));
N = length(sig);            % 有效采样点数
if N == 0
    error('读取的数据为空！请检查Excel路径、起始行、数据列是否正确');
end

%% ===================== 4. 信号预处理（去直流+截取整数基波周期，抑制频谱泄漏）=====================
sig = sig - mean(sig);      % 去除直流分量（谐波分析必备，排除0频干扰）
T0 = 1/f0;                  % 基波周期 [s]
N0 = round(Fs * T0);        % 每个基波周期的采样点数
n_cycle = floor(N / N0);    % 整数个基波周期数
if n_cycle < 1
    error('有效采样数据不足1个基波周期！请增加采样点或检查采样/基波频率');
end
N_fft = n_cycle * N0;       % FFT的有效采样点数（整数周期）
sig_fft = sig(1:N_fft);     % 截取后用于FFT的信号

%% ===================== 5. FFT核心计算（幅值+相位归一化）=====================
Y = fft(sig_fft);           % 快速傅里叶变换
f = (0:N_fft-1)*(Fs/N_fft); % FFT对应的频率轴 [Hz]
% 计算单边频谱幅值（归一化，保证幅值为实际物理值）
A = 2 * abs(Y(1:N_fft/2+1)) / N_fft;
% 计算相位（弧度转角度，去除小幅值相位噪声）
phase_rad = angle(Y(1:N_fft/2+1));
phase_rad(A < 1e-6) = 0;    % 幅值接近0时相位置0，避免无意义的相位值
phase_deg = rad2deg(phase_rad); % 相位转换为角度 [°]
f_half = f(1:N_fft/2+1);    % 单边频率轴（0~Fs/2，符合实际分析需求）

%% ===================== 6. 提取各次谐波的幅值、相位、频率 =====================
% 结构体存储谐波结果，方便后续调用
harmonic = struct('order', [], 'freq', [], 'amplitude', [], 'phase_deg', []);
for k = 1:harmonic_order
    f_k = k * f0;           % 第k次谐波的理论频率
    [~, idx] = min(abs(f_half - f_k)); % 匹配FFT离散频率轴中最接近的点
    harmonic.order(k) = k;
    harmonic.freq(k) = f_half(idx);    % 实际匹配的频率
    harmonic.amplitude(k) = A(idx);    % 谐波幅值（与Excel数据单位一致：V/A）
    harmonic.phase_deg(k) = phase_deg(idx); % 谐波相位（°）
end

%% ===================== 7. 结果控制台输出（清晰表格形式，MATLAB原生语法）=====================
fprintf('===================== %s 谐波分析结果 =====================\n', sig_name);
fprintf('采样频率：%d Hz | 基波频率：%d Hz | 最高分析谐波：%d次\n', Fs, f0, harmonic_order);
fprintf('读取起始行：%d | 有效采样点数：%d | 分析周期数：%d个基波周期\n\n', start_row, N_fft, n_cycle);
fprintf('次谐波\t理论频率(Hz)\t实际频率(Hz)\t幅值\t\t相位(°)\n');
fprintf('--------------------------------------------------------\n');
for k = 1:harmonic_order
    fprintf('%d\t\t%.2f\t\t%.2f\t\t%.4f\t\t%.2f\n', ...
        harmonic.order(k), k*f0, harmonic.freq(k), ...
        harmonic.amplitude(k), harmonic.phase_deg(k));
end

%% ===================== 8. 总谐波畸变率 THD 计算（谐波分析关键指标，可选）=====================
A1 = harmonic.amplitude(1); % 基波幅值
if A1 < 1e-6
    warning('基波幅值接近0，THD计算无意义！');
else
    A_harm = harmonic.amplitude(2:end); % 2次及以上谐波幅值
    THD = sqrt(sum(A_harm.^2)) / A1 * 100; % THD计算公式（%）
    fprintf('\n%s总谐波畸变率 THD = %.2f %% \n', sig_name, THD);
end

%% ===================== 9. 结果可视化（原始波形+FFT频谱，直观展示）=====================
figure('Color','w','Position',[100,100,1200,600]); % 白色背景，指定窗口大小
% 子图1：截取后的整数周期原始波形
subplot(1,2,1);
t = (0:N_fft-1)/Fs; % 时间轴 [s]
plot(t, sig_fft, 'b-', 'LineWidth',1.2);
xlabel('时间 t (s)');
ylabel([sig_name, ' (', unit, ')']); % 拼接单位，MATLAB原生写法
title([num2str(n_cycle), '个基波周期的', sig_name, '波形']);
grid on; grid minor; % 显示网格，方便观察

% 子图2：FFT单边频谱图（标注各次谐波点）
subplot(1,2,2);
plot(f_half, A, 'b-', 'LineWidth',1.2);
hold on;
plot(harmonic.freq, harmonic.amplitude, 'ro', 'MarkerSize',6, 'DisplayName','各次谐波');
xlabel('频率 f (Hz)');
ylabel(['幅值 (', unit, ')']);
title([sig_name, ' FFT频谱（基波', num2str(f0), 'Hz）']);
xlim([0, (harmonic_order+1)*f0]); % 横坐标限定到最高次谐波，避免冗余
grid on; grid minor;
legend('Location','best');
hold off;

%% 可选：将谐波结果写入新Excel（含起始行/采样频率等参数，方便后续分析）
% result = [harmonic.order', harmonic.freq', harmonic.amplitude', harmonic.phase_deg'];
% writematrix(result, '谐波分析结果.xlsx', 'Sheet',1, 'Range','A1');
% writematrix([Fs, f0, start_row, THD], '谐波分析结果.xlsx', 'Sheet',2, 'Range','A1');