1. 研究背景
- 核心问题 :传统BP神经网络在回归预测任务中,其性能高度依赖于网络结构 (如隐藏层节点数)和初始权重与阈值(易陷入局部最优)。
- 现有方案的不足 :
- 结构参数(如隐藏层节点数、学习率)通常依赖经验试错,效率低且难以保证最优。
- 初始权重随机生成,容易导致模型收敛到次优解。
- 解决方案 :提出一种双层优化框架 ,将贝叶斯优化 与改进的麻雀搜索算法相结合,实现结构参数与初始权重的自动、全局寻优,旨在提升模型的预测精度与泛化能力。
2. 主要功能
- 核心功能 :实现一个多输入单输出的回归预测模型。
- 主要流程 :
- 数据预处理:读取数据、归一化、划分训练/测试集。
- 第一层优化(贝叶斯优化):自动搜索BP神经网络的最佳隐藏层节点数和学习率。
- 第二层优化(ISSA):使用改进的麻雀搜索算法优化BP网络第一层优化所得的初始权重和阈值。
- 模型训练与评估:使用优化后的结构和权重训练BP网络,并评估其在训练集和测试集上的性能(RMSE, MAE, R²)。
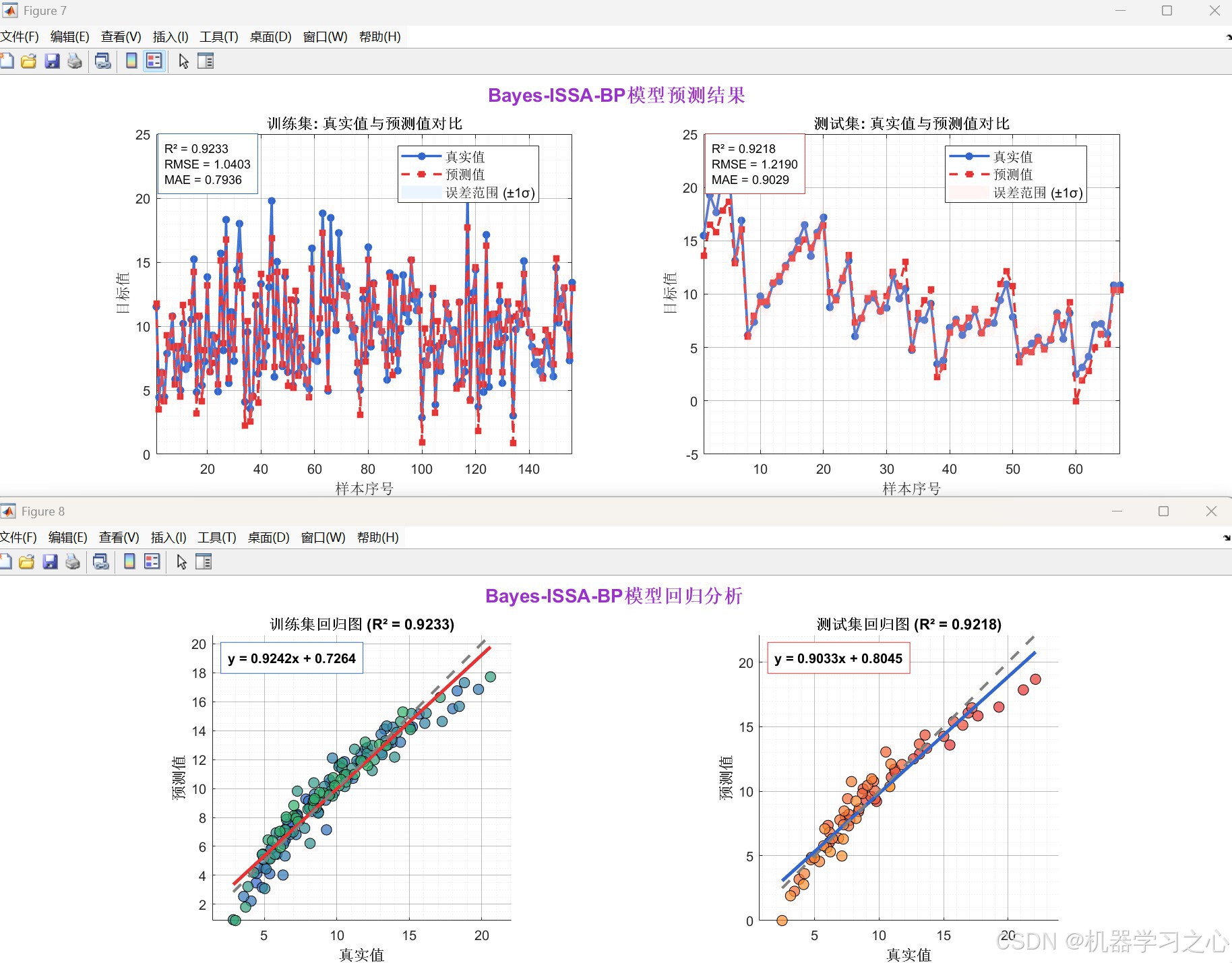
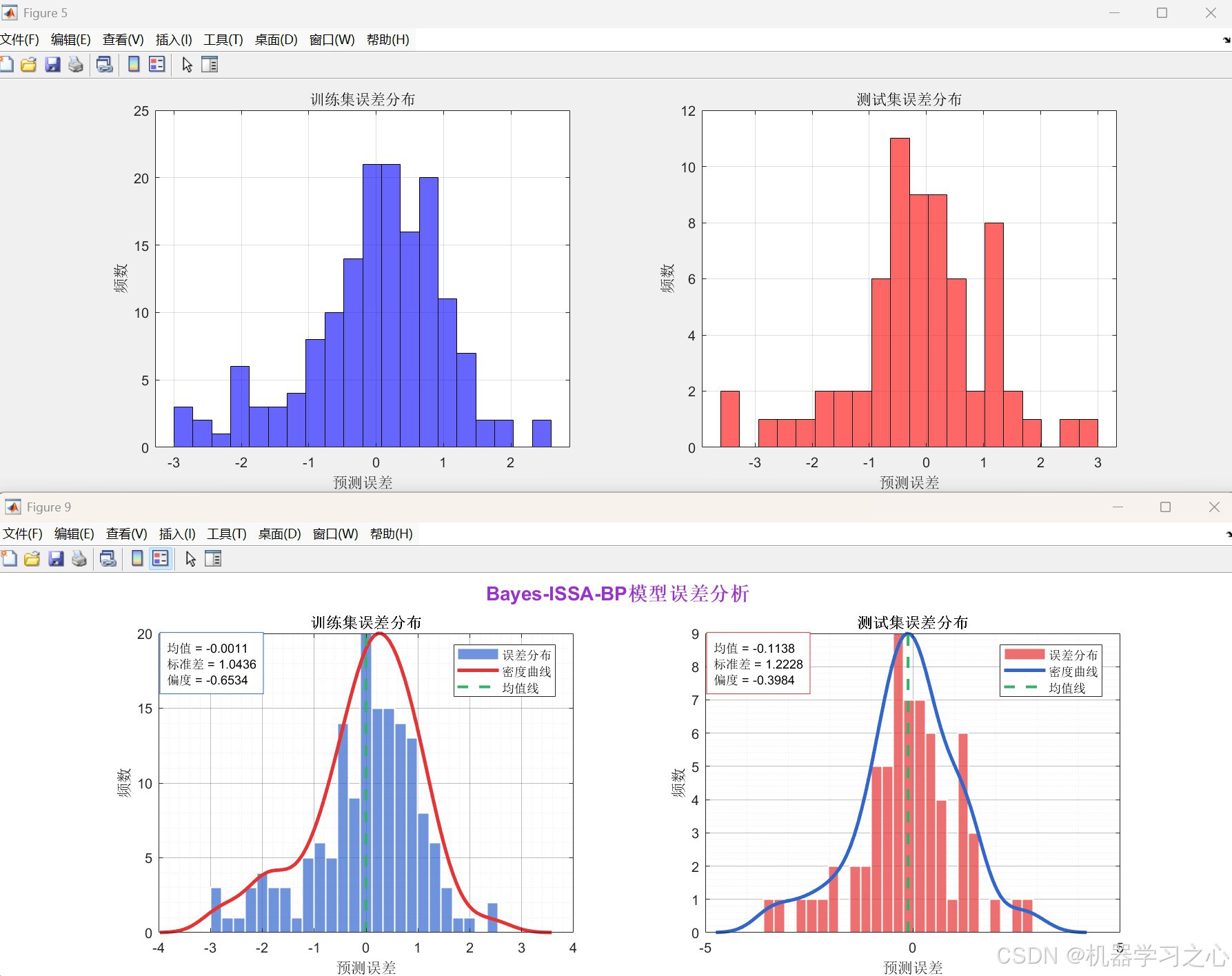
- 结果可视化:生成预测对比图、回归图、误差分布图、收敛曲线等。
3. 算法步骤
- 数据准备:数据归一化,按7:3划分训练集和测试集。
- 贝叶斯优化层 :
- 目标函数:以网络在验证集上的RMSE为优化目标。
- 优化变量:隐藏层节点数(整数)、学习率(对数尺度)。
- 输出 :一组最优的
(hiddenSize, learnRate)。
- ISSA优化层 :
- 编码:将BP网络的所有权重和阈值编码为一个长向量。
- 初始化:使用Tent混沌映射初始化麻雀种群。
- 迭代优化:按照麻雀的发现者-跟随者-侦察者模型更新位置,融入莱维飞行、自适应权重等改进策略。
- 适应度计算:以网络在训练集上的RMSE作为适应度。
- 输出:一组最优的权重向量。
- BP网络训练:使用ISSA优化的权重作为初始值,采用反向传播进行微调训练。
- 预测与评估:在测试集上进行预测,计算多个性能指标。
4. 技术路线
- 上层(宏观参数) :
贝叶斯优化 (Bayesian Optimization)→ 确定网络结构参数。 - 下层(微观参数) :
改进麻雀算法 (ISSA)→ 优化网络初始权重/阈值。 - 底层模型 :
BP神经网络 (Back Propagation Neural Network)→ 执行最终回归预测。 - 整体架构:形成"贝叶斯优化指导ISSA,ISSA优化BP"的串行双层优化流水线。
5. 关键原理
- 自适应权重 :
w = w_max - (w_max - w_min) * (current_iter / max_iter)^2,实现非线性递减,平衡探索与开发。 - 莱维飞行 :
L = 0.01 * step; step = u ./ (abs(v).^(1/beta)),生成长步长的随机游走,增强全局探索能力。 - Tent混沌映射 :
x(i) = 2 * x(i-1) (if x(i-1)<0.5) else 2*(1-x(i-1)),用于种群初始化,增加多样性。 - 网络前向传播 :
A1 = tansig(W1*X + B1); A2 = W2*A1 + B2(线性输出层)。 - 误差反向传播 :基于梯度下降法更新权重
W和偏置B。
6. 关键参数设定
- 贝叶斯优化 :
hiddenSize: [5, 50] (整数)learnRate: [0.001, 0.1] (对数变换)MaxObjectiveEvaluations: 30 (主程序中为加速测试设为5)
- ISSA优化 :
pop_size: 10 (主程序中为加速测试设置)max_iter: 20 (主程序中为加速测试设置)PD(发现者比例): 0.7SD(侦察者比例): 0.2ST(安全阈值): 0.6
- BP网络训练 :
max_epochs: 500goal: 1e-5 (MSE)
7. 运行环境
- 平台:MATLAB (推荐R2020a或更高版本)。
8. 应用场景
- 通用领域 :任何需要建立多变量输入到单一连续目标值映射关系的回归预测问题。
- 典型示例 :
- 工业控制:根据生产工艺参数(温度、压力、流量等)预测产品质量指标。
- 金融预测:根据宏观经济指标预测股票指数或汇率。
- 能源领域:根据天气、历史负荷预测电力负荷。
- 科学实验:根据实验条件预测物理或化学反应的结果。
- 优势 :特别适用于数据量有限、变量间关系复杂、传统模型调参困难的场景。其双层优化机制能有效提升小样本下的模型性能和稳定性。
总结 :该"Bayes-ISSA-BP"模型是一个结构精巧、自动化程度高 的智能回归预测框架。它通过贝叶斯优化 和改进元启发式算法 的双重机制,系统性地解决了神经网络结构设计 和参数初始化两大难题,旨在以更少的先验知识获得预测性能更优、泛化能力更强的模型,具有良好的研究价值和工程应用前景。
matlab
========== 数据读取与预处理 ==========
数据读取完成! 输入维度: 5, 输出维度: 1
训练样本数: 156, 测试样本数: 67
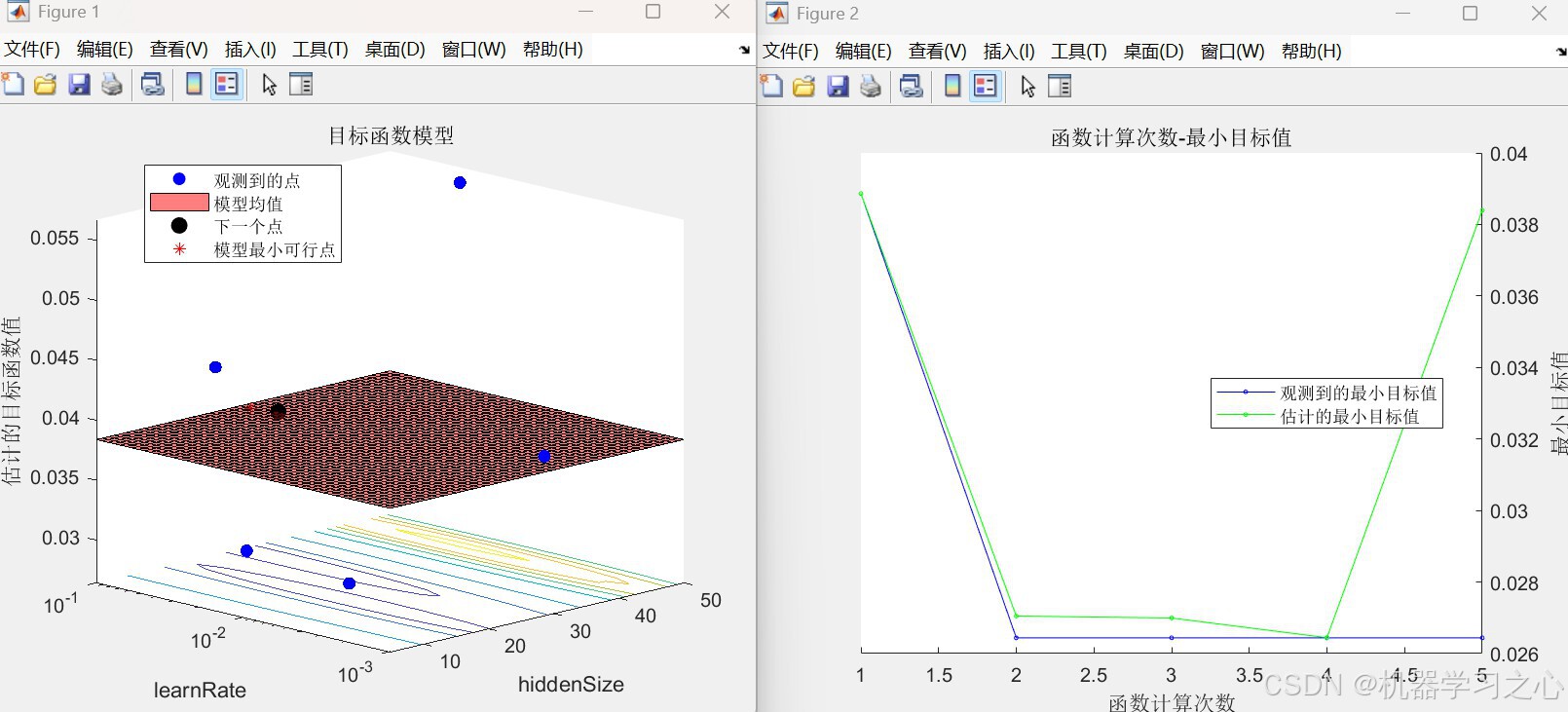
========== 第一层优化: 贝叶斯优化 ==========
|=====================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | hiddenSize | learnRate |
| | result | | runtime | (observed) | (estim.) | | |
|=====================================================================================================|
| 1 | Best | 0.038863 | 0.22308 | 0.038863 | 0.038863 | 32 | 0.0014119 |
| 2 | Best | 0.02644 | 0.10029 | 0.02644 | 0.027049 | 27 | 0.089957 |
| 3 | Accept | 0.02776 | 0.10571 | 0.02644 | 0.026994 | 19 | 0.0079474 |
| 4 | Accept | 0.05674 | 0.10505 | 0.02644 | 0.026444 | 45 | 0.020045 |
| 5 | Accept | 0.042171 | 0.11619 | 0.02644 | 0.038395 | 23 | 0.097583 |
__________________________________________________________
优化完成。
达到 MaxObjectiveEvaluations 5。
函数计算总次数: 5
总历时: 3.8435 秒
总目标函数计算时间: 0.65032
观测到的最佳可行点:
hiddenSize learnRate
__________ _________
27 0.089957
观测到的目标函数值 = 0.02644
估计的目标函数值 = 0.038395
函数计算时间 = 0.10029
估计的最佳可行点(根据模型):
hiddenSize learnRate
__________ _________
27 0.089957
估计的目标函数值 = 0.038395
估计的函数计算时间 = 0.1084
贝叶斯优化完成!
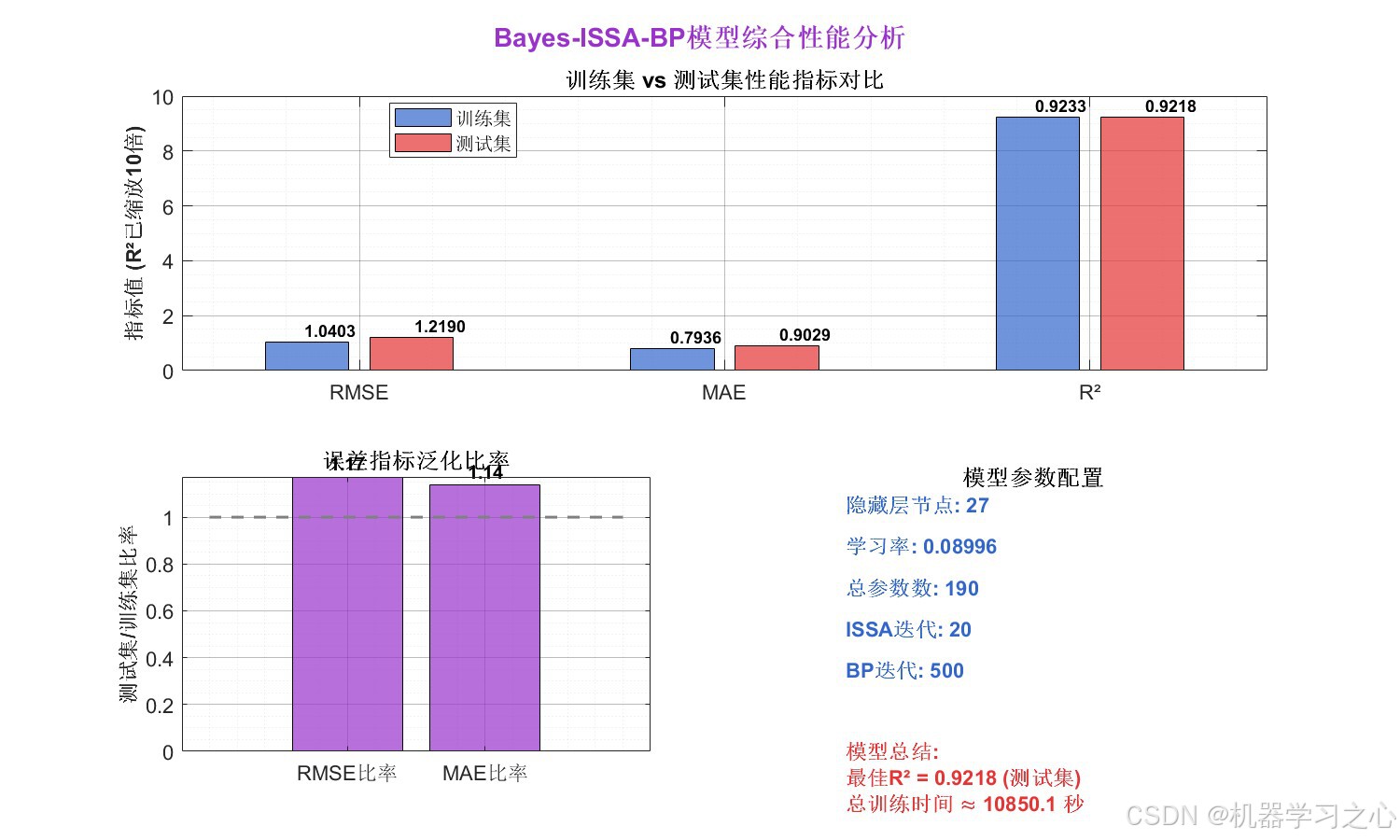
最佳隐藏层节点数: 27
最佳学习率: 0.089957
========== 第二层优化: 改进麻雀算法 ==========
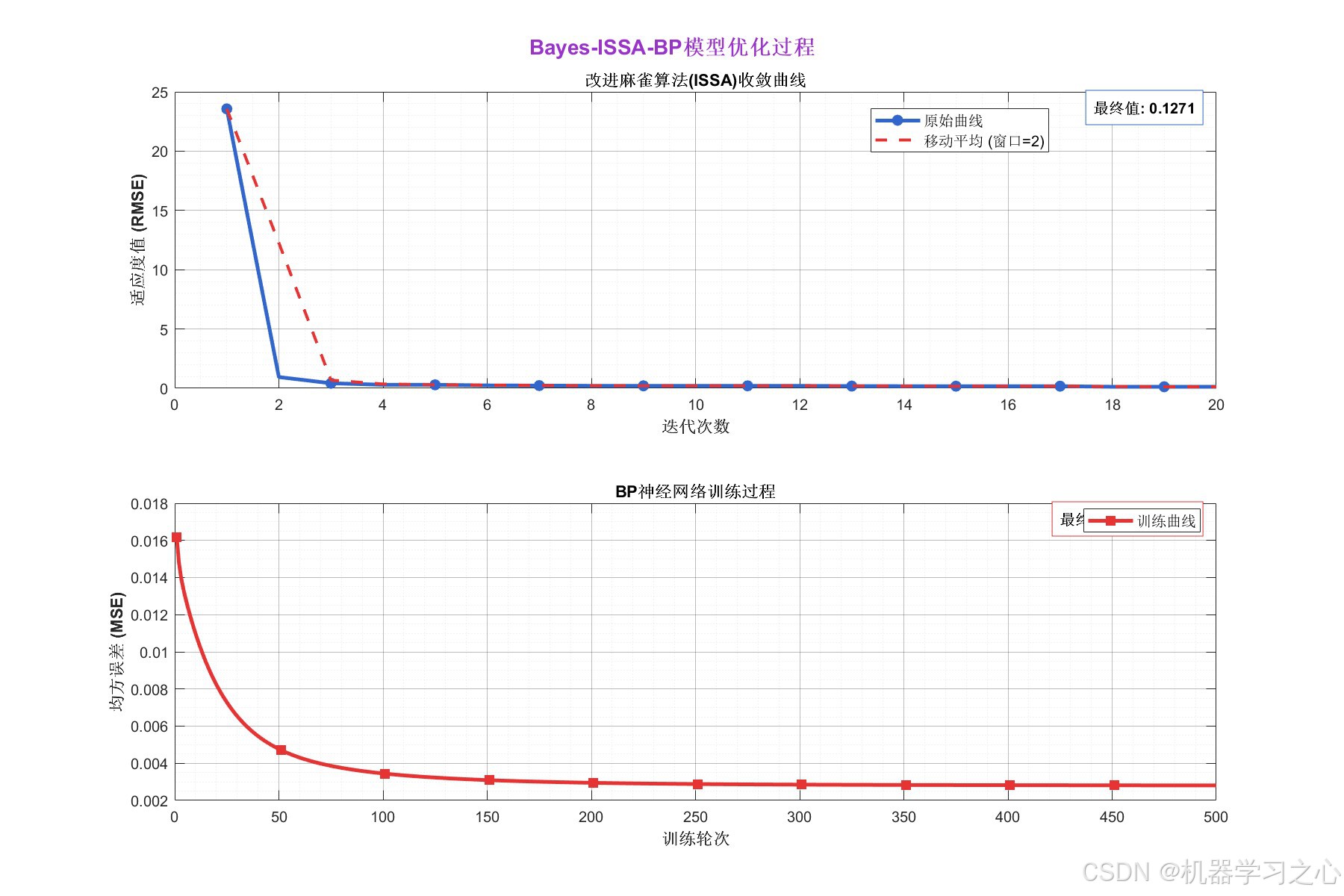
迭代 5/20,最佳适应度: 0.29222
迭代 10/20,最佳适应度: 0.20518
迭代 15/20,最佳适应度: 0.17606
迭代 20/20,最佳适应度: 0.12713
改进麻雀算法优化完成!
最佳适应度值: 0.12713
========== 构建和训练BP神经网络 ==========
Epoch 100, MSE: 0.003453
Epoch 200, MSE: 0.002950
Epoch 300, MSE: 0.002850
Epoch 400, MSE: 0.002821
Epoch 500, MSE: 0.002807
========== 模型测试与评估 ==========
========== 性能指标 ==========
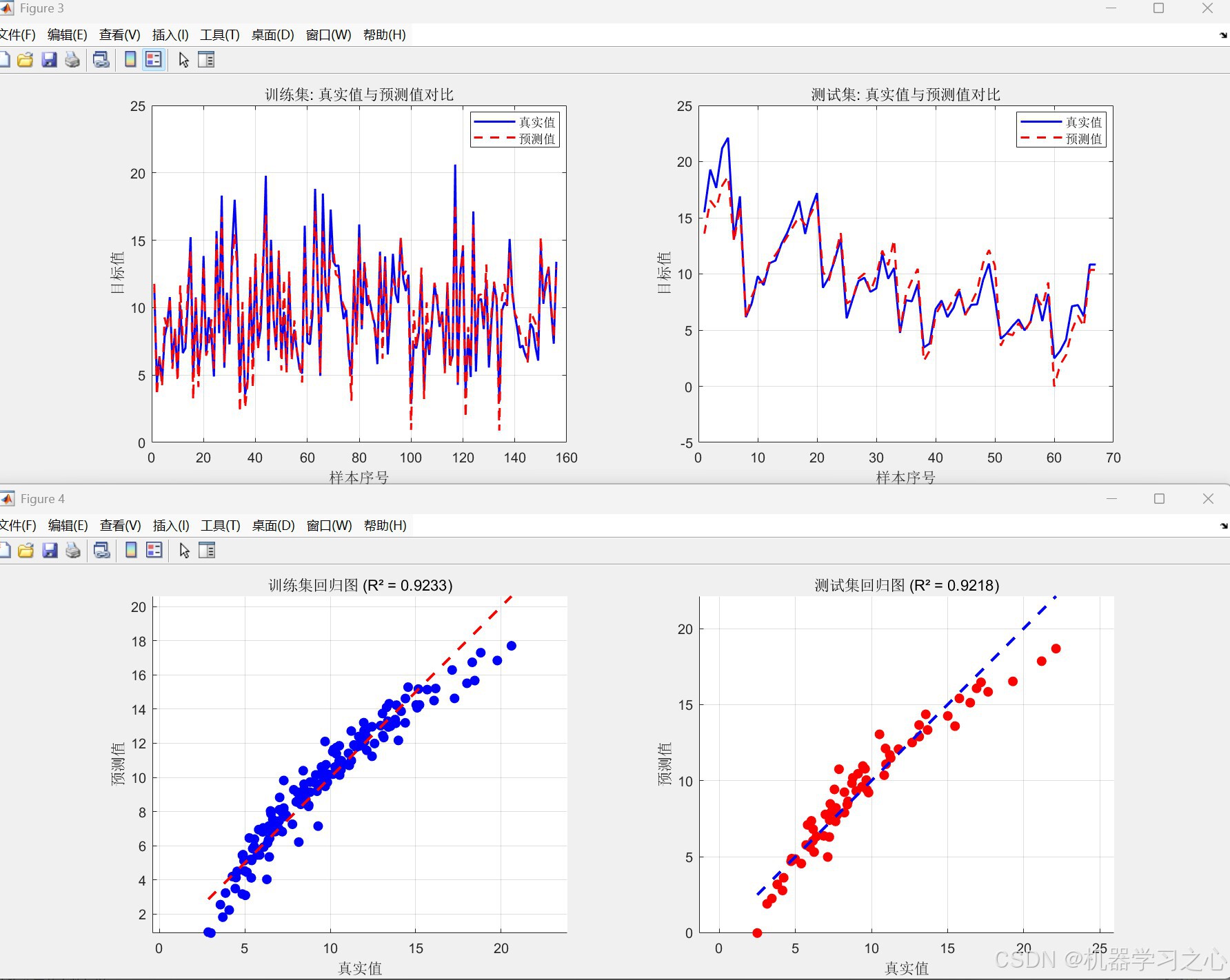
训练集:
RMSE: 1.0403
MAE: 0.7936
R²: 0.92332
测试集:
RMSE: 1.219
MAE: 0.90285
R²: 0.92178
========== 生成可视化结果 ==========
========== Bayes-ISSA-BP模型训练完成 ==========
========== 生成可视化结果 ==========
========== 可视化结果已生成 ==========
>>