NumPy 和 Pandas 中常用的数组/张量操作方法
python
# shape属性
import numpy as np
arr = np.array([[1, 2, 3],[4, 5, 6]])
print(arr.shape) # 输出:(2, 3) → 2行3列 返回值:一个元组,每个元素表示对应维度的长度
# reshape()方法
arr = np.arange(6) # [0, 1, 2, 3, 4, 5]
print(arr.reshape(2, 3))
# 输出: 改变数组形状(重新排列数据),不改变数据本身,返回新视图(如果可能)
# [[0 1 2]
# [3 4 5]]
# 自动计算维度
print(arr.reshape(3, -1)) # 3行,列数自动计算为2
# astype() 方法
arr = np.array([1.5, 2.7, 3.1])
print(arr.astype(int)) # 输出:[1 2 3](截断小数)
# 转换数据类型以节省内存
arr_float64 = np.array([1, 2, 3], dtype=np.float64)
arr_float32 = arr_float64.astype(np.float32)
print(arr_float32.dtype) # 输出:float32标量(0D张量)
仅包含一个数字的张量叫作标量(scalar,也叫标量张量、零维张量、0D 张量)。
在 Numpy中,一个 float32 或 float64 的数字就是一个标量张量(或标量数组)。
用 ndim 属性来查看一个 Numpy 张量的轴的个数,标量张量有 0 个轴(ndim == 0),张量轴的个数也叫作阶(rank)
python
import numpy as np
x = np.array(12) # array(12)
x.ndim # 0向量(1D张量)
数字组成的数组叫作向量(vector)或一维张量(1D 张量),一维张量只有一个轴。
python
x = np.array([12, 3, 6, 14, 7]) # array([12, 3, 6, 14, 7])
x.ndim # 1矩阵(2D张量)
向量组成的数组叫作矩阵(matrix)或二维张量(2D 张量),矩阵有 2 个轴(通常叫作行和列)
第一个轴上的元素叫作行(row),第二个轴上的元素叫作列(column)。
python
x = np.arrah([
[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]
])
x.ndim # 2向量数据:2D张量,形状为(samples,features)
①、人口统计数据集,其中包括每个人的年龄、邮编和收入。每个人可以表示为包含 3 个值
的向量,而整个数据集包含 100 000 个人,因此可以存储在形状为 (100000, 3) 的 2D
张量中
②、文本文档数据集,我们将每个文档表示为每个单词在其中出现的次数(字典中包含
20 000 个常见单词)。每个文档可以被编码为包含 20 000 个值的向量(每个值对应于
字典中每个单词的出现次数),整个数据集包含 500 个文档,因此可以存储在形状为
(500, 20000) 的张量中
3D 张量与更高维张量
将多个矩阵组合成一个新的数组,可以得到一个 3D 张量
python
x = np.array([
[
[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]
],
[
[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]
],
[
[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]
]
])
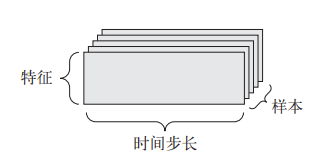
x.ndim # 3时间序列数据或序列数据:3D 张量,形状为 (samples, timesteps, features)
①、股票价格数据集。每一分钟,我们将股票的当前价格、前一分钟的最高价格和前一分钟
的最低价格保存下来。因此每分钟被编码为一个 3D 向量,整个交易日被编码为一个形
状为 (390, 3) 的 2D 张量(一个交易日有 390 分钟),而 250 天的数据则可以保存在一
个形状为 (250, 390, 3) 的 3D 张量中。这里每个样本是一天的股票数据。
②、推文数据集。我们将每条推文编码为 280 个字符组成的序列,而每个字符又来自于 128
个字符组成的字母表。在这种情况下,每个字符可以被编码为大小为 128 的二进制向量
(只有在该字符对应的索引位置取值为 1,其他元素都为 0)。那么每条推文可以被编码
为一个形状为 (280, 128) 的 2D 张量,而包含 100 万条推文的数据集则可以存储在一
个形状为 (1000000, 280, 128) 的张量中
关键属性:
- 轴的个数(阶),3D 张量有 3 个轴,在 Numpy 等 Python 库中也叫张量的 ndim
- 形状:整数元组,表示张量沿每个轴的维度大小(元素个数)
上述的:2D矩阵,形状为(3,5) | 3D张量形状为(3,3,5) | 向量的形状只包含一个元素,比如 (5,) | 而标量的形状为空,即 ()。 - 数据类型,在 Python 库中通常叫作 dtype,张量的类型可以是 float32、uint8、float64 等
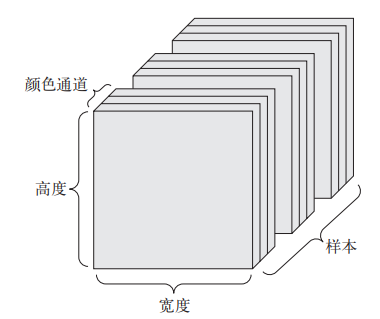
图像 :4D 张量,形状为 (samples, height, width, channels) 或 (samples, channels,
height, width)
①、图像通常具有三个维度:高度、宽度和颜色深度
虽然灰度图像(比如 MNIST 数字图像)只有一个颜色通道,因此可以保存在 2D 张量中,但按照惯例,图像张量始终都是 3D 张量,灰
度图像的彩色通道只有一维,因此,如果图像大小为 256×256,那么 128 张灰度图像组成的批量可以保存在一个形状为 (128, 256, 256, 1) 的张量中
而 128 张彩色图像组成的批量则可以保存在一个形状为 (128, 256, 256, 3) 的张量中
图像张量的形状有两种约定(Keras 框架同时支持这两种格式)
- 通道在后(channels-last)的约定(在 TensorFlow 中使用),Google 的 TensorFlow 机器学习框架将
颜色深度轴放在最后:(samples, height, width, color_depth) - 通道在前(channels-first)的约定(在 Theano 中使用),Theano将图像深度轴放在批量轴之后:(samples, color_depth, height, width)。,前面的两个例子将变成 (128, 1, 256, 256) 和 (128, 3, 256, 256)
视频 :5D 张量,形状为 (samples, frames, height, width, channels) 或 (samples,
frames, channels, height, width)
视频可以看作一系列帧,每一帧都是一张彩色图像。
由于每一帧都可以保存在一个形状为 (height, width, color_depth) 的 3D 张量中,因此一系列帧可以保存在一个形状为 (frames, height, width, color_depth) 的 4D 张量中
而不同视频组成的批量则可以保存在一个 5D 张量中,其形状为(samples, frames, height, width, color_depth)
一个以每秒 4 帧采样的 60 秒 YouTube 视频片段,视频尺寸为 144×256,这个视频共有 240 帧。4 个这样的视频片段组成的批量将保存在形状为 (4, 240, 144, 256, 3)的张量中。总共有 106 168 320 个值
如果张量的数据类型(dtype)是 float32,每个值都是32 位,那么这个张量共有 405MB,现实生活中遇到的视频要小得多,因为它们不以float32 格式存储,而且通常被大大压缩,比如 MPEG 格式
张量运算
python
# 库中封装后的张量逐元素运算
import numpy as np
z = x + y #逐元素的相加
z = np.maximum(z, 0.) # 逐元素的relu 注意浮点数0. 逐元素比较两个数组,取对应位置的最大值形状不同的张量相加
- 较小的张量会被广播(broadcast),以匹配较大张量的形状
- 向较小的张量添加轴(叫作广播轴),使其 ndim 与较大的张量相同
- 将较小的张量沿着新轴重复,使其形状与较大的张量相同
python
import numpy as np
x = np.random.random((64, 3, 32, 10)) # x 是形状为 (64, 3, 32, 10) 的随机张量
y = np.random.random((32, 10)) # y 是形状为 (32, 10) 的随机张量
z = np.maximum(x,y) # 输出 z 的形状是 (64, 3, 32, 10),与 x 相同 张量点积
点积运算,也叫张量积(tensor product,不要与逐元素的乘积弄混),与逐元素的运算不同,它将输入张量的元素合并在一起
- 在 Numpy、Keras、Theano 和 TensorFlow 中,都是用 * 实现逐元素乘积
- TensorFlow 中的点积使用了不同的语法,但在 Numpy 和 Keras 中,都是用标准的 dot 运算符来实现点积
python
import numpy as np
z = np.dot(x,y) # 数学符号中的点(.)表示点积运算 z=x.y两个向量之间的点积是一个标量,而且只有元素个数相同的向量之间才能做点积 z += x[i] * y[i]
python
def naive_vector_dot(x, y):
assert len(x.shape) == 1
assert len(y.shape) == 1
assert x.shape[0] == y.shape[0]
z = 0.
for i in range(x.shape[0]):
z += x[i] * y[i]
return z对一个矩阵 x 和一个向量 y 做点积,返回值是一个向量,其中每个元素是 y 和 x的每一行之间的点积。
python
import numpy as np
def naive_matrix_vector_dot(x, y):
assert len(x.shape) == 2
assert len(y.shape) == 1
assert x.shape[1] == y.shape[0] # x 的第 1 维和 y 的第 0 维大小必须相同
z = np.zeros(x.shape[0])
for i in range(x.shape[0]):
for j in range(x.shape[1]):
z[i] += x[i, j] * y[j]
return z对于两个矩阵 x 和 y,当且仅当 x.shape[1] == y.shape[0] 时,你才可以对它们做点积(dot(x, y))。得到的结果是一个形状为(x.shape[0], y.shape[1]) 的矩阵,其元素为 x的行与 y 的列之间的点积。
python
def naive_matrix_dot(x, y):
assert len(x.shape) == 2
assert len(y.shape) == 2
assert x.shape[1] == y.shape[0]
z = np.zeros((x.shape[0], y.shape[1]))
for i in range(x.shape[0]):
for j in range(y.shape[1]):
row_x = x[i, :]
column_y = y[:, j]
z[i, j] = naive_vector_dot(row_x, column_y)
return z张量变形
张量变形是指改变张量的行和列,以得到想要的形状。变形后的张量的元素总个数与初始张量相同
python
x = np.array([
[0., 1.],
[2., 3.],
[4., 5.]
])
print(x.shape) # (3,2)
x = x.reshape((6,1))
"""
array([[ 0.],
[ 1.],
[ 2.],
[ 3.],
[ 4.],
[ 5.]])
"""
x = x.reshape((2, 3))
"""
array([[ 0., 1., 2.],
[ 3., 4., 5.]])
"""
# 转置,对矩阵的行和列互换
x = np.zeros((300, 20))
x = np.transpose(x)
print(x.shape) # (20, 300)