数组双指针部分指南:快慢·左右·倒序与避坑清单
双指针是数组/链表题里的「解题神器」:通过指针分工实现一次遍历、原地修改 。本文数组覆盖 3 类核心模板 (快慢指针、左右指针、倒序双指针)和 2 类进阶(中心扩展、三指针分区),并标清指针语义、循环条件与等于号取舍,方便直接套题。
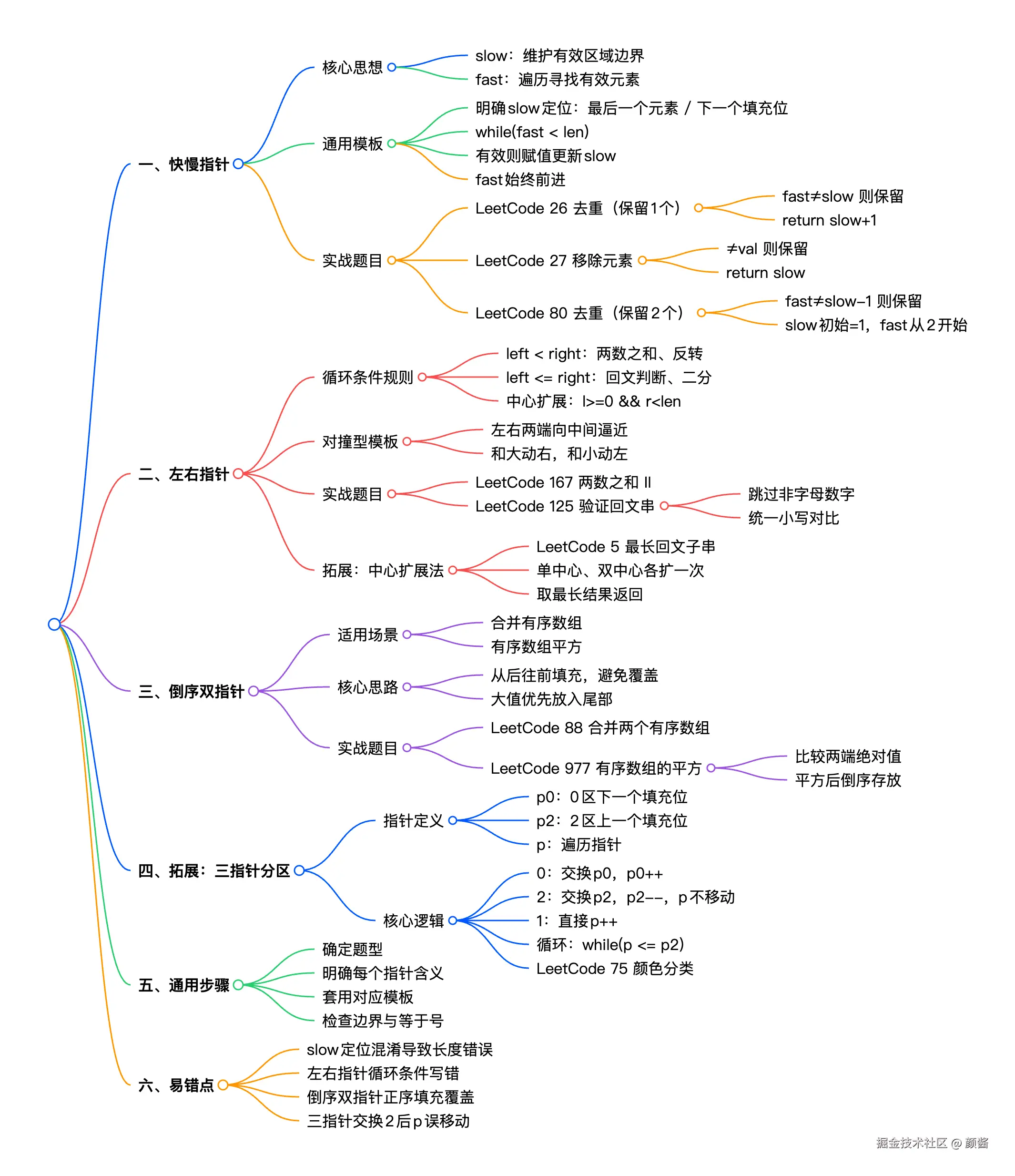
一、快慢指针模板(核心:原地修改/去重)
模板核心定义(必须记死)
| 指针 | 定位(二选一,标注清楚!) | 示例场景 |
|---|---|---|
| slow | 已保留区域的最后一个元素索引 | 有序数组去重(LeetCode 26) |
| slow | 新区域的下一个要填充的位置 | 移除指定元素(LeetCode 27) |
| fast | 遍历指针,探索所有元素(固定) | 所有快慢指针场景 |
通用模板(适配 90% 快慢指针题)
JavaScript
/**
* 快慢指针通用模板
* @param {Array} arr - 待处理数组
* @param {Function} isValid - 判定fast指向元素是否有效(需保留)
* @return {number} - 新数组长度
*/
function slowFastPointerTemplate(arr, isValid) {
const len = arr.length;
if (len <= 1) return len; // 边界:空/单元素直接返回
// === 关键:明确slow的初始定位 ===
let slow = 0; // 示例:已保留区域最后一个元素(初始在第一个元素)
// let slow = 0; // 示例:新区域下一个要填充的位置(初始在第一个位置)
let fast = 0;
while (fast < len) {
// 核心:fast找到有效元素
if (isValid(arr[fast], arr[slow], slow)) {
// === 关键:根据slow定位调整 ===
slow++; // 若slow是「已保留最后一个」→ 先移动再赋值
// 若slow是「下一个填充位」→ 直接赋值(无需先移动)
arr[slow] = arr[fast];
}
fast++; // 无论是否有效,fast始终遍历
}
// === 长度计算规则 ===
// 1. slow是「已保留最后一个索引」→ 返回 slow + 1
// 2. slow是「下一个填充位」→ 返回 slow
return slow + 1;
}模板实战1:有序数组去重(保留1个,LeetCode 26)
题目描述:给你一个非严格递增排列的数组 nums ,请你原地删除重复出现的元素,使每个元素只出现一次,返回删除后数组的新长度。元素的相对顺序应该保持一致。要求:更改数组 nums ,使 nums 的前 k 个元素包含唯一元素,并按照它们最初在 nums 中出现的顺序排列;nums 的其余元素与 nums 的大小不重要,最终返回 k 。
解题思路:
-
核心适配:沿用快慢指针模板,明确指针定位------slow 为「已保留区域的最后一个元素索引」,fast 为遍历指针,负责探索所有元素。
-
有效判断:当 fast 指向元素与 slow 指向元素不同时,说明该元素是新的有效元素(未重复)。
-
指针操作:找到有效元素后,先将 slow 移动到下一个填充位,再将 fast 元素赋值给 slow。
-
长度返回:因 slow 是最后一个有效元素的索引,最终返回 slow + 1 即为新数组长度。
JavaScript
var removeDuplicates = function(nums) {
const len = nums.length;
if (len <= 1) return len;
// slow:已保留区域的最后一个元素索引(初始在0)
let slow = 0;
let fast = 0;
while (fast < len) {
// 有效条件:fast元素 ≠ slow元素(新元素)
if (nums[fast] !== nums[slow]) {
slow++; // 先移动到下一个填充位
nums[slow] = nums[fast];
}
fast++;
}
return slow + 1; // slow是最后一个有效索引 → +1
};模板实战2:移除指定元素(LeetCode 27)
题目描述:给你一个数组 nums 和一个值 val,你需要原地移除所有数值等于 val 的元素,元素的顺序可能发生改变,然后返回 nums 中与 val 不同的元素的数量。要求:不能使用额外的数组空间,必须原地修改输入数组并使用 O(1) 额外空间完成。
解题思路:
-
指针定位:调整 slow 定位为「新区域的下一个要填充的位置」,fast 仍为遍历指针,筛选不等于 val 的有效元素。
-
有效判断:当 fast 指向元素不等于 val 时,该元素需保留,直接填充到 slow 指向的位置。
-
指针操作:填充完成后,将 slow 移动到下一个填充位,fast 继续遍历下一个元素。
-
长度返回:slow 本身指向新区域的下一个填充位,其值即为有效元素的数量,直接返回 slow 即可。
JavaScript
var removeElement = function(nums, val) {
const len = nums.length;
if (len === 0) return 0;
// slow:新区域的「下一个要填充的位置」(初始在0)
let slow = 0;
let fast = 0;
while (fast < len) {
// 有效条件:fast元素 ≠ 目标值
if (nums[fast] !== val) {
nums[slow] = nums[fast]; // 直接赋值(slow是填充位)
slow++; // 填充后移动到下一个位置
}
fast++;
}
return slow; // slow是下一个填充位 → 直接返回
};模板实战3:有序数组去重(保留2个,LeetCode 80)
题目描述:给你一个有序数组 nums ,请你原地删除重复出现的元素,使得出现次数超过两次的元素只出现两次,返回删除后数组的新长度。要求:不要使用额外的数组空间,必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。
解题思路:
-
模板优化:基于快慢指针模板,slow 仍为「已保留区域的最后一个元素索引」,结合有序数组重复元素连续的特性调整逻辑。
-
初始定位:因最多保留2个重复元素,前两个元素默认有效,slow 初始设为1,fast 从第三个元素(索引2)开始探索。
-
有效判断:当 fast 元素与 slow-1 元素不同时,说明该元素最多出现两次,可保留(避免出现3个及以上重复)。
-
指针与返回:符合条件则移动 slow 并赋值,最终 slow 为最后一个有效元素索引,返回 slow + 1 即为新长度。
JavaScript
var removeDuplicates = function(nums) {
const len = nums.length;
if (len <= 2) return len;
// slow:已保留区域的最后一个元素索引(初始在1,前两个元素默认保留)
let slow = 1;
let fast = 2;
while (fast < len) {
// 有效条件:fast元素 ≠ slow-1元素(保证最多保留2个)
if (nums[fast] !== nums[slow - 1]) {
slow++;
nums[slow] = nums[fast];
}
fast++;
}
return slow + 1;
};二、左右指针模板(核心:对撞/扩散)
模板核心规则(循环条件等于号取舍)
| 场景 | while条件 | 等于号取舍原因 |
|---|---|---|
| 两数之和/反转数组 | left < right | 指针相遇时无需处理(单个元素无意义) |
| 二分查找/回文串判断(全字符) | left <= right | 需处理单个元素(如奇数长度回文中心) |
| 中心扩展(回文子串) | left >= 0 && right < len | 越界即停止,无等于号 |
通用模板1:对撞型左右指针(两数之和/反转)
JavaScript
/**
* 对撞型左右指针模板
* @param {Array} arr - 有序数组
* @param {Function} condition - 指针移动条件
* @return {any} - 解题结果
*/
function leftRightCollideTemplate(arr, condition) {
let left = 0;
let right = arr.length - 1;
let res = null;
// === 关键:根据场景选条件 ===
while (left < right) { // 无等于号:两数之和/反转
// while (left <= right) { // 有等于号:二分查找/全字符回文判断
const cur = condition(arr[left], arr[right], left, right);
if (cur === 'moveLeft') {
left++;
} else if (cur === 'moveRight') {
right--;
} else if (cur === 'found') {
res = [left, right];
break;
}
}
return res;
}模板实战1:两数之和 II(LeetCode 167)
题目描述:给你一个下标从 1 开始的整数数组 numbers ,该数组已按非递减顺序排列,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。要求:每个输入只对应唯一的答案,不可以重复使用相同的元素,解决方案必须只使用常量级的额外空间。
解题思路:
-
模板适配:套用对撞型左右指针模板,利用数组非递减有序的特性,实现高效查找。
-
指针定位:left 从数组头部(索引0)开始,right 从数组尾部(索引length-1)开始,相向对撞遍历。
-
循环条件:用 left < right,因两数需不同元素,指针相遇时无需处理(单个元素无法组成两个数)。
-
指针操作:计算两指针元素之和,和等于 target 则返回下标+1(题目要求下标从1开始);和大于 target 则右指针左移(减小和);和小于 target 则左指针右移(增大和)。
JavaScript
var twoSum = function(numbers, target) {
let left = 0;
let right = numbers.length - 1;
// 无等于号:两数不能是同一个元素
while (left < right) {
const sum = numbers[left] + numbers[right];
if (sum === target) {
return [left + 1, right + 1]; // 题目下标从1开始
} else if (sum > target) {
right--; // 和太大,右指针左移
} else {
left++; // 和太小,左指针右移
}
}
return [-1, -1];
};模板实战2:验证回文串(LeetCode 125)
题目描述:如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样,则可以认为该短语是一个回文串。字母和数字都属于字母数字字符。给你一个字符串 s ,请你判断它是否是一个回文串。
解题思路:
-
模板适配:使用对撞型左右指针,核心是对比字符串首尾对称位置的字符(处理非字母数字、大小写后)。
-
指针定位:left 从字符串头部开始,right 从字符串尾部开始,相向遍历。
-
前置处理:遍历中跳过非字母数字字符(避免干扰回文判断),再将对比的字符统一转为小写。
-
判断逻辑:若出现大小写转换后不相等的字符,直接返回 false;遍历结束(left >= right)则返回 true,循环条件用 left < right(指针相遇即完成所有对比)。
JavaScript
var isPalindrome = function(s) {
let left = 0;
let right = s.length - 1;
// 无等于号:指针相遇即完成判断
while (left < right) {
// 跳过非字母数字
while (!/[a-zA-Z0-9]/.test(s[left]) && left < right) left++;
while (!/[a-zA-Z0-9]/.test(s[right]) && left < right) right--;
// 字符不相等则不是回文
if (s[left].toLowerCase() !== s[right].toLowerCase()) {
return false;
}
left++;
right--;
}
return true;
};拓展:中心扩展法(左右指针变形,适用于最长回文子串)
作为左右指针的拓展用法,中心扩展法专门解决回文子串类问题,无需单独定义通用模板,核心是利用回文串的中心对称性,用左右指针实现扩散遍历,对应题目为LeetCode 5。
LeetCode 5 最长回文子串:给你一个字符串 s,找到 s 中最长的回文子串。回文子串是指正着读和反着读都一样的子串,例如 "babad" 的最长回文子串是 "bab" 或 "aba","cbbd" 的最长回文子串是 "bb"。
解题思路:
-
核心逻辑:利用回文串的中心对称性,用左右指针从中心向两侧扩散,探索每个中心对应的最长回文子串。
-
中心分类:回文串分两种情况------奇数长度(单中心,如"aba",中心为中间字符)、偶数长度(双中心,如"bb",中心为两个相邻字符)。
-
遍历与扩散:遍历字符串每个位置,分别以当前位置为单中心、当前与下一个位置为双中心,调用中心扩展方法。
-
结果保留:每次扩散后记录当前回文子串,全程保留长度最长的回文子串,遍历结束后返回该子串。
JavaScript
// 中心扩展工具函数:传入中心左右指针,返回以该中心的最长回文子串
function expandCenter(s, l, r) {
// 扩散条件:左指针不越界 + 右指针不越界 + 左右指针指向字符相等(满足则继续扩散)
while (l >= 0 && r < s.length && s[l] === s[r]) {
l--; // 左指针左扩(向左侧延伸,探索更长回文)
r++; // 右指针右扩(向右侧延伸,探索更长回文)
}
// 退出循环时,l/r已无效(要么越界,要么字符不等),有效回文区间为 [l+1, r-1]
// slice方法左闭右开,所以end参数写r(自动取到r-1)
return s.slice(l + 1, r);
}
// 主函数:遍历所有可能的中心,找到整个字符串的最长回文子串
var longestPalindrome = function(s) {
let res = ''; // 存储最终找到的最长回文子串,初始为空
// 遍历字符串每个位置,每个位置都可能是回文中心(单中心/双中心)
for (let i = 0; i < s.length; i++) {
// 情况1:奇数长度回文(单中心),中心为当前i位置(左右指针初始都指向i)
const s1 = expandCenter(s, i, i);
// 情况2:偶数长度回文(双中心),中心为当前i和i+1位置(左右指针分别指向i和i+1)
const s2 = expandCenter(s, i, i + 1);
// 保留更长的回文子串:先对比res和s1,取更长的;再对比结果和s2,取更长的
res = res.length > s1.length ? res : s1;
res = res.length > s2.length ? res : s2;
}
// 遍历结束,返回最长回文子串
return res;
};三、倒序双指针模板(核心:避免覆盖)
模板核心场景
合并两个有序数组、有序数组的平方等,正序遍历会覆盖有效元素,需从后往前填充,对应两道高频LeetCode题目,下文将逐一附上链接并实战演练。
通用模板
JavaScript
/**
* 倒序双指针模板(避免覆盖)
* @param {Array} arr1 - 目标数组(有剩余空间)
* @param {number} len1 - arr1有效元素长度
* @param {Array} arr2 - 待合并数组
* @param {number} len2 - arr2有效元素长度
* @return {void} - 原地修改arr1
*/
function reverseTwoPointerTemplate(arr1, len1, arr2, len2) {
// 指针定义:均指向「有效元素的最后一个位置」
let p1 = len1 - 1; // arr1有效尾指针
let p2 = len2 - 1; // arr2有效尾指针
let p = len1 + len2 - 1; // 目标数组填充尾指针
// 循环条件:两个数组都有未处理元素
while (p1 >= 0 && p2 >= 0) {
// 取更大的值填充到p位置(合并有序数组)
// 取绝对值更大的值填充(有序数组平方)
if (arr1[p1] > arr2[p2]) {
arr1[p] = arr1[p1];
p1--;
} else {
arr1[p] = arr2[p2];
p2--;
}
p--; // 填充位左移
}
// 处理剩余元素(仅需处理arr2,arr1剩余元素已在原位)
while (p2 >= 0) {
arr1[p] = arr2[p2];
p--;
p2--;
}
}模板实战1:合并两个有序数组(LeetCode 88)
题目描述:给你两个按非递减顺序排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。请你合并 nums2 到 nums1 中,使合并后的数组同样按非递减顺序排列。要求:最终合并后数组不应由函数返回,而是存储在数组 nums1 中;nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0,应忽略;nums2 的长度为 n。
解题思路:
-
核心目的:避免正序合并时,nums1 的有效元素被覆盖,因此采用倒序双指针,从后往前填充。
-
指针定义:p1 指向 nums1 有效元素的最后一个位置(m-1),p2 指向 nums2 有效元素的最后一个位置(n-1),p 指向 nums1 最终填充的尾指针(m+n-1)。
-
倒序填充:循环对比 p1 和 p2 指向的元素,将较大的元素填充到 p 位置,填充后对应指针和 p 均左移。
-
剩余处理:当 nums1 遍历完(p1 < 0),若 nums2 还有剩余元素,直接将剩余元素依次填充到 nums1 剩余位置。
JavaScript
var merge = function(nums1, m, nums2, n) {
let p1 = m - 1;
let p2 = n - 1;
let p = m + n - 1;
// 倒序合并,避免覆盖nums1有效元素
while (p1 >= 0 && p2 >= 0) {
if (nums1[p1] > nums2[p2]) {
nums1[p] = nums1[p1];
p1--;
} else {
nums1[p] = nums2[p2];
p2--;
}
p--;
}
// 处理nums2剩余元素
while (p2 >= 0) {
nums1[p] = nums2[p2];
p--;
p2--;
}
};模板实战2:有序数组的平方(LeetCode 977)
题目描述:给你一个按非递减顺序排序的整数数组 nums,返回每个数字的平方组成的新数组,要求也按非递减顺序排序。例如,nums = [-4,-1,0,3,10],返回 [0,1,9,16,100];nums = [-7,-3,2,3,11],返回 [4,9,9,49,121]。
解题思路:
-
模板变形:基于倒序双指针,利用原数组非递减特性------数组两端元素的平方可能是最大值(负数平方后可能大于正数)。
-
指针定义:left 指向数组头部(负数区),right 指向数组尾部(正数区),p 指向结果数组的尾指针(倒序填充)。
-
循环条件:用 left <= right,需处理最后一个剩余元素(避免漏处理)。
-
填充逻辑:对比 left 和 right 元素的绝对值,绝对值大的元素平方后填充到 p 位置,对应指针和 p 均左移,最终返回结果数组。
JavaScript
var sortedSquares = function(nums) {
const len = nums.length;
const res = new Array(len);
let left = 0; // 左指针(负数区)
let right = len - 1; // 右指针(正数区)
let p = len - 1; // 结果填充尾指针
// 倒序填充:取绝对值更大的平方值
while (left <= right) { // 有等于号:处理最后一个元素
const lAbs = Math.abs(nums[left]);
const rAbs = Math.abs(nums[right]);
if (lAbs > rAbs) {
res[p] = lAbs * lAbs;
left++;
} else {
res[p] = rAbs * rAbs;
right--;
}
p--;
}
return res;
};拓展:三指针分区(荷兰国旗问题,LeetCode 75)
作为对撞/分区型双指针的进阶拓展,三指针本质还是「边界维护 + 一次遍历分区」的核心思想,不单独作为通用模板,理解指针边界定义和处理逻辑即可直接解题,对应题目为LeetCode 75(荷兰国旗问题)。
指针核心定义
-
p0:0区的「下一个填充位」(0区左侧全是0,右侧为未处理区域)
-
p2:2区的「上一个填充位」(2区右侧全是2,左侧为未处理区域)
-
p:遍历指针,负责检查当前元素的归属(0/1/2区),遍历未处理区域
LeetCode 75 颜色分类:给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。我们使用整数 0、1 和 2 分别表示红色、白色和蓝色。要求:必须在不使用库内置的 sort 函数的情况下解决这个问题,且使用 O(1) 额外空间完成。
解题思路:
-
核心逻辑:通过三个指针分工维护0区、2区边界,一次遍历完成数组分区,无需额外空间,高效排序。
-
循环条件:p <= p2,因为p2右侧的元素已全部是2(已处理完毕),无需再遍历。
-
元素处理规则:遇到0则与p0交换(归位0区),p0右移;遇到2则与p2交换(归位2区),p2左移(p不移动,需重新检查交换后的值);遇到1则直接遍历下一个元素(归位中间1区)。
JavaScript
var sortColors = function(nums) {
const len = nums.length;
if(len <= 1) return;
// 指针定义(通俗版):
// p0:「0区管家」,指向「下一个要放入0的位置」(p0左边全是已排好的0)
// p2:「2区管家」,指向「下一个要放入2的位置」(p2右边全是已排好的2)
// p:「检查员」,遍历数组,逐个检查当前元素该归到哪个区
let p0 = 0;
let p2 = len - 1;
let p = 0;
// 【易错点2:循环条件】p <= p2 而非 p < len
// 原因:p2右边已经是排好的2,无需遍历;若写p < len会重复处理已排好的2
// 错误示例:while(p < len) → 遍历到p2右侧的2,可能导致交换错误
while(p <= p2) {
// 情况1:检查员发现当前元素是0 → 归到0区
if(nums[p] === 0) {
// 交换「检查员位置」和「0区下一个空位」的元素,把0归位
[nums[p0], nums[p]] = [nums[p], nums[p0]];
p0++; // 0区管家右移,准备接收下一个0
// 【易错点3:p的重置】p = Math.max(p, p0) 避免p回退到已处理的0区
// 原因:p0左边全是0,p若小于p0,会重复检查已排好的0,导致逻辑混乱
// 错误示例:漏掉这行 → p可能回退到p0左侧,重复交换0,最终数组出错
p = Math.max(p, p0);
}
// 情况2:检查员发现当前元素是2 → 归到2区
else if(nums[p] === 2) {
// 交换「检查员位置」和「2区下一个空位」的元素,把2归位
[nums[p2], nums[p]] = [nums[p], nums[p2]];
p2--; // 2区管家左移,准备接收下一个2
// 【易错点4:交换2后p不移动】
// 原因:交换过来的元素可能是0/1,需要重新检查当前位置的新元素
// 错误示例:交换2后写p++ → 跳过新交换来的0/1,导致漏处理(比如[2,0,1]会排序失败)
}
// 情况3:检查员发现当前元素是1 → 1本就该在中间,无需处理,直接检查下一个
else if(nums[p] === 1) {
p++;
}
}
};四、避坑清单(模板核心细节)
| 模板/拓展类型 | 关键细节 | 易错点 |
|---|---|---|
| 快慢指针 | 1. slow定位(最后一个/下一个) 2. 长度计算(+1/直接返回) | 混淆slow定位导致长度错误 |
| 左右指针 | 1. while条件是否加等于号 2. 中心扩展越界判断 | 漏写越界条件、错用等于号 |
| 倒序双指针 | 1. 从后往前填充 2. 处理剩余元素(仅处理次要数组) | 正序填充覆盖有效元素 |
| 三指针分区(拓展) | 1. p ≤ p2(而非 p < len) 2. 交换 2 后 p 不移动 | 循环条件写错、交换 2 后 p++ 导致漏处理 |
五、模板使用步骤
- 定题型:快慢(去重/移除)、左右(对撞/回文)、倒序(合并/平方)、三指针(分区)。
- 定指针:写清每个指针的语义(如 slow = 已保留最后一项 / 下一个填充位;p0/p2 = 0 区/2 区下一个填充位)。
- 套模板:按对应小节写循环条件与移动逻辑,拓展题按「边界 + 一次遍历」微调。
- 查细节:等于号(< 还是 ≤)、新长度(slow+1 还是 slow)、剩余元素是否只处理一方。