体系
理论
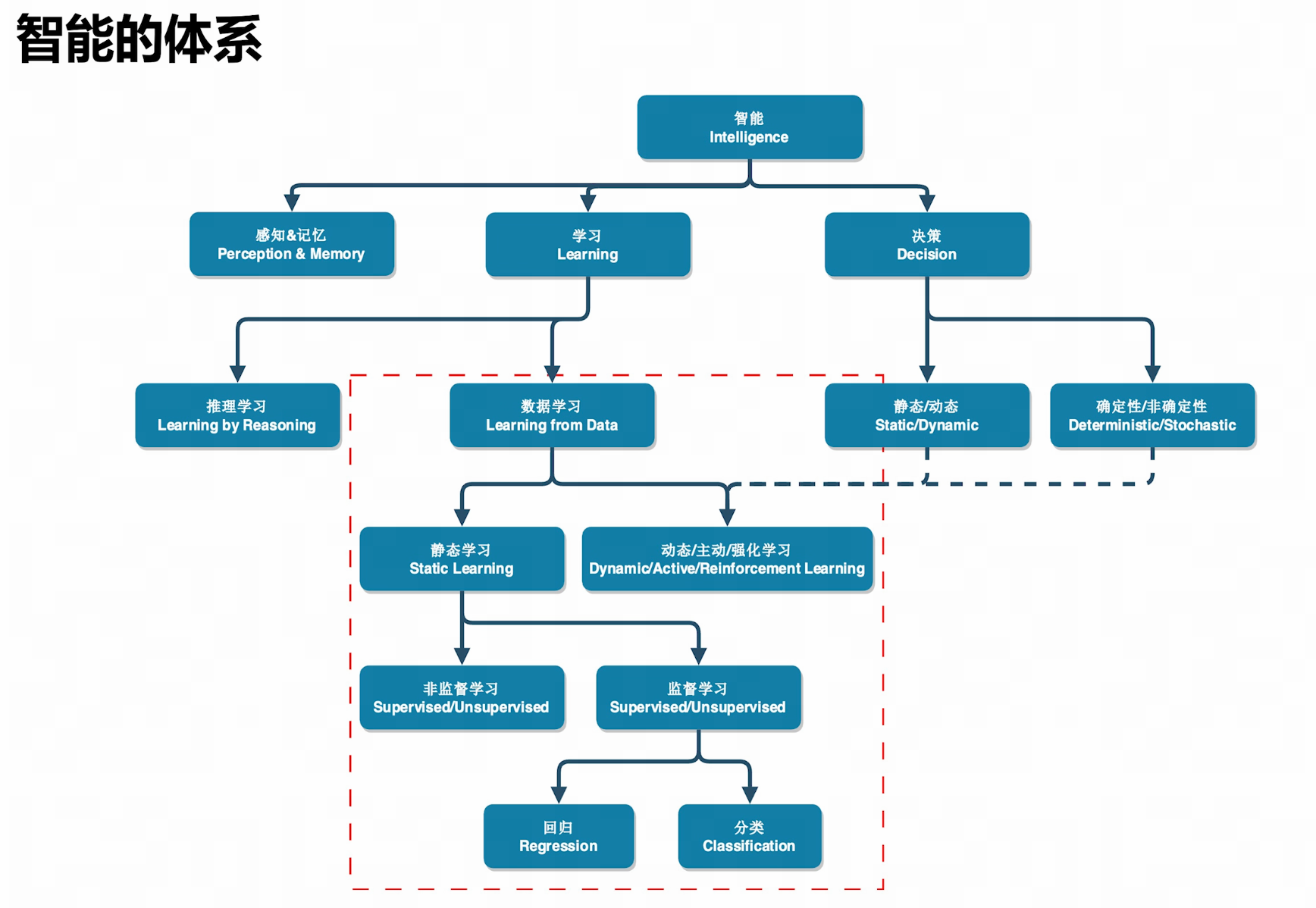
感知&记忆
获取数据、存储数据
学习
推理学习:自下而上,如数学。公理,证明,推论
数据学习:自上而下,如物理(可能有颠覆风险)。数据观测->理论解释->实验验证
决策
决策问题先给出抽象框架,
- 决策变量
- 目标函数与优化方向:目标与决策之间的关系
- 约束:限制决策的范围
然后建模,将问题量化描述,再交给机器求解
开发
机器学习算法的任务是,基于给定的数据集和结构,求解一个优化问题以找到最佳的参数B0和B1,从而实现拟合度最大化。
工程部署
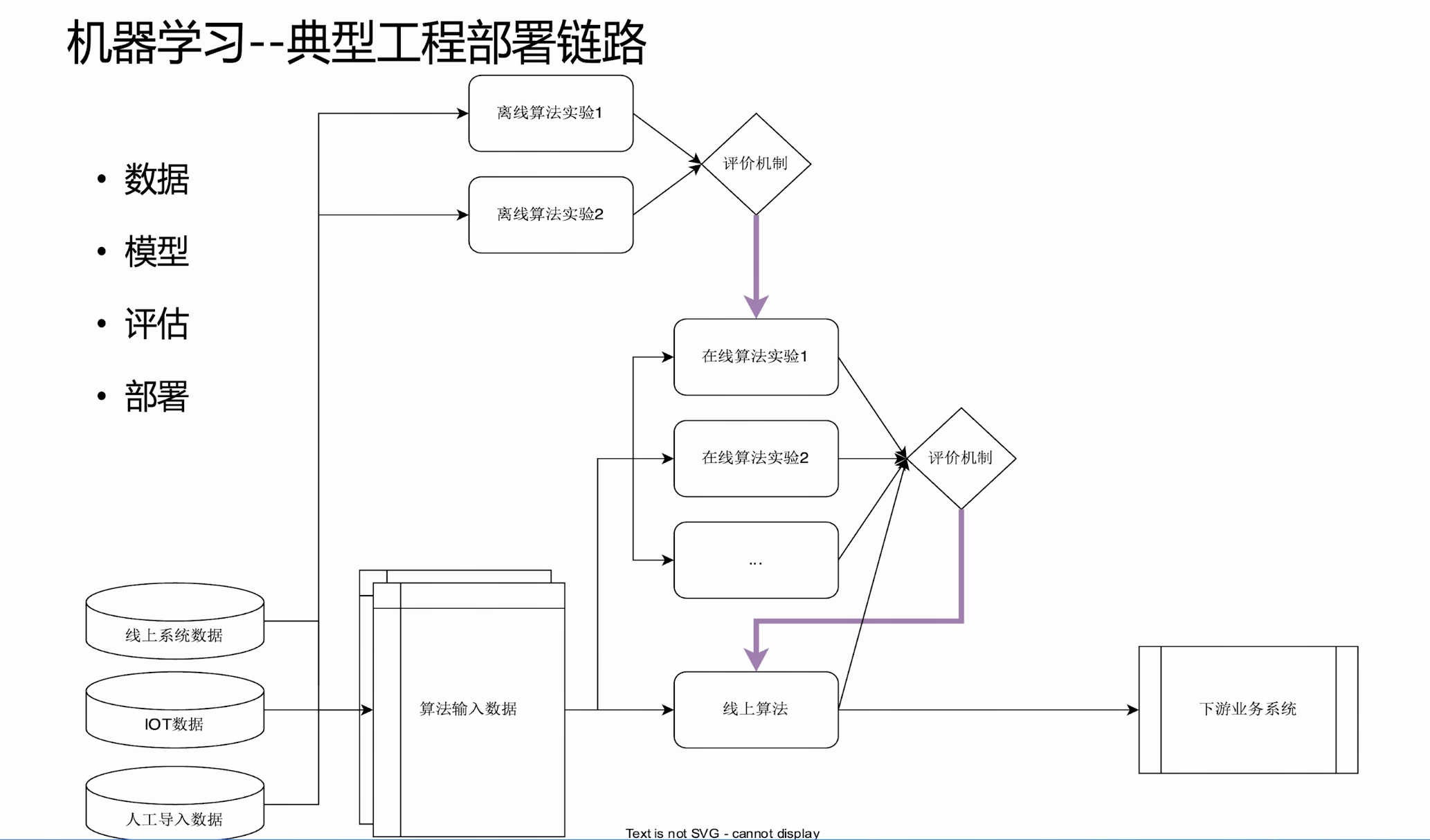
数据-模型-评估-部署
算法开发链路
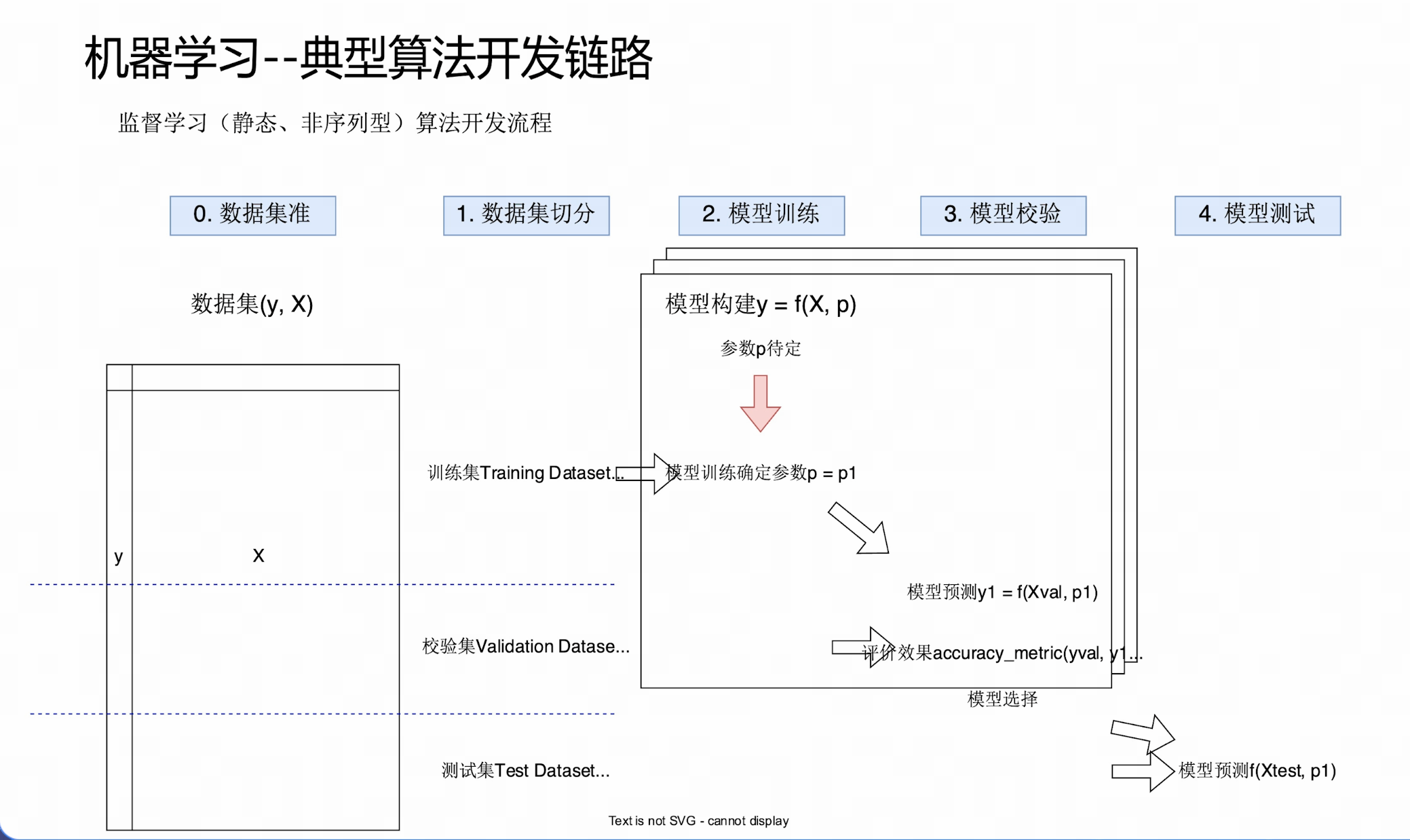
数据集准备-数据集切分-模型训练-模型校验-模型测试
算法演进
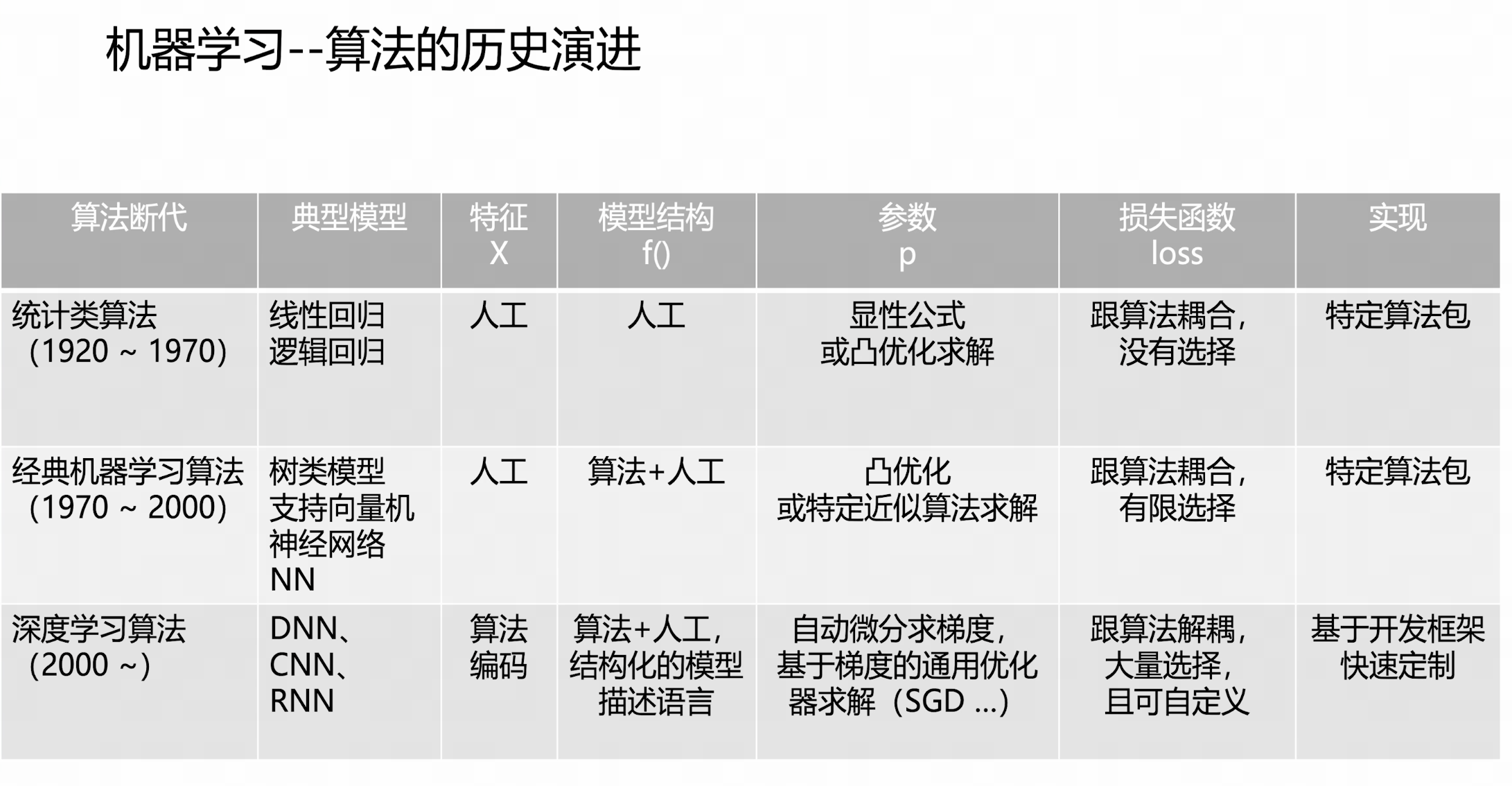
底层逻辑
- 算法工程师:把复杂的f()结构化,参数化;利用人类的先验知识,尽量缩小搜索空间
- 算法:利用算力,在给定模型结构的框架下,在数据y~x的监督下,找到最优参数实现拟合
- 尽量让算法来做
挑战
- 可预测性:信号vs噪声
- 欠拟合:模型未能捕捉数据基本规律 ,表现为训练误差和测试误差均高(模型过于简单,无法学习数据复杂度)
- 过拟合:模型过度记忆训练数据噪声/特定样本 ,表现为训练误差低但测试误差高(模型复杂度过高,失去泛化性)
- 时间稳定性:机器尝试学习的真实关系y~x是不是随时间变化的
- 个性vs共性:比如预测癌症的模型,是否根据性别、年龄区分不同数据集
3种过拟合情况
本质:模型"死记硬背"训练数据中的噪声和特定模式,丧失对底层数据分布的泛化能力。
算法人员在以下开发步骤中的操作易"好心做坏事",导致过拟合
数据
原因:特征维度高
模型训练
原因:使用高阶多项式等,模型结构复杂
解法:模型内部有复杂性、波动性控制机制
模型校验
原因:模型数量多,有限校验集评估模型出现随机性,如基金经理排行榜
解法:增加校验集数据量;更高效地利用有限数据集(k重交叉验证)
统计类方法

主要思想
统计类方法核心为"从数据中推断总体规律",其哲学基础来自经典统计学
工作模式
统计类方法的工作流程强调严谨性、可重复性和可解释性,主要包括以下三个关键环节:
1. 特征工程
目标:使数据符合模型假设,提升模型稳定性和解释力。
| 操作 | 目的 | 常用方法 |
|---|---|---|
| 变量变换 | 满足线性、正态性假设 | 对数变换(log)、平方根、Box-Cox变换 |
| 处理异常值 | 减少极端值对参数估计的影响 | 使用IQR法则、Z-score检测并处理 |
| 离散化/分箱 | 捕捉非线性趋势 | 等频分箱、基于树的分箱(如决策树桩) |
| 构造交互项 | 显式建模特征间协同效应 | x 1×x 2 、多项式项 x2 |
| 标准化/归一化 | 保证系数可比性 | Z-score标准化(均值为0,方差为1) |
2. 变量选择
目标:在众多候选变量中筛选出真正对响应变量有解释力的变量,防止过拟合。
常见策略:
| 方法 | 原理 | 优点 | 缺点 |
|---|---|---|---|
| 逐步回归 (Stepwise) | 通过AIC/BIC逐步添加/删除变量 | 自动化,易于实现 | 易陷入局部最优,可能过拟合 |
| Lasso回归 (L1正则化) | 惩罚绝对系数和,强制部分系数为0 | 自动变量选择,适合高维数据 | 在强相关变量中随机选其一 |
| 岭回归 (L2正则化) | 惩罚系数平方和,压缩但不归零 | 处理多重共线性效果好 | 不进行变量筛选 |
| 弹性网 (Elastic Net) | L1 + L2 混合惩罚 | 兼顾Lasso和Ridge优点 | 超参数需调优 |
| 基于p值的筛选 | 保留p < 0.05的显著变量 | 统计意义明确 | 多重比较问题,易误判 |
推荐做法:结合领域知识 + 正则化方法 + 交叉验证,避免纯依赖p值。
3. 多模型结构比对
目标:在多个候选模型中选择最优结构,平衡拟合优度与复杂度。
常用比较方法:
| 方法 | 适用场景 | 特点 |
|---|---|---|
| AIC(Akaike Information Criterion) | 非嵌套模型比较 | 偏向稍复杂但预测能力强的模型 |
| BIC(Bayesian Information Criterion) | 大样本下更优 | 惩罚更重,倾向于简单模型 |
| 似然比检验(LRT) | 嵌套模型比较(如全模型 vs 子集) | 统计显著性检验,p值驱动 |
| 交叉验证(CV)误差 | 所有模型通用 | 最接近真实泛化误差,推荐使用 |
| 残差分析 | 模型诊断 | QQ图看正态性,残差图看异方差、非线性 |
评估口径
- 单点评价口径:针对单个样本或预测点的误差/正确性定义
- 汇总方式:将多个单点结果聚合为整体指标的方法
回归任务
目标:预测连续值(如房价、温度、销售额)
- 单点评价口径(误差度量)
| 指标 | 定义 | 公式 | 特点 |
|---|---|---|---|
| 绝对误差(AE) | 预测值与真实值之差的绝对值 | ||
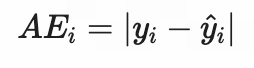 |
直观,单位与目标一致 | ||
| 平方误差(SE) | 差值的平方 | ||
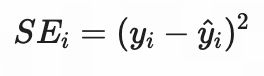 |
放大大误差,利于优化(可导) | ||
| 相对误差(RE) | 以真实值为基准的误差比例 | ||
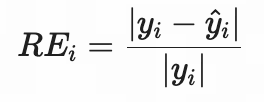 |
适用于量纲差异大的数据 |
说明:这些是"单样本"层面的误差,后续需通过"汇总方式"得到全局指标。
- 汇总方式(聚合策略)
| 汇总方式 | 对应全局指标 | 公式 | 优点 | 缺点 |
|---|---|---|---|---|
| 均值(Mean) | MAE(Mean Absolute Error) | |||
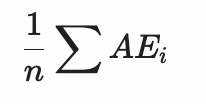 |
稳健,不易受异常值影响 | 不强调大错误 | ||
| 均方(Mean Square) | MSE(Mean Squared Error) | |||
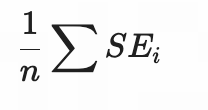 |
数学性质好,广泛用于损失函数 | 对异常值敏感 | ||
| 分位数(Quantile) | MAPE(Mean Absolute Percentage Error) | |||
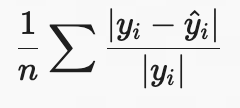 |
无量纲,便于跨任务比较 | 当 y__i≈0 时不稳定 |
二分类
目标:预测样本属于正类(1)或负类(0)
- 单点评价口径(预测正确性)
每个样本的预测结果可归为四类(混淆矩阵基础):
| 类型 | 条件 | 含义 |
|---|---|---|
| TP(True Positive) | 真实=1,预测=1 | 正确发现正类 |
| FP(False Positive) | 真实=0,预测=1 | 误报(错判为正) |
| FN(False Negative) | 真实=1,预测=0 | 漏报(漏掉正类) |
| TN(True Negative) | 真实=0,预测=0 | 正确识别负类 |
- 汇总方式(基于混淆矩阵的比率计算)
| 汇总逻辑 | 指标 | 公式 | 关注点 |
|---|---|---|---|
| 预测为正的可信度 | 精度(Precision) | TP/TP +FP | 少误报(FP) |
| 真实为正的覆盖率 | 召回率(Recall) (又称查全率、灵敏度) | TP/TP +FN | 少漏报(FN) |
| 整体正确比例 | 准确率(Accuracy) | TP +TN/n | 简单直观,但类别不平衡时失效 |
| 排序能力 | AUC-ROC | ROC曲线下面积 | 不依赖阈值,衡量模型整体判别能力 |
优势与劣势
优点:
- 模型结构可读、结果可解释
- 部署简单(两个向量乘一下)
缺点:
- f()的线性结构约束
- 特征工程负担重,需人工提取
- 过拟合风险随数据规模上升而加剧
使用场景
推荐使用场景:
- 需要向管理层、监管机构解释模型逻辑
- 数据量较小,但需严谨推断
- 关注变量重要性与因果关系
- 实时性要求高,资源有限
- 需输出置信区间或风险范围
不推荐场景:
- 数据高度非线性(如图像识别)
- 特征极多且自动组合复杂(如推荐系统)
- 仅追求预测精度,不关心"为什么"
经典机器学习方法
主要思想
**重模型:**灵活且强大的模型结构f(),近似求解参数p
- 引入非线性结构,把复杂结构参数化,用算法来解(数据驱动)
- validation防止过拟合
**重特征:**通过加工特征X,融入人对问题的理解(先验知识)
线性模型拓展:Lasso
(Least Absolute Shrinkage and Selection Operator)
最小绝对收缩与选择算子
其基本原理是在普通最小二乘法的基础上,引入L1正则化项,通过最小化目标函数来实现模型的特征选择和系数稀疏化。
原理
- 普通线性回归(OLS)
目标:最小化预测误差
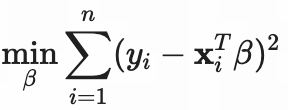
问题:不限制系数大小,容易过拟合,尤其当 p ≫n 时。(p为特征β
数量)
- Lasso 回归(带 L1 正则化)
目标:
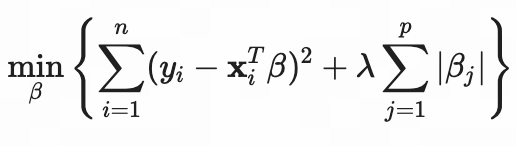
其中:
- 第一项:残差平方和(RSS),衡量拟合优度
- 第二项:L1 正则化项,所有系数绝对值之和
- λ ≥0 :正则化参数,控制惩罚强度
λ =0 :退化为 OLS
λ →∞ :所有系数被压为 0
最优 λ :通过交叉验证选择