进阶篇-机器学习篇-2--机器学习数学基础：不用啃课本，够用就行

机器学习数学基础：不用啃课本，够用就行

作者：Weisian

发布时间：2026年2月12日

别被"数学恐惧症"吓退------机器学习需要的数学，远没有你想象中那么高深。

很多人一听说"学机器学习要懂数学"，立刻想到微积分、线性代数、概率论三大厚本教材，瞬间打退堂鼓。

但真相是：你不需要成为数学家，只需要掌握"刚好够用"的核心概念。

这篇文章为你精炼出真正会在模型中用到的数学工具，每一块都明确告诉你：

它是什么？
为什么重要？
它服务于哪个具体模型？

拒绝无效内卷，只学能落地的部分。

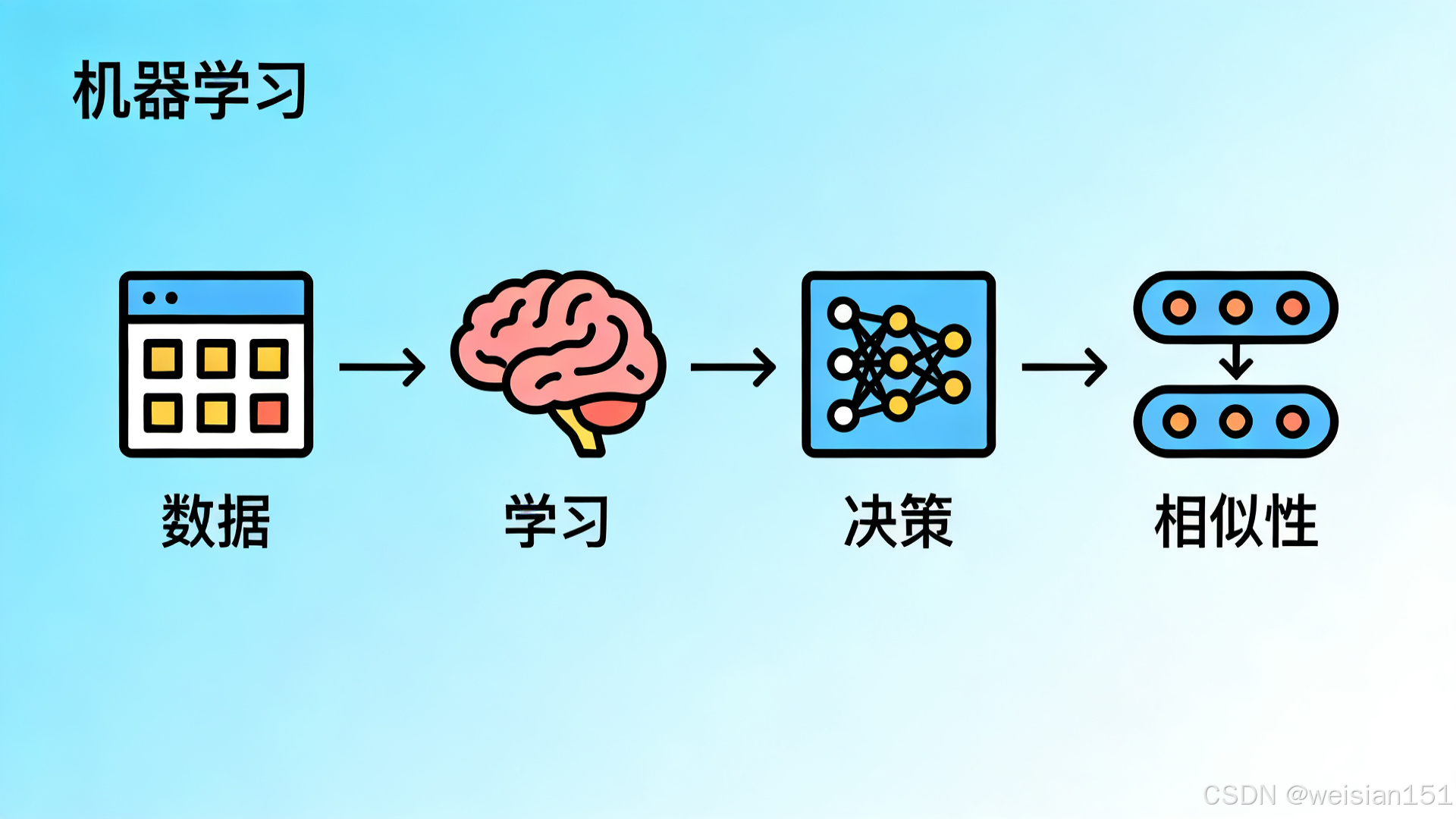
一、先讲清楚：为什么机器学习需要数学？

你不用成为数学家，但必须知道：

数据怎么表示 → 向量、矩阵
模型怎么"学习" → 导数、梯度
怎么判断"像不像" → 距离、相似度
怎么从不确定中做决策 → 概率、统计

每一个数学知识点，都对应一个真实算法。

我会在每一节都告诉你：这个数学，是给哪个模型用的。

二、向量与矩阵：机器学习的数据"容器"

如果你打开任何一个数据集，第一眼看到的一定是表格：

行 = 样本（一条用户记录、一张图片、一笔交易）
列 = 特征（年龄、消费金额、像素值）

这就是机器学习的语言------向量和矩阵。

1. 向量：一条数据

定义：一个有序的数字列表，代表一个样本的所有特征。

python 复制代码

用户A = [年龄25, 年收入15万, 最近30天登录12次]

👉 数学表示 ：x = [25, 15, 12]

在哪用：

KNN、SVM、聚类：计算两个样本"像不像"，本质就是算两个向量的距离
神经网络：每一层的输入、输出都是向量

2. 矩阵：整个数据集

定义：多个向量堆叠成的二维表格。

复制代码

     [年龄 收入 登录次数]
用户A [ 25   15     12  ]
用户B [ 34   22      5  ]
用户C [ 19    8     20  ]

👉 数学表示 ：X ∈ ℝ³ˣ³（3行3列的实数矩阵）

在哪用：

线性回归 ：y = X·w，整个数据集的预测一次性算完
PCA降维：对协方差矩阵做特征分解
深度学习：批量数据就是矩阵运算

✅ 一句话记住 ：向量是一条样本，矩阵是一堆样本------机器学习吃的"饭"就是这个形状。

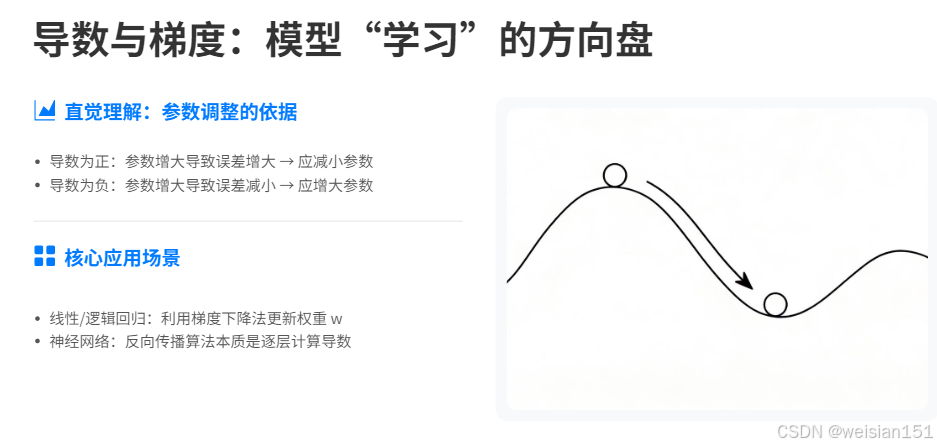
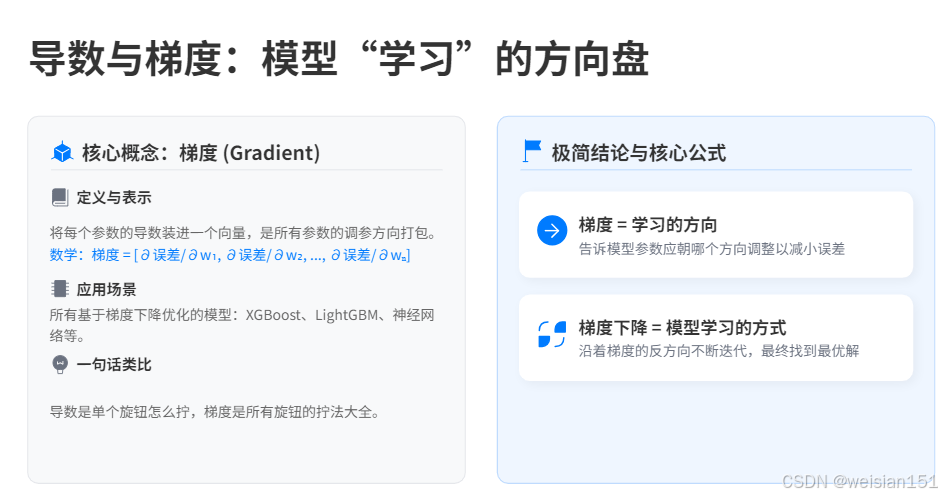
三、导数与梯度：模型"学习"的方向盘

模型怎么从"猜得很烂"变成"猜得很准"？
靠的是不断调整参数，让错误变小。

问题是：往哪个方向调？

1. 导数：一个参数的调参方向

直觉理解 ：导数告诉你------如果把某个参数增加一点点 ，误差会变大还是变小。

导数为正 → 参数增大，误差增大 → 应该减小参数
导数为负 → 参数增大，误差减小 → 应该增大参数

👉 这不就是调参的依据吗？

在哪用：

线性回归：梯度下降法更新权重 w
逻辑回归：同样是梯度下降
神经网络：反向传播就是在逐层计算导数

2. 梯度：所有参数的调参方向打包

定义：把每个参数的导数装进一个向量。

复制代码

梯度 = [∂误差/∂w₁, ∂误差/∂w₂, ..., ∂误差/∂wₙ]

在哪用：

任何用梯度下降优化的模型：XGBoost、LightGBM、神经网络......
一句话 ：没有梯度，模型永远不知道往哪儿走。

✅ 一句话记住 ：导数是单个旋钮怎么拧，梯度是所有旋钮的拧法大全。
✅ 极简结论 ：
梯度 = 学习的方向
梯度下降 = 模型学习的方式

四、概率与统计：让模型"不确定地"决策

现实世界充满不确定性：

这条交易有**80%**可能是盗刷
这张图片有**90%**的概率是猫
这个用户很可能会流失

机器学习必须学会------不仅给出答案，还要给出"有多确定"。

1. 概率（Probability）：不确定性的度量

一句话：某件事发生的可能性大小。

例子：垃圾邮件识别

P(垃圾邮件 | 包含"中奖") = 0.95

在哪用：

朴素贝叶斯 ：核心就是
P(类别∣特征)∝P(特征∣类别)⋅P(类别) P(\text{类别}|\text{特征}) \propto P(\text{特征}|\text{类别}) \cdot P(\text{类别}) P(类别∣特征)∝P(特征∣类别)⋅P(类别)
逻辑回归：输出不是0/1，而是"属于正类的概率"
推荐系统：CTR预估（点击率）本质是概率预测

2. 期望（Expectation）：平均意义上的预测

一句话：加权平均。

在哪用：

评估指标：MSE（均方误差）本质是误差平方的期望
强化学习：价值函数就是累积奖励的期望

3. 方差（Variance）：预测的稳定性

一句话：数据稳不稳定，波不波动。

方差小 → 数据集中、稳定
方差大 → 数据分散、波动大

在机器学习里：

方差太大 → 过拟合，模型太飘
方差太小 → 欠拟合，太呆板

在哪用：

模型诊断：高方差 = 过拟合（记得太死，换题就懵）
集成学习：随机森林降低预测方差，Bagging的核心原理

4. 极大似然估计（MLE）：模型怎么从数据反推规律？

✅ 首先你要知道：

似然（Likelihood）：在给定参数下，观测到当前数据的"可能性"。
极大似然估计：找到一组参数，使得当前数据出现的可能性最大。

🎯 为什么重要？

这是监督学习中最常用的参数学习思想------不是随便猜参数，而是找"最能解释已有数据"的那一组。

例子：

扔硬币10次，9次正面 → 最可能的概率是 0.9。

机器学习训练 ：
给定数据 → 找最优参数 → 极大似然。

在哪用：

逻辑回归：损失函数就是从极大似然推导出来的
线性回归：最小二乘法在误差服从正态分布的假设下等价于极大似然估计
几乎所有概率模型的训练：都是在最大化似然函数

💡 例如：逻辑回归的损失函数（交叉熵）本质上就是负对数似然，最小化损失 = 最大化似然。

五、距离与相似度：判断"像不像"

机器学习大量工作可以归结为：找相似的，区分不相似的。

怎么量化"相似"？距离。

1. 欧氏距离（Euclidean Distance）

定义：二维空间的两点距离 √[(x₁−x₂)² + (y₁−y₂)²]，推广到n维就是各维度差平方和再开方。

一句话 ：衡量空间中两点的"直线距离"。 越近 → 越相似。

公式：
d(x,y)=∑i=1n(xi−yi)2 d(\mathbf{x}, \mathbf{y}) = \sqrt{\sum_{i=1}^n (x_i - y_i)^2} d(x,y)=i=1∑n(xi−yi)2

在哪用：

KNN：找最近的K个邻居
K-Means：把点分给离它最近的中心点
线性回归 ：最小二乘法本质是最小化预测值与真实值的欧氏距离

是的，你第一次见到的那个 y = ax + b，背后已经是距离度量在发挥作用了。

2. 余弦相似度（Cosine Similarity）

一句话：衡量两个向量的"方向是否一致"，忽略大小，夹角越小越相似。

方向一样 → 相似度 = 1
方向垂直 → 相似度 = 0
方向相反 → 相似度 = -1

公式：
cos(θ)=x⋅y∥x∥∥y∥ \text{cos}(\theta) = \frac{\mathbf{x} \cdot \mathbf{y}}{\|\mathbf{x}\| \|\mathbf{y}\|} cos(θ)=∥x∥∥y∥x⋅y

在哪用：

文本匹配：TF-IDF向量间的相似度
推荐系统：找"品味相似"的用户
图像检索：特征向量方向越一致，内容越相关

✅ 一句话区分 ：欧氏距离看绝对差异，余弦相似度看相对比例。

💡 小技巧 ：数值型特征用欧氏距离，文本/高维稀疏特征用余弦相似度。

六、一个扎心的事实：你不需要等数学"学完"

很多人学机器学习的误区是：先把数学啃透，再碰代码。

结果呢？

微积分上册还没翻完，热情已经凉了
公式推导了三页纸，也不知道这东西到底干嘛用
越学越觉得自己"不配写代码"

正确的姿势恰恰相反：

先跑通第一个模型（哪怕只是调包）
看到"损失函数""梯度"这些词，产生好奇
带着问题回头看数学------原来导数就是干这个的！

✅ 数学不是门槛，而是梯子。

你不需要爬完所有台阶再出发，只需要在够不着的时候，伸手搭上一级。

七、今天就能做的三件小事

1. 打开 Jupyter，敲三行代码

python 复制代码

import numpy as np

# 向量：一个用户的特征
user = np.array([25, 150000, 12])

# 矩阵：三个用户的数据集
users = np.array([[25, 150000, 12],
                  [34, 220000, 5],
                  [19, 80000, 20]])

print(users.shape)  # (3, 3)

你已经在用矩阵了，只是没意识到。

2. 算一次欧氏距离

python 复制代码

from scipy.spatial.distance import euclidean

a = [25, 150000, 12]
b = [34, 220000, 5]

dist = euclidean(a, b)
print(f"用户A和B的距离: {dist:.2f}")

这就是KNN找邻居的底层操作。

3. 观察一次梯度下降的效果（可视化）

python 复制代码

import matplotlib.pyplot as plt
import numpy as np

# 模拟梯度下降：寻找函数最小值
x = np.linspace(-10, 10, 100)
y = x**2 + 2*x + 1  # 一个简单的二次函数

# 梯度下降过程
current_x = 8
lr = 0.1
xs = [current_x]

for _ in range(20):
    gradient = 2*current_x + 2  # 导数
    current_x = current_x - lr * gradient
    xs.append(current_x)

plt.plot(x, y)
plt.scatter(xs, [x_i**2 + 2*x_i + 1 for x_i in xs], color='red')
plt.title("梯度下降：红点逐渐走向最低点")
plt.show()

你看，梯度下降不是天书，是肉眼可见的"下山"。

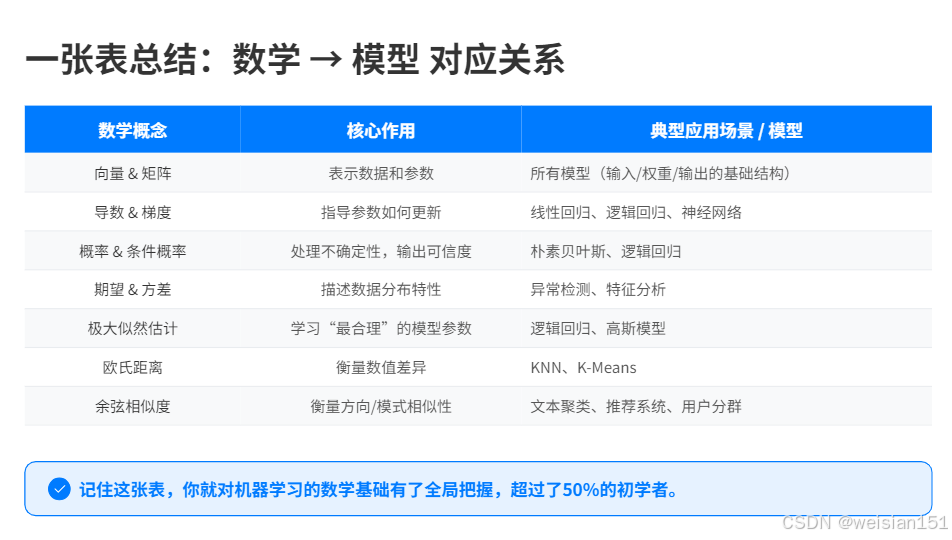
八、一张表总结：数学 → 模型对应关系

数学概念	核心作用	典型应用场景 / 模型
向量 & 矩阵	表示数据和参数	所有模型（输入/权重/输出的基础结构）
导数 & 梯度	指导参数如何更新	线性回归、逻辑回归、神经网络
概率 & 条件概率	处理不确定性，输出可信度	朴素贝叶斯、逻辑回归
期望 & 方差	描述数据分布特性	异常检测、特征分析
极大似然估计	学习"最合理"的模型参数	逻辑回归、高斯模型
欧氏距离	衡量数值差异	KNN、K-Means
余弦相似度	衡量方向/模式相似性	文本聚类、推荐系统、用户分群

✅ 记住这张表，你就超过了50%的初学者。

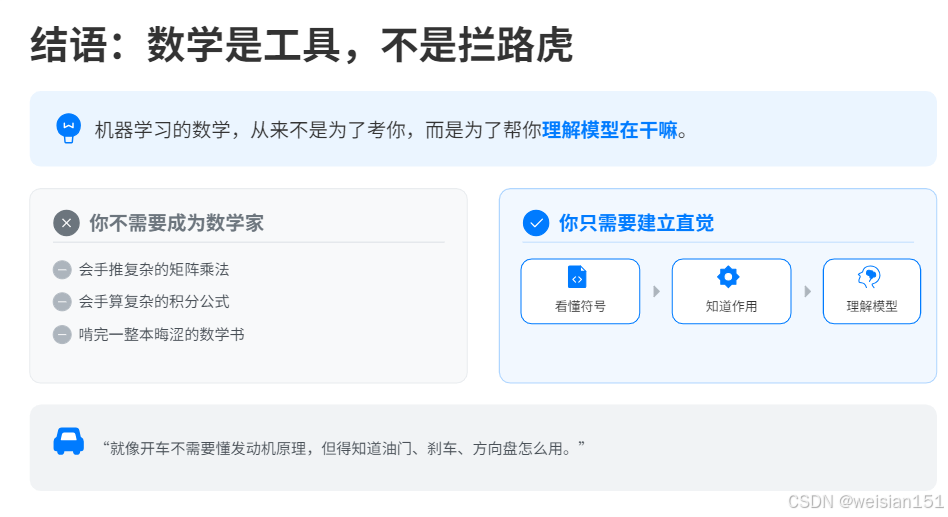
结语：数学是工具，不是拦路虎

机器学习的数学，从来不是为了考你，而是为了帮你理解模型在干嘛。

你不需要：

会手推矩阵乘法
会手算复杂积分
啃完一整本数学书

你只需要：

看懂符号 → 知道作用 → 能理解模型
向量矩阵 → 装数据
梯度 → 让模型学习
概率 → 让模型判断
距离 → 让模型识别相似

就像开车不需要懂发动机原理，但得知道油门、刹车、方向盘怎么用。

思考题（互动打卡）

试着回忆你用过的某个APP功能（比如音乐推荐、人脸美颜、快递预计送达时间），猜一猜它背后可能用到了上述哪种数学工具？

哪怕只是模糊的联想，也欢迎在评论区写下你的想法------把数学和现实连接起来，你就已经走在了正确的路上。

进阶篇-机器学习篇-2--机器学习数学基础：不用啃课本，够用就行

机器学习数学基础：不用啃课本，够用就行

一、先讲清楚：为什么机器学习需要数学？

二、向量与矩阵：机器学习的数据"容器"

1. 向量：一条数据

2. 矩阵：整个数据集

三、导数与梯度：模型"学习"的方向盘

1. 导数：一个参数的调参方向

2. 梯度：所有参数的调参方向打包

四、概率与统计：让模型"不确定地"决策

1. 概率（Probability）：不确定性的度量

2. 期望（Expectation）：平均意义上的预测

3. 方差（Variance）：预测的稳定性

4. 极大似然估计（MLE）：模型怎么从数据反推规律？

✅ 首先你要知道：

🎯 为什么重要？

五、距离与相似度：判断"像不像"

1. 欧氏距离（Euclidean Distance）

2. 余弦相似度（Cosine Similarity）

六、一个扎心的事实：你不需要等数学"学完"

七、今天就能做的三件小事

1. 打开 Jupyter，敲三行代码

2. 算一次欧氏距离

3. 观察一次梯度下降的效果（可视化）

八、一张表总结：数学 → 模型 对应关系

结语：数学是工具，不是拦路虎

八、一张表总结：数学 → 模型对应关系