
异常检测定义
根据输入的数据,对不符合预期模式的数据进行识别。
概率密度:
概率密度是描述随机变量在某个确定点附近可能性的函数。(听起来有点绕)
拓展下概率密度函数求概率
f(x)是概率密度函数,x落在a到b区间的概率就是,对于f(x)在区间[a,b]求积分。
现在的问题是单说一个f(a)或f(b)这个概率密度值有什么含义。单点的概率密度总结起来三句话
1、不是概率
2、是密集程度的一种表示
3、这个单点的概率密度值越大,越说明X(样本)越喜欢在这个单点值附件扎堆儿。
口诀:
概率密度看高低,判断哪里更密集。
真正概率看面积,单点永远都是0。
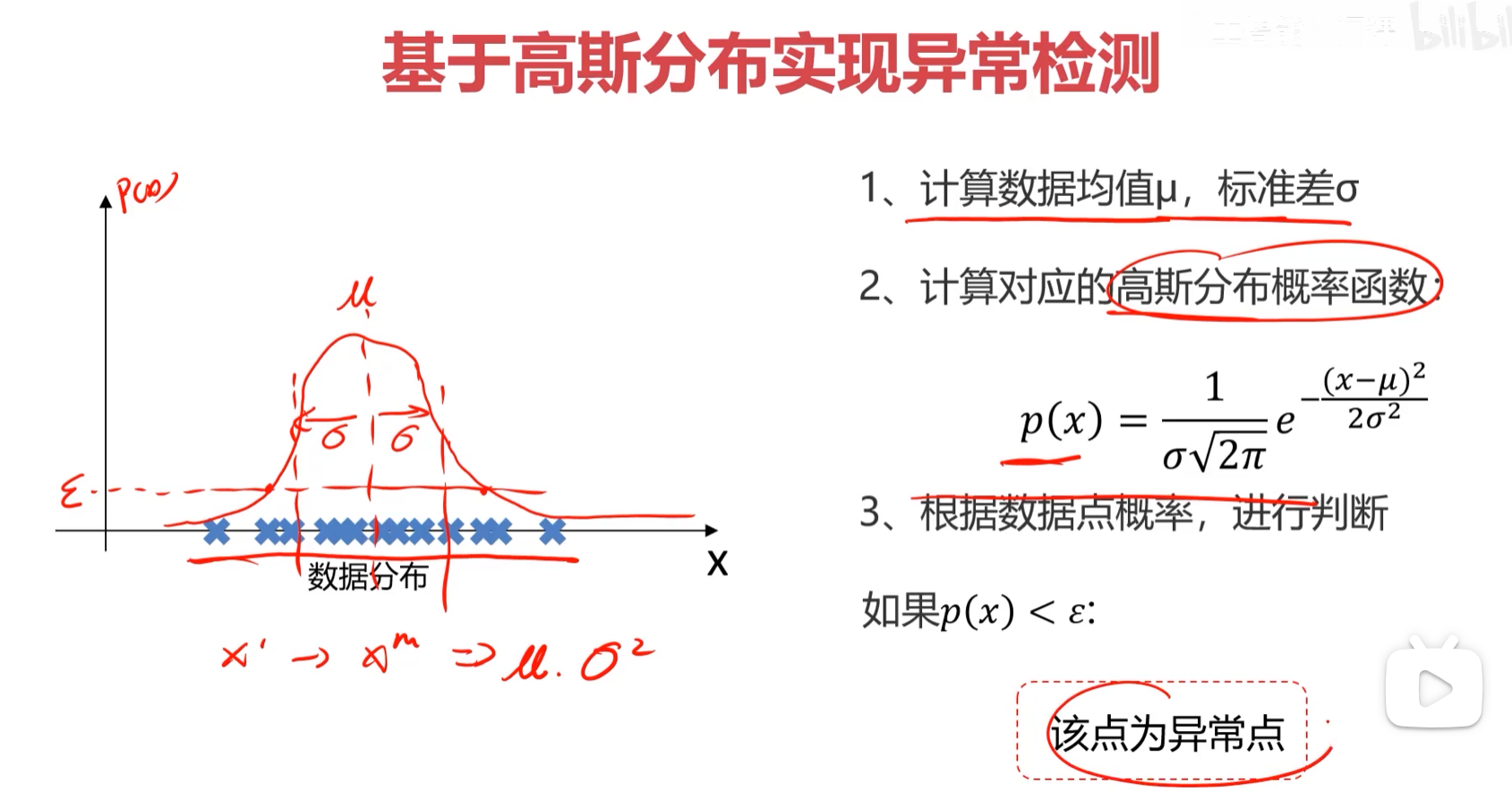
基于概率分布如何做异常检测
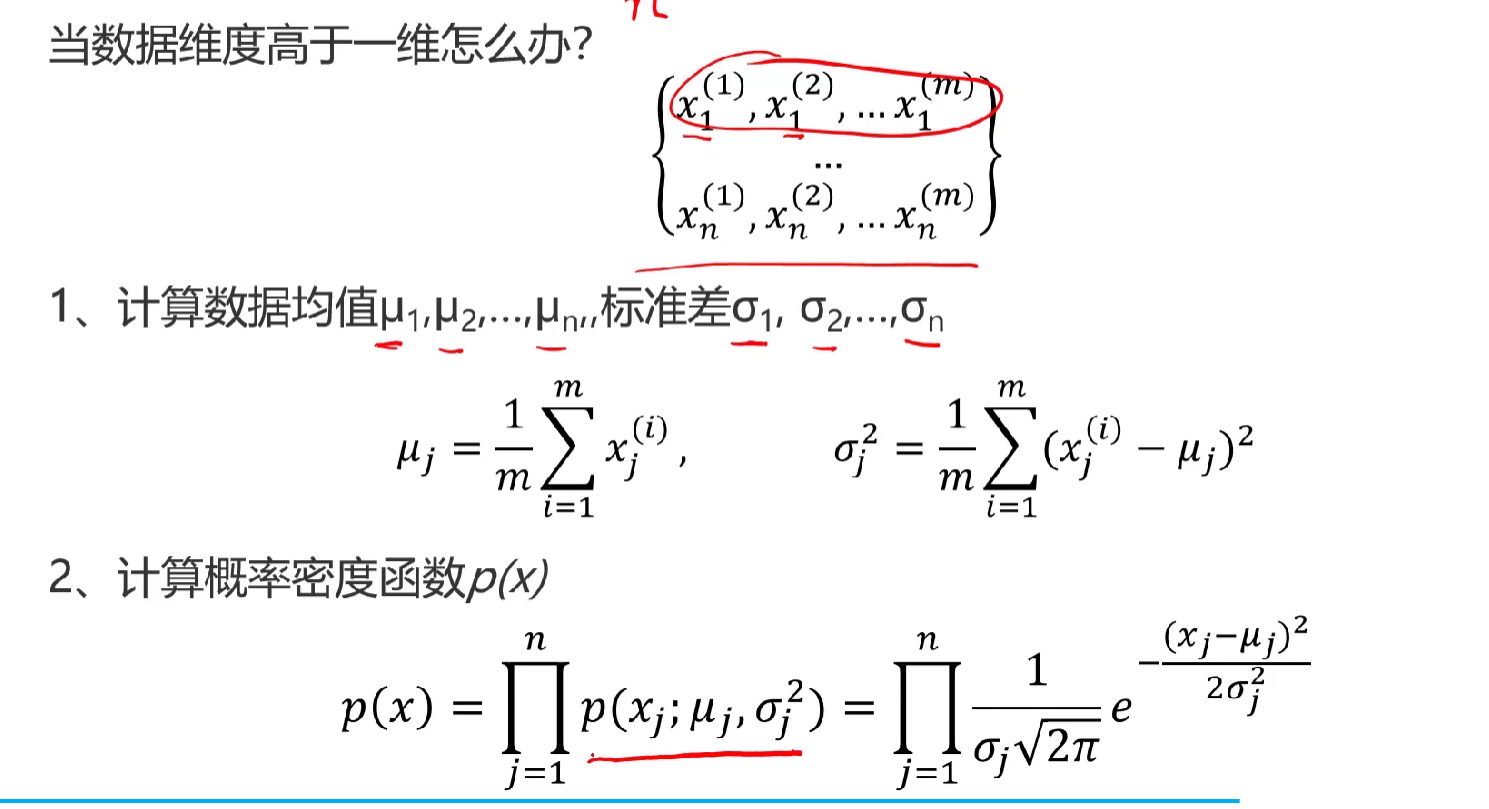
主成分分析(PCA)
数据降维
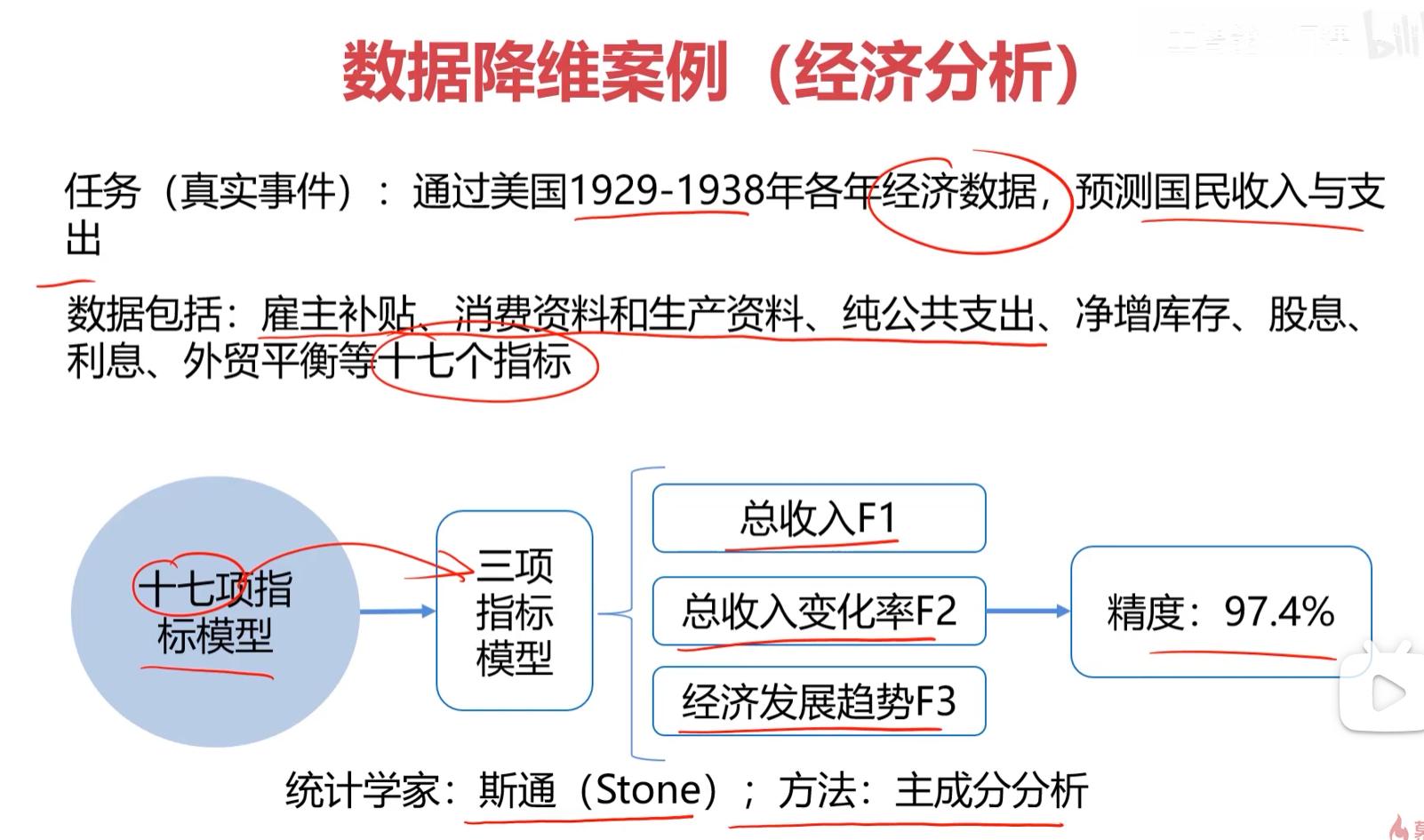
数据降维是指,在某些限定条件下,降低随机变量的个数,得到一组不相关的"主变量"过程。
比如举的这个例子17个指标最后降维成3个
作用:
1、减少模型数据分析量,提高分析效率,降低计算难度
2、实现数据可视化(二维,三维)
目标:寻找一个K维(K<N)的数据,使他们反应数据的具体特征
核心:在信息损失尽可能小的情况下,降低数据维度。
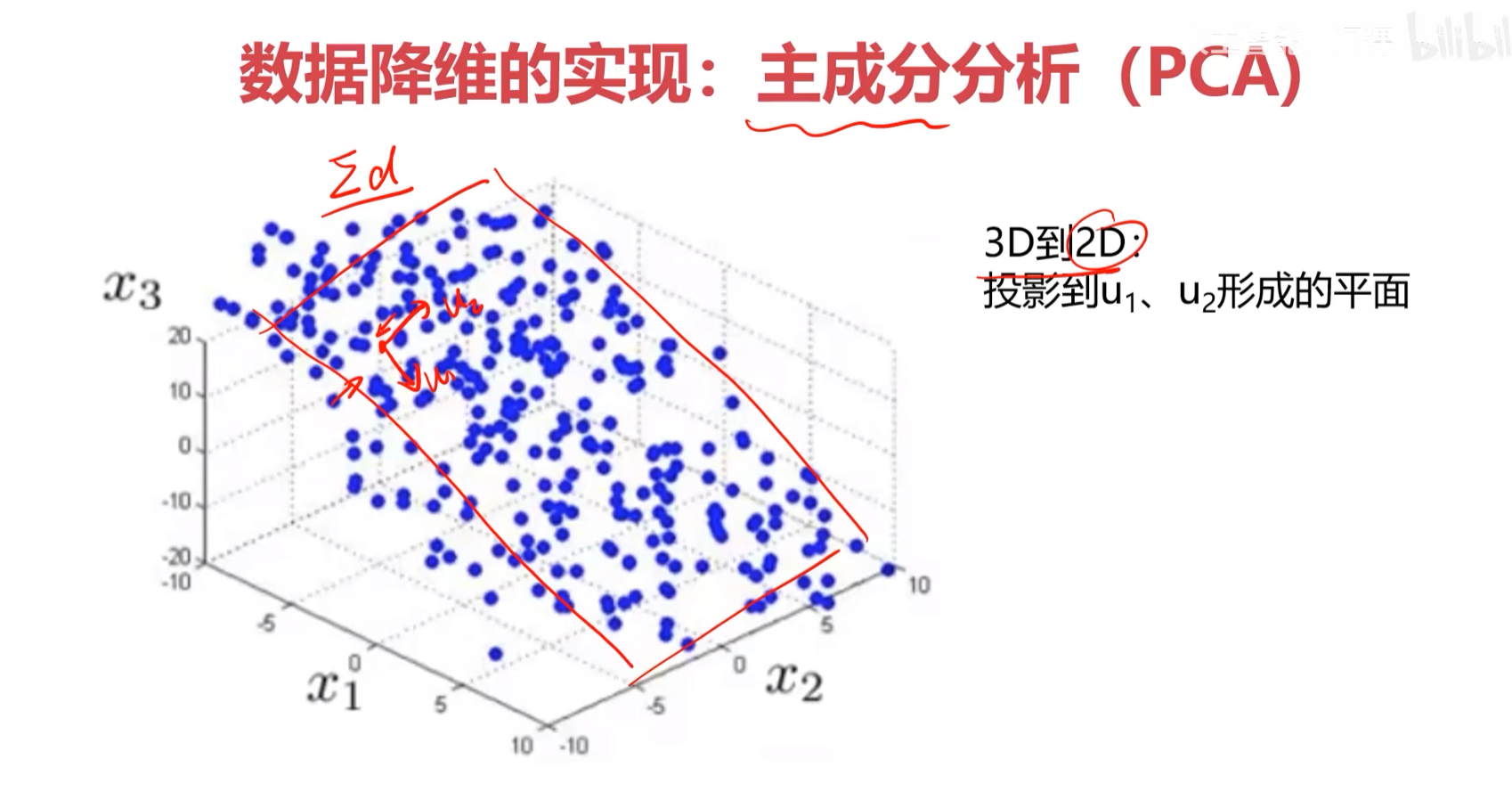
如何保留主要信息:
投影后,不同特征的数据尽可能分得开(即不相关)
如何实现?
使投影后的方差(协方差)最大,因为方差越大,数据越分散

PCA求解与线性回归的区别
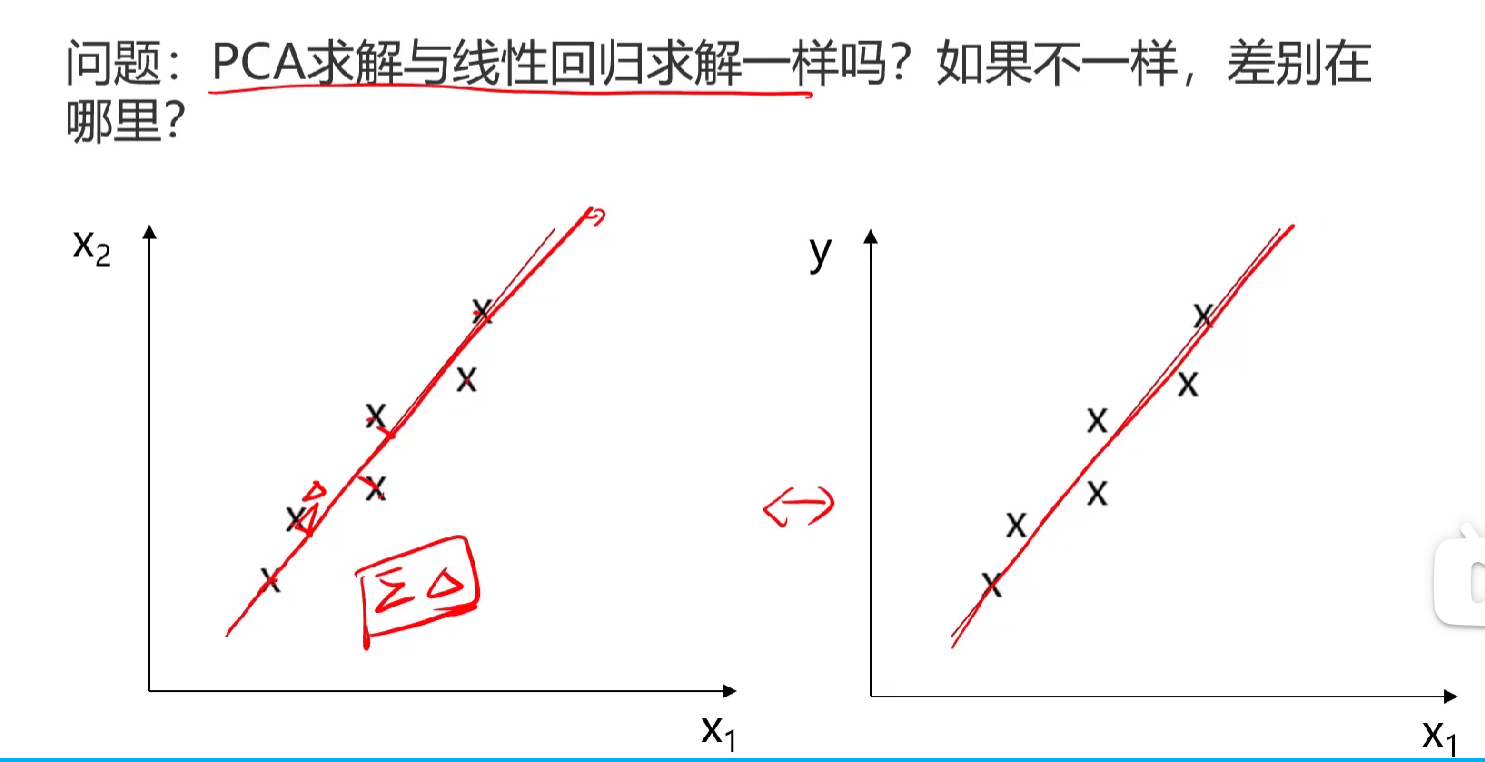
PCA 求解与线性回归求解不一样 ,核心差别在于优化目标和误差定义,可以从图中直观理解:
1. 误差方向不同(最直观的区别)
- 左侧 PCA 图 :误差是样本点到拟合直线的垂直距离(正交投影),目标是最小化所有点到这条线的垂直距离平方和,即最大化数据在这条线上的方差,从而保留最多信息。
- 右侧线性回归图 :误差是样本点到拟合直线的纵向距离(沿 y 轴方向),目标是最小化所有点在 y 轴方向上的预测误差平方和,即最小化预测值与真实值的偏差。
2. 核心目标不同
- PCA(主成分分析) :属于无监督学习,目标是降维、提取特征,不区分自变量和因变量,只关注数据本身的结构,找到能最大程度保留数据方差的方向。
- 线性回归 :属于有监督学习,目标是预测,明确区分自变量 x 和因变量 y,通过拟合直线来根据 x 预测 y。
3. 求解方法不同
- PCA :通过求解协方差矩阵的特征值和特征向量,找到主成分方向,本质是一个特征分解问题。
- 线性回归 :通过最小化均方误差(MSE)求解,本质是一个最小二乘优化问题。
问题:最小化所有点到直线的垂直距离平方和 ,等价于最大化投影后的方差,而这个方向就是 PCA 要找的主成分方向。
1. 几何直观理解
想象平面上有一组数据点(椭圆形),我们要画一条直线,让所有点到这条直线的垂直距离之和尽可能小:
- 如果直线方向选得不好,很多点离直线很远,垂直距离平方和就会很大。
- 当直线刚好沿着数据分布最广的方向(椭圆长轴)时,大部分点都贴近这条直线,垂直距离平方和就会最小。(数据分布最广的方向,数据投影后越离散)
- 同时,数据点在这条直线上的投影会分布得最开,也就是投影方差最大。
所以,"最小化垂直距离平方和" 和 "最大化投影方差" 其实是在找同一条直线。