vector derivatives

Backprop with Vector
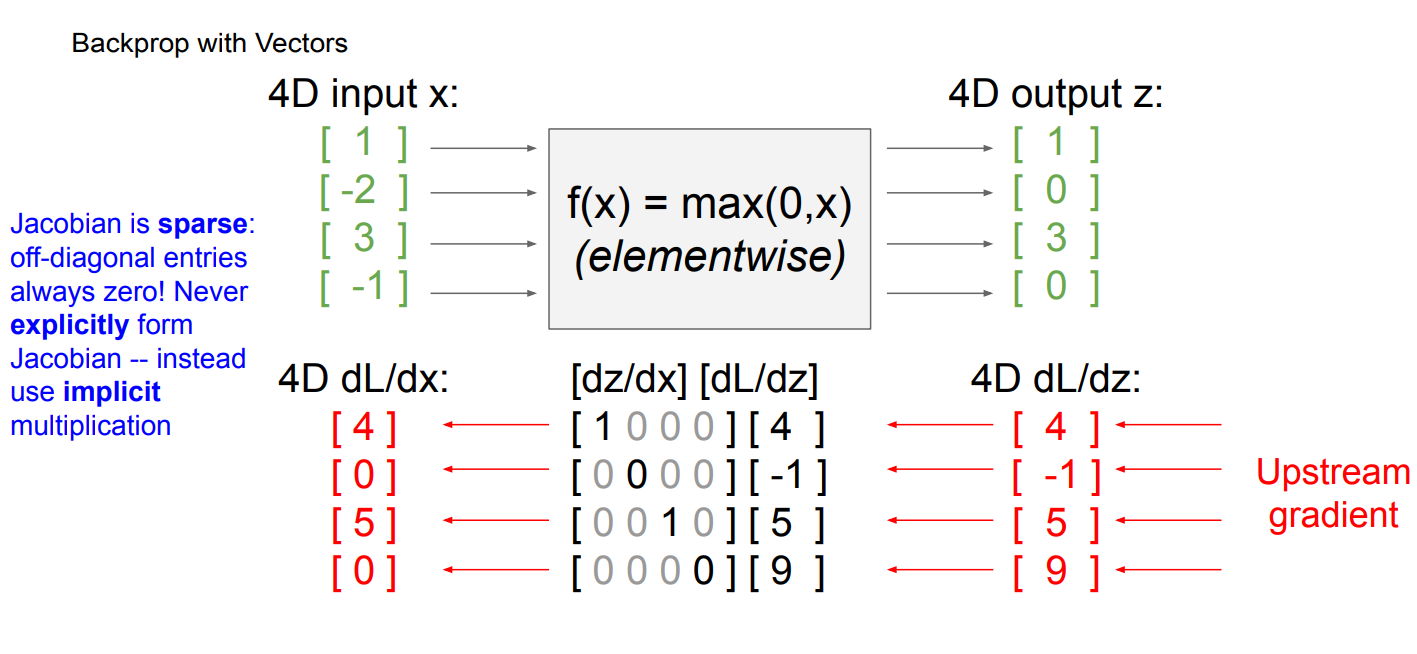
Jocobian用于输出输入均为向量的时候求导
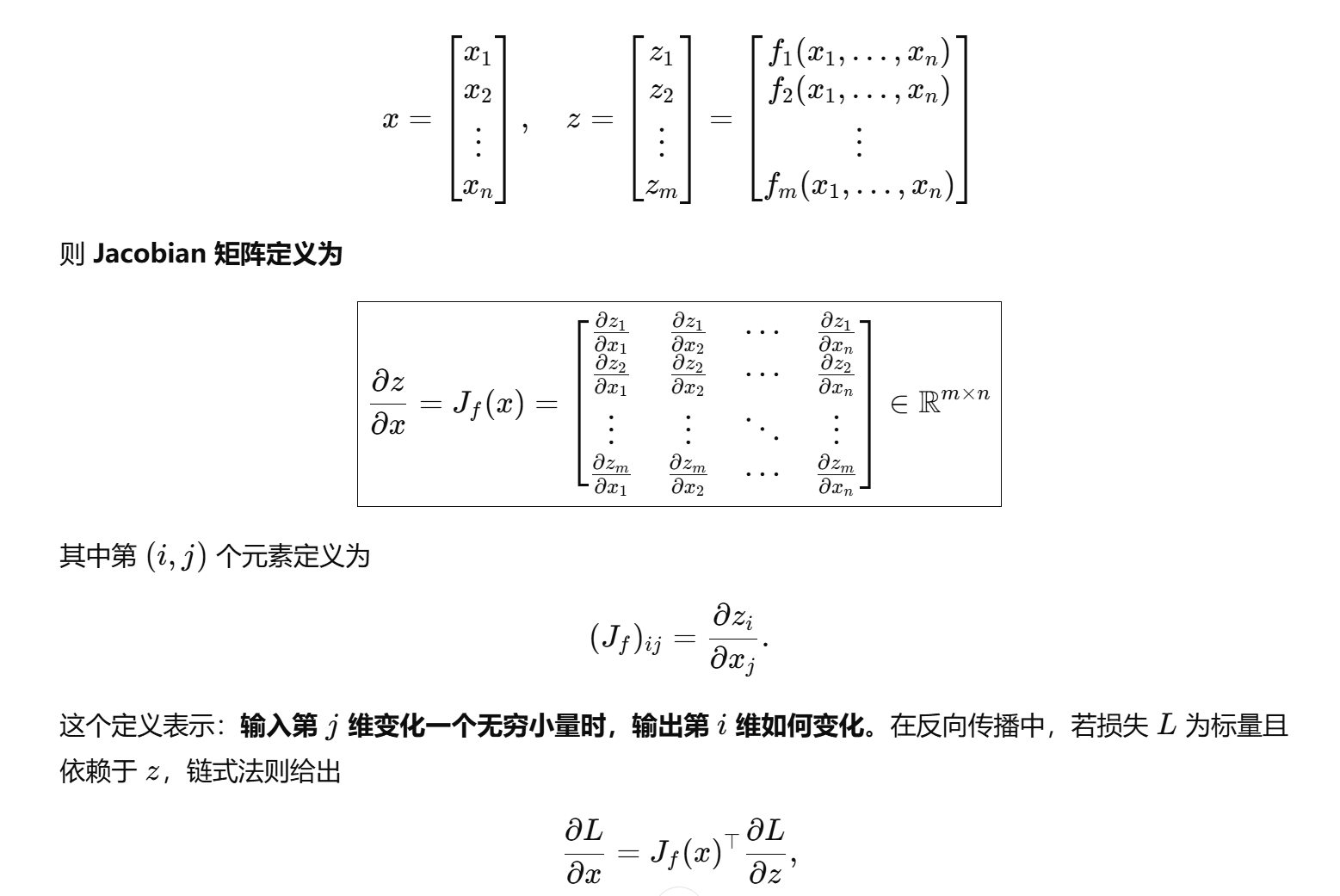
注意方向问题

例子
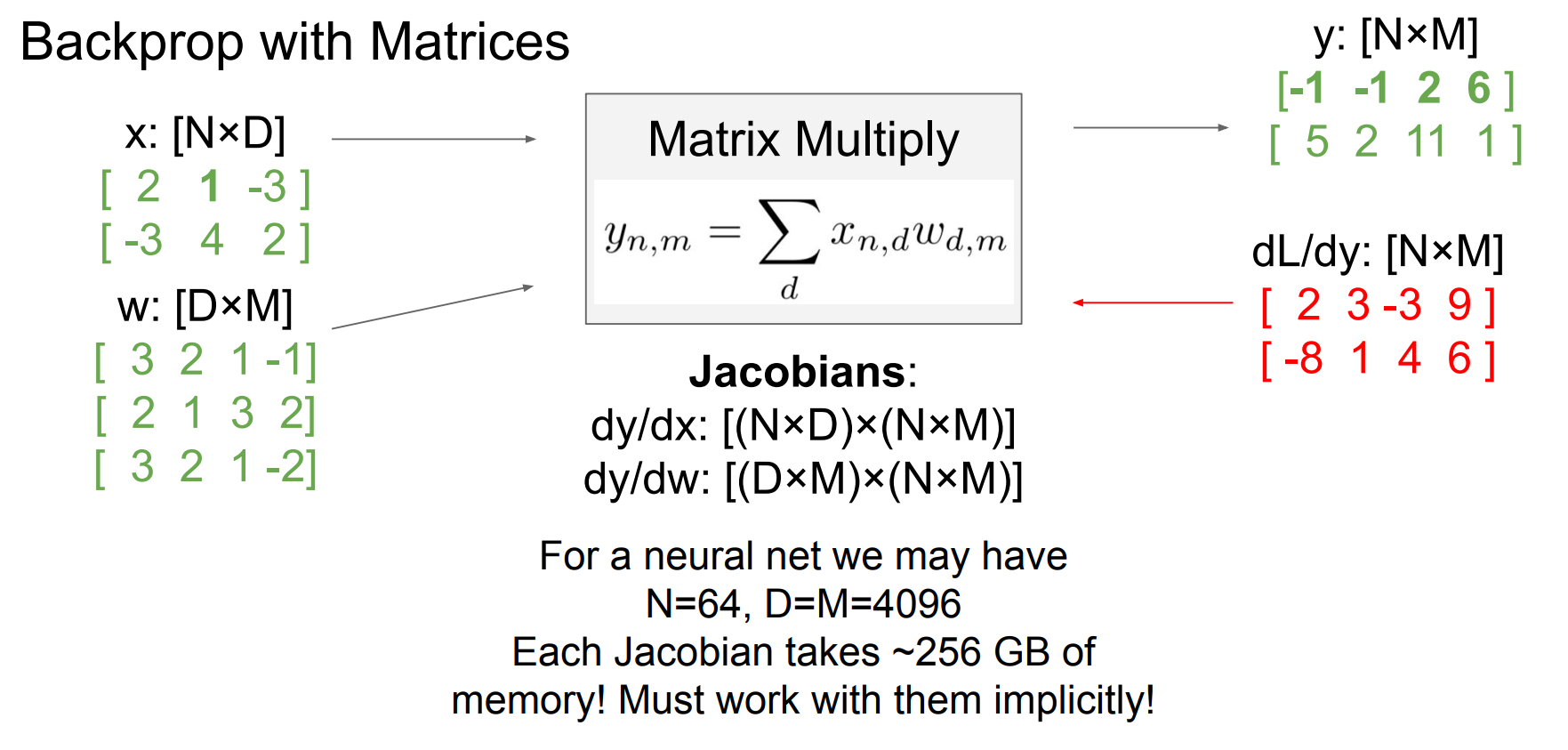
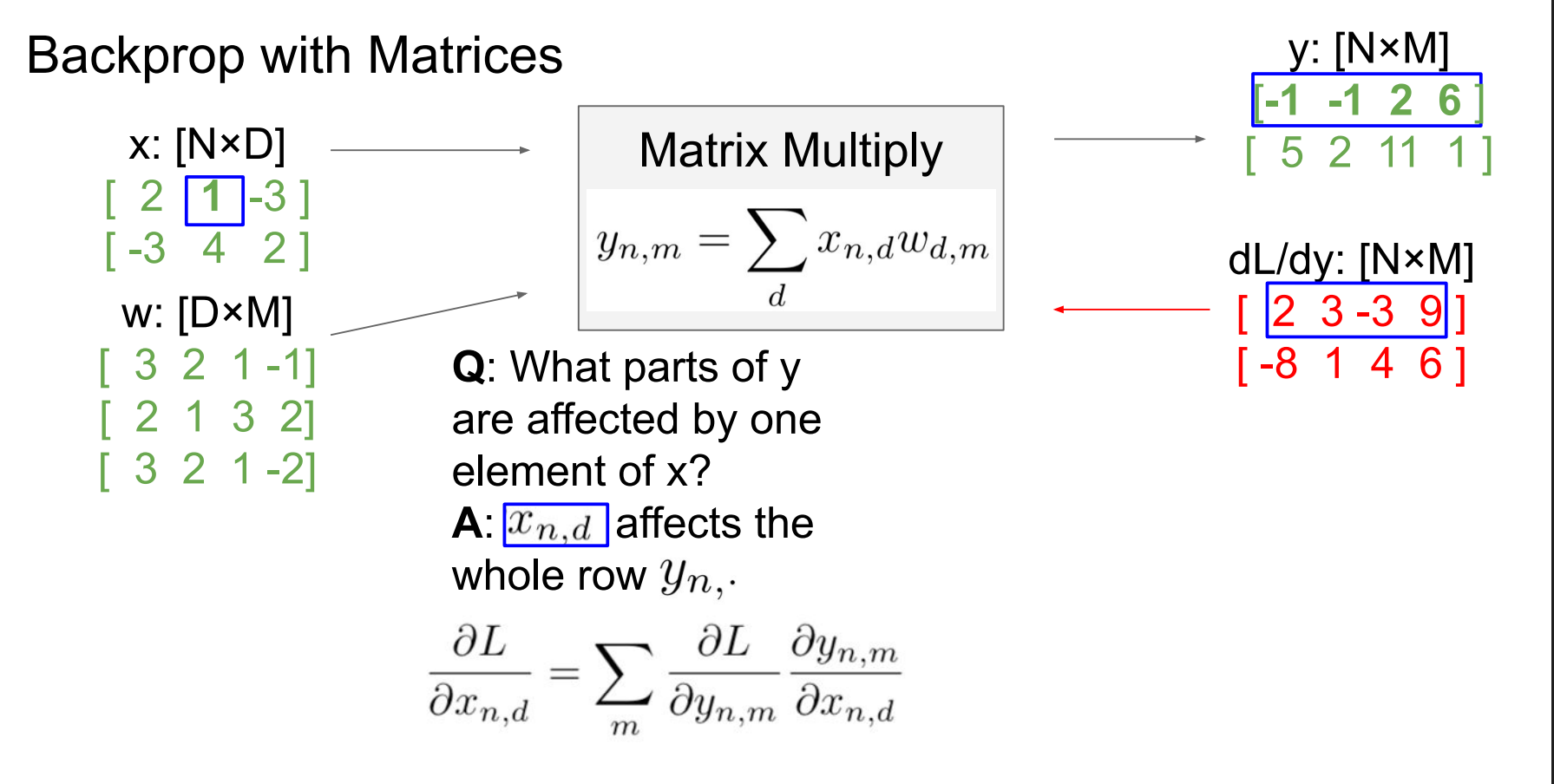
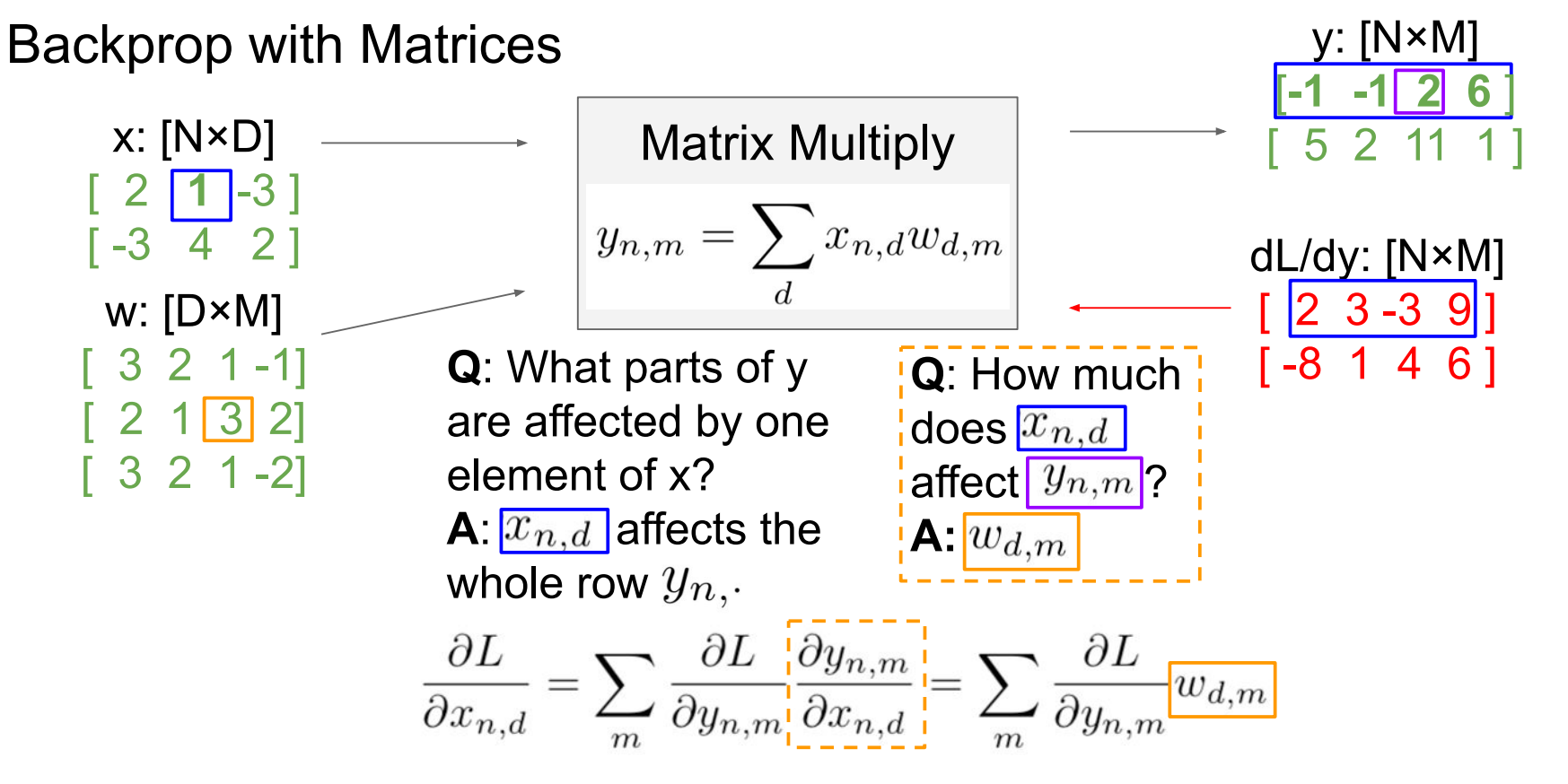
如果只改变一个元素x影响y的什么
-
改变 x1,2x_{1,2}x1,2
-
只影响 y1,1,y1,2,y1,3,y1,4y_{1,1},y_{1,2},y_{1,3},y_{1,4}y1,1,y1,2,y1,3,y1,4
-
所以只用 dL/dydL/dydL/dy 第一行回传
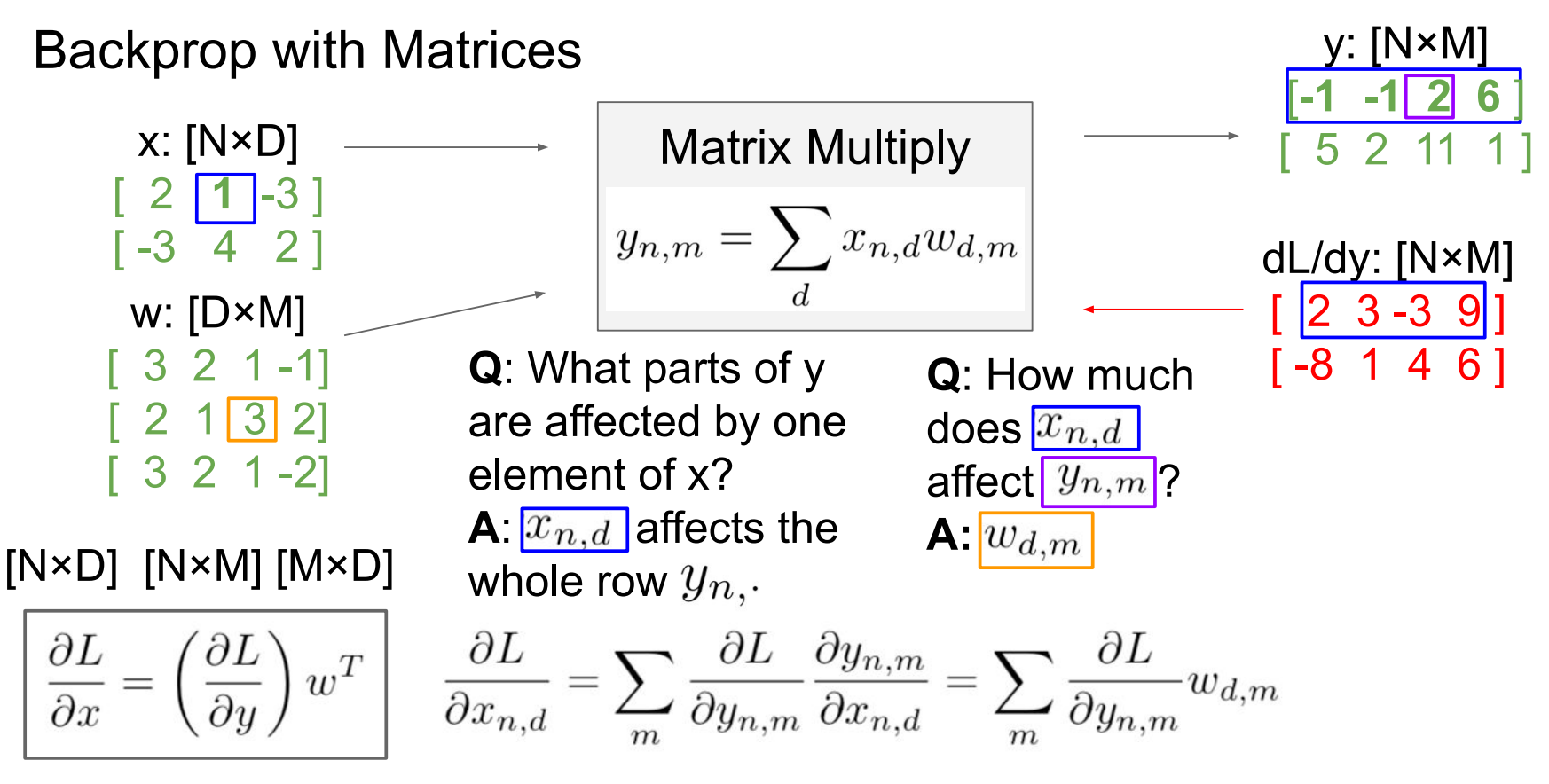
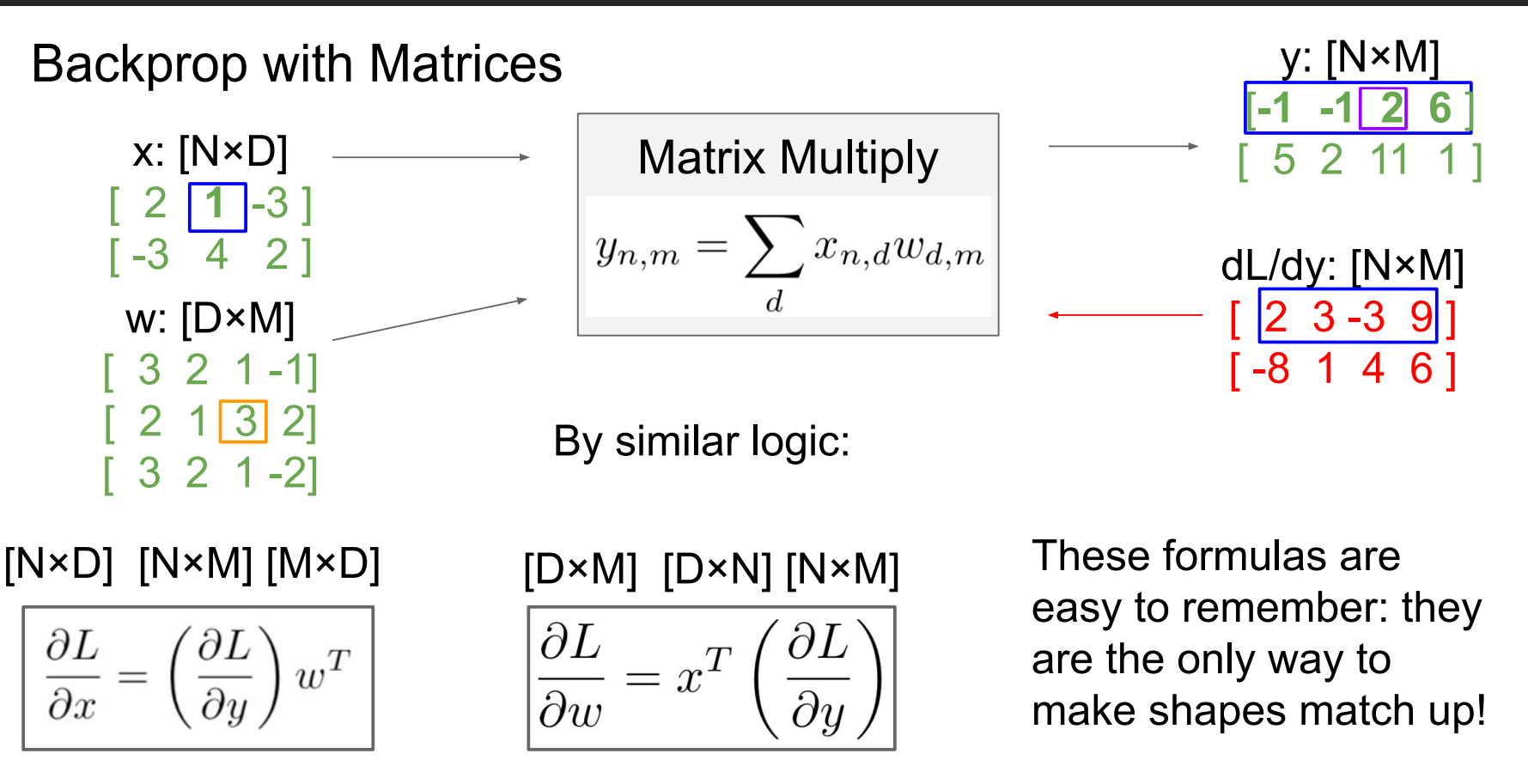
影响多少
Convolutional Neural Networks
Fully Connected Layer
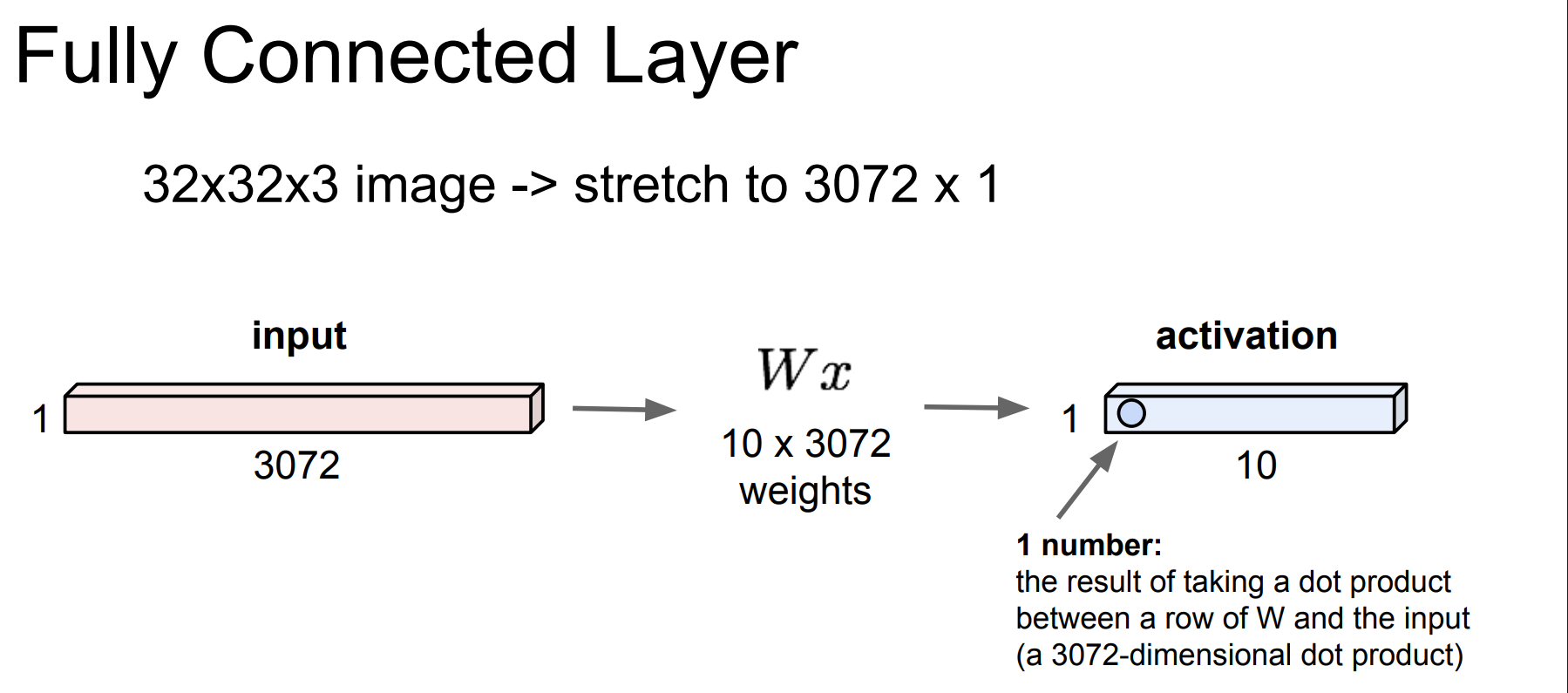
Convolution Layer
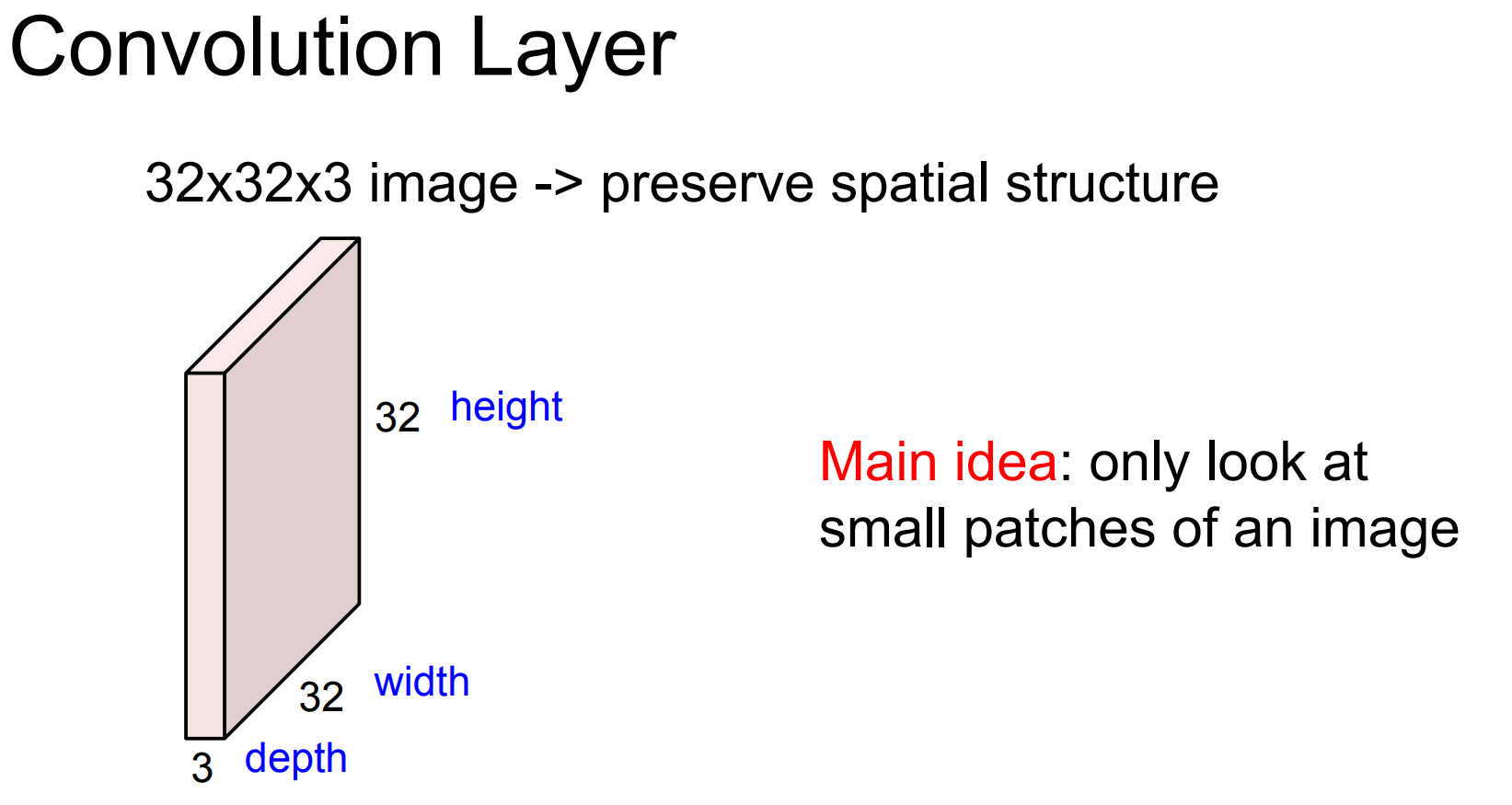
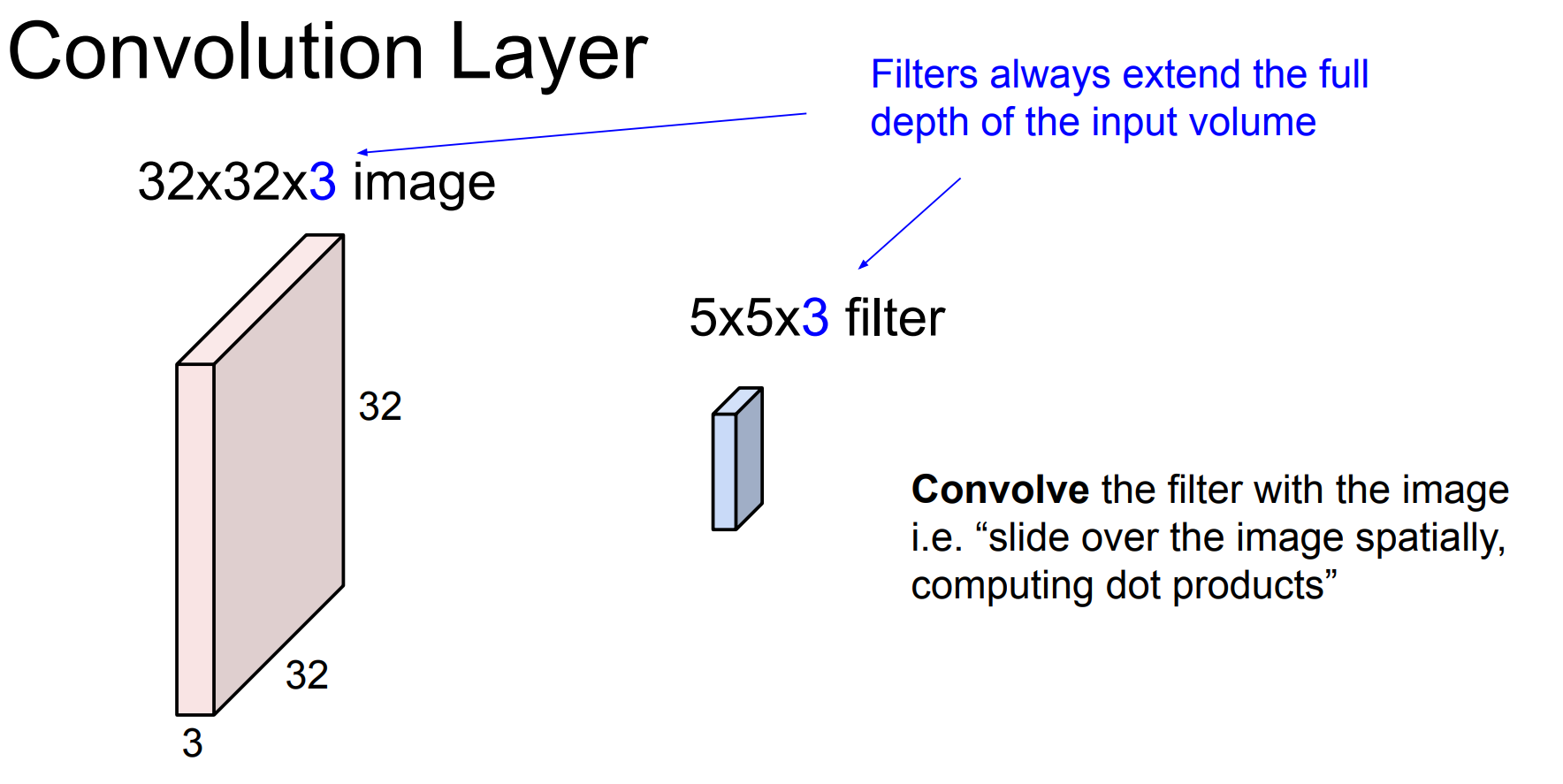
Filter(卷积核)= 一小块可学习的权重参数
它是一个张量:
filter∈Rk×k×C\text{filter} \in \mathbb{R}^{k \times k \times C}filter∈Rk×k×C
-
k×k:空间大小(比如 3×3、5×5)
-
C:输入通道数
-
里面全是可训练参数(weight)
| Fully Connected | Convolution |
|---|---|
| 每个神经元看全图 | 每个神经元只看局部 |
| 参数巨大 | 参数很少 |
| 无空间结构 | 保留空间结构 |
| 无权重共享 | 权重共享 |
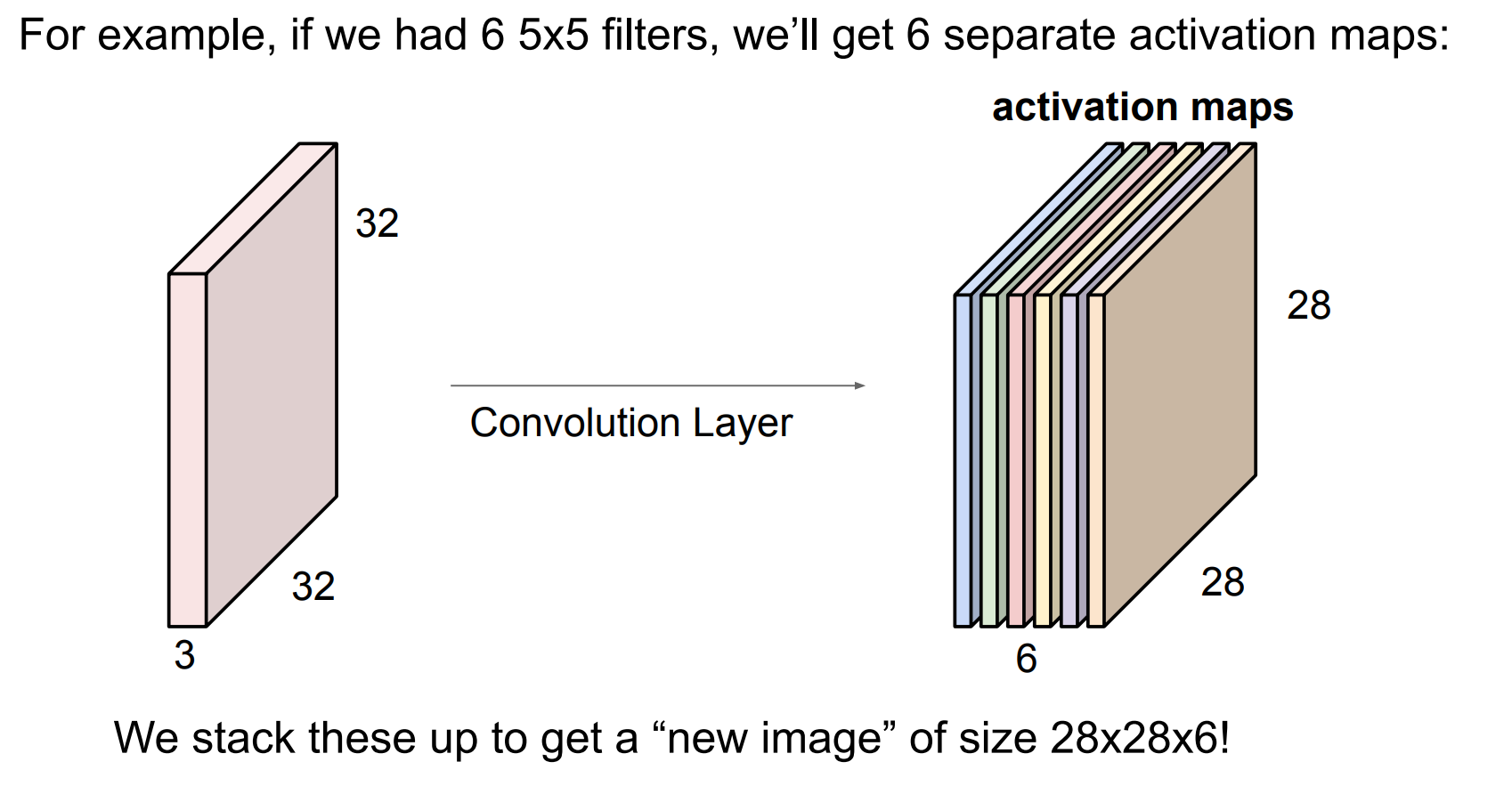
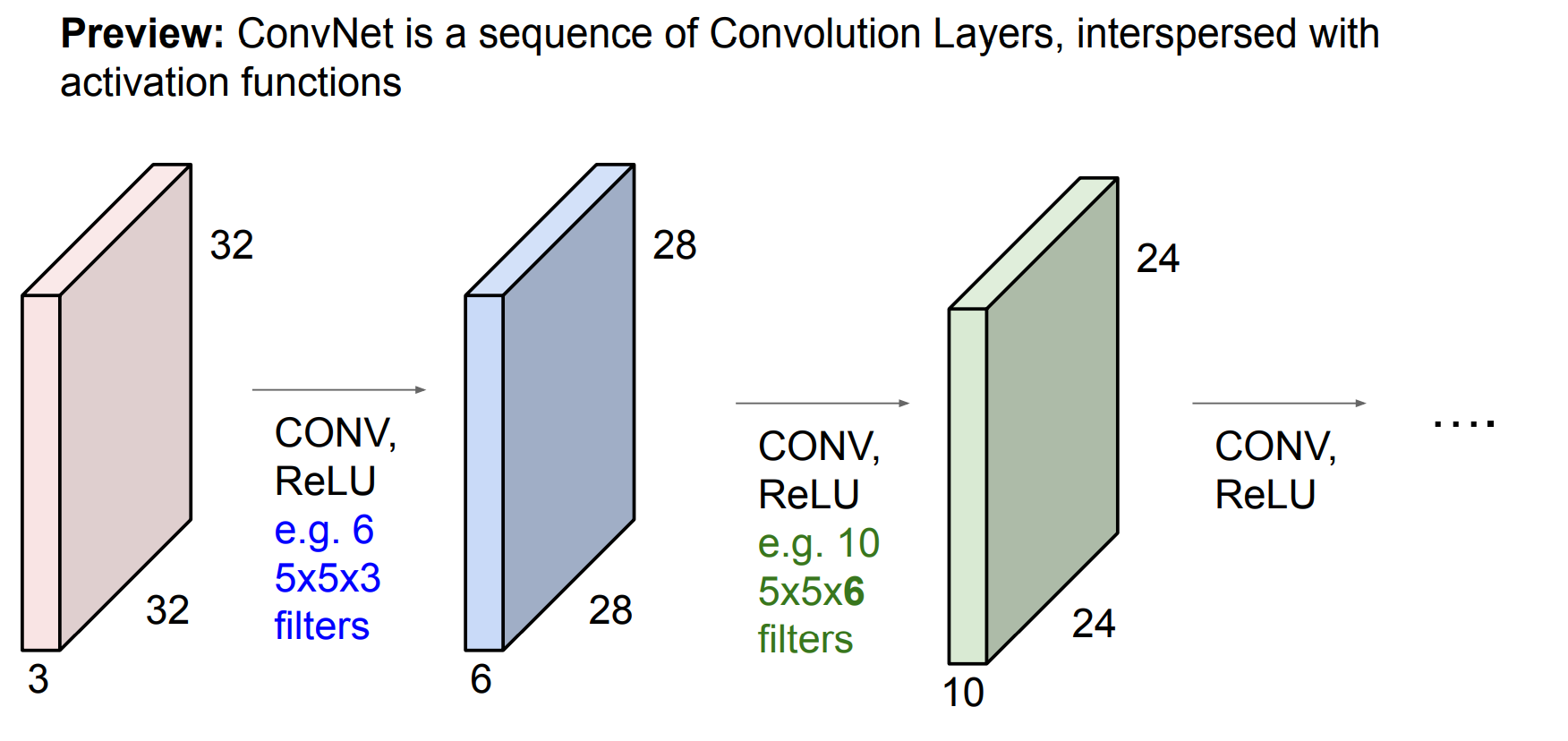
可视化
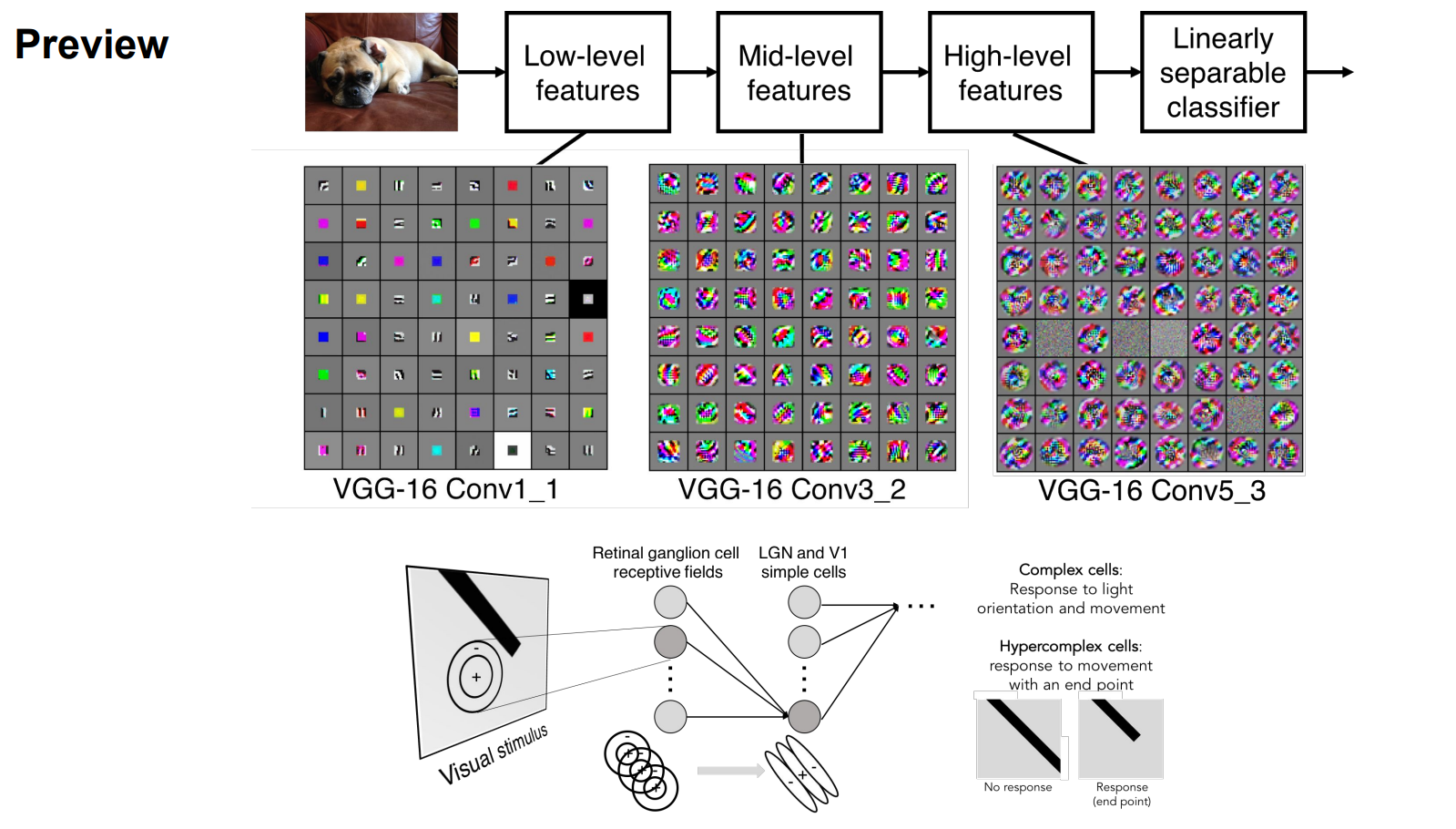
convolution(卷积)
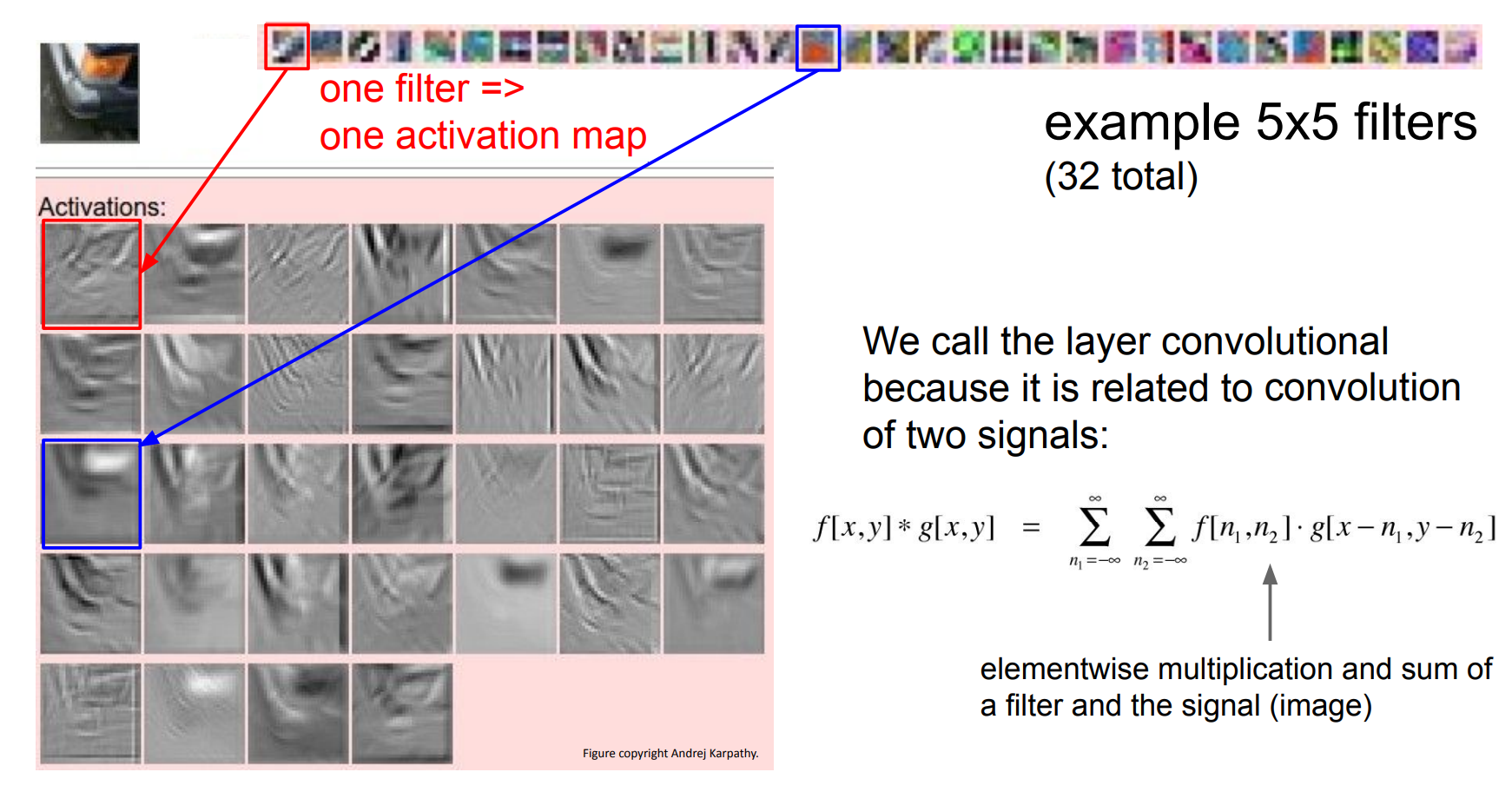
-
有 32 个 5×5 卷积核,一个卷积核是5* 5* 3
-
每个卷积核都会在整张图上滑动(并行的)
-
每个卷积核输出 一张特征图
-
所以得到 32 张 activation maps
卷积的计算过程
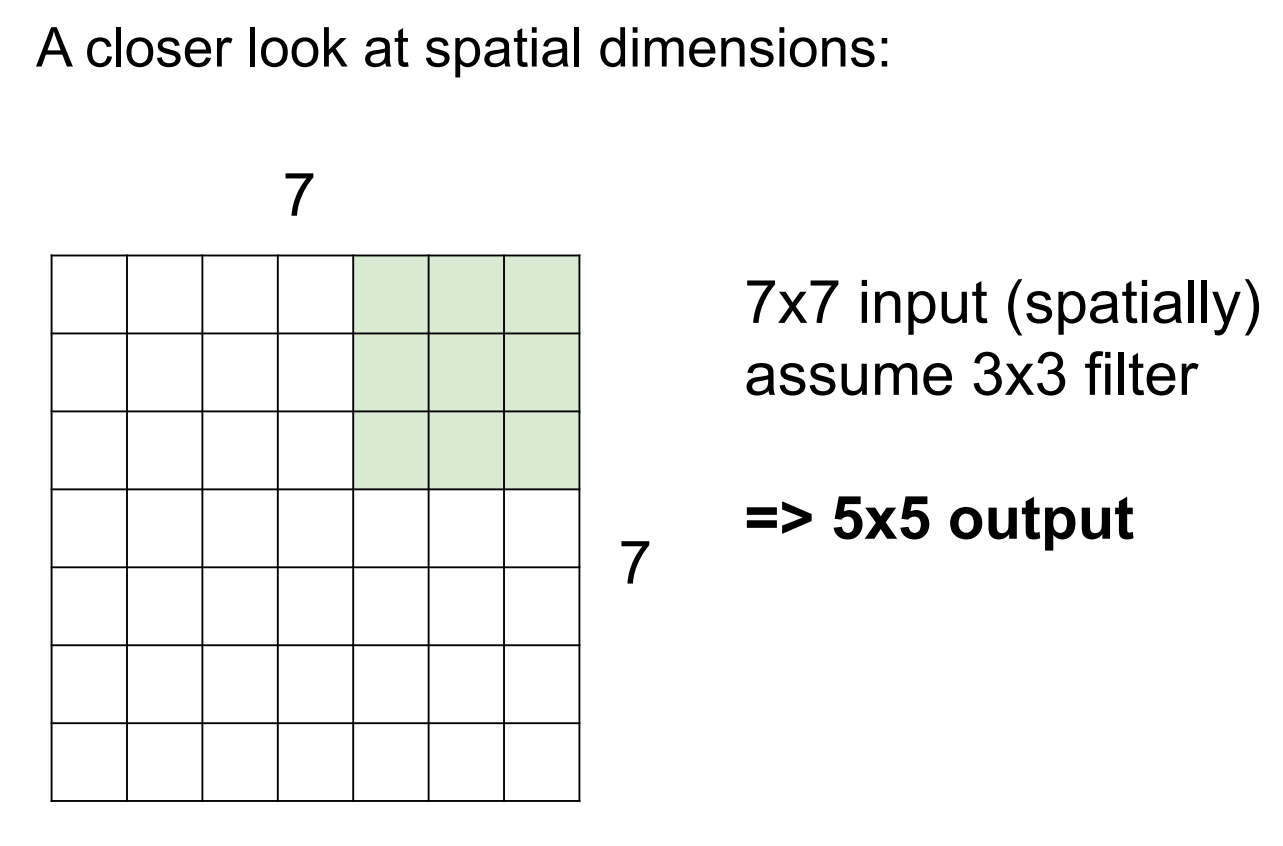
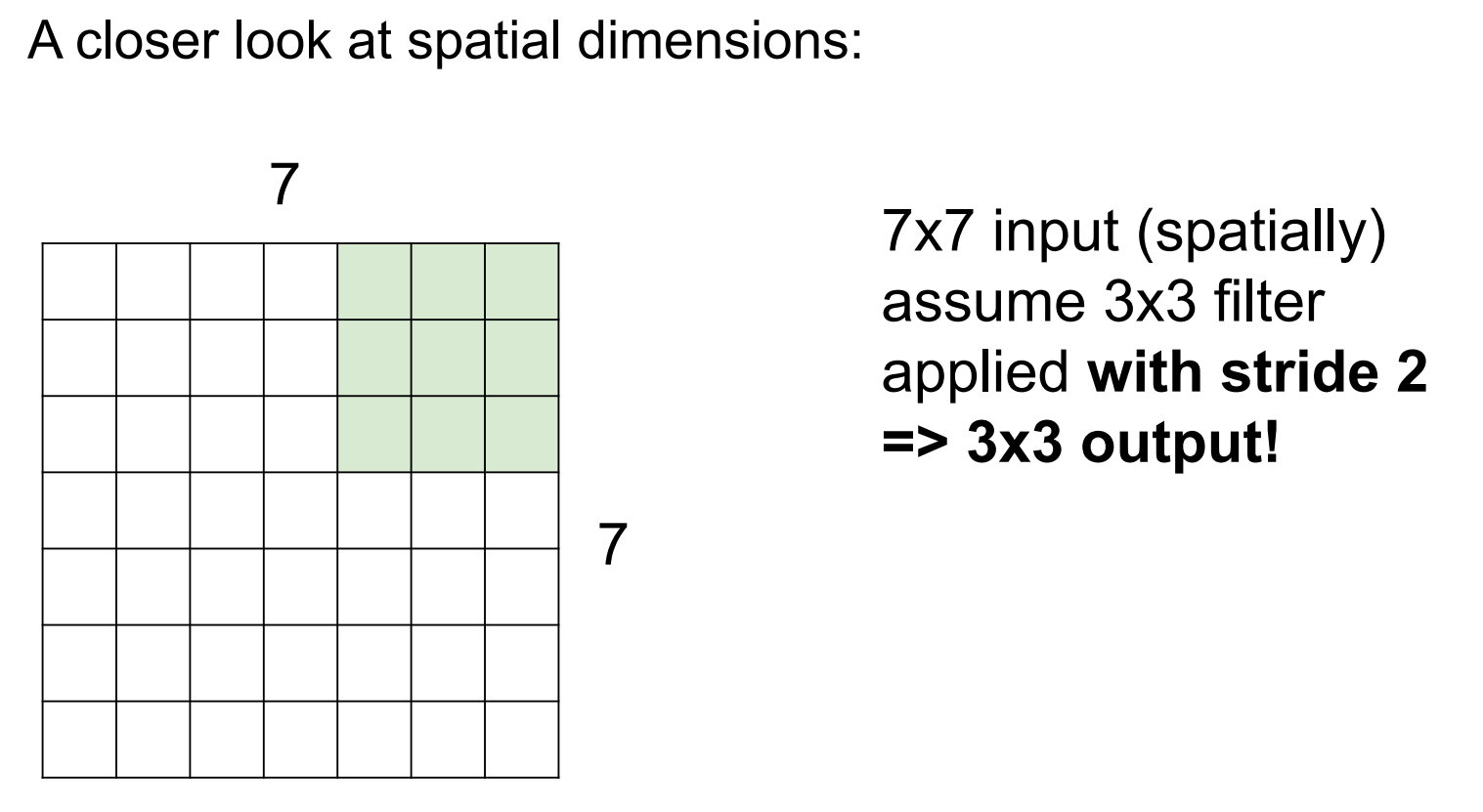
步长为3

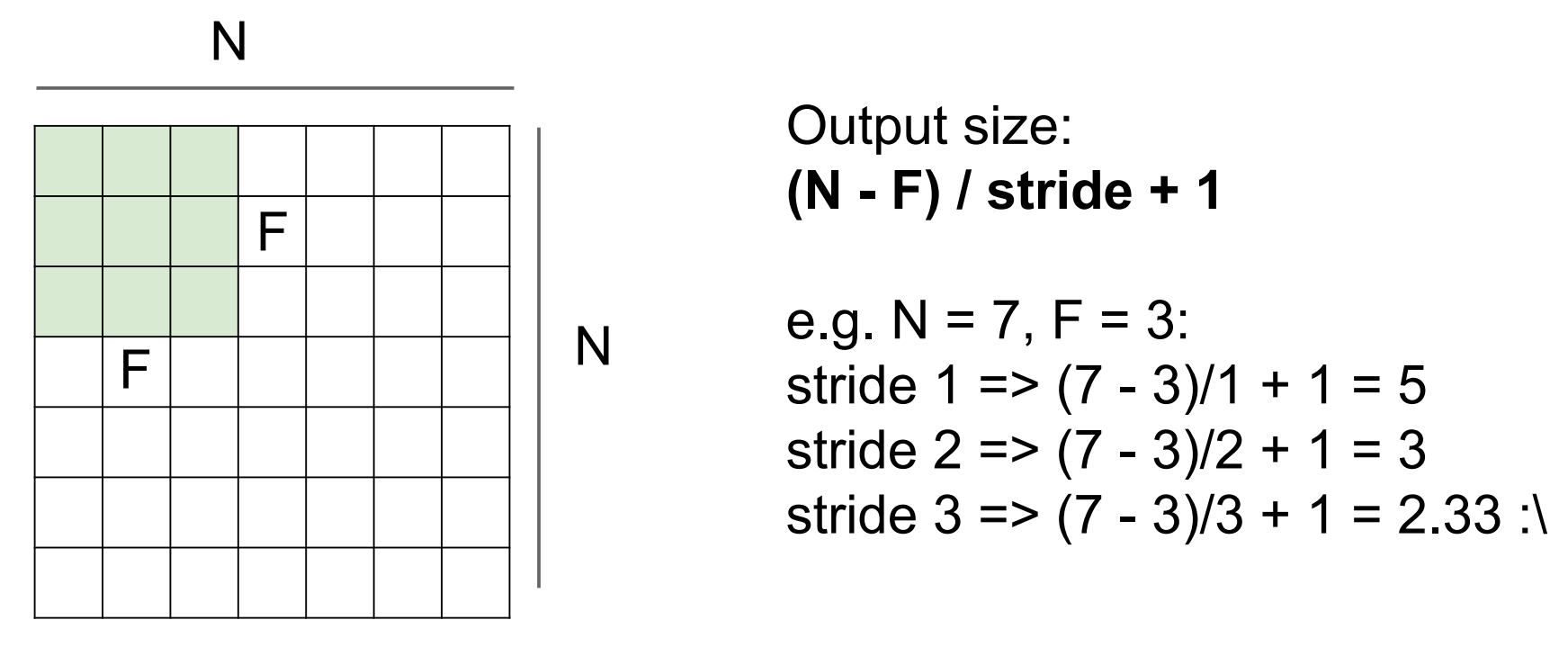
zero padding(零填充)

保持输出尺寸不变
padding = (F − 1) / 2 可以保持尺寸
计算维度
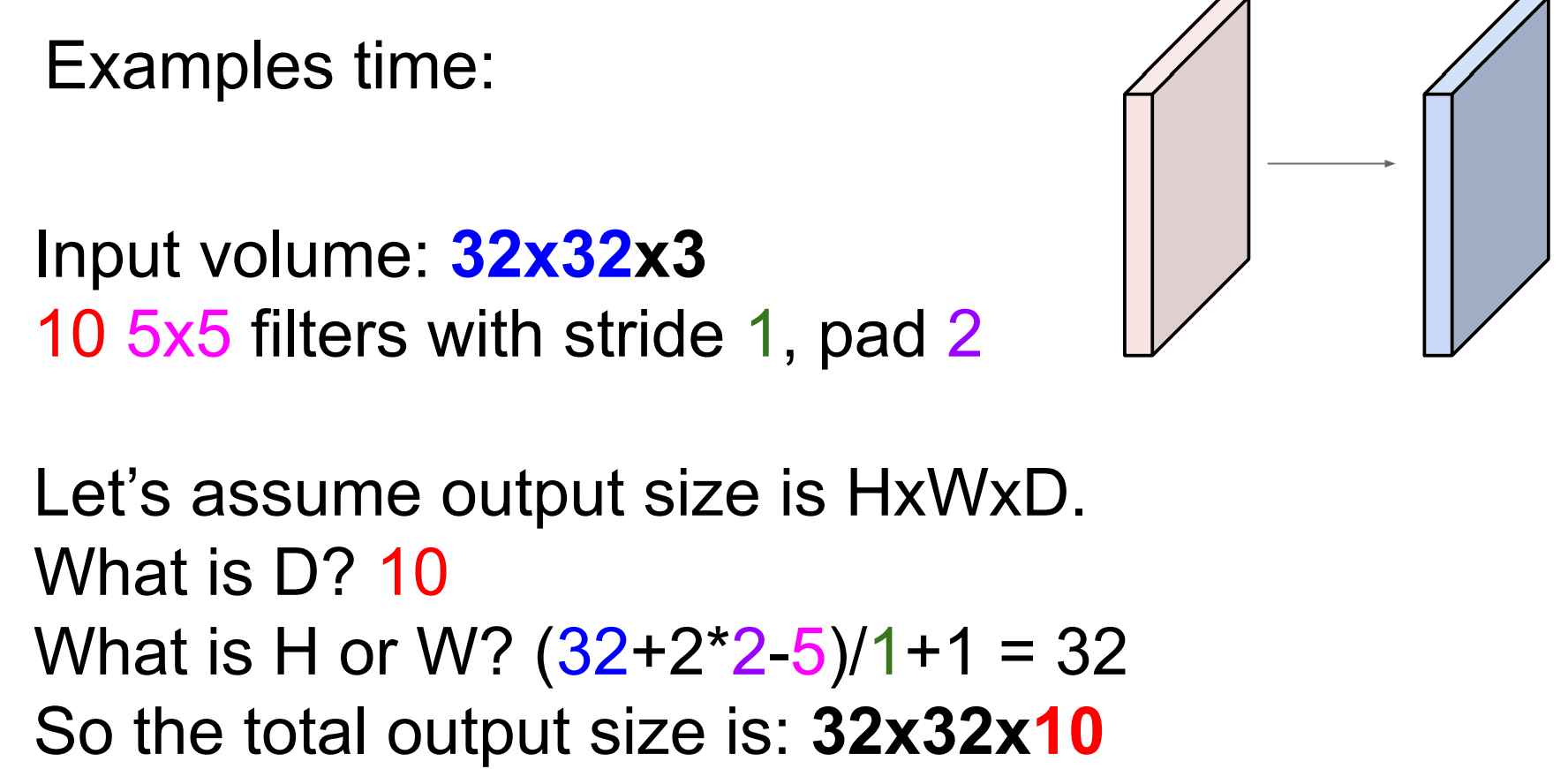
D:10个核 推出输出是10通道
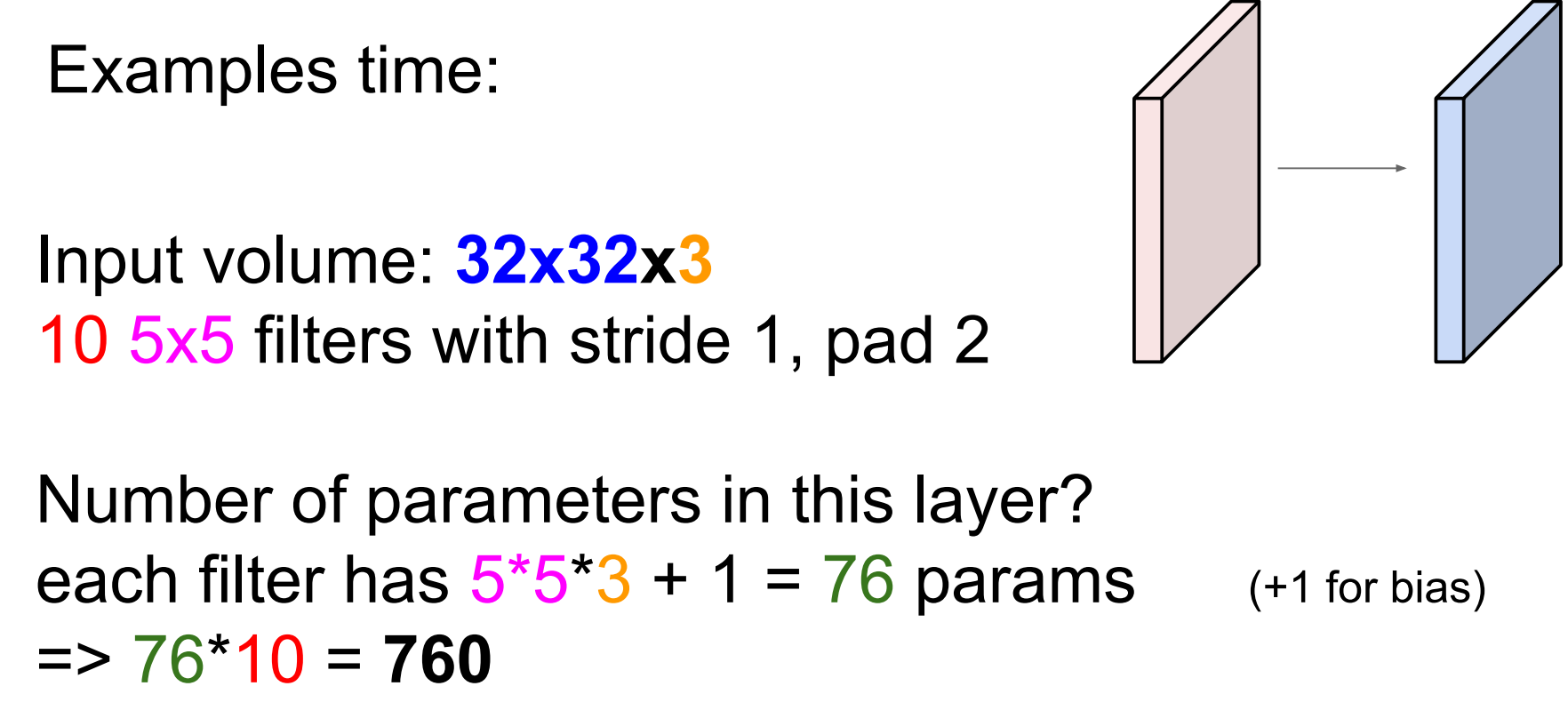
参数数目

每个 filter 一个 bias
1* 1 filter
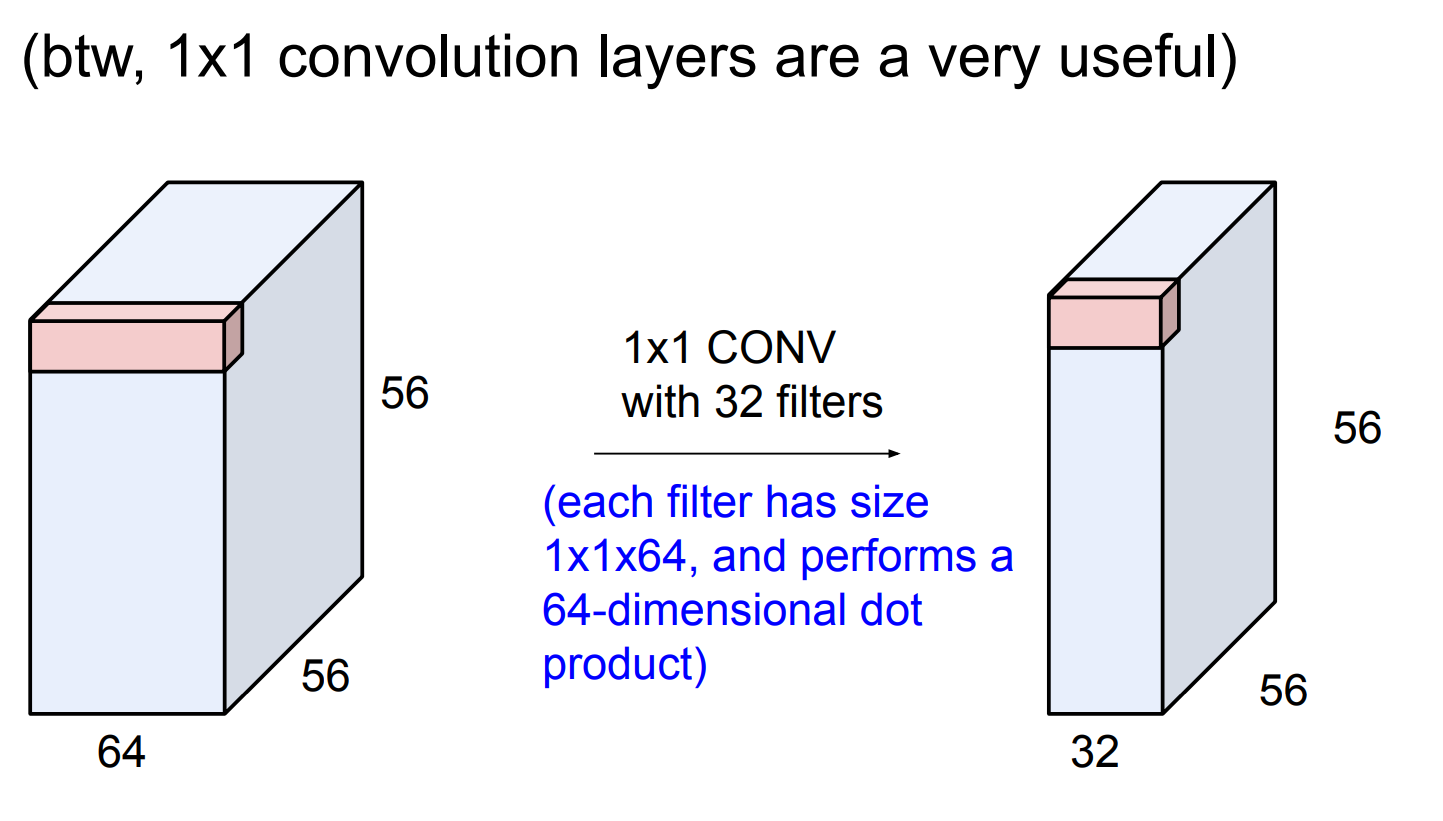
×1 卷积不会看空间,只在每个像素位置做通道线性组合,从而改变通道数并提升表达能力
Pooling layer
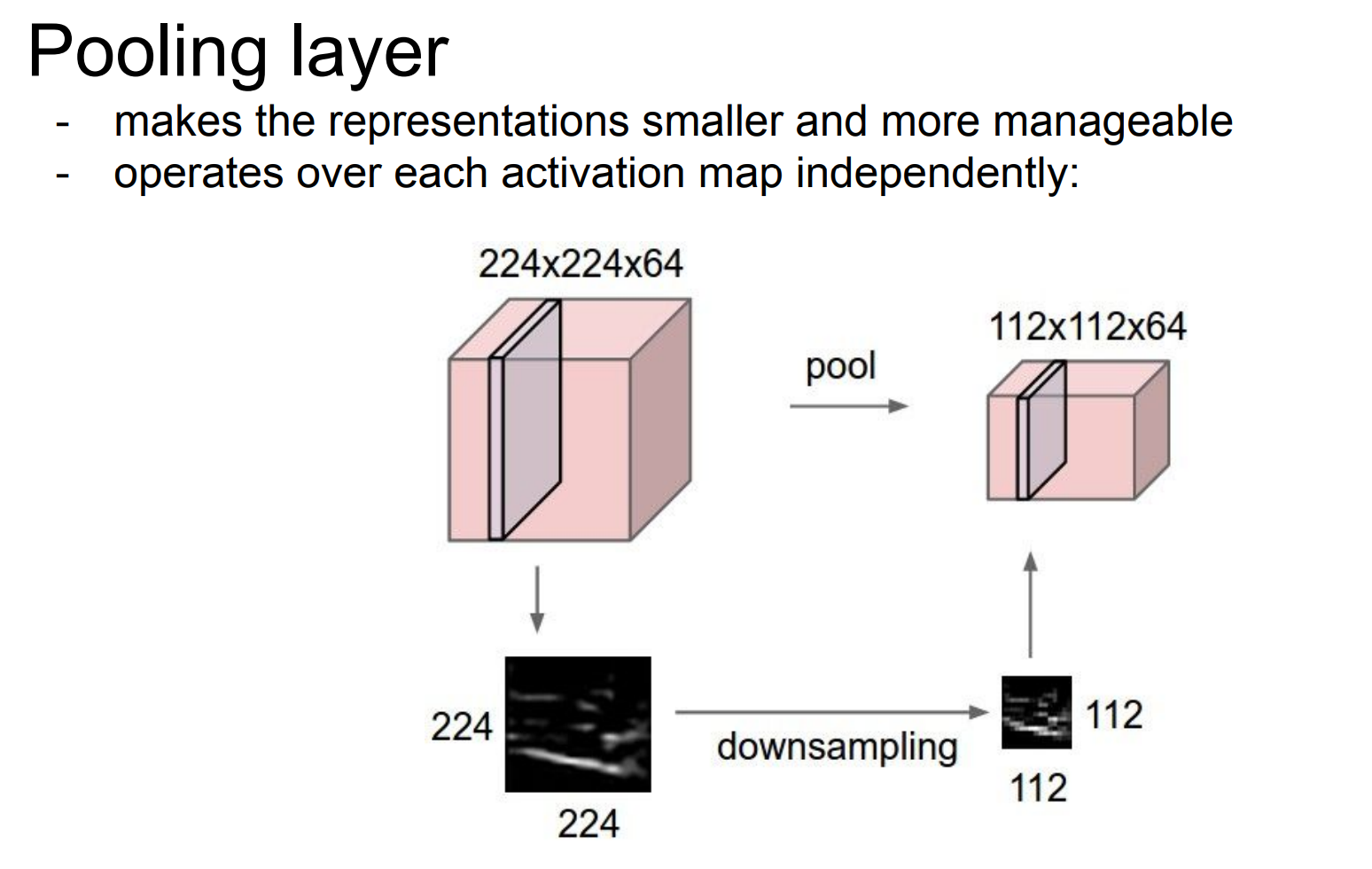
Pooling 对每张特征图独立做下采样,减小空间尺寸、降低计算量,并增强平移不变性
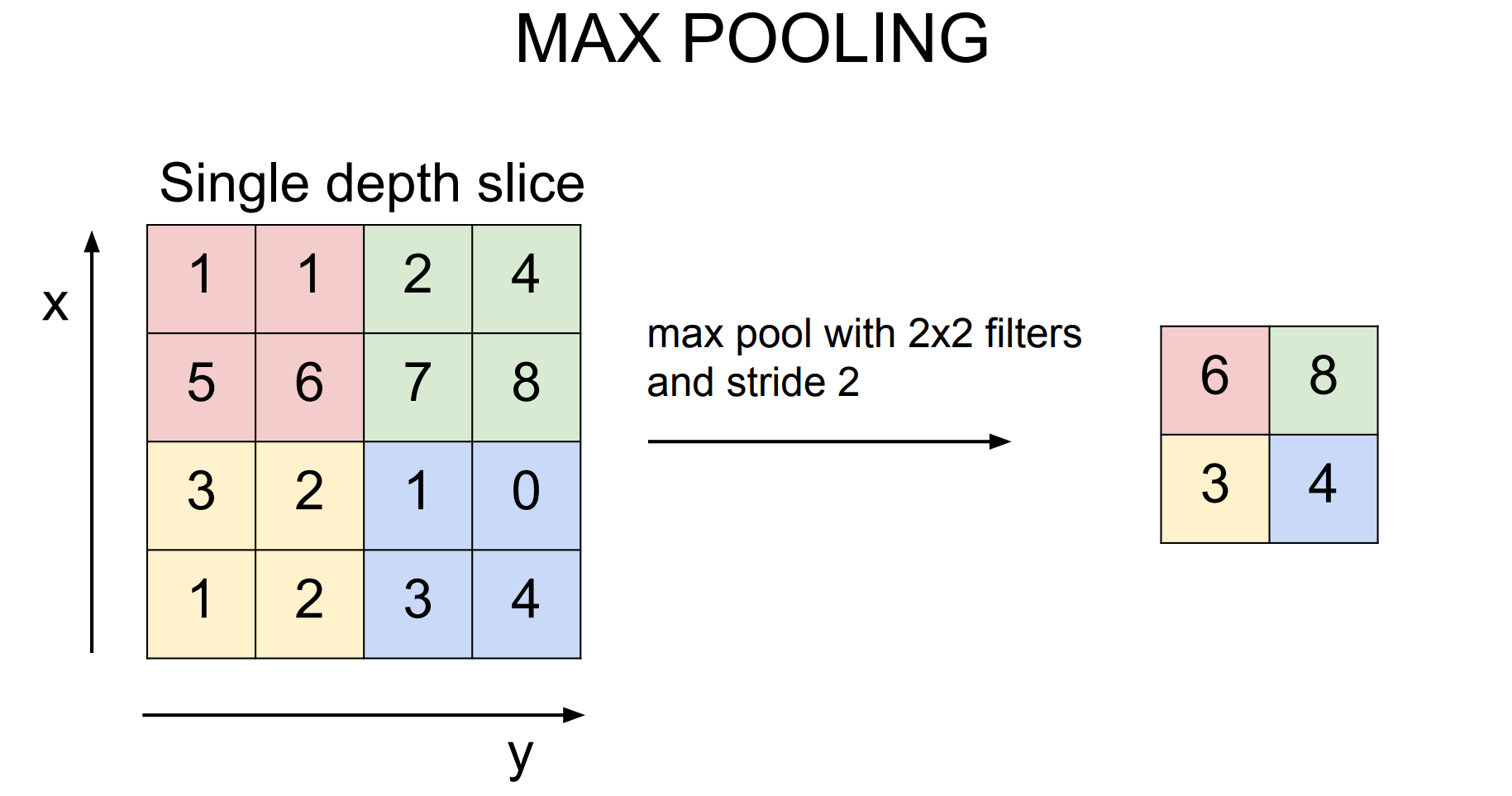

FC layer
