asin和atan2的区别 (CPA指向相关)

背景

在 CPA 零位系（CPA-Zero） 基础上：

绕 y 轴（俯仰轴） 转动角度 𝜃

再绕 z 轴（方位轴） 转动角度 𝜓

你现在有 CPA 零位系下的单位指向矢量：
P=(Px,Py,Pz)T \mathbf{P} = (P_x, P_y, P_z)^\mathsf{T} P=(Px,Py,Pz)T

并且已知 CPA 的几何关系：
{Px=cos⁡θcos⁡ψ Py=sin⁡ψ Pz=−sin⁡θcos⁡ψ \begin{cases} P_x = \cos\theta \cos\psi \ \\ P_y = \sin\psi \ \\ P_z = -\sin\theta \cos\psi \end{cases} ⎩ ⎨ ⎧Px=cosθcosψ Py=sinψ Pz=−sinθcosψ

（1）ψ=sin⁡−1(Py)\psi = \sin^{-1}(P_y)ψ=sin−1(Py)

这是直接利用第二个分量：

只用了 𝑃𝑦=sin𝜓

本质是在 y--z 平面投影里反算 ψ

它的隐含前提是：cosψ≥0, 也就是ψ∈−π/2​,π/2​

（2）

始正切关系式： tan⁡ψ=sin⁡ψcos⁡ψ=PyPx/cos⁡θ \tan \psi = \frac{\sin \psi}{\cos \psi} = \frac{P_y}{P_x / \cos \theta} tanψ=cosψsinψ=Px/cosθPy

简化后得到：tan⁡ψ=Pycos⁡θPx \\tan \\psi = \\frac{P_y \\cos \\theta}{P_x} tanψ=PxPycosθ

使用 atan2 函数完整象限判断的表达式：ψ=atan2⁡(Pycos⁡θ,Px) \\psi = \\operatorname{atan2}(P_y \\cos \\theta, P_x) ψ=atan2(Pycosθ,Px)

输出范围：(−π,π]

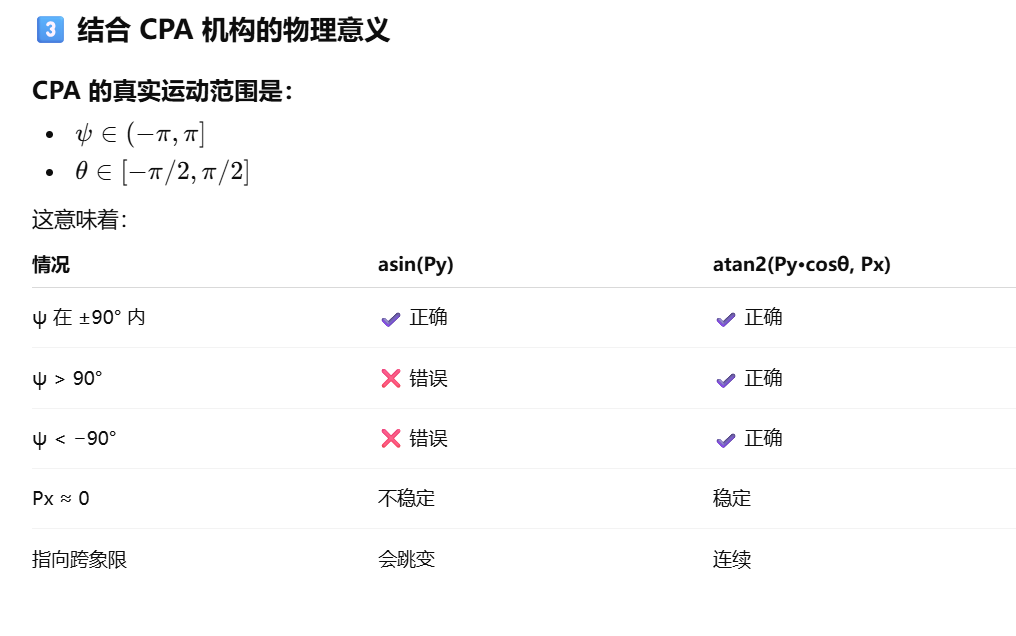
结论

反三角函数只给角度值，atan2 给方向。

所以在姿态 / 指向 / 标定问题里：

永远优先 atan2，除非你能 100% 证明 asin 不会出问题。