本文会继续对反向传播进行讨论,首先会用一个纯数值的例子来展示反向传播的计算过程,然后会上文的如何给苹果\橙子分类例子,构建一个简单的MLP网络来进行分类,加深理解反向传播的全过程。
计算前向传播与反向传播
(这里所有用到的公式,在深度学习的数学原理(三)中有推导)
为了方便手动计算,我们假定如下:
- 输入层:2 个特征(x1,x2),隐藏层:3 个神经元,输出层:1 个神经元
- 单个样本:输入 X=[0.7 0.8],真实标签 y=1(代表 "苹果")
- 初始参数(手动选取便于计算的数值):

- 激活函数:

- 损失函数:二分类交叉熵
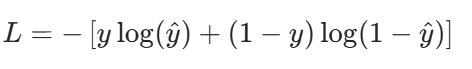
- 学习率 α=0.5
这里有必要说明一下为什么隐藏层权重是一个3×2的矩阵:首先我们规定,隐藏层有三个神经元 ,由于输入层有两个特征,因此如果想做矩阵乘法,那么隐藏层权重必须是3×2;如果有四个神经元呢?权重矩阵就变成了4×2。
权重矩阵的维度设计,本质上是为了满足矩阵乘法的维度约束,同时让每个隐藏层神经元都能独立地对所有输入特征进行线性组合。
前向传播(从输入到预测)
1. 隐藏层线性输出 Z1
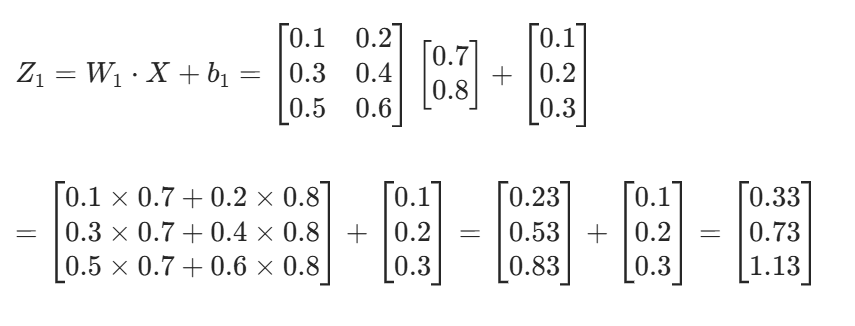
2. 隐藏层激活输出 A1=σ(Z1)

3. 输出层线性输出 Z2
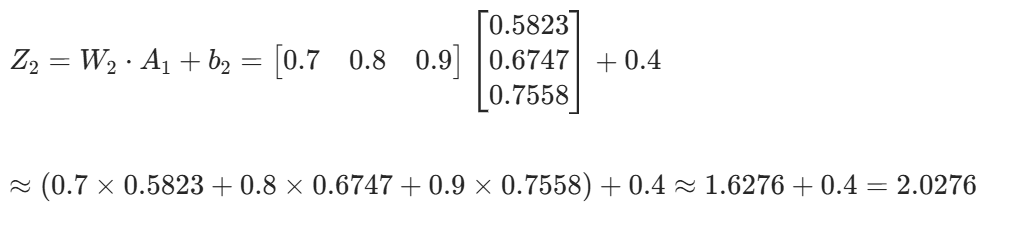
4. 输出层激活输出 A2=σ(Z2)
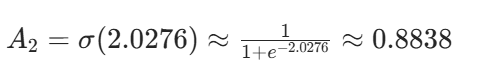
5. 交叉熵损失 L
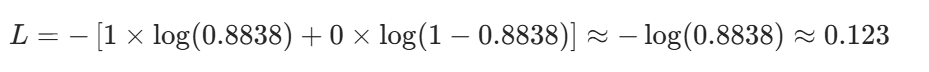
三、反向传播(从损失倒推梯度)
1. 输出层误差项

2. 输出层参数梯度

3. 隐藏层误差项

4. 隐藏层参数梯度
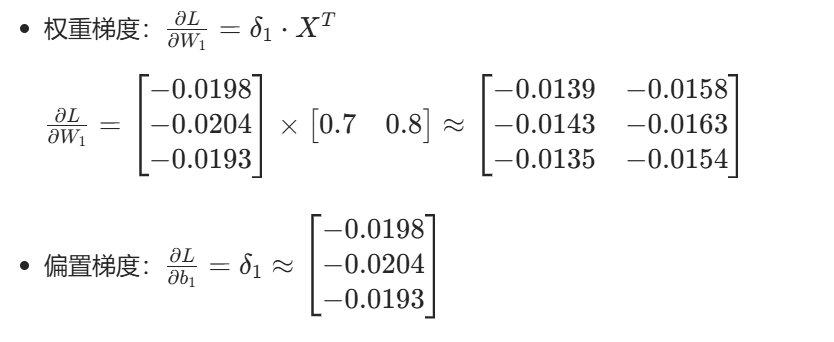
四、参数更新(梯度下降)
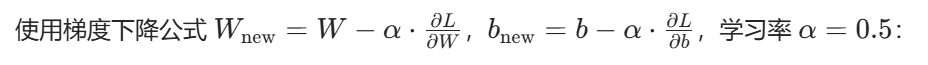
1. 隐藏层参数更新
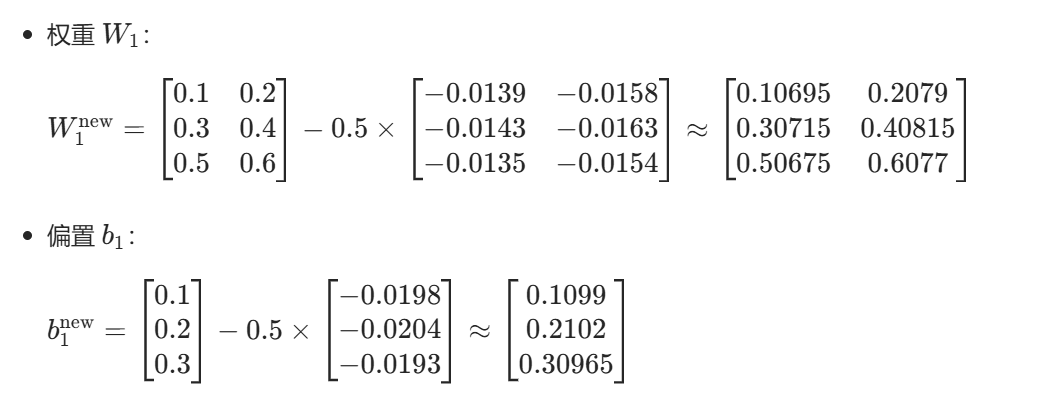
2. 输出层参数更新

经过此轮更新后,Loss会减少,我们反复重复上面的过程,直到Loss无法下降或者达到迭代次数为止,网络中的参数就更新完毕了,网络也就训练好了。
实例------水果分类
下面,我们构建一个和上面数值更新例子完全相同的神经网络,并自己生成一个数据集进行训练,来测试一下网络的效果
1、导入库
python
import numpy as np
import matplotlib.pyplot as plt
# 设置matplotlib参数
plt.rcParams['figure.figsize'] = (12, 8)
plt.rcParams['font.size'] = 12
plt.style.use('seaborn-v0_8')
# 设置中文字体显示
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
print("库导入完成")2、数据生成
我们将生成一个简单的二分类数据集,模拟水果分类问题:根据重量和颜色值判断是否为苹果。数据分布是非线性的,线性模型无法完美分离。
python
# 设置随机种子保证结果可重现
np.random.seed(42)
# 生成水果分类数据集
m = 200 # 样本数量
# 苹果类(标签1):重量较重,颜色较红
apple_weight = np.random.normal(0.7, 0.1, m//2)
apple_color = np.random.normal(0.8, 0.1, m//2)
apple_labels = np.ones(m//2)
# 橙子类(标签0):重量适中,颜色较橙
orange_weight = np.random.normal(0.5, 0.1, m//2)
orange_color = np.random.normal(0.4, 0.1, m//2)
orange_labels = np.zeros(m//2)
# 合并数据
X = np.column_stack([
np.concatenate([apple_weight, orange_weight]),
np.concatenate([apple_color, orange_color])
])
y = np.concatenate([apple_labels, orange_labels])
# 添加一些噪声使分类更具挑战性
noise_indices = np.random.choice(m, size=m//10, replace=False)
y[noise_indices] = 1 - y[noise_indices] # 翻转标签
# 可视化数据
plt.figure(figsize=(10, 6))
plt.scatter(X[y==1, 0], X[y==1, 1], c='red', alpha=0.7, label='苹果', s=50)
plt.scatter(X[y==0, 0], X[y==0, 1], c='orange', alpha=0.7, label='橙子', s=50)
plt.xlabel('重量 (kg)')
plt.ylabel('颜色值 (0-1)')
plt.title('水果分类数据集')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
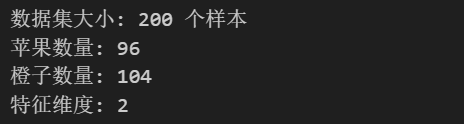
print(f"数据集大小: {m} 个样本")
print(f"苹果数量: {np.sum(y==1)}")
print(f"橙子数量: {np.sum(y==0)}")
print(f"特征维度: {X.shape[1]}")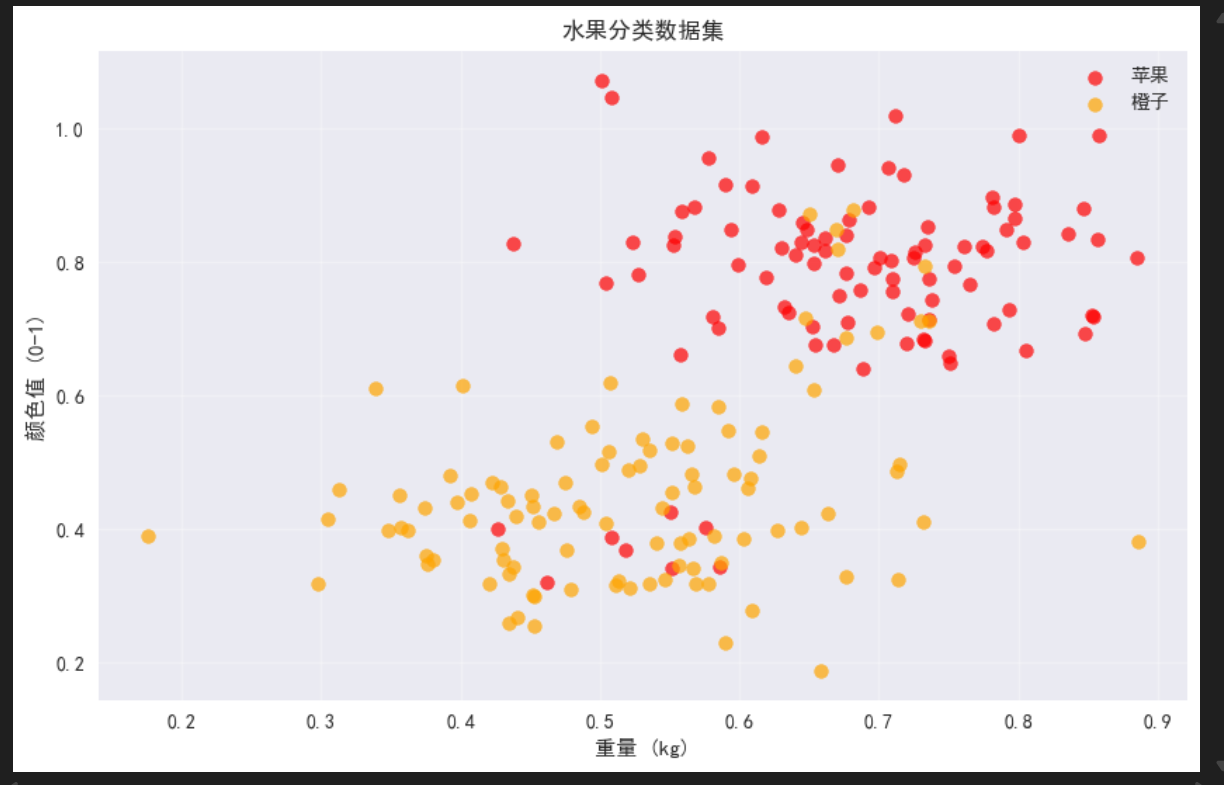
可以看到,颜色越大(深)重量越大,越可能是苹果,当然橙子也有可能颜色很深或者重量很大,这是符号实际情况的
3、实现简单神经网络
python
class SimpleNeuralNetwork:
"""
简单的两层神经网络实现
"""
def __init__(self, input_size, hidden_size, output_size):
"""
初始化网络参数
参数:
input_size: 输入层大小
hidden_size: 隐藏层大小
output_size: 输出层大小
"""
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
# 初始化权重和偏置
self.W1 = np.random.randn(hidden_size, input_size) * 0.1
self.b1 = np.zeros((hidden_size, 1))
self.W2 = np.random.randn(output_size, hidden_size) * 0.1
self.b2 = np.zeros((output_size, 1))
def sigmoid(self, z):
"""Sigmoid激活函数"""
return 1 / (1 + np.exp(-z))
def sigmoid_derivative(self, z):
"""Sigmoid导数"""
s = self.sigmoid(z)
return s * (1 - s)
def forward(self, X):
"""
前向传播
参数:
X: 输入数据 (n_features, m)
返回:
A2: 输出层激活值
cache: 缓存中间结果用于反向传播
"""
# 隐藏层
Z1 = np.dot(self.W1, X) + self.b1
A1 = self.sigmoid(Z1)
# 输出层
Z2 = np.dot(self.W2, A1) + self.b2
A2 = self.sigmoid(Z2)
cache = {
'Z1': Z1, 'A1': A1,
'Z2': Z2, 'A2': A2,
'X': X
}
return A2, cache
def backward(self, A2, y, cache):
"""
反向传播
参数:
A2: 输出层激活值
y: 真实标签
cache: 前向传播缓存
返回:
grads: 梯度字典
"""
m = y.shape[1]
# 输出层梯度
dZ2 = A2 - y
dW2 = np.dot(dZ2, cache['A1'].T) / m
db2 = np.sum(dZ2, axis=1, keepdims=True) / m
# 隐藏层梯度
dZ1 = np.dot(self.W2.T, dZ2) * self.sigmoid_derivative(cache['Z1'])
dW1 = np.dot(dZ1, cache['X'].T) / m
db1 = np.sum(dZ1, axis=1, keepdims=True) / m
grads = {
'dW1': dW1, 'db1': db1,
'dW2': dW2, 'db2': db2
}
return grads
def update_parameters(self, grads, learning_rate):
"""
更新参数
参数:
grads: 梯度字典
learning_rate: 学习率
"""
self.W1 -= learning_rate * grads['dW1']
self.b1 -= learning_rate * grads['db1']
self.W2 -= learning_rate * grads['dW2']
self.b2 -= learning_rate * grads['db2']
def compute_loss(self, A2, y):
"""
计算交叉熵损失
参数:
A2: 预测输出
y: 真实标签
返回:
loss: 损失值
"""
m = y.shape[1]
loss = -np.sum(y * np.log(A2 + 1e-8) + (1 - y) * np.log(1 - A2 + 1e-8)) / m
return loss
def predict(self, X):
"""
预测函数
参数:
X: 输入数据 (n_features, m)
返回:
predictions: 预测结果 (0或1)
"""
A2, _ = self.forward(X)
predictions = (A2 > 0.5).astype(int)
return predictions
# 创建网络实例
input_size = 2 # 重量和颜色
hidden_size = 3 # 隐藏层神经元数量
output_size = 1 # 二分类输出
nn = SimpleNeuralNetwork(input_size, hidden_size, output_size)
print(f"网络结构: 输入层{input_size} -> 隐藏层{hidden_size} -> 输出层{output_size}")
# 测试前向传播
X_test = X[:5].T # 转置为 (n_features, m)
y_test = y[:5].reshape(1, -1)
A2_test, cache_test = nn.forward(X_test)
loss_test = nn.compute_loss(A2_test, y_test)
print(f"测试样本数量: {X_test.shape[1]}")
print(f"初始预测输出: {A2_test.flatten()}")
print(f"真实标签: {y_test.flatten()}")
print(f"初始损失: {loss_test:.4f}")输出如下:

本文实际上手搓了一个神经网络,目前神经网络已经封装的非常好了,无论是网络结构还是损失函数,包括还为介绍到的优化器等,只需要几行代码就能实现。本文为了展示原理,做了一些在实际项目中不是很有必要的工作。
4、训练神经网络
python
def train_neural_network(nn, X, y, learning_rate=0.1, num_epochs=1000, print_every=100):
"""
训练神经网络
参数:
nn: 神经网络实例
X: 训练数据 (m, n_features)
y: 训练标签 (m,)
learning_rate: 学习率
num_epochs: 训练轮数
print_every: 打印频率
返回:
loss_history: 损失历史
"""
# 数据预处理
X = X.T # 转置为 (n_features, m)
y = y.reshape(1, -1) # 转置为 (1, m)
loss_history = []
for epoch in range(num_epochs):
# 前向传播
A2, cache = nn.forward(X)
# 计算损失
loss = nn.compute_loss(A2, y)
loss_history.append(loss)
# 反向传播
grads = nn.backward(A2, y, cache)
# 更新参数
nn.update_parameters(grads, learning_rate)
# 打印训练信息
if (epoch + 1) % print_every == 0:
predictions = nn.predict(X)
accuracy = np.mean(predictions == y)
print(f"Epoch {epoch+1}: loss = {loss:.4f}, accuracy = {accuracy:.4f}")
return loss_history
# 训练网络
print("开始训练神经网络...")
loss_history = train_neural_network(nn, X, y, learning_rate=0.5, num_epochs=2000, print_every=200)
print("训练完成!")
# 最终评估
X_eval = X.T # (n_features, m)
y_eval = y.reshape(-1)
predictions = nn.predict(X_eval).flatten()
accuracy = np.mean(predictions == y_eval)
print(f"最终准确率: {accuracy:.4f}")
print(f"最终损失: {loss_history[-1]:.4f}")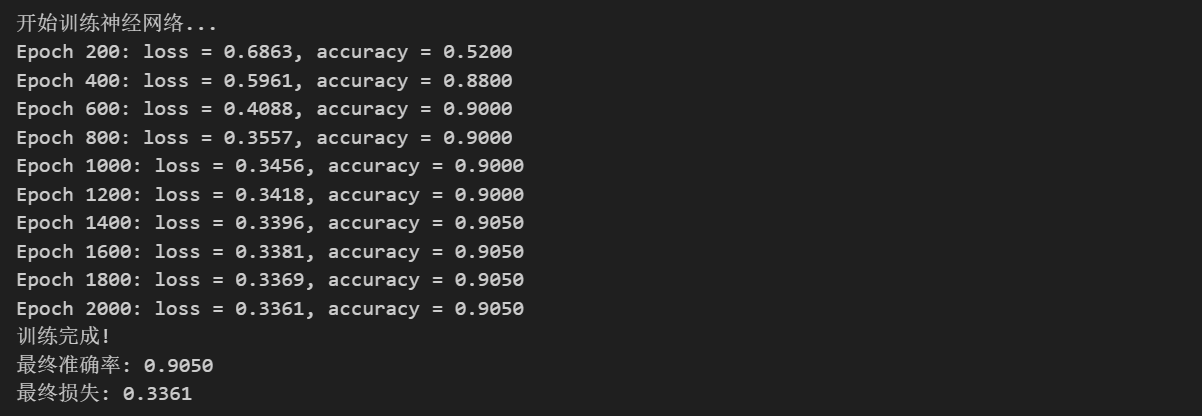
5、可视化训练过程
python
# 可视化损失收敛
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(loss_history, 'b-', linewidth=2)
plt.xlabel('训练轮数')
plt.ylabel('损失值')
plt.title('损失函数收敛过程')
plt.grid(True, alpha=0.3)
plt.yscale('log')
plt.subplot(1, 2, 2)
plt.plot(loss_history[:500], 'r-', linewidth=2)
plt.xlabel('训练轮数')
plt.ylabel('损失值')
plt.title('损失函数收敛过程 (前500轮)')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print(f"初始损失: {loss_history[0]:.4f}")
print(f"最终损失: {loss_history[-1]:.4f}")
print(f"损失减少: {loss_history[0] - loss_history[-1]:.4f}")
# 可视化决策边界
def plot_decision_boundary(nn, X, y):
# 创建网格
x_min, x_max = X[:, 0].min() - 0.1, X[:, 0].max() + 0.1
y_min, y_max = X[:, 1].min() - 0.1, X[:, 1].max() + 0.1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
np.linspace(y_min, y_max, 100))
# 预测网格点
grid_points = np.c_[xx.ravel(), yy.ravel()].T
Z = nn.predict(grid_points).reshape(xx.shape)
# 绘制
plt.contourf(xx, yy, Z, alpha=0.3, cmap='RdYlBu')
plt.scatter(X[y==1, 0], X[y==1, 1], c='red', alpha=0.7, label='苹果', s=50, edgecolors='k')
plt.scatter(X[y==0, 0], X[y==0, 1], c='orange', alpha=0.7, label='橙子', s=50, edgecolors='k')
plt.xlabel('重量 (kg)')
plt.ylabel('颜色值 (0-1)')
plt.title('神经网络决策边界')
plt.legend()
plt.grid(True, alpha=0.3)
plt.figure(figsize=(10, 6))
plot_decision_boundary(nn, X, y)
plt.show()
# 分析预测结果
from sklearn.metrics import classification_report, confusion_matrix
print("分类报告:")
print(classification_report(y_eval, predictions, target_names=['橙子', '苹果']))
print("混淆矩阵:")
cm = confusion_matrix(y_eval, predictions)
print(cm)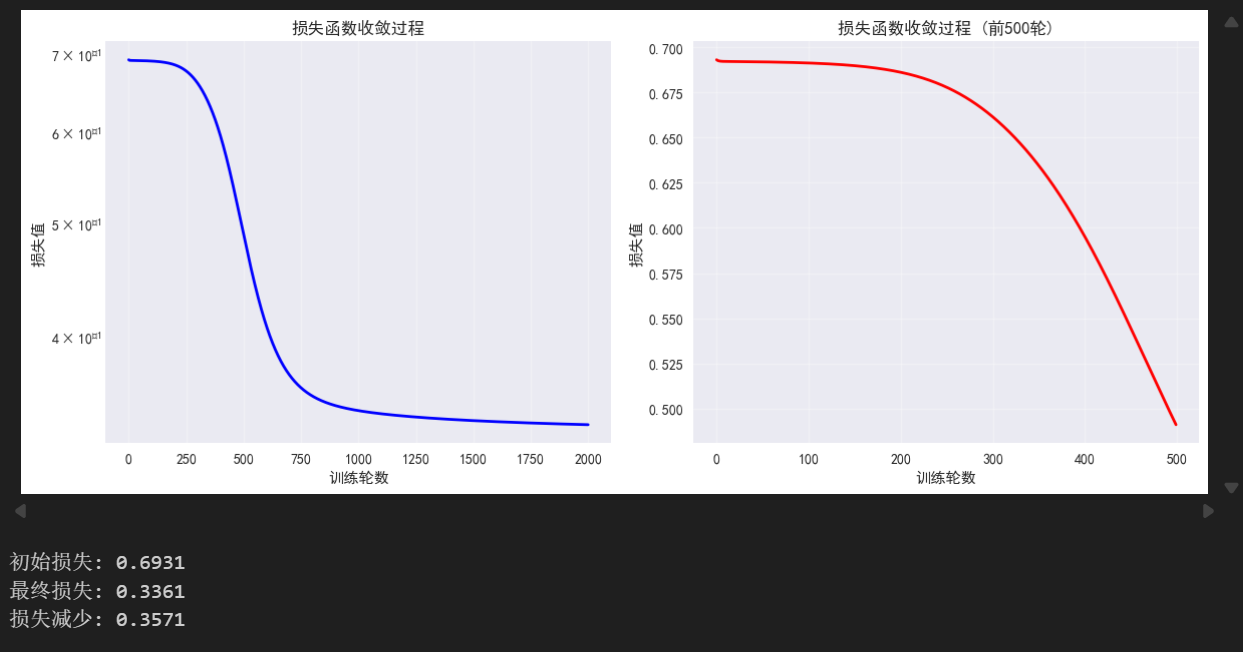
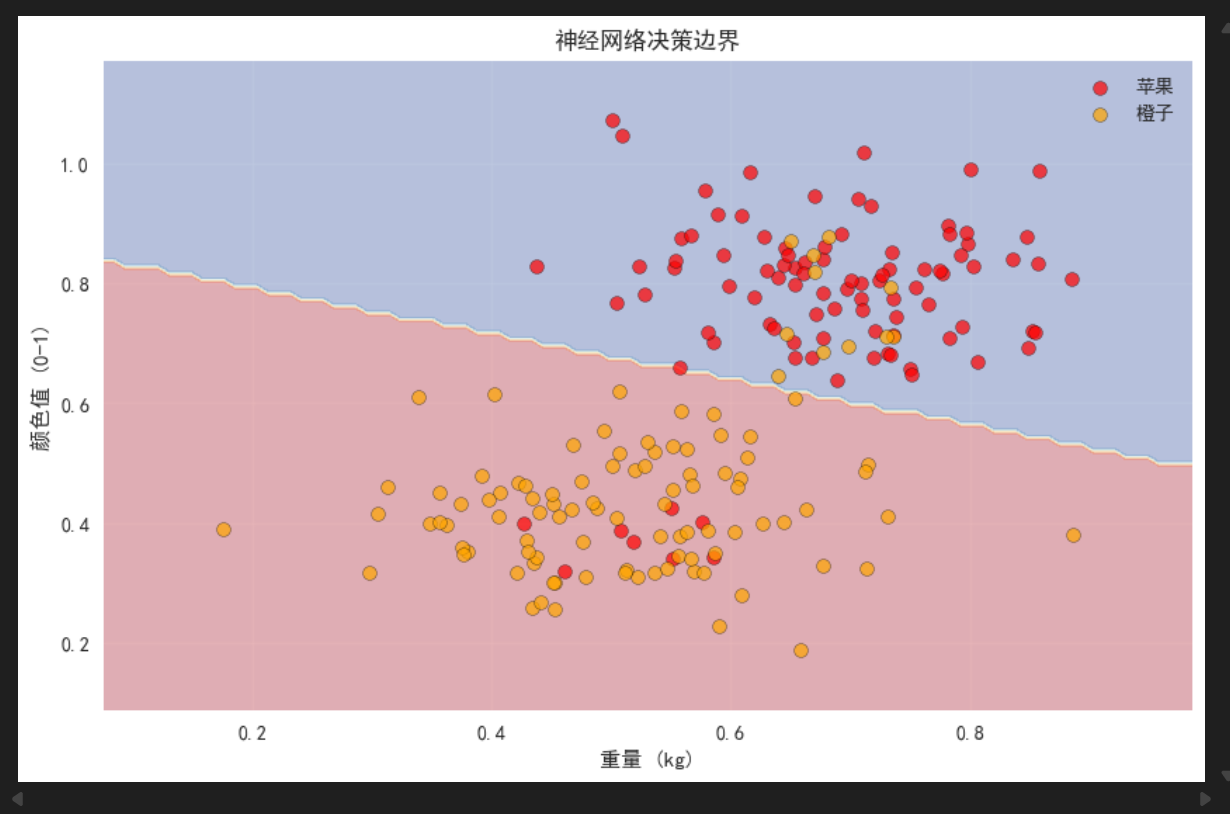
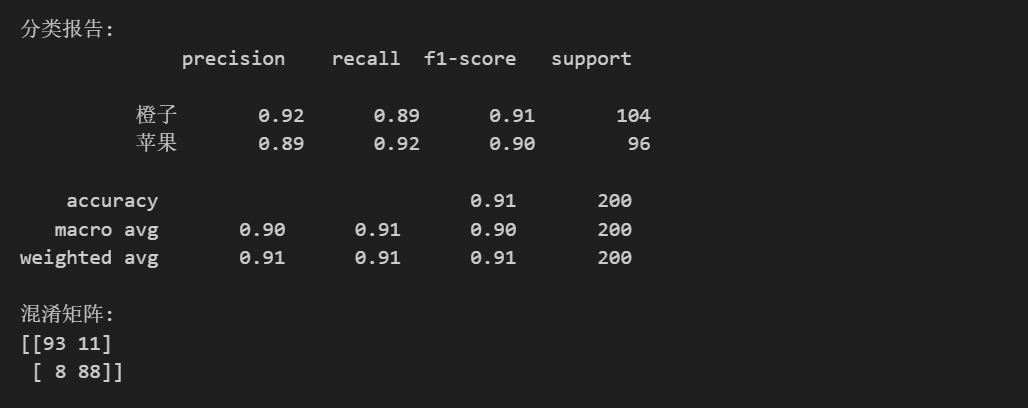
可以看到,整体来说分类的结果准确率达到了90%左右,还是比较成功的。相比起之前介绍的线性回归,神经网络可以更好的对数据进行拟合,能处理非线性的问题,目前来说,神经网络或者是深度学习已经是一个非常成功的技术,深刻地影响着各行各业。
通过这两篇文章,补充了反向传播的知识,完成了从理论到数值的落地实践下一篇文章,我们会开始尝试用封装好的函数来完成一个简单的深度学习项目,并继续介绍相关原理