GPTQ原理浅析及简单实现

GPTQ原理浅析及简单实现

GPTQ论文地址：GPTQ arxiv

优化目标

GPTQ作为逐层逐权重矩阵量化算法，每次运行只考虑一个权重矩阵 W ∈ R m × d W \in \mathbb{R}^{m \times d} W∈Rm×d。给定固定的校准集输入 X ∈ R d × n X \in \mathbb{R}^{d \times n} X∈Rd×n， W ^ \hat{W} W^作为 W W W量化-反量化后的矩阵，优化下面的目标函数：

E ( W ^ ) = ∣ ∣ W X − W ^ X ∣ ∣ 2 2 \text{E}(\hat{W}) = ||WX - \hat{W}X||_2^2 E(W^)=∣∣WX−W^X∣∣22

最终目标是找到一个 W ^ \hat{W} W^，让 E ( W ^ ) \text{E}(\hat{W}) E(W^)最小，即：

arg min ⁡ W ^ ∣ ∣ W X − W ^ X ∣ ∣ 2 2 \argmin_{\hat{W}} ||WX - \hat{W}X||_2^2 W^argmin∣∣WX−W^X∣∣22

对于上式目标函数我们发现， W W W中量化每一行 w ∈ R d w \in \mathbb{R}^d w∈Rd对 E ( W ^ ) \text{E}(\hat{W}) E(W^)的影响都是独立不相关的，因此可以单独考虑量化每一行 w T w^T wT，此时目标函数变成：

E ( w ^ ) = ∣ ∣ w T X − w ^ T X ∣ ∣ 2 2 \text{E}(\hat{w}) = ||w^TX - \hat{w}^TX||_2^2 E(w^)=∣∣wTX−w^TX∣∣22

泰勒展开

GPTQ算法原理的第一步是将目标函数 E ( w ^ ) \text{E}(\hat{w}) E(w^)，进行泰勒展开，为了计算方便我们不对 w ^ \hat{w} w^作为函数自变量，而是将量化误差 Δ w = w ^ − w \Delta w = \hat{w} - w Δw=w^−w作为函数自变量，对其进行泰勒展开。

E ( w ^ ) = ∣ ∣ w T X − w ^ T X ∣ ∣ 2 2 = ∣ ∣ − Δ w T X ∣ ∣ 2 2 = ∣ ∣ Δ w T X ∣ ∣ 2 2 \text{E}(\hat{w}) = ||w^TX - \hat{w}^TX||_2^2 = ||-\Delta w^T X||_2^2 = ||\Delta w^T X||_2^2 E(w^)=∣∣wTX−w^TX∣∣22=∣∣−ΔwTX∣∣22=∣∣ΔwTX∣∣22

则 E ( w ^ ) \text{E}(\hat{w}) E(w^)现在是关于 Δ w \Delta w Δw的函数：

E ( Δ w ) = ∣ ∣ Δ w T X ∣ ∣ 2 2 \text{E}(\Delta w) = ||\Delta w^T X||_2^2 E(Δw)=∣∣ΔwTX∣∣22

考虑在 Δ w = 0 \Delta w = 0 Δw=0处进行泰勒展开：

E ( Δ w ) = E ( 0 ) + ∇ E ( 0 ) T Δ w + 1 2 Δ w T H Δ w + O ( ∣ ∣ Δ w ∣ ∣ 3 ) \text{E}(\Delta w) = \text{E}(0) + \nabla \text{E}(0)^T\Delta w + \frac{1}{2}\Delta w^TH\Delta w+O(||\Delta w||^3) E(Δw)=E(0)+∇E(0)TΔw+21ΔwTHΔw+O(∣∣Δw∣∣3)

其中，显然 E ( 0 ) = 0 \text{E}(0)=0 E(0)=0，然后考虑一阶项 ∇ E ( 0 ) \nabla \text{E}(0) ∇E(0)，现在证明 ∇ E ( 0 ) = 0 \nabla \text{E}(0) = 0 ∇E(0)=0。先对目标函数 E \text{E} E做二次型：

E = ∣ ∣ Δ w T X ∣ ∣ 2 2 = ( Δ w T X ) ( X T Δ w ) = Δ w T ( X X T ) Δ w \text{E} = ||\Delta w^T X||_2^2 = (\Delta w^TX)(X^T\Delta w) = \Delta w^T(XX^T)\Delta w E=∣∣ΔwTX∣∣22=(ΔwTX)(XTΔw)=ΔwT(XXT)Δw

对 E \text{E} E求导，可得：

∇ E ( Δ w ) = 2 X X T Δ w \nabla \text{E}(\Delta w) = 2XX^T\Delta w ∇E(Δw)=2XXTΔw

显然 ∇ E ( 0 ) = 0 \nabla \text{E}(0) = 0 ∇E(0)=0。

忽略高阶展开项，则现在目标函数变为：

E ( Δ w ) = 1 2 Δ w T H Δ w \text{E}(\Delta w) = \frac{1}{2}\Delta w^TH\Delta w E(Δw)=21ΔwTHΔw

其中 H H H称为Hessian矩阵，为 E \text{E} E的二阶导数在 Δ w = 0 \Delta w=0 Δw=0处的函数值矩阵。

现在证明 H = 2 X X T H=2XX^T H=2XXT，对 ∇ E \nabla \text{E} ∇E再次求导：

H = ∇ 2 E = 2 X X T H = \nabla^2 \text{E} = 2XX^T H=∇2E=2XXT

这就是论文给出的第一个结论 H = 2 X X T H = 2XX^T H=2XXT，与目前量化的行 w w w无关，所以所有行都共用一个 H H H矩阵。

寻找目标量化权重

GPTQ第二步是基于一种迭代搜索的算法，每次在当前行 w w w中，寻找一个最佳候选权重 w p w_p wp，将 w p w_p wp量化，其他权重不量化，此时产生的 Δ w \Delta w Δw应该让 E ( Δ w ) \text{E}(\Delta w) E(Δw)最小，将挑选 w p w_p wp的操作表达为一个约束方程：

e q T Δ w + w q = quant-dequant ( w q ) e_q^T \Delta w + w_q = \text{quant-dequant}(w_q) eqTΔw+wq=quant-dequant(wq)

其中 e q T e_q^T eqT表示向量 [ 0 , 0 , ... , 1 p , ... , 0 ] [0,0,\dots,1_p,\dots,0] [0,0,...,1p,...,0]在 p p p位置上的One-Hot向量， e q T Δ w e_q^T \Delta w eqTΔw表示从 Δ w \Delta w Δw中选出 Δ w p \Delta w_p Δwp， quant-dequant ( w q ) \text{quant-dequant}(w_q) quant-dequant(wq)表示将 w q w_q wq量化再反量化。

目标函数为 E ( Δ w ) = 1 2 Δ w T H Δ w \text{E}(\Delta w) = \frac{1}{2}\Delta w^TH\Delta w E(Δw)=21ΔwTHΔw，这是一个带约束函数的多元函数优化问题，使用拉格朗日乘数法来解决该最优化问题：

L ( Δ w , λ ) = 1 2 Δ w T H Δ w + λ ( e q T Δ w + w q − quant-dequant ( w q ) ) L(\Delta w, \lambda) = \frac{1}{2}\Delta w^TH\Delta w + \lambda(e_q^T \Delta w + w_q - \text{quant-dequant}(w_q)) L(Δw,λ)=21ΔwTHΔw+λ(eqTΔw+wq−quant-dequant(wq))

求导解方程可以得到GPTQ的核心公式：

Δ w = − w q − quant-dequant ( w q ) H q q − 1 H : , q − 1 \Delta w = - \frac{w_q - \text{quant-dequant}(w_q)}{H^{-1}{qq}} H^{-1}{:,q} Δw=−Hqq−1wq−quant-dequant(wq)H:,q−1

w q = arg min ⁡ w q = ( quant-dequant ( w q ) − w q ) 2 H q q − 1 w_q = \argmin_{w_q} = \frac{(\text{quant-dequant}(w_q) - w_q)^2}{H^{-1}_{qq}} wq=wqargmin=Hqq−1(quant-dequant(wq)−wq)2

其中公式二 w q w_q wq告诉了我们应该选哪个 w q w_q wq进行量化，公式一告诉我们如果选择了 w q w_q wq进行量化，如何通过补偿 Δ w \Delta w Δw到其他权重才能使得 E \text{E} E最小。

那么整个迭代过程可以总结为，令目前未量化的权重集合为 w w w：

1. 通过公式1在 w w w中选出最佳 w q w_q wq。
2. 量化 w q w_q wq。
3. 通过公式2计算补偿 Δ w \Delta w Δw，并加到权重集合 w w w中的对应权重上。
4. 在 w w w中移除 w q w_q wq。
5. 用当前 w w w，更新 H H H矩阵。
6. 重复步骤1，直到所有权重量化完成。

更新 H H H矩阵

Arbitrary Order Insight

整个GPTQ的核心优化全部都是围绕如何更新 H H H矩阵展开的，按照最朴素的方法来说，每次移除一个 w q w_q wq，需要在 H H H矩阵中删除对应的 p p p行和 p p p列，然后再次求 H H H的逆矩阵 H − 1 H^{-1} H−1，其中产生了巨大的计算压力，不利于当今超大权重矩阵的计算，如下图所示：

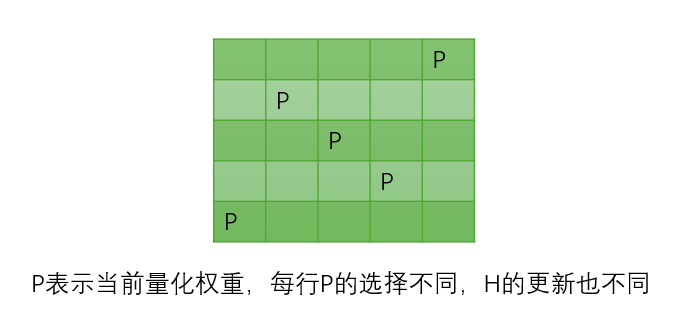
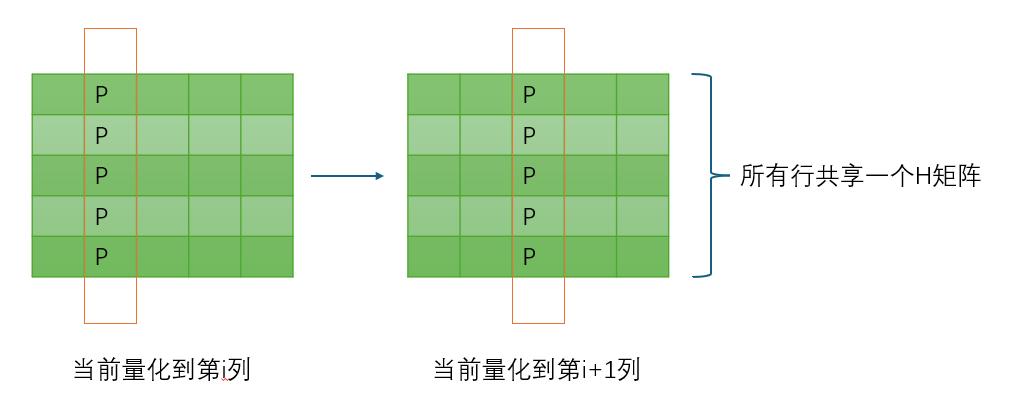
GPTQ发现，如果 W W W中每行 w w w挑选 w q w_q wq的顺序不是一样的，那么每行都必须单独维护自己的 H H H矩阵，如果 W W W有 m m m行，需要单独维护 m m m个 H H H矩阵，这对IO和计算不利。但是GPTQ发现如果每行都按一样的顺序选择 w q w_q wq，那么只需要共用一个 H H H矩阵就可以了，这大大减少了计算压力，并且和原始贪心选择相比，不会对量化精度产生太大影响。所以，在GPTQ中，所有行的量化可以同步进行，每行从左到右依次量化。这是论文中的观察1：Arbitrary Order Insight，如下图所示：

Lazy Batch-Updates

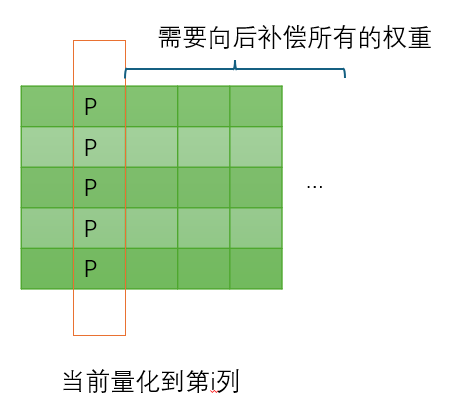
GPTQ发现每次量化完一行，向后补偿 Δ w \Delta w Δw的时候需要计算全部的补偿参数并加上去，如果 W W W特别大，那么每次迭代几乎就需要更新整个矩阵，整个过程时间都花在IO来回搬运矩阵上了，计算时间占比很低，如图所示：

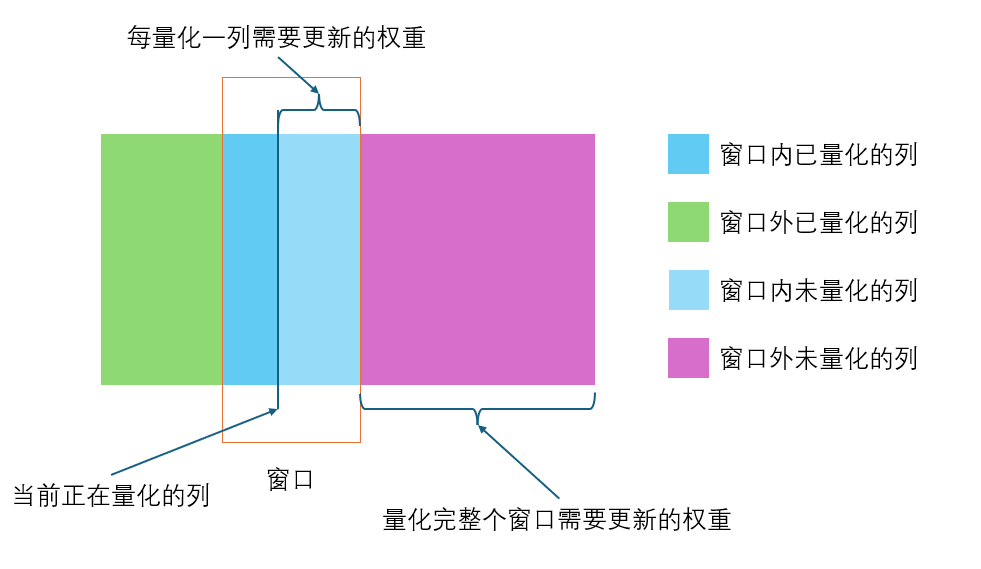
GPTQ给出的解决方案是维护一个窗口，每次量化完一列，只更新窗口内的剩余权重，并把这次的 w q − quant-dequant ( w q ) w_q - \text{quant-dequant}(w_q) wq−quant-dequant(wq)先记录在另外一个误差矩阵 E E E中，等到窗口内的权重全部量化完成，通过矩阵 E E E一次性更新窗口外的权重，最后将窗口移动到下一个窗口位置，这样做假设窗口大小为128，那么只需要每更新128列才更新一次全部的矩阵，虽然不会降低计算量，但是降低了IO时间的比例，如图所示：

上述优化对应论文观察2：Lazy Batch-Updates。

Cholesky Reformulation

GPTQ给出的最后一个观察是最为关键的，也是最为巧妙的。前两个优化每次都需要更新 H − 1 H^{-1} H−1，第三个优化可以不用更新 H − 1 H^{-1} H−1。

Cholesky分解是将对称正定矩阵分解为下三角矩阵与其转置乘积的矩阵分解方法，将 H − 1 = ( 2 X X T + λ I ) − 1 H^{-1}=(2XX^T+\lambda I)^{-1} H−1=(2XXT+λI)−1进行Cholesky分解：

H − 1 = R R T H^{-1} = R R^T H−1=RRT

其中 λ I \lambda I λI为了增加数值稳定性，否则当 X X X的秩不够， H H H是一个奇异矩阵，会造成无法计算。

在GPTQ的论文中：

H − 1 ← Cholesky ( H − 1 ) T H^{-1} \leftarrow \text{Cholesky}(H^{-1})^T H−1←Cholesky(H−1)T

表示将 H − 1 H^{-1} H−1进行Cholesky分解，得到矩阵 R T R^T RT，赋值给 H − 1 H^{-1} H−1，此时 H − 1 H^{-1} H−1就是上三角矩阵 R T R^T RT，用Python表示就是：

H = 2 * X @ X.T + + 0.01 * np.eye(n)
H_I = np.linalg.inv(H)
H_I = np.linalg.cholesky(H_I).T

Cholesky分解之后，我们有一个非常重要的性质：我们去掉 H H H的第一行第一列，相当于去掉 R R R的第一行第一列，用Python表示为：

H = 2 * X @ X.T + 0.01 * np.eye(n)
H_I = np.linalg.inv(H)
R_T = np.linalg.cholesky(H_I).T

assert np.allclose(np.linalg.inv(H[1:,1:]), R_T[1:,1:].T @ R_T[1:,1:])

这给了我们一些优化思路，因为我们是从左到右按顺序量化每行，那么每次就是相当于去掉 H H H的第一行第一列，那么我们只需要维护 R R R通过一个矩阵乘法就能还原出更新后的 H − 1 H^{-1} H−1。并且，每次去掉第一行第一列， R R R永远是一个下三角矩阵。

但是我们并不真的需要每次都通过 R R T RR^T RRT恢复 H − 1 H^{-1} H−1。

这是因为，回到补偿更新公式：

Δ w = − w q − quant-dequant ( w q ) H q q − 1 H : , q − 1 \Delta w = - \frac{w_q - \text{quant-dequant}(w_q)}{H^{-1}{qq}} H^{-1}{:,q} Δw=−Hqq−1wq−quant-dequant(wq)H:,q−1

我们发现每次我们需要的不是全部的 H − 1 H^{-1} H−1，我们只需要 H − 1 H^{-1} H−1的第 q q q个对角元素 H q q − 1 H^{-1}{qq} Hqq−1和第 q q q列 H : , q − 1 H^{-1}{:,q} H:,q−1。

为了方便，假设我们每次需要的是第一个对角元素 H 11 − 1 H^{-1}_{11} H11−1：

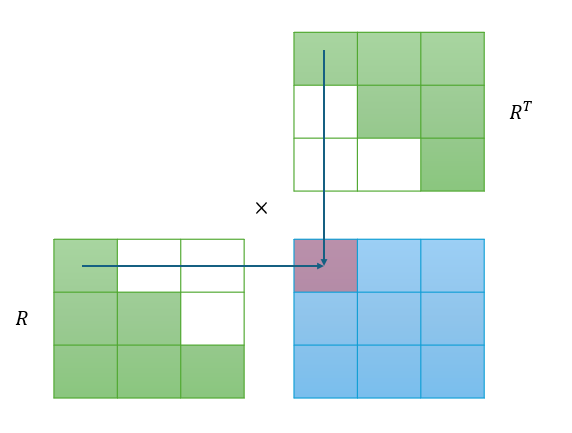
根据上图可知，白色方块表示0：

H 11 − 1 = ( R 11 T ) 2 H^{-1}{11} = (R^T{11})^2 H11−1=(R11T)2

同理计算第1列：

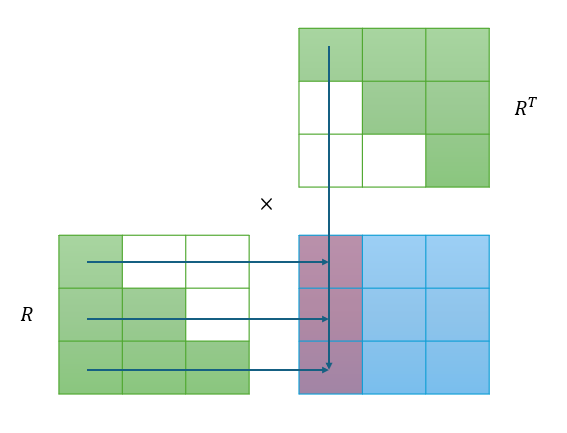
H : , 1 − 1 = R : , 1 ⋅ R 11 = ( R 1 , : T ⋅ R 11 T ) T H^{-1}{:,1} = R{:,1} \cdot R_{11} = (R^T_{1,:} \cdot R^T_{11})^T H:,1−1=R:,1⋅R11=(R1,:T⋅R11T)T

因此，我们完全不需要还原 H − 1 H^{-1} H−1，就能把我们想要的元素拿出来。

最后补偿计算就是：

Δ w = − w 1 − quant-dequant ( w 1 ) ( R 11 T ) 2 ( R 1 , : T ⋅ R 11 T ) T = w 1 − quant-dequant ( w 1 ) R 11 T ( R 1 , : T ) T \Delta w = - \frac{w_1 - \text{quant-dequant}(w_1)}{(R^T_{11})^2} (R^T_{1,:} \cdot R^T_{11})^T = \frac{w_1 - \text{quant-dequant}(w_1)}{R^T_{11}} (R^T_{1,:})^T Δw=−(R11T)2w1−quant-dequant(w1)(R1,:T⋅R11T)T=R11Tw1−quant-dequant(w1)(R1,:T)T

GPTQ算法

通过上面的分析，我们就可以阅读GPTQ论文中给出的算法流程：

首先在做算法之前，通过校准集合 X X X预计算 H − 1 H^{-1} H−1。

第一行 Q Q Q矩阵用于保存 W W W量化反量化的结果，第二行的 E E E用于保存一个窗口 B B B内的量化误差 w q − quant-dequant ( w q ) w_q - \text{quant-dequant}(w_q) wq−quant-dequant(wq)，以便于等到我们量化完一个窗口，更新补偿所有权重。

第三行Cholesky分解 H − 1 H^{-1} H−1，注意下面的 H − 1 H^{-1} H−1都指的是 H − 1 = R R T H^{-1}=RR^T H−1=RRT中的 R T R^T RT。

第四行的for表示窗口间迭代，第五行的for表示窗口内迭代，每次同步量化一个列 j j j。

第六行将 W W W的第 j j j列量化反量化，结果保存到 Q Q Q中。

第七行计算第 j j j列的量化误差，注意我们这里除掉了一个对角元素 R j j T R^T_{jj} RjjT，表示上述补偿方程中的：

w j − quant-dequant ( w j ) R j j T \frac{w_j - \text{quant-dequant}(w_j)}{R^T_{jj}} RjjTwj−quant-dequant(wj)

第八行补偿更新窗口内剩余权重，从第 j j j行到 i + B i+B i+B行，原来我们是需要 R j , : T R^T_{j,:} Rj,:T，但是我们只更新窗口内的行，也就是取 R j , j : i + B T R^T_{j,j:i+B} Rj,j:i+BT就可以了。

每次量化完第 j j j列，理论应该去掉当前 R T R^T RT的第一行第一列，但是我们实际算法并不需要特意在内存中去掉。

最后每次量化完一个窗口，更新补偿窗口外的所有权重，方法同理补偿更新窗口内剩余权重。

Python 简单实现

import numpy as np

# Quant Func
def quant(arr, zero, scale, bits):
    return np.clip(np.round((arr - zero) / scale * (2**bits - 1)), 0, 2**bits - 1)

def dequant(arr, zero, scale, bits):
    return arr / (2**bits - 1) * scale + zero

# Params
m = 1024
n = 1024
d = 1024
window_size = 128
bits = 4

W = np.random.rand(m, d)
W_ref = W.copy()
X = np.random.rand(d, n)

H = 2 * X @ X.T
H_I = np.linalg.inv(H + 0.001 * np.eye(d))
# Cholesky
H_I = np.linalg.cholesky(H_I).T

num_window = (d + window_size - 1) // window_size

zero = np.min(W)
scale = np.max(W - zero)

Q = np.zeros_like(W)
E = np.zeros((m, window_size))

# GPTQ
for window_idx in range(0, num_window):
    window_start = window_idx * window_size
    window_end = min(d, (window_idx + 1) * window_size)
    for i in range(window_start, window_end):
        Q[:,i] = quant(W[:,i], zero, scale, bits)
        E[:,i - window_start] = (W[:,i] - dequant(Q[:,i], zero, scale, bits)) / H_I[i,i]
        W[:,i:window_end] = W[:,i:window_end] - E[:,[i - window_start]] @ H_I[[i],i:window_end]
    W[:,window_end:] = W[:,window_end:] - E @ H_I[window_start:window_end,window_end:]

# Error
err = W_ref @ X - W @ X
err_ref = W_ref @ X - dequant(quant(W_ref, zero, scale, bits), zero, scale, bits) @ X
# GPTQ:186.92, BASELINE:99670.94
print(f"GPTQ:{np.linalg.norm(err, ord=2)**2}, BASELINE:{np.linalg.norm(err_ref, ord=2)**2}", )

通过输出，GPTQ的误差函数值远小于朴素量化的误差函数值。