文章目录
- 前言
- [5.2.1 基本形式的虚功原理](#5.2.1 基本形式的虚功原理)
- [5.2.2 广义坐标下的虚功原理](#5.2.2 广义坐标下的虚功原理)
-
- [例 单个自由质点,求平衡位形](#例 单个自由质点,求平衡位形)
- [5.2.4 保守系统下的虚功原理](#5.2.4 保守系统下的虚功原理)
- 参考资料
前言
本文是分析力学学习笔记,主要参考为 哈工大任延宇老师的《理论力学(物理类)》教程 分析力学部分,感谢任老师贡献如此精美的课程。为方便大家对比学习,本文章节按照原教程排版。
5.2.1 基本形式的虚功原理
对于稳定约束,也叫定常约束 ( ∂ f / ∂ t = 0 \partial f / \partial t = 0 ∂f/∂t=0), 也就是说, 在时不变 (等时) 的情况下, 变分算符 δ \delta δ 和微分算符 d \mathrm{d} d 是等价的, 因此, 可以将虚位移 δ r ⃗ i \delta \vec{r}_i δr i 看做是实位移 d r ⃗ i \mathrm{d} \vec{r}_i dr i 的特例。
对于非稳定约束,也叫非定常约束 , 实位移和虚位移是不同的。
非定常约束是指约束会随着时间的变化而变化。比如说手掌上的激光笔只受定常约束(手掌固定)时,可以前后左右移动;当受非定常约束(手掌上下移动)时,则可以上下前后左右移动。
模仿牛顿力学的功的定义, 有虚功 (virtual work)
δ W = ∑ i = 1 ( F ⃗ i + R ⃗ i ) ⋅ δ r ⃗ i , \delta W = \sum_{i=1} (\vec{F}_i + \vec{R}_i) \cdot \delta \vec{r}_i, δW=i=1∑(F i+R i)⋅δr i,
其中 F ⃗ i \vec{F}_i F i 是主动力, R ⃗ i \vec{R}i R i 是约束力。满足
∑ i = 1 R ⃗ i ⋅ δ r ⃗ i = 0 \sum{i=1} \vec{R}_i \cdot \delta \vec{r}_i = 0 i=1∑R i⋅δr i=0
的约束称为理想约束, 即约束力对虚位移所做的功为零 。
进而, 满足理想约束下的虚功为
δ W = ∑ i = 1 F ⃗ i ⋅ δ r ⃗ i . \delta W = \sum_{i=1} \vec{F}_i \cdot \delta \vec{r}_i. δW=i=1∑F i⋅δr i.
令 δ W = 0 \delta W = 0 δW=0, 即得到虚功原理
δ W = ∑ i = 1 F ⃗ i ⋅ δ r ⃗ i = 0. \delta W = \sum_{i=1} \vec{F}_i \cdot \delta \vec{r}_i = 0. δW=i=1∑F i⋅δr i=0.
虚功原理
若 { r ⃗ i } \{\vec{r}_i\} {r i} 是约束允许的平衡位形 ( ∂ f / ∂ t = 0 \partial f / \partial t = 0 ∂f/∂t=0)
则 系统在该位形下维持平衡的充要条件是: ∑ i = 1 n F ⃗ i ⋅ δ r ⃗ i = 0 \displaystyle \sum_{i=1}^{n} \vec{F}_i \cdot \delta \vec{r}_i = 0 i=1∑nF i⋅δr i=0
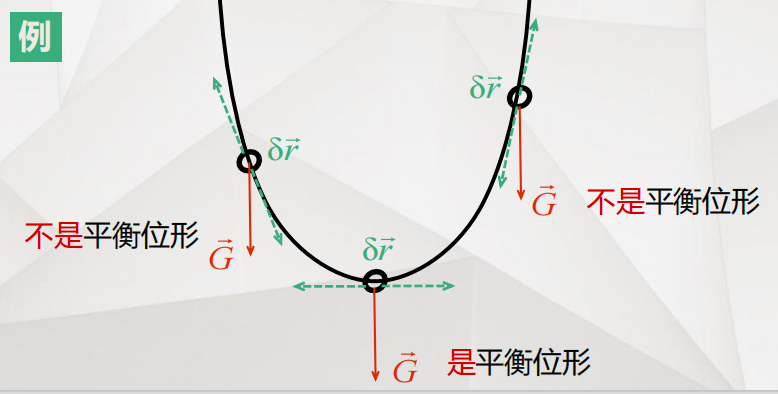
"证明" 牛顿力学给出的平衡条件:
必要性 ∀ i , F ⃗ i + R ⃗ i = 0 ⇒ ∑ i ( F ⃗ i + R ⃗ i ) ⋅ δ r ⃗ i = 0 \forall i, \quad \vec{F}_i + \vec{R}i = 0 \Rightarrow \sum{i} (\vec{F}_i + \vec{R}_i) \cdot \delta \vec{r}_i = 0 ∀i,F i+R i=0⇒∑i(F i+R i)⋅δr i=0
理想系统: ⇒ ∑ i F ⃗ i ⋅ δ r ⃗ i = 0 \Rightarrow \sum_{i} \vec{F}_i \cdot \delta \vec{r}_i = 0 ⇒∑iF i⋅δr i=0
充分性 ∑ i ( F ⃗ i + R ⃗ i ) ⋅ δ r ⃗ i = 0 \displaystyle \sum_{i} (\vec{F}_i + \vec{R}_i) \cdot \delta \vec{r}_i = 0 i∑(F i+R i)⋅δr i=0
实位移是虚位移的一个: ∑ i ( F ⃗ i + R ⃗ i ) ⋅ d r ⃗ i = 0 d T = 0 \displaystyle \sum_{i} (\vec{F}_i + \vec{R}_i) \cdot \mathrm{d}\vec{r}_i = 0 \quad \mathrm{d}T = 0 i∑(F i+R i)⋅dr i=0dT=0
5.2.2 广义坐标下的虚功原理
例 单个自由质点,求平衡位形
牛顿力学
F x = F y = F z = 0 F_x = F_y = F_z = 0 Fx=Fy=Fz=0
分析力学
F x δ x + F y δ y + F z δ z = 0 F_x \delta x + F_y \delta y + F_z \delta z = 0 Fxδx+Fyδy+Fzδz=0
由于 δ x \delta x δx、 δ y \delta y δy、 δ z \delta z δz 独立,因此
F x = F y = F z = 0 F_x = F_y = F_z = 0 Fx=Fy=Fz=0
三个虚位移分量各自独立,方向不同,线性无关,所以前面系数必须都为 0 。
r ⃗ i = r ⃗ i ( q 1 , q 2 , ... , q s , t ) d r ⃗ i = ∂ r ⃗ i ∂ t d t + ∑ α = 1 s ∂ r ⃗ i ∂ q α d q α ⇒ δ r ⃗ i = ∂ r ⃗ i ∂ t δ t + ∑ α = 1 s ∂ r ⃗ i ∂ q α δ q α \begin{aligned} \vec{r}_i &= \vec{r}_i(q_1, q_2, \dots, q_s, t) \\ d\vec{r}i &= \frac{\partial \vec{r}i}{\partial t} dt + \sum{\alpha=1}^{s} \frac{\partial \vec{r}i}{\partial q\alpha} dq\alpha \\ \Rightarrow \delta \vec{r}i &= \frac{\partial \vec{r}i}{\partial t} \delta t + \sum{\alpha=1}^{s} \frac{\partial \vec{r}i}{\partial q\alpha} \delta q\alpha \end{aligned} r idr i⇒δr i=r i(q1,q2,...,qs,t)=∂t∂r idt+α=1∑s∂qα∂r idqα=∂t∂r iδt+α=1∑s∂qα∂r iδqα
由于这里是等时变分, δ t = 0 \delta t = 0 δt=0,那么有
δ r ⃗ i = ∑ α = 1 s ∂ r ⃗ i ∂ q α δ q α \delta \vec{r}i = \sum{\alpha=1}^{s} \frac{\partial \vec{r}i}{\partial q\alpha} \delta q_\alpha δr i=α=1∑s∂qα∂r iδqα
代入 ∑ i = 1 F ⃗ i ⋅ δ r ⃗ i = 0 \sum_{i=1} \vec{F}_i \cdot \delta \vec{r}_i = 0 i=1∑F i⋅δr i=0
⇒ ∑ i F ⃗ i ⋅ ( ∑ α = 1 s ∂ r ⃗ i ∂ q α δ q α ) = 0 ⇒ ∑ α = 1 s ( ∑ i F ⃗ i ⋅ ∂ r ⃗ i ∂ q α ) δ q α = 0 ⇒ ∑ i F ⃗ i ⋅ ∂ r ⃗ i ∂ q α = 0 \begin{aligned} \Rightarrow \sum_{i} \vec{F}i \cdot \left( \sum{\alpha=1}^{s} \frac{\partial \vec{r}i}{\partial q\alpha} \delta q_\alpha \right) &= 0 \\ \Rightarrow \sum_{\alpha=1}^{s} \left( \sum_{i} \vec{F}i \cdot \frac{\partial \vec{r}i}{\partial q\alpha} \right) \delta q\alpha &= 0 \\ \Rightarrow \sum_{i} \vec{F}_i \cdot \frac{\partial \vec{r}i}{\partial q\alpha} &= 0 \end{aligned} ⇒i∑F i⋅(α=1∑s∂qα∂r iδqα)⇒α=1∑s(i∑F i⋅∂qα∂r i)δqα⇒i∑F i⋅∂qα∂r i=0=0=0
由于 δ q α \delta q_\alpha δqα线性无关,所以前面系数为 0。
对于这个公式,被称之为广义力,记为 Q α Q_\alpha Qα,即
Q α = ∑ i = 1 n F ⃗ i ⋅ ∂ r ⃗ i ∂ q α = 0 Q_\alpha = \sum_{i=1}^n \vec{F}_i \cdot \frac{\partial \vec{r}i}{\partial q\alpha}=0 Qα=i=1∑nF i⋅∂qα∂r i=0
5.2.4 保守系统下的虚功原理
在一个保守系统中,力 F ⃗ i \vec{F}i F i 可以表示为位能(势能) V V V 的负梯度:
F ⃗ i = − ∇ i V = − ( ∂ V ∂ x i i ⃗ + ∂ V ∂ y i j ⃗ + ∂ V ∂ z i k ⃗ ) \vec{F}i = -\nabla_i V = -\left( \frac{\partial V}{\partial x_i}\vec{i} + \frac{\partial V}{\partial y_i}\vec{j} + \frac{\partial V}{\partial z_i}\vec{k} \right) F i=−∇iV=−(∂xi∂Vi +∂yi∂Vj +∂zi∂Vk )
F ⃗ i = F x i i ⃗ + F y i j ⃗ + F z i k ⃗ = ( − ∂ V ∂ x i ) i ⃗ + ( − ∂ V ∂ y i ) j ⃗ + ( − ∂ V ∂ z i ) k ⃗ \vec{F}i = F{xi}\vec{i} + F{yi}\vec{j} + F{zi}\vec{k} = \left( -\frac{\partial V}{\partial x_i} \right)\vec{i} + \left( -\frac{\partial V}{\partial y_i} \right)\vec{j} + \left( -\frac{\partial V}{\partial z_i} \right)\vec{k} F i=Fxii +Fyij +Fzik =(−∂xi∂V)i +(−∂yi∂V)j +(−∂zi∂V)k
这代表力总是指向势能降低最快的方向。
∂ r ⃗ i ∂ q α = ∂ x i ∂ q α i ⃗ + ∂ y i ∂ q α j ⃗ + ∂ z i ∂ q α k ⃗ \frac{\partial \vec{r}i}{\partial q\alpha} = \frac{\partial x_i}{\partial q_\alpha}\vec{i} + \frac{\partial y_i}{\partial q_\alpha}\vec{j} + \frac{\partial z_i}{\partial q_\alpha}\vec{k} ∂qα∂r i=∂qα∂xii +∂qα∂yij +∂qα∂zik
Q α = ∑ i = 1 n − ( ∂ V ∂ x i ∂ x i ∂ q α + ∂ V ∂ y i ∂ y i ∂ q α + ∂ V ∂ z i ∂ z i ∂ q α ) = − ∂ V ∂ q α \begin{aligned} Q_\alpha &= \sum_{i=1}^{n} -\left( \frac{\partial V}{\partial x_i}\frac{\partial x_i}{\partial q_\alpha} + \frac{\partial V}{\partial y_i}\frac{\partial y_i}{\partial q_\alpha} + \frac{\partial V}{\partial z_i}\frac{\partial z_i}{\partial q_\alpha} \right) \\ & = - \frac{\partial V}{\partial q_\alpha} \end{aligned} Qα=i=1∑n−(∂xi∂V∂qα∂xi+∂yi∂V∂qα∂yi+∂zi∂V∂qα∂zi)=−∂qα∂V
那么,保守系统下的平衡条件: ∂ V ∂ q α = 0 \frac{\partial V}{\partial q_{\alpha}}=0 ∂qα∂V=0
参考资料
- 理论力学(物理类) 主讲:哈尔滨工业大学物理学院 任延宇 https://www.bilibili.com/video/BV1xJ411s78q
- 理论力学(物理类)(分析力学) https://www.bilibili.com/video/BV1hY411g7HG
- 分析力学 WANG LH https://gtbcamp.cn/notes/analytical-mechanics/analytical-mechanics.pdf
- 《经典力学》纸质书 高显