文章目录
前言
本文是分析力学学习笔记,主要参考为 哈工大任延宇老师的《理论力学(物理类)》教程 分析力学部分,感谢任老师贡献如此精美的课程。为方便大家对比学习,本文章节按照原教程排版。
5.1.1 分析力学引言
对于牛顿力学的出现,人们最大的感受就是震撼,然后尽快把它掌握用到各种实际问题。只要你足够努力,就可以顺理成章地成为一个优秀的建筑师,一个出色的科学家,一个了不起的发明家,等等等等。
你很难想象,去从事一项要另立一套新的力学体系的工作,这种想法实在是太疯狂了。因为在当时有没有一个新的力学体系,谁都不敢保证,或者即便是有可能,根本赶不上牛顿力学。况且,你我都清楚,创造一个新的力学体系,绝不是一件容易的事情,可能需要十几年,甚至几十年的时间。这么长的一个漫长的时间里,所承受的压力,阻力,其他人的非议,都是难以承受,难以想象。但是值得全人类庆幸和骄傲的是,还是有人毅然从事了这样一个疯狂的工作,并且最终取得了成功。
下边按照时间顺序罗列了其中一些重要成果。

- 1717 年,以约翰·伯努利为首提出了虚功原理,可以处理静力学问题。
- 1743 年,达朗伯给出了达朗伯原理,他建立了静力学和动力学这样一个密切的联系。
- 时隔一年,莫培督提出了他的最小作用量原理,为后来伟大的哈顿原理奠定了基础。
- 1760 年,拉格朗日提出了完全不同于牛顿力学的动力学方程拉格朗日方程,并于 1788 年出版了著名的《分析力学》,整本书没有一幅图,这在牛顿力学是绝对不可以想象的。
- 进入 19 世纪,1834、1835 年,哈顿发表两篇著名文章,分别奠定了今天的哈密顿原理和哈密顿正则方程。
- 1837 年,雅克比给出了处理哈密顿力学另外一套方案,就是所谓的哈密顿雅克比方法。
经过上述科学家努力,新的力学体系终于落成,而且它在很多方面体现得比牛顿力学更为优越,也更为高级。
- 首先,它的基本方程居然就是一个标量方程,这意味着在我们学习分析力学的时候,就可以摆脱选择坐标系、受力分析等等给你所带来的困扰
- 其次,在学习牛顿力学的时候儿,你要饱受约束力之苦,它是很难分析和计算的,因为它往往是未知的,而分析力学反而很巧妙的利用了约束力,这里边儿约束越多,反而方程的个数就越少。
- 此外,他给我们提供的降阶手段或者简化计算的方案也远远多于牛顿力学。
- 它最重要的一个特点,可能是当时发明分析力学的那些科学家们自己都没有想到,甚至在他们有生之年都没有预见到。这就是当人们提出量子力学之后,回过头再来看,发现它跟牛顿力学可以说是格格不入的,但是跟分析力学很多基本的公式却极为的相似。也就是说我们将要讲的分析力学很多重要的方程可以稍加修改,甚至不经修改,应用到量子力学仍然是最基本最重要的公式。因此我们说它是沟通经典物理到量子物理的桥梁,也是进入各个物理学前沿领域的必备知识。
5.1.2 约束的分类
在运动学中,限制条件称为约束 (constraint)。
假如研究的物体对象由 n n n 个质点组成, 那么在三维空间中, 取第 i i i 个质点的位矢 r ⃗ i \vec{r}_i r i, i = 1 , 2 , ... , n i = 1,2,\dots,n i=1,2,...,n, 其正交分量为 x i , y i , z i x_i,y_i,z_i xi,yi,zi。
如果约束方程不显含时间, 即
f = f ( r ⃗ 1 , ... , r ⃗ n ) , f = f(\vec{r}_1, \dots, \vec{r}_n), f=f(r 1,...,r n),
则称其为定常约束或稳定约束;
如果约束方程显含时间, 即
f = f ( t , r ⃗ 1 , ... , r ⃗ n ) , f = f(t, \vec{r}_1, \dots, \vec{r}_n), f=f(t,r 1,...,r n),
则称其为非定常约束或非稳定约束。
可解约束与不可解约束
(解:解脱)

一般化:
不可解约束
f ( r ⃗ 1 , ... , r ⃗ n ; r ⃗ ˙ 1 , ... , r ⃗ ˙ n ; t ) = 0 f(\vec{r}_1, \dots, \vec{r}_n; \dot{\vec{r}}_1, \dots, \dot{\vec{r}}_n; t) = 0 f(r 1,...,r n;r ˙1,...,r ˙n;t)=0
可解约束
f ( r ⃗ 1 , ... , r ⃗ n ; r ⃗ ˙ 1 , ... , r ⃗ ˙ n ; t ) ≥ 0 f(\vec{r}_1, \dots, \vec{r}_n; \dot{\vec{r}}_1, \dots, \dot{\vec{r}}_n; t) \geq 0 f(r 1,...,r n;r ˙1,...,r ˙n;t)≥0
几何约束与微分约束
几何约束
f ( r ⃗ 1 , ... , r ⃗ n ; t ) = 0 f(\vec{r}_1, \dots, \vec{r}n; t) = 0 f(r 1,...,r n;t)=0
d f d t = 0 ⟶ ∂ f ∂ t + ∑ i = 1 n ( ∂ f ∂ x x ˙ + ∂ f ∂ y y ˙ + ∂ f ∂ z z ˙ ) = 0 \frac{df}{dt} = 0 \longrightarrow \frac{\partial f}{\partial t} + \sum{i=1}^{n} \left( \frac{\partial f}{\partial x} \dot{x} + \frac{\partial f}{\partial y} \dot{y} + \frac{\partial f}{\partial z} \dot{z} \right) = 0 dtdf=0⟶∂t∂f+i=1∑n(∂x∂fx˙+∂y∂fy˙+∂z∂fz˙)=0
- 限制位置,必然限制速度
- 几何约束可以通过求导变成微分约束
微分约束
f ( r ⃗ 1 , ... , r ⃗ n ; r ⃗ ˙ 1 , ... , r ⃗ ˙ n ; t ) = 0 f(\vec{r}_1, \dots, \vec{r}_n; \dot{\vec{r}}_1, \dots, \dot{\vec{r}}_n; t) = 0 f(r 1,...,r n;r ˙1,...,r ˙n;t)=0
- 可积分的微分约束 x ˙ − y ˙ = 0 ⟶ x − y = C \dot{x} - \dot{y} = 0 \longrightarrow x - y = C x˙−y˙=0⟶x−y=C
(限制速度,也限制位置) - 不可积分的微分约束 x ˙ − y ˙ z = 0 ⟶ d x − z d y = 0 \dot{x} - \dot{y}z = 0 \longrightarrow dx - zdy = 0 x˙−y˙z=0⟶dx−zdy=0
(限制速度,不限制位置) z ( y ) = ? z(y) = ? z(y)=?
几何约束不显含速度。
显含速度的约束叫做微分约束,含有对时间的导数。
可积分的微分约束,例如:
x ˙ − y ˙ = C \dot{x} - \dot{y}= C x˙−y˙=C
进行积分:
∫ ( x ˙ − y ˙ ) d t = ∫ x ˙ d t − ∫ y ˙ d t = x − y = ∫ C d t = C t \int (\dot{x} - \dot{y}) dt = \int \dot{x}dt - \int \dot{y}dt = x-y= \int C dt=Ct ∫(x˙−y˙)dt=∫x˙dt−∫y˙dt=x−y=∫Cdt=Ct
可积分约束也是完整约束。
不可积分的约束叫做非完整约束。
5.1.3 广义坐标
Lagrange 首先用符号 q α q_\alpha qα 表示第 α \alpha α 个广义坐标, 其中 α = 1 , 2 , ... , s \alpha = 1,2,\dots,s α=1,2,...,s。广义坐标对时间求导, 即得到 q ˙ α \dot{q}_\alpha q˙α, 称为广义速度 (generalized velocity)。
自由度 确定一个系统运动状态所必须的,能够独立变化的物理量的个数
例
| 独立坐标 | 独立速度分量 | 自由度 | |
|---|---|---|---|
| 单个自由质点 | 3个 | 3个 | 3 |
| 约束 x ˙ − y ˙ = 0 \dot{x} - \dot{y} = 0 x˙−y˙=0 | 2个 | 2个 | 2 |
| 约束 x ˙ − y ˙ z = 0 \dot{x} - \dot{y}z = 0 x˙−y˙z=0 | 3个 | 2个 | 2 |
自由度: 3 n − 完整约束的个数 − 不可积分的微分约束的个数 3n - \text{完整约束的个数} - \text{不可积分的微分约束的个数} 3n−完整约束的个数−不可积分的微分约束的个数
这里的 n n n 是指系统里包含的质点个数。
广义坐标 : 能够唯一 确定系统位形的独立 坐标
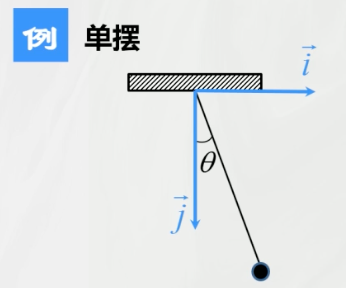
- θ \theta θ 是广义坐标
- ( x , y ) (x, y) (x,y) 不是广义坐标
- 横坐标 x x x 是广义坐标
- 纵坐标 y y y 不是广义坐标
广义坐标的个数 ( s ) : s = 3 n − 完整约束的个数 (s): s = 3n - \text{完整约束的个数} (s):s=3n−完整约束的个数
q 1 , q 2 , ... , q s q_1, q_2, \dots, q_s q1,q2,...,qs
广义速度: q ˙ 1 , q ˙ 2 , ... , q ˙ s \dot{q}_1, \dot{q}_2, \dots, \dot{q}_s q˙1,q˙2,...,q˙s
因为 x x x 能确定 y y y ,所以 ( x , y ) (x,y) (x,y)不是广义坐标。
因为 y y y 所对应的质点的位置不是唯一的,所以 y y y不是广义坐标。
广义坐标的个数 s s s 就是系统的自由度,在分析力学中,这两个概念在数值上是等价的。
虽然 x x x和 θ \theta θ都可以作为广义坐标。但是,这并不意味着广义坐标个数至少为2。因为 x x x和角度 θ \theta θ存在函数关系不是独立变量。
系统自由度分析(广义坐标个数)
在这个系统中,我们研究的对象是那个挂在绳子末端的小球。因此,质点数 n = 1 n = 1 n=1。如果没有约束,这个小球在三维空间中有 3 n = 3 3n = 3 3n=3 个自由度(即可以沿 x , y , z x, y, z x,y,z 任意移动)。
它受到了 2 个主要的完整约束:
- 绳长约束(几何约束):小球到悬挂点的距离必须等于绳长 l l l。用方程表示就是: x 2 + y 2 + z 2 = l 2 x^2 + y^2 + z^2 = l^2 x2+y2+z2=l2。这消耗了 1 个自由度。
- 平面运动约束:单摆通常被限制在一个固定的平面内摆动(例如图中的 i − j i-j i−j 平面)。这意味着垂直于该平面的坐标(假设为 z z z)必须为 0,即 z = 0 z = 0 z=0。这又消耗了 1 个自由度。
所以,总的完整约束个数 k = 2 k = 2 k=2。
计算广义坐标的个数 s s s套用公式: s = 3 n − k = 3 ( 1 ) − 2 = 1 s = 3n - k = 3(1) - 2 = 1 s=3n−k=3(1)−2=1结果显示,该系统只有 1 个自由度。即广义坐标个数 s = 1 s=1 s=1。
参考资料
- 理论力学(物理类) 主讲:哈尔滨工业大学物理学院 任延宇 https://www.bilibili.com/video/BV1xJ411s78q
- 理论力学(物理类)(分析力学) https://www.bilibili.com/video/BV1hY411g7HG
- 分析力学 WANG LH https://gtbcamp.cn/notes/analytical-mechanics/analytical-mechanics.pdf
- 《经典力学》纸质书 高显