【初阶数据结构03】——单链表专题

文章目录

引言

[1. 链表的概念及结构](#1. 链表的概念及结构)

[1.1 什么是链表？](#1.1 什么是链表？)

[1.2 节点的定义](#1.2 节点的定义)

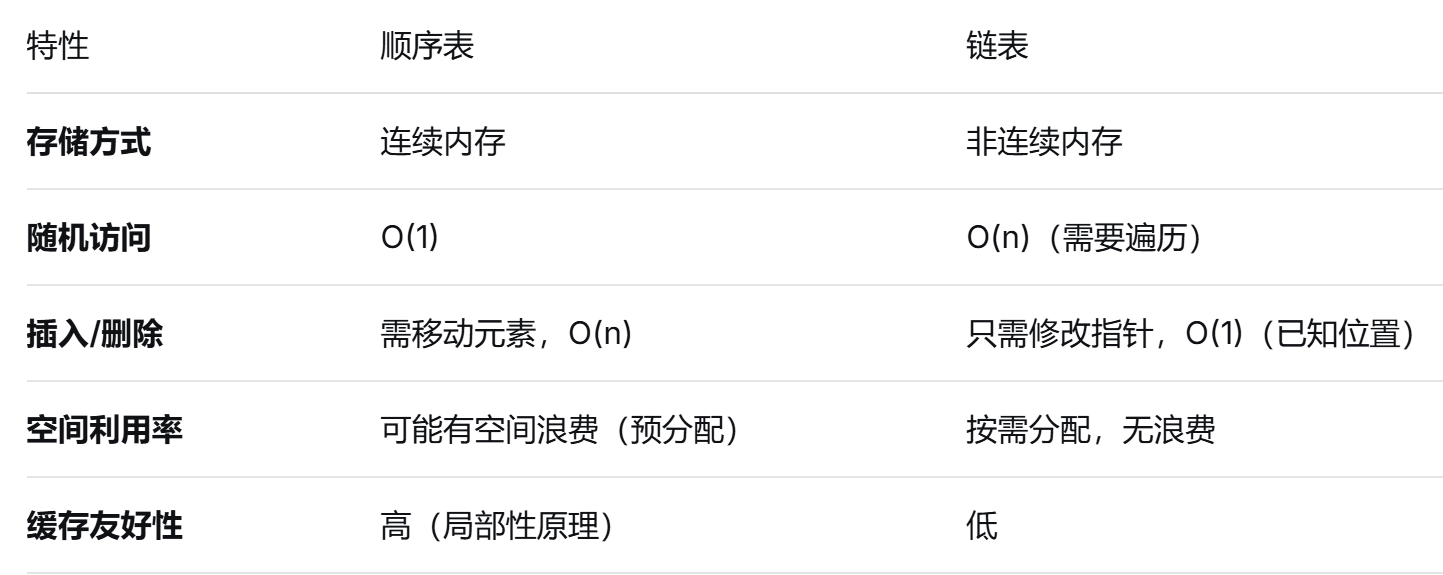
[1.3 链表与顺序表的对比](#1.3 链表与顺序表的对比)

[2. 单链表的实现](#2. 单链表的实现)

[2.1 头文件定义 (SList.h)](#2.1 头文件定义 (SList.h))

[2.2 函数实现 (SList.c)](#2.2 函数实现 (SList.c))

[2.2.1 打印链表](#2.2.1 打印链表)

[2.2.2 创建新节点（内部辅助函数）](#2.2.2 创建新节点（内部辅助函数）)

[2.2.3 尾部插入](#2.2.3 尾部插入)

[2.2.4 头部插入](#2.2.4 头部插入)

[2.2.6 头部删除](#2.2.6 头部删除)

[2.2.7 查找](#2.2.7 查找)

[2.2.8 指定位置之前插入数据](#2.2.8 指定位置之前插入数据)

[2.2.9 指定位置之后的插入](#2.2.9 指定位置之后的插入)

[2.2.10 删除指定位置的节点](#2.2.10 删除指定位置的节点)

[2.2.11 删除指定位置之后的节点](#2.2.11 删除指定位置之后的节点)

[2.3 测试代码示例](#2.3 测试代码示例)

[3. 链表的分类](#3. 链表的分类)

[3.1 单向 / 双向](#3.1 单向 / 双向)

[3.2 带头 / 不带头](#3.2 带头 / 不带头)

[3.3 循环 / 非循环](#3.3 循环 / 非循环)

[4. 链表与顺序表的对比思考](#4. 链表与顺序表的对比思考)

为什么需要链表？

链表的代价

如何选择？

[5. 后续预告：基于单链表实现通讯录](#5. 后续预告：基于单链表实现通讯录)

总结

引言

在上一篇文章中，我们学习了顺序表，它像一列固定编组的火车，车厢紧密相连，可以快速找到任何一节车厢，但想要在中间加一节或拆掉一节，就得大动干戈。今天我们要介绍的单链表，则像一列灵活的货运火车------每节车厢独立存在，车厢之间通过"钥匙"连接，你可以轻松地在任意位置挂载或卸下车厢，而不影响其他部分。

链表是数据结构中极其重要的一环，它解决了顺序表在插入、删除时效率低下的问题，是后续学习更复杂数据结构（如树、图）的基础。'

1. 链表的概念及结构

1.1 什么是链表？

链表是一种物理存储结构上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。

理解这句话，我们可以用火车作比喻：

每节车厢是独立的，它在内存中单独申请空间（就像火车车厢可以在工厂独立制造）
车厢之间通过连接器相连（指针），前一辆车知道后一辆车的位置
整列火车的逻辑顺序由这些连接器决定，而不依赖物理位置

在内存中，链表的节点可能是东一块、西一块，但通过指针，我们依然能按顺序访问它们。

1.2 节点的定义

链表中的每个元素称为节点（Node），它包含两部分：

数据域：存储实际的数据
指针域：存储下一个节点的地址

用C语言结构体可以这样表示：

cpp 复制代码

typedef int SLdatatype;
typedef struct SListNode//链表的节点结构
{
	SLdatatype data;
	struct SListNode* nextnode;
}SLnode;

next指针就像"钥匙"，拿着它就能找到下一节车厢。如果当前节点是最后一节，则next置为NULL。

大概结构：

1.3 链表与顺序表的对比

2. 单链表的实现

我们将实现一个不带头结点的单链表，提供常见的操作接口。为了代码复用，我们会使用typedef定义数据类型。

2.1 头文件定义 (SList.h)

cpp 复制代码

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int SLdatatype;
typedef struct SListNode//链表的节点结构
{
	SLdatatype data;
	struct SListNode* nextnode;
}SLnode;
void PrintSList(SLnode* head);//一个输出链表的函数
SLnode* Createnewnode(SLdatatype n);//一个创建新节点的函数
void SListpushback(SLnode** head, SLdatatype n);//在链表最后插入新节点
void SListpushfront(SLnode** head, SLdatatype n);//在链表头部插入新节点
void SListpopback(SLnode** head);//删除最后一个节点
void SListpopfront(SLnode** head);//删除最后一个节点
SLnode* SListfind(SLnode* head, SLdatatype n);//查找链表中是否有某个值
//在指定位置之前插入数据
void SListinsert(SLnode** head,SLnode* pos, SLdatatype n);
//在指定位置之后插入数据
void SListinsertAfter(SLnode* pos, SLdatatype n);
//删除指定节点
void SListdelete(SLnode** head, SLnode* pos);
//删除指定节点之后的节点
void SListdeleteAfter(SLnode* pos);
//销毁链表
void SListdestroy(SLnode** head);

2.2 函数实现 (SList.c)

2.2.1 打印链表

cpp 复制代码

void PrintSList(SLnode* head)//先写出打印链表的函数，用于测试代码
{
	SLnode* p = head;
	while (p)
	{
		printf("%d->", p->data);
		p = p->nextnode;
	}
	printf("NULL\n");
}

写完打印链表的函数之后可以在测试文件中创建几个节点，并将其连接起来，打印以观察链表结构创建是否正确。

cpp 复制代码

SLnode* head = (SLnode*)malloc(sizeof(SLnode));
head->data = 1;
SLnode* node1 = (SLnode*)malloc(sizeof(SLnode));
node1->data = 2;
SLnode* node2 = (SLnode*)malloc(sizeof(SLnode));
node2->data = 3;
SLnode* node3 = (SLnode*)malloc(sizeof(SLnode));
node3->data = 4;
head->nextnode=node1;
node1->nextnode=node2;
node2->nextnode=node3;
node3->nextnode=NULL;
PrintSList(head);

2.2.2 创建新节点（内部辅助函数）

cpp 复制代码

SLnode* Createnewnode(SLdatatype n)//一个创建新的节点的函数
{
	SLnode* newnode = (SLnode*)malloc(sizeof(SLnode));
	if (newnode == NULL)
	{
		perror("malloc error");
		exit(1);
	}
	newnode->data = n;
	newnode->nextnode = NULL;
	return newnode;
}

为了方便后续代码编写，直接写出一个创建新节点的函数。

2.2.3 尾部插入

cpp 复制代码

void SListpushback(SLnode** head, SLdatatype n)
{
	assert(head!= NULL);
	//有空链表还有非空链表两种情况
	SLnode* newnode= Createnewnode(n);
	SLnode* pr = *head;
	if (*head == NULL)//如果是空链表
	{
		*head = newnode;
		return;
	}
	else
	{
		while ((pr)->nextnode)
		{
			pr = (pr)->nextnode;
		}
		(pr)->nextnode = newnode;
	}
}

**思路：**当链表为非空链表时，将最后一个节点指向新节点，然后新节点指向空。

当链表为空链表时，将新节点作为头节点。

2.2.4 头部插入

cpp 复制代码

void SListpushfront(SLnode** head, SLdatatype n)
{
	assert(head);
	SLnode* newnode = Createnewnode(n);
	newnode->nextnode = *head;
	*head = newnode;
}

**思路：**将新节点的nextnode指向头节点，并将头节点进行更新。

2.2.5 尾部删除

cpp 复制代码

void SListpopback(SLnode** head)
{
	assert(head);
	if ((*head)->nextnode == NULL)//这里如果只有一个节点就直接释放该节点
	{
		free(*head);
	}
	else//否则就找到最后一个节点，然后释放它，然后把前面节点的next指针指向NULL
	{
		SLnode* pcur = (*head)->nextnode;
		SLnode* bfpcur = *head;
		while (pcur->nextnode)
		{
			bfpcur = bfpcur->nextnode;
			pcur = pcur->nextnode;
		}
		free(pcur);
		bfpcur->nextnode = NULL;
	}
}

**思路：**如果链表中只有一个头节点，那么就释放头节点就行了，要么就是创建两个指针，遍历整个链表，一个指针（pcur)指向最后一个节点，另一个指针（bfpcur)指向前一个节点，释放最后一个节点的空间，让（bfpcur)的nxtnode指向NULL。

2.2.6 头部删除

cpp 复制代码

void SListpopfront(SLnode** head)
{
	assert(*head);
	SLnode* ppr=*head;
	(*head) = (*head)->nextnode;
	free(ppr);
}

**思路：**创建一个节点用于保存头节点信息释放，然后对头节点进行更新。

2.2.7 查找

在链表中查找数据，如果找到了就返回对应的节点信息，如果没找到就返回空指针

cpp 复制代码

SLnode* SListfind(SLnode* head, SLdatatype n)
{
	SLnode* p = head;
	while (p)
	{
		if (p->data == n)
		{
			return p;
		}
		p = p->nextnode;
	}
	return NULL;
}

**思路：**就是遍历整个链表，然后用条件判断语句进行查找。

2.2.8 指定位置之前插入数据

cpp 复制代码

void SListinsert(SLnode** head, SLnode* pos, SLdatatype n)
{
	assert(head);
	SLnode* pnew = Createnewnode(n);
	SLnode* pcur=*head;
	if (pos == *head)
	{
		pnew->nextnode = *head;
		*head = pnew;
		//SListpushfront(head, n);
	}
	else
	{
		while (pcur->nextnode != pos)
		{
			pcur = pcur->nextnode;
		}
		pcur->nextnode = pnew;
		pnew->nextnode = pos;
	}
}

**思路：**如果是在头节点之前插入数据，那么只需要调用头部插入函数即可，其他情况就是找到指定节点前的节点（while (pcur->nextnode != pos)，然后令这个节点的nextnode指向新节点，新节点的nextnode指向指定节点，就完成了指定位置之前的插入。

2.2.9 指定位置之后的插入

cpp 复制代码

void SListinsertAfter(SLnode* pos, SLdatatype n)
{
	assert(pos);
	SLnode* pnew = Createnewnode(n);
	SLnode* pcur = pos->nextnode;
	pos->nextnode = pnew;
	if (pcur)
		pnew->nextnode = pcur;
	else
		pnew->nextnode = NULL;
}

**思路：**这里就是将指定位置的nextnode指向新节点，然后对新节点nextnode的指向进行更新。

2.2.10 删除指定位置的节点

cpp 复制代码

void SListdelete(SLnode** head, SLnode* pos)
{
	assert(head);
	SLnode* pcur=*head;
	if (*head== pos)
	{
		*head = (*head)->nextnode;
		free(pos);
	}
	else
	{
		while (pcur->nextnode != pos)
		{
			pcur = pcur->nextnode;
		}
		pcur->nextnode = pos->nextnode;
		free(pos);
	}
}

**思路：**这里需要对指定位置进行分析，如果指定位置是头节点那么就需要在释放后对头节点进行更新，其他情况就是需要找到两个节点，指定位置以及它前一个的节点，将前一个结点的nextnode更新为指定位置的nextnode，而后释放指定节点。

2.2.11 删除指定位置之后的节点

cpp 复制代码

void SListdeleteAfter(SLnode* pos)
{
	assert(pos && pos->nextnode);
	if ((pos->nextnode)->nextnode == NULL)
	{
		free(pos->nextnode);
		pos->nextnode = NULL;
		return;
	}
	SLnode* pcur = (pos->nextnode)->nextnode;
	free(pos->nextnode);
	pos->nextnode = pcur;
}

**思路：**如果指定位置下一个节点的nextnode为NULL,那么释放之后，指定位置的nextnode就需要更新为NULL，否则就是(pos->nextnode)->nextnode。

2.2.12 销毁链表

cpp 复制代码

void SListdestroy(SLnode** head)
{
	assert(head);
	SLnode* pcur = *head;
	while (pcur)
	{
		SLnode* ptmp = pcur;
		pcur = pcur->nextnode;
		free(ptmp);
	}
	*head = NULL;
}

思路：这里就是遍历整个链表，将所有的节点空间释放掉，最后将head指针设置为空指针。

以上就是链表中基本的增删改查函数代码。

2.3 测试代码示例

cpp 复制代码

#include "SList.h"

int main() {
    SLTNode* list = NULL;

    // 尾部插入
    SLTPushBack(&list, 1);
    SLTPushBack(&list, 2);
    SLTPushBack(&list, 3);
    SLTPrint(list);  // 1 -> 2 -> 3 -> NULL

    // 头部插入
    SLTPushFront(&list, 0);
    SLTPrint(list);  // 0 -> 1 -> 2 -> 3 -> NULL

    // 删除尾部
    SLTPopBack(&list);
    SLTPrint(list);  // 0 -> 1 -> 2 -> NULL

    // 删除头部
    SLTPopFront(&list);
    SLTPrint(list);  // 1 -> 2 -> NULL

    // 查找并插入
    SLTNode* pos = SLTFind(list, 2);
    if (pos) {
        SLTInsertAfter(pos, 3);
        SLTInsert(&list, pos, 1);  // 在2之前插入1
    }
    SLTPrint(list);  // 1 -> 1 -> 2 -> 3 -> NULL? 需要看实际逻辑

    SLTDestroy(&list);
    return 0;
}

3. 链表的分类

链表的结构非常灵活，根据指针方向、是否有头节点、是否循环，可以组合出多种类型。

3.1 单向 / 双向

单向链表：每个节点只包含指向下一个节点的指针，只能单向遍历。
双向链表：每个节点包含指向前一个和后一个节点的指针，可以双向遍历。

3.2 带头 / 不带头

不带头链表：头指针直接指向第一个有效节点。
带头链表 ：存在一个额外的头节点（哨兵位），它不存储有效数据，其next指向第一个有效节点。带头节点可以简化边界处理。

3.3 循环 / 非循环

非循环链表 ：最后一个节点的指针为NULL。
循环链表：最后一个节点的指针指向头节点或第一个节点，形成环。

组合起来共有 2×2×2=82×2×2=8 种链表结构。但在实际应用中，最常用的两种是：

无头单向非循环链表：结构简单，常作为更复杂结构的子结构（如哈希桶、图的邻接表），也是面试笔试的高频考点。
带头双向循环链表 ：结构最复杂，但操作最方便，实际工程中常用它来存储数据（例如C++的std::list）。

4. 链表与顺序表的对比思考

为什么需要链表？

顺序表插入/删除需要移动大量元素，时间复杂度O(n)
顺序表扩容需要重新分配内存并拷贝数据，有一定开销
链表按需分配节点，插入删除只需修改指针，时间复杂度O(1)（已知位置）

链表的代价

不支持随机访问，要访问第i个元素必须遍历，O(n)
每个节点额外存储指针，内存开销稍大
缓存不友好，可能降低程序性能

如何选择？

如果频繁随机访问，且数据量稳定，选顺序表
如果频繁插入删除，且数据量动态变化，选链表
如果既要随机访问又要频繁修改，可能需要结合其他结构（如平衡树、哈希表）

5. 后续预告：基于单链表实现通讯录

在上一篇文章中，我们用顺序表实现了通讯录。现在有了链表，我们可以尝试用单链表重新实现通讯录，并对比两种实现的差异：

添加联系人时，链表不需要考虑扩容
删除联系人时，链表只需要修改指针，效率更高
但查找联系人时，两者都需要遍历，时间复杂度相同

下篇文章，我们将基于单链表实现一个完整的通讯录，并引入文件操作，使数据持久化。

总结

链表由节点组成，节点包含数据和指向下一个节点的指针
链表在物理上不连续，逻辑上通过指针连续
单链表的基本操作包括头插、头删、尾插、尾删、查找、任意位置插入删除等
注意传参时通常需要二级指针，因为可能修改头指针的指向
链表分类多样，最常见的是无头单向非循环链表和带头双向循环链表

掌握单链表是理解更复杂数据结构的关键一步。动手实现一遍，你会对内存管理、指针操作有更深的理解。