VRP 的诞生:一个汽油配送问题和逐层捆绑算法
作者:Sebastilan & Claude(AI 协作)
1959 年,一位数学家和一位石油公司工程师合写了一篇 12 页的论文,定义了一个至今未被完全攻克的问题。
作者:George B. Dantzig

George Bernard Dantzig(1914---2005),美国数学家,线性规划之父。
他最著名的贡献是 1947 年发明的单纯形法(Simplex Method)------这个算法让人类第一次能够系统地求解大规模优化问题,至今仍是商业求解器的核心引擎之一。1975 年获美国国家科学奖章。
关于 Dantzig 有一个广为流传的轶事:1939 年,还是博士生的他上课迟到了,看见导师 Jerzy Neyman 在黑板上写着两道题,以为是作业就拿回去做了。几周后 Neyman 激动地告诉他------那是两个著名的未解统计定理:一个关于 t 检验功效函数的独立性,另一个关于 Neyman-Pearson 基本引理的推广。Dantzig 的证明后来发表在 Annals of Mathematical Statistics 上,并成为他博士论文的一部分。这个故事后来启发了电影《心灵捕手》中的经典黑板场景。

论文的合著者 J.H. Ramser 来自大西洋炼油公司(The Atlantic Refining Company),正是他带来了真实的汽油配送场景------一个油库、十二个加油站、若干辆油罐车。数学家提供方法,工程师提供问题。
G.B. Dantzig, J.H. Ramser. "The Truck Dispatching Problem." Management Science, 6(1):80--91, 1959.
问题:12 个加油站的配送
- 1 个油库(P0):所有油罐车从这里出发,送完货回来
- 12 个加油站(P1 ~ P12):每个站需要补充一定量的汽油
- 油罐车容量:每辆车最多装 6000 加仑
各站的需求量:
| 站点 | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | P11 | P12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 需求 | 1200 | 1700 | 1500 | 1400 | 1700 | 1400 | 1200 | 1900 | 1800 | 1600 | 1700 | 1100 |
任务:设计几条配送路线,让每个站都被送到,每辆车不超载,总路程尽量短。 这就是 CVRP(Capacitated Vehicle Routing Problem)。
各站之间的距离矩阵(论文 Table 1):
| P0 | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | P11 | P12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P0 | 0 | 9 | 14 | 21 | 23 | 22 | 25 | 32 | 36 | 38 | 42 | 50 | 52 |
| P1 | 9 | 0 | 5 | 12 | 22 | 21 | 24 | 31 | 35 | 37 | 41 | 49 | 51 |
| P2 | 14 | 5 | 0 | 7 | 17 | 16 | 23 | 26 | 30 | 36 | 36 | 44 | 46 |
| P3 | 21 | 12 | 7 | 0 | 10 | 21 | 30 | 27 | 37 | 43 | 31 | 37 | 39 |
| P4 | 23 | 22 | 17 | 10 | 0 | 19 | 28 | 25 | 35 | 41 | 29 | 31 | 29 |
| P5 | 22 | 21 | 16 | 21 | 19 | 0 | 9 | 11 | 16 | 22 | 20 | 28 | 30 |
| P6 | 25 | 24 | 23 | 30 | 28 | 9 | 0 | 7 | 11 | 13 | 17 | 25 | 27 |
| P7 | 32 | 31 | 26 | 27 | 25 | 11 | 7 | 0 | 10 | 16 | 10 | 22 | 20 |
| P8 | 36 | 35 | 30 | 37 | 35 | 16 | 11 | 10 | 0 | 6 | 6 | 14 | 16 |
| P9 | 38 | 37 | 36 | 43 | 41 | 22 | 13 | 16 | 6 | 0 | 12 | 20 | 10 |
| P10 | 42 | 41 | 36 | 31 | 29 | 20 | 17 | 10 | 6 | 12 | 0 | 12 | 10 |
| P11 | 50 | 49 | 44 | 37 | 31 | 28 | 25 | 22 | 14 | 20 | 12 | 0 | 10 |
| P12 | 52 | 51 | 46 | 39 | 29 | 30 | 27 | 20 | 16 | 10 | 10 | 10 | 0 |

初始方案:12 辆车各跑一个来回,总距离 2 × 364 = 728 2 \times 364 = 728 2×364=728。接下来的算法就是不断合并路线,减少车辆、缩短总距离。
算法核心:逐层捆绑
Dantzig 和 Ramser 的算法思路简洁------把站点逐层两两绑定:每一层求解一个匹配 LP,把节点配对捆绑成更大的组,绑定后不可拆,交给下一层继续合并。
框架总览
先算一笔总账:
- 总需求 18200 加仑,每车 6000,至少 ⌈ 18200 / 6000 ⌉ = 4 \lceil 18200/6000 \rceil = 4 ⌈18200/6000⌉=4 辆车
- 按需求从小到大堆叠: 1100 + 1200 + 1200 + 1400 = 4900 ≤ 6000 1100 + 1200 + 1200 + 1400 = 4900 \leq 6000 1100+1200+1200+1400=4900≤6000,再加一个 1400 就超了,所以每车最多 4 站
- 从"1 站 1 车"到"最多 4 站 1 车"需要 ⌈ log 2 4 ⌉ = 2 \lceil \log_2 4 \rceil = 2 ⌈log24⌉=2 层合并
| 层级 | 做什么 | 每组最多 | 需求上限 |
|---|---|---|---|
| Level 0 | 初始:每站单独出车 | 1 站 | --- |
| Level 1 | 站点两两配对 | 2 站 | C/2 = 3000 |
| Level 2 | 小组两两合并成路线 | 4 站 | C = 6000 |
两层都做同一件事------求解匹配 LP。Level 1 在 12 个站之间匹配,Level 2 在 Level 1 输出的小组之间匹配。LP 有可能给出小数解("A 和 B 各配了半个"),这时枚举取整即可。
为什么 Level 1 限制需求 ≤ C / 2 \leq C/2 ≤C/2? 因为 Level 2 要把两个小组合并,合并后必须 ≤ C \leq C ≤C。如果每个小组都不超过 C / 2 C/2 C/2,则任意两个小组合并都不会超载。这是保证 Level 2 可行性的简化假设。
Level 1:站点配对
匹配 LP 模型
每个站有一条"连接"------要么连回 P0(单独出车),要么连向另一个站(配对)。可以证明,总距离 = 364 + D = 364 + D =364+D,其中 364 是所有站到 P0 的距离之和(常数), D D D 是这些"连接"的总长度(推导见附录)。最小化 D D D 等价于最小化总距离。
LP 模型:
- N = { 1 , 2 , ... , 12 } \mathcal{N} = \{1, 2, \ldots, 12\} N={1,2,...,12}:站点集合
- E = { ( 0 , i ) : i ∈ N } ∪ { ( i , j ) : i < j , q i + q j ≤ 3000 } \mathcal{E} = \{(0, i) : i \in \mathcal{N}\} \cup \{(i,j) : i < j,\; q_i + q_j \leq 3000\} E={(0,i):i∈N}∪{(i,j):i<j,qi+qj≤3000}:可选边集
- δ ( i ) \delta(i) δ(i):包含站点 i i i 的所有边
min ∑ ( i , j ) ∈ E d i j ⋅ x i j (1) 最小化连接总长 D s.t. ∑ e ∈ δ ( i ) x e = 1 ∀ i ∈ N (2) 每站恰好一条连接 x i j ≥ 0 ∀ ( i , j ) ∈ E (3) 非负 \begin{array}{llll} \min & \displaystyle\sum_{(i,j) \in \mathcal{E}} d_{ij} \cdot x_{ij} & & \text{(1) 最小化连接总长 D} \\[0.8em] \text{s.t.} & \displaystyle\sum_{e \in \delta(i)} x_e = 1 & \forall\, i \in \mathcal{N} & \text{(2) 每站恰好一条连接} \\[0.8em] & x_{ij} \geq 0 & \forall\, (i,j) \in \mathcal{E} & \text{(3) 非负} \end{array} mins.t.(i,j)∈E∑dij⋅xije∈δ(i)∑xe=1xij≥0∀i∈N∀(i,j)∈E(1) 最小化连接总长 D(2) 每站恰好一条连接(3) 非负
P0 的度数不受限------它可以同时"配对"多个站(这些站各自单独出车)。
Gurobi 求解
核心代码很短:
python
import gurobipy as gp
from gurobipy import GRB
m = gp.Model("matching")
m.setParam("OutputFlag", 0)
# 建边:depot 边 + 站间可行配对边
edges = {}
for i in range(1, 13):
edges[(0, i)] = m.addVar(lb=0, ub=1, obj=D[0][i])
for i in range(1, 13):
for j in range(i + 1, 13):
if Q[i] + Q[j] <= 3000:
edges[(i, j)] = m.addVar(lb=0, ub=1, obj=D[i][j])
m.update()
# 每站度 = 1
for i in range(1, 13):
incident = [v for (a, b), v in edges.items() if a == i or b == i]
m.addConstr(gp.quicksum(incident) == 1)
m.optimize()结果
LP 最优 D = 116 D = 116 D=116,对应总距离 364 + 116 = 480 364 + 116 = 480 364+116=480(从初始的 728 降到 480)。这次 LP 恰好给出了整数解 ------所有 x i j x_{ij} xij 不是 0 就是 1,不需要取整。配出 5 对,只留 2 个单独:
| 小组 | 站点 | 需求之和 | d(i,j) |
|---|---|---|---|
| A1 | {P1, P2} | 2900 | 5 |
| A2 | {P3, P4} | 2900 | 10 |
| A3 | {P6, P10} | 3000 | 17 |
| A4 | {P7, P9} | 3000 | 16 |
| A5 | {P11, P12} | 2800 | 10 |
| A6 | {P5} | 1700 | --- |
| A7 | {P8} | 1900 | --- |
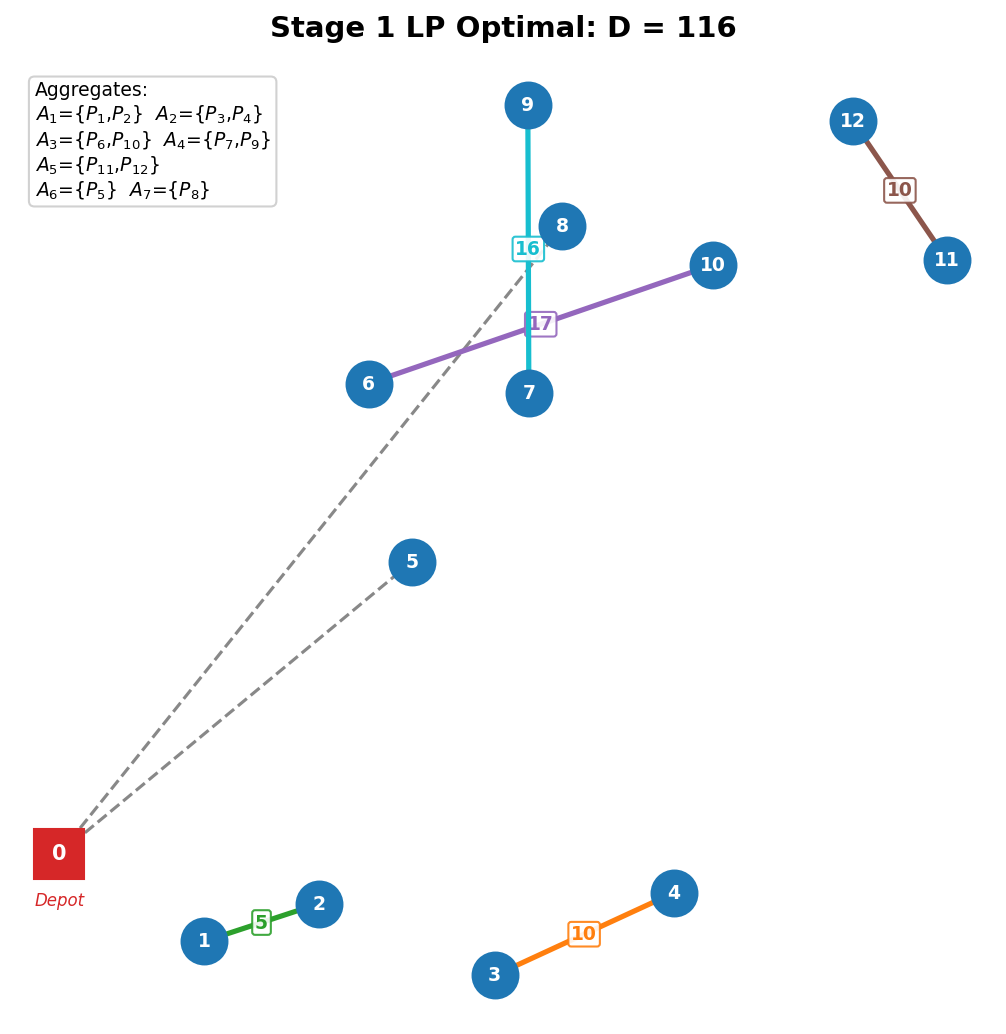
从此刻起,每个配对锁死 ------A1 就是 {P1, P2},意味着它们必须在同一辆车 上,但访问顺序不受约束。Level 2 合并两个小组时,会重新优化所有站点的访问顺序(见下文"组间距离 = mini-TSP")。Level 2 只能在 A1~A7 之间操作。
关键衔接:组间距离 = mini-TSP
Level 2 需要知道"两个小组合并后的路线有多长"。这不是简单地把两段距离加起来------合并后要找最优的访问顺序。
例如 A1={P1,P2} 和 A2={P3,P4} 合并后,一辆车要从 P0 出发经过 4 个站再回来。注意:这里的"绑定"只意味着 P1 和 P2 必须在同一条路线 上(P3、P4 同理),但访问顺序完全自由------车可以 P1→P3→P2→P4 这样交叉访问。因此这确实是一个关于 5 个点(P0 + 4 站)的 TSP。最短路线是什么?穷举排列:
min σ [ d ( P 0 , P σ ( 1 ) ) + d ( P σ ( 1 ) , P σ ( 2 ) ) + d ( P σ ( 2 ) , P σ ( 3 ) ) + d ( P σ ( 3 ) , P σ ( 4 ) ) + d ( P σ ( 4 ) , P 0 ) ] = 54 \min_{\sigma} \big[ d(P_0, P_{\sigma(1)}) + d(P_{\sigma(1)}, P_{\sigma(2)}) + d(P_{\sigma(2)}, P_{\sigma(3)}) + d(P_{\sigma(3)}, P_{\sigma(4)}) + d(P_{\sigma(4)}, P_0) \big] = 54 σmin[d(P0,Pσ(1))+d(Pσ(1),Pσ(2))+d(Pσ(2),Pσ(3))+d(Pσ(3),Pσ(4))+d(Pσ(4),P0)]=54
对应 P0→P1→P2→P3→P4→P0。
对每对小组算一遍 mini-TSP,就得到了 Level 2 的距离矩阵。
Level 2:小组合并
有了 7 个小组和新的距离矩阵,再跑一次同样的匹配 LP------这次容量限制是完整的 6000。
小数解的出现
这次 LP 给出了小数解:A1、A2、A6 三个小组彼此各配了"半个",形成一个三角形纠缠。
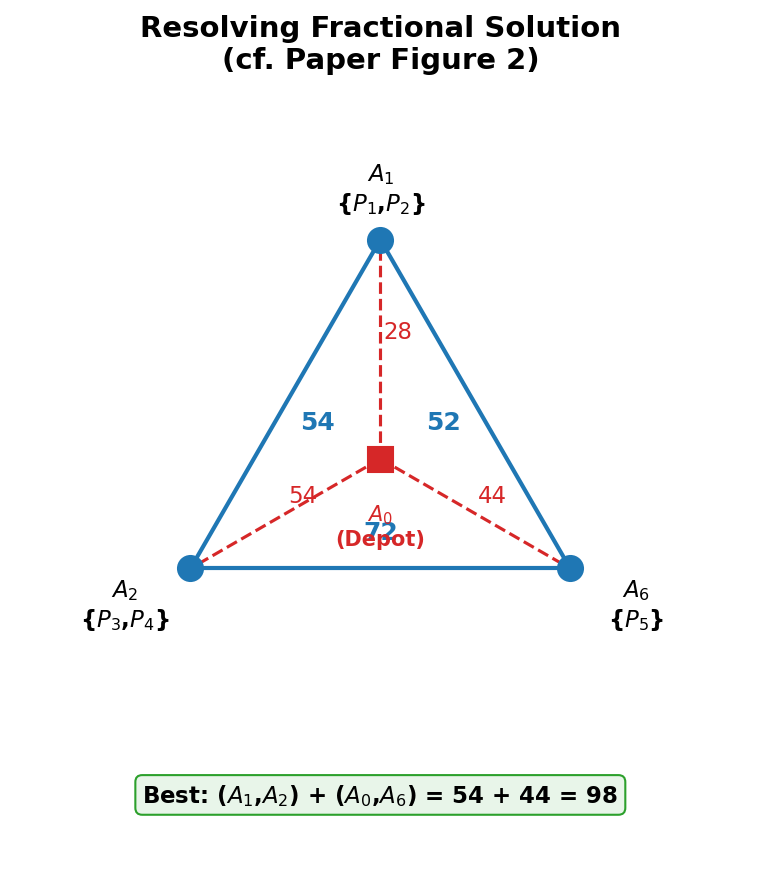
小数解在现实中没有意义,需要取整。三个小组只有三种整数拆法:
| 方案 | 配对 | 单独 | 距离 |
|---|---|---|---|
| ① | A1---A2 (54) | A6 单独 (44) | 98 |
| ② | A1---A6 (52) | A2 单独 (54) | 106 |
| ③ | A2---A6 (72) | A1 单独 (28) | 100 |
方案①最优。加上 LP 已经确定的整数配对(A3---A7,A4---A5),最终得到 4 条路线。
最终结果:4 条路线
| 路线 | 站点 | 最短行驶顺序 | 距离 | 需求 |
|---|---|---|---|---|
| 1 | P1, P2, P3, P4 | P0→P1→P2→P3→P4→P0 | 54 | 5800 |
| 2 | P7, P9, P11, P12 | P0→P7→P11→P12→P9→P0 | 112 | 5800 |
| 3 | P6, P8, P10 | P0→P6→P10→P8→P0 | 84 | 4900 |
| 4 | P5 | P0→P5→P0 | 44 | 1700 |
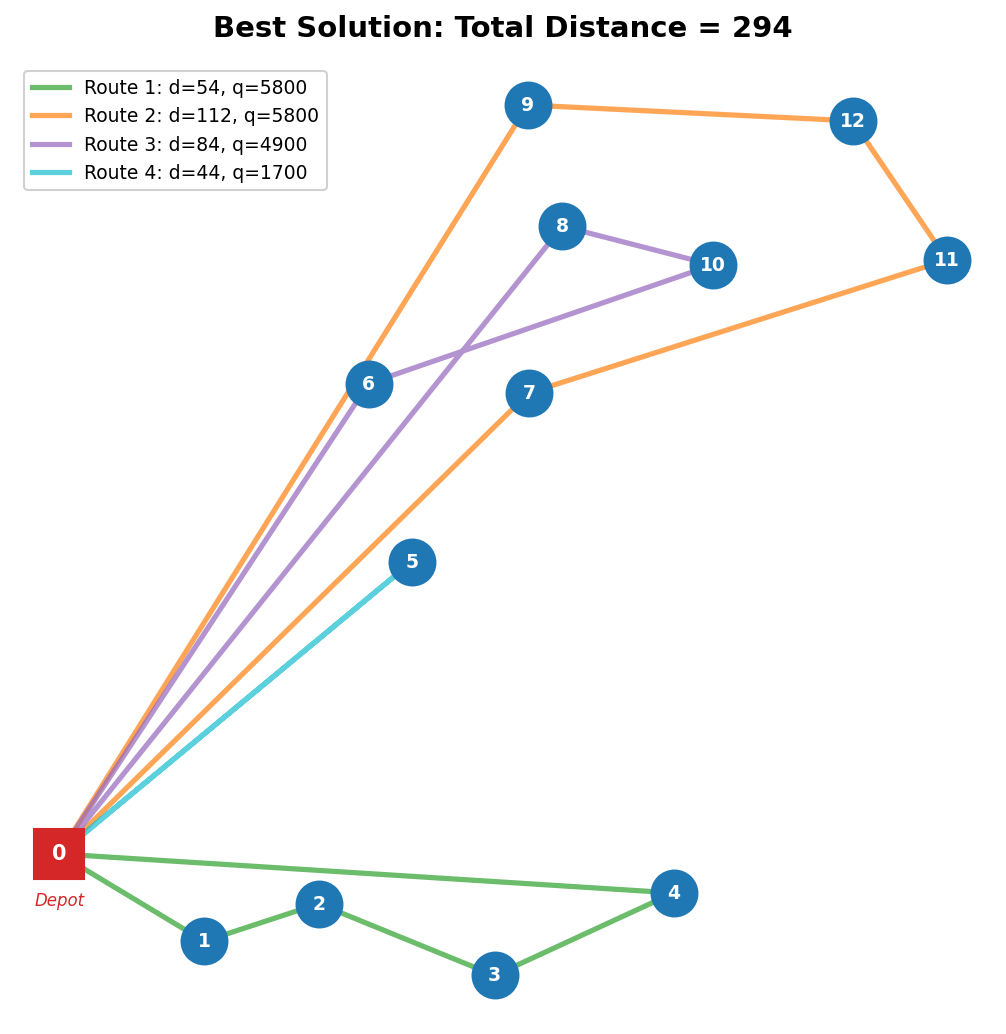
总距离 = 294。
为什么不是最优 290?
论文提到,如果把路线 2 中的 P9 和路线 3 中的 P10 对调:
| 路线 | 算法结果(294) | 调整后(290) |
|---|---|---|
| 2 | {P7, P9, P11, P12} | {P7, P10, P11, P12} |
| 3 | {P6, P8, P10} | {P6, P8, P9} |
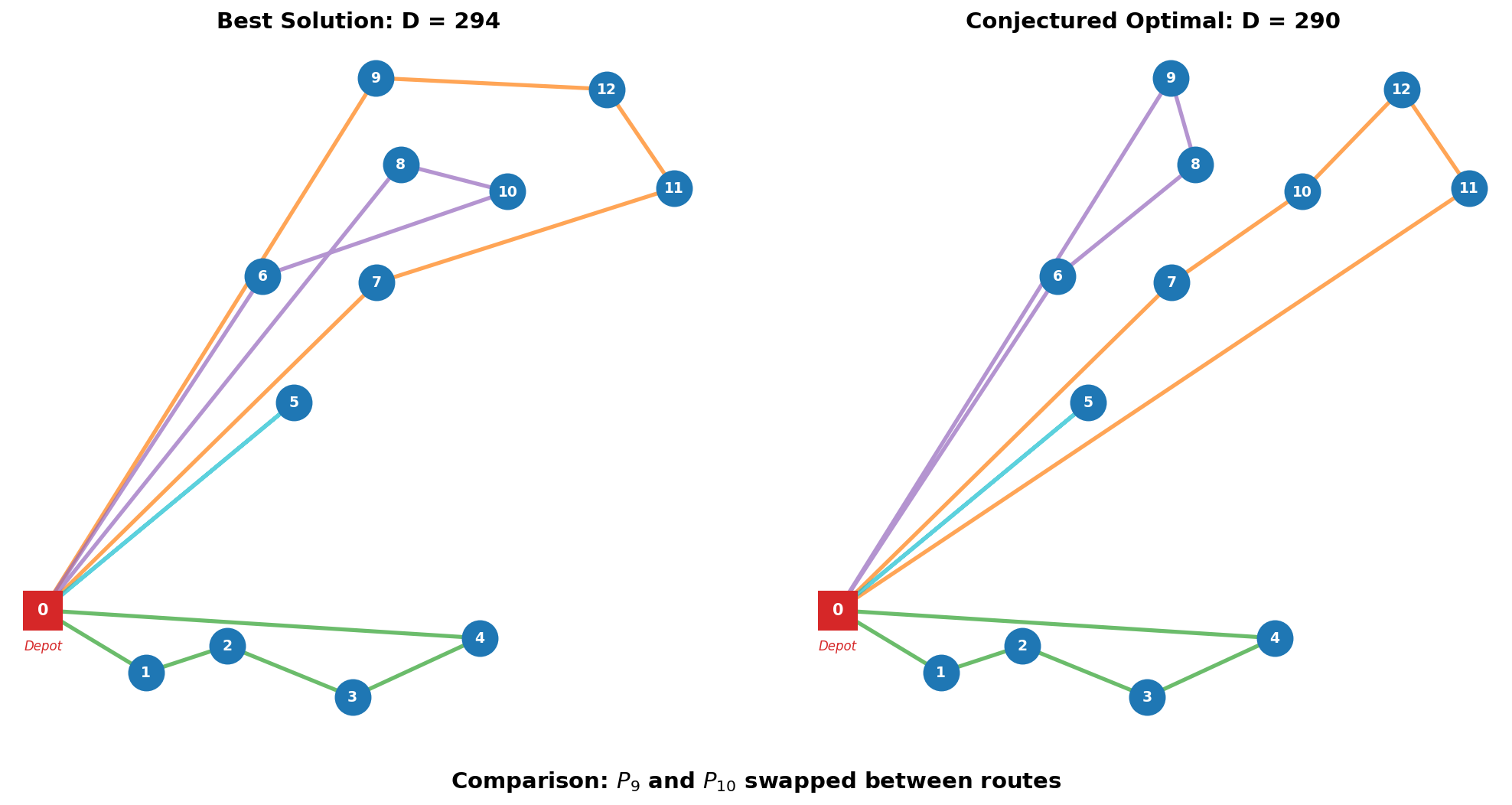
总距离降到 290------但算法无法找到这个解。
原因在于 Level 1 把 P6 和 P10 绑定成了 A3,P7 和 P9 绑定成了 A4。到 Level 2 时这些绑定已不可更改,而最优解 290 需要 P9 和 P10 分属不同路线。逐层锁死的代价就在这里:每一层都是局部最优,但拼起来不一定是全局最优。
回头看:三件开创性的事
1959 年没有个人电脑,大型机也刚刚起步。一个好算法必须能用纸笔和手摇计算器完成------Dantzig 和 Ramser 的逐层捆绑恰好满足这个条件:12 个站的匹配 LP 足够小,可以手工求解。但这篇论文的价值远不止一个算法,它做了三件开创性的事:
- 定义了问题:depot、客户、容量、路线------这套概念框架沿用至今。
- 展示了方法:用数学规划(而非纯经验)来求解调度问题。
- 埋下了种子 :论文中的"配对 + LP"思路,正是后来 Dantzig-Wolfe 分解(1960)的雏形。而 Dantzig-Wolfe 分解演变为列生成,再结合分支定界和切割平面,发展成了今天求解 VRP 最强的精确框架------Branch-Price-and-Cut(BPC)。
从 12 个加油站到现代物流网络,从 1959 年的 12 页论文到今天每年数百篇的 VRP 研究,这条线一直没有断过。
附录:D 与总距离的等价性
总距离可以拆成两部分。配对后,12 个站分为未配对(单独出车)和已配对(共享路线):
总距离 = ∑ 未配对 P m 2 ⋅ d ( P 0 , P m ) + ∑ 已配对 ( P i , P j ) [ d ( P 0 , P i ) + d ( P i , P j ) + d ( P j , P 0 ) ] \text{总距离} = \sum_{\text{未配对 } P_m} 2 \cdot d(P_0, P_m) + \sum_{\text{已配对 } (P_i, P_j)} [d(P_0, P_i) + d(P_i, P_j) + d(P_j, P_0)] 总距离=未配对 Pm∑2⋅d(P0,Pm)+已配对 (Pi,Pj)∑[d(P0,Pi)+d(Pi,Pj)+d(Pj,P0)]
把每一项拆开看------未配对站贡献 d ( P 0 , P m ) + d ( P 0 , P m ) d(P_0, P_m) + d(P_0, P_m) d(P0,Pm)+d(P0,Pm),已配对的一对贡献 d ( P 0 , P i ) + d ( P i , P j ) + d ( P 0 , P j ) d(P_0, P_i) + d(P_i, P_j) + d(P_0, P_j) d(P0,Pi)+d(Pi,Pj)+d(P0,Pj)。每个站都恰好贡献了一个 d ( P 0 , P i ) d(P_0, P_i) d(P0,Pi),提出来:
总距离 = ∑ i = 1 12 d ( P 0 , P i ) ⏟ = 364 + D \text{总距离} = \underbrace{\sum_{i=1}^{12} d(P_0, P_i)}_{= 364} + D 总距离==364 i=1∑12d(P0,Pi)+D
其中 D = ∑ 未配对 d ( P 0 , P m ) + ∑ 已配对 d ( P i , P j ) D = \sum_{\text{未配对}} d(P_0, P_m) + \sum_{\text{已配对}} d(P_i, P_j) D=∑未配对d(P0,Pm)+∑已配对d(Pi,Pj)。364 是常数,因此最小化 D D D 等价于最小化总距离。
初始时 D 0 = 364 D_0 = 364 D0=364(所有站都未配对)。每配一对 ( P i , P j ) (P_i, P_j) (Pi,Pj), D D D 减少 d ( P 0 , P i ) + d ( P 0 , P j ) − d ( P i , P j ) d(P_0, P_i) + d(P_0, P_j) - d(P_i, P_j) d(P0,Pi)+d(P0,Pj)−d(Pi,Pj)------这就是节省量。
附录:完整代码
python
"""
Dantzig & Ramser (1959) --- The Truck Dispatching Problem
========================================================
逐层捆绑算法:严格复现论文中 12 站数值示例。
距离矩阵从 Table 1 提取并经 Table 3 交叉验证。
求解器:Gurobi
"""
import numpy as np
from itertools import permutations
import gurobipy as gp
from gurobipy import GRB
# ============================================================
# 数据:论文 Table 1
# ============================================================
D = np.array([
# P0 P1 P2 P3 P4 P5 P6 P7 P8 P9 P10 P11 P12
[ 0, 9, 14, 21, 23, 22, 25, 32, 36, 38, 42, 50, 52], # P0
[ 9, 0, 5, 12, 22, 21, 24, 31, 35, 37, 41, 49, 51], # P1
[ 14, 5, 0, 7, 17, 16, 23, 26, 30, 36, 36, 44, 46], # P2
[ 21, 12, 7, 0, 10, 21, 30, 27, 37, 43, 31, 37, 39], # P3
[ 23, 22, 17, 10, 0, 19, 28, 25, 35, 41, 29, 31, 29], # P4
[ 22, 21, 16, 21, 19, 0, 9, 11, 16, 22, 20, 28, 30], # P5
[ 25, 24, 23, 30, 28, 9, 0, 7, 11, 13, 17, 25, 27], # P6
[ 32, 31, 26, 27, 25, 11, 7, 0, 10, 16, 10, 22, 20], # P7
[ 36, 35, 30, 37, 35, 16, 11, 10, 0, 6, 6, 14, 16], # P8
[ 38, 37, 36, 43, 41, 22, 13, 16, 6, 0, 12, 20, 10], # P9
[ 42, 41, 36, 31, 29, 20, 17, 10, 6, 12, 0, 12, 10], # P10
[ 50, 49, 44, 37, 31, 28, 25, 22, 14, 20, 12, 0, 10], # P11
[ 52, 51, 46, 39, 29, 30, 27, 20, 16, 10, 10, 10, 0], # P12
])
Q = [0, 1200, 1700, 1500, 1400, 1700, 1400, 1200, 1900, 1800, 1600, 1700, 1100]
CAP = 6000
# ============================================================
# 工具函数
# ============================================================
def mini_tsp(stations, dist_matrix=D):
"""小规模 TSP:穷举所有排列,返回经过 depot(0) + stations 的最短路线距离。"""
if len(stations) == 0:
return 0, []
if len(stations) == 1:
return 2 * dist_matrix[0][stations[0]], list(stations)
best = float('inf')
best_order = None
for perm in permutations(stations):
dist = dist_matrix[0][perm[0]]
for k in range(len(perm) - 1):
dist += dist_matrix[perm[k]][perm[k + 1]]
dist += dist_matrix[perm[-1]][0]
if dist < best:
best = dist
best_order = list(perm)
return best, best_order
def solve_matching_lp(nodes, dist_func, demand, cap_limit):
"""
通用匹配 LP:在 nodes 之间求最小代价匹配。
节点 0 是虚拟 depot(度数不限),nodes 中的每个节点度 = 1。
返回: (pairs, singles, fractional_groups, obj_value)
"""
m = gp.Model("matching")
m.setParam("OutputFlag", 0)
edges = {}
for i in nodes:
edges[(0, i)] = m.addVar(lb=0, ub=1, obj=dist_func(0, i), name=f"x_0_{i}")
for idx_a, i in enumerate(nodes):
for j in nodes[idx_a + 1:]:
if demand[i] + demand[j] <= cap_limit:
edges[(i, j)] = m.addVar(lb=0, ub=1, obj=dist_func(i, j),
name=f"x_{i}_{j}")
m.update()
for i in nodes:
incident = [var for (a, b), var in edges.items() if a == i or b == i]
m.addConstr(gp.quicksum(incident) == 1, name=f"deg_{i}")
m.optimize()
if m.status != GRB.OPTIMAL:
raise RuntimeError(f"LP 求解失败, status={m.status}")
obj_value = m.ObjVal
sol = {k: v.X for k, v in edges.items() if v.X > 1e-8}
# 分类:整数配对 / 单独 / 小数组
pairs, singles, frac_edges = [], [], []
paired_nodes = set()
for (i, j), val in sol.items():
if i == 0:
continue
if abs(val - 1.0) < 1e-6:
pairs.append((i, j))
paired_nodes.update([i, j])
elif val > 1e-8:
frac_edges.append((i, j, val))
for (i, j), val in sol.items():
if i == 0 and abs(val - 1.0) < 1e-6 and j not in paired_nodes:
singles.append(j)
# BFS 找小数解连通分量
fractional_groups = []
if frac_edges:
frac_nodes = set()
for (i, j, _) in frac_edges:
frac_nodes.update([i, j])
remaining = set(frac_nodes)
while remaining:
start = remaining.pop()
component = {start}
queue = [start]
while queue:
node = queue.pop(0)
for (i, j, _) in frac_edges:
other = j if i == node and j in remaining else \
i if j == node and i in remaining else None
if other is not None:
component.add(other)
remaining.discard(other)
queue.append(other)
fractional_groups.append(sorted(component))
return pairs, singles, fractional_groups, obj_value
def build_aggregate_distance(groups, dist_matrix=D):
"""构建组间距离矩阵:每对组的距离 = mini_tsp(组1 ∪ 组2)。"""
n = len(groups)
agg_dist = np.zeros((n + 1, n + 1))
for i in range(n):
d, _ = mini_tsp(groups[i], dist_matrix)
agg_dist[0][i + 1] = d
agg_dist[i + 1][0] = d
for i in range(n):
for j in range(i + 1, n):
combined = groups[i] + groups[j]
d, _ = mini_tsp(combined, dist_matrix)
agg_dist[i + 1][j + 1] = d
agg_dist[j + 1][i + 1] = d
return agg_dist
def resolve_fractional(frac_group, agg_dist, group_names):
"""处理 LP 小数解:枚举取整方案,选最优。"""
best_cost = float('inf')
best_pair = None
best_lone = None
results = []
n = len(frac_group)
for lone_idx in range(n):
lone = frac_group[lone_idx]
remaining = [frac_group[k] for k in range(n) if k != lone_idx]
if len(remaining) == 2:
total = agg_dist[remaining[0]][remaining[1]] + agg_dist[0][lone]
results.append((remaining, lone, total))
if total < best_cost:
best_cost = total
best_pair = tuple(remaining)
best_lone = lone
return best_pair, best_lone, results
# ============================================================
# 主流程
# ============================================================
def main():
print("=" * 60)
print(" Dantzig & Ramser (1959) 逐层捆绑算法")
print("=" * 60)
depot_sum = sum(D[0][i] for i in range(1, 13))
total_demand = sum(Q[1:])
min_vehicles = -(-total_demand // CAP)
print(f"\n总需求: {total_demand}, 容量: {CAP}, 至少 {min_vehicles} 辆车")
# Level 0
print(f"\nLevel 0: 12 条路线,总距离 {2 * depot_sum}")
# Level 1: 站点配对(需求 <= C/2 = 3000)
print("\n" + "=" * 60)
print("Level 1: 站点配对(每组 <= 2 站,需求 <= 3000)")
print("=" * 60)
cap1 = CAP // 2
nodes1 = list(range(1, 13))
demand1 = {i: Q[i] for i in range(13)}
pairs1, singles1, frac1, obj1 = solve_matching_lp(
nodes1, lambda i, j: D[i][j], demand1, cap1
)
print(f"\n LP 最优 D = {obj1:.0f},总距离 = {364 + obj1:.0f}")
for (i, j) in sorted(pairs1):
print(f" {{P{i}, P{j}}} 需求={Q[i]+Q[j]}, d={D[i][j]}")
if singles1:
print(f" 单独: {', '.join(f'P{s}' for s in sorted(singles1))}")
# 构建 aggregates
groups, group_names, group_demands = [], [], []
for (i, j) in sorted(pairs1):
groups.append([i, j])
group_names.append(f"A{len(groups)}={{P{i},P{j}}}")
group_demands.append(Q[i] + Q[j])
for s in sorted(singles1):
groups.append([s])
group_names.append(f"A{len(groups)}={{P{s}}}")
group_demands.append(Q[s])
# 组间距离
agg_dist = build_aggregate_distance(groups)
# Level 2: 小组合并(需求 <= C = 6000)
print("\n" + "=" * 60)
print("Level 2: 小组合并(需求 <= 6000)")
print("=" * 60)
n_groups = len(groups)
nodes2 = list(range(1, n_groups + 1))
demand2 = {0: 0}
for i in range(n_groups):
demand2[i + 1] = group_demands[i]
pairs2, singles2, frac2, obj2 = solve_matching_lp(
nodes2, lambda i, j: agg_dist[i][j], demand2, CAP
)
if frac2:
print(f" 出现小数解,枚举取整:")
for fg in frac2:
pair, lone, results = resolve_fractional(fg, agg_dist, group_names)
for idx, (rem, ln, total) in enumerate(results):
marker = " <--" if (rem[0], rem[1]) == (pair[0], pair[1]) else ""
print(f" 方案{chr(9312+idx)}: "
f"{group_names[rem[0]-1]}-{group_names[rem[1]-1]} + "
f"{group_names[ln-1]}单独 = {total:.0f}{marker}")
pairs2.append(pair)
singles2.append(lone)
# 最终结果
print("\n" + "=" * 60)
print("最终路线")
print("=" * 60)
total_distance = 0
route_num = 0
for (ai, aj) in pairs2:
route_num += 1
stations = groups[ai - 1] + groups[aj - 1]
dist, order = mini_tsp(stations)
total_distance += dist
demand = sum(Q[s] for s in stations)
route_str = " -> ".join([f"P{s}" for s in order])
print(f" 路线 {route_num}: P0 -> {route_str} -> P0 "
f"距离={dist} 需求={demand}")
for ai in singles2:
route_num += 1
stations = groups[ai - 1]
dist, order = mini_tsp(stations)
total_distance += dist
demand = sum(Q[s] for s in stations)
route_str = " -> ".join([f"P{s}" for s in order])
print(f" 路线 {route_num}: P0 -> {route_str} -> P0 "
f"距离={dist} 需求={demand}")
print(f"\n 总距离: {total_distance}")
if __name__ == "__main__":
main()附录:标准算例 Benchmark
将论文的逐层捆绑算法推广到标准 CVRP 算例,LP 求解器使用 Gurobi,mini-TSP 使用 LKH(Lin-Kernighan-Helsgott 启发式,通过 elkai 调用)。层数严格按论文公式确定:先算每辆车最多能装几个站 t t t(按需求从小到大贪心填装),然后 L = ⌈ log 2 t ⌉ L = \lceil \log_2 t \rceil L=⌈log2t⌉。
关于 mini-TSP 的正确性:逐层捆绑中的"绑定"只约束哪些站必须同车,不约束访问顺序 。论文 Section 3.5 原文给出了明确的例子:合并 {P6, P10} 和 {P7, P9} 时,最短路线是 P0→P6→P7 →P10→P9 →P0------两组站点交叉访问,并不要求同组站点相邻。因此计算合并后的路线距离就是一个标准 TSP。
通用求解器代码和 115 个标准 CVRP 测试实例已开源:GitHub - Sebastilan/blog/vrp-papers/dantzig-1959
| 实例 | 客户数 | 车辆数 | 容量 | Dantzig | 最优解 | Gap | 耗时 |
|---|---|---|---|---|---|---|---|
| E-n13-k4 | 12 | 4 | 6000 | 294 | 247 | 19.0% | 0.1s |
| P-n16-k8 | 15 | 8 | 35 | 461 | 450 | 2.4% | 0.0s |
| P-n19-k2 | 18 | 2 | 160 | 236 | 212 | 11.3% | 0.1s |
| P-n20-k2 | 19 | 2 | 160 | 232 | 216 | 7.4% | 0.1s |
| P-n21-k2 | 20 | 2 | 160 | 234 | 211 | 10.9% | 0.1s |
| E-n22-k4 | 21 | 4 | 6000 | 472 | 375 | 25.9% | 0.1s |
| P-n22-k2 | 21 | 2 | 160 | 247 | 216 | 14.4% | 0.2s |
| P-n22-k8 | 21 | 8 | 3000 | 680 | 590 | 15.3% | 0.1s |
| E-n23-k3 | 22 | 3 | 4500 | 570 | 569 | 0.2% | 0.2s |
| P-n23-k8 | 22 | 8 | 40 | 583 | 529 | 10.2% | 0.1s |
| E-n30-k3 | 29 | 3 | 4500 | 532 | 503 | 5.8% | 0.3s |
| B-n31-k5 | 30 | 5 | 100 | 756 | 672 | 12.5% | 0.3s |
| E-n31-k7 | 30 | 7 | 140 | 1386 | 1212 | 14.4% | 0.2s |
| A-n32-k5 | 31 | 5 | 100 | 1001 | 784 | 27.7% | 0.3s |
| A-n33-k5 | 32 | 5 | 100 | 737 | 661 | 11.5% | 0.3s |
| A-n33-k6 | 32 | 6 | 100 | 910 | 742 | 22.6% | 0.3s |
| E-n33-k4 | 32 | 4 | 8000 | 1061 | 835 | 27.1% | 0.3s |
| A-n34-k5 | 33 | 5 | 100 | 861 | 778 | 10.7% | 0.4s |
| B-n34-k5 | 33 | 5 | 100 | 827 | 788 | 4.9% | 0.3s |
| B-n35-k5 | 34 | 5 | 100 | 1216 | 955 | 27.3% | 0.4s |
| A-n36-k5 | 35 | 5 | 100 | 1026 | 799 | 28.4% | 0.4s |
| A-n37-k5 | 36 | 5 | 100 | 749 | 669 | 12.0% | 0.4s |
| A-n37-k6 | 36 | 6 | 100 | 1113 | 949 | 17.3% | 0.4s |
| A-n38-k5 | 37 | 5 | 100 | 846 | 730 | 15.9% | 0.5s |
| B-n38-k6 | 37 | 6 | 100 | 931 | 805 | 15.7% | 0.5s |
| A-n39-k5 | 38 | 5 | 100 | 1041 | 822 | 26.6% | 0.4s |
| A-n39-k6 | 38 | 6 | 100 | 1054 | 831 | 26.8% | 0.5s |
| B-n39-k5 | 38 | 5 | 100 | 707 | 549 | 28.8% | 0.6s |
| P-n40-k5 | 39 | 5 | 140 | 533 | 458 | 16.4% | 0.5s |
| B-n41-k6 | 40 | 6 | 100 | 1048 | 829 | 26.4% | 0.6s |
| B-n43-k6 | 42 | 6 | 100 | 964 | 742 | 29.9% | 0.6s |
| A-n44-k6 | 43 | 6 | 100 | 1134 | 937 | 21.0% | 0.6s |
| B-n44-k7 | 43 | 7 | 100 | 1094 | 909 | 20.4% | 0.6s |
| A-n45-k6 | 44 | 6 | 100 | 1101 | 944 | 16.6% | 0.6s |
| A-n45-k7 | 44 | 7 | 100 | 1316 | 1146 | 14.8% | 0.6s |
| B-n45-k5 | 44 | 5 | 100 | 944 | 751 | 25.7% | 0.7s |
| B-n45-k6 | 44 | 6 | 100 | 823 | 678 | 21.4% | 0.6s |
| F-n45-k4 | 44 | 4 | 2010 | 766 | 724 | 5.8% | 0.8s |
| P-n45-k5 | 44 | 5 | 150 | 582 | 510 | 14.1% | 0.6s |
| A-n46-k7 | 45 | 7 | 100 | 1136 | 914 | 24.3% | 0.6s |
| A-n48-k7 | 47 | 7 | 100 | 1377 | 1073 | 28.3% | 0.7s |
| B-n50-k7 | 49 | 7 | 100 | 850 | 741 | 14.7% | 0.8s |
| B-n50-k8 | 49 | 8 | 100 | 1645 | 1312 | 25.4% | 0.8s |
| P-n50-k7 | 49 | 7 | 150 | 676 | 554 | 22.0% | 0.8s |
| P-n50-k8 | 49 | 8 | 120 | 734 | 629 | 16.7% | 0.8s |
| P-n50-k10 | 49 | 10 | 100 | 784 | 696 | 12.6% | 0.7s |
| B-n51-k7 | 50 | 7 | 100 | 1220 | 1016 | 20.1% | 0.8s |
| E-n51-k5 | 50 | 5 | 160 | 621 | 521 | 19.2% | 0.8s |
| P-n51-k10 | 50 | 10 | 80 | 901 | 741 | 21.6% | 0.6s |
49 个实例(客户数 ≤ \leq ≤ 50),平均 Gap 17.8%,最佳 0.2%(E-n23-k3),最差 29.9%(B-n43-k6),大多数在 10%---28% 之间。一个 1959 年的启发式算法,要求可以手算的算法,在 50 个客户以内能稳定给出这样的近似解,在当时已是了不起的成就。
本文是 BPC 学习系列的第一篇。后续文章将从零实现 Branch-Price-and-Cut 求解器,逐步叠加加速策略,每一步都用代码和数据说话。
一起交流
如果你觉得有帮助,欢迎:
- 📌 订阅本专栏,跟进后续更新
- 💬 评论区留言,交流你的想法
- ⭐ 点赞收藏,让更多朋友看到
--- Sebastilan & Claude