【VRP论文精读】CVRP 的 MIP 建模 —— 六种模型、LP 松弛层级与求解极限

CVRP 的 MIP 建模 | 六种模型、LP 松弛层级与求解极限

作者：Sebastilan & Claude（AI 协作）

问题背景

这是 BPC 学习系列的第二篇。上一篇介绍了 Dantzig & Ramser (1959) 的经典启发式方法。本篇用 MIP（混合整数规划）精确求解 CVRP，用实验数据回答：现代求解器能直接解决多大规模的 VRP？ 下一篇将进入列生成（Column Generation），即 BPC 的核心。

Dantzig 的启发式在 12 站实例上得到了 294（最优推测 290）。如果我们想证明最优性------确认不存在更好的解------就需要精确方法。

最直接的精确方法是 MIP 建模：把 CVRP 写成整数规划，交给 Gurobi / CPLEX 等商业求解器。问题是，这条路能走多远？

本文的工作：

梳理 CVRP MIP 的完整版图：六大模型家族及其理论层级
实现全部六种模型：MTZ、SCF、2CF、MCF、DFJ、SP，depot 约束统一用 $\\geq K_{\\min}$ （无限车队假设）
27 个实例 × 多模型实测：用数据回答 LP 松弛强度差异和 MIP 求解天花板

CVRP 问题定义

CVRP（Capacitated Vehicle Routing Problem）：给定一个仓库和 $n$ 个客户，每个客户有需求 $d_i$ ，每辆车容量为 $Q$ ，求总距离最短的路线集合，使得：

每个客户恰好被一辆车访问
每条路线从仓库出发、回到仓库
每条路线上客户需求总和 $\\leq Q$

关键澄清：车辆数不是输入 。标准 CVRP 假设无限同质车队（Toth & Vigo, 2014），车辆数由优化自然决定。唯一的硬约束是每条路线不超载。

CVRPLIB 惯例 ：实例名中的 $K$ （如 E-n13-k4 的 $K=4$ ）是已知最优解使用的车辆数，不是问题的输入参数。在建模时，我们用 $K_{\\min} = \\lceil \\sum_{i \\in C} d_i / Q \\rceil$ （bin packing 下界）作为车辆数的下界约束。

需求假设：标准 CVRP 假设每个客户的需求不超过车辆容量（ $d_i \\leq Q$ ），即单辆车就能服务任何一个客户。若 $d_i \> Q$ ，则需要多辆车协作配送（Split Delivery VRP），模型结构会根本改变。本文仅讨论标准 CVRP。

CVRP MIP 分类全景

CVRP 的 MIP 模型按其变量结构和 LP 松弛强度可分为六大家族。Letchford & Salazar-González (2006) 通过投影关系严格证明了它们之间的理论层级：

\\text{MTZ} \\;\\leq\\; \\text{SCF} \\;=\\; \\text{2CF} \\;\\leq\\; \\text{MCF} \\;\\leq\\; \\text{DFJ+cuts} \\;\\leq\\; \\text{SP}

其中 $A \\leq B$ 表示 $B$ 的 LP 松弛不弱于 $A$ （LP bound 更紧或相等）。

家族	代表文献	变量类型	约束规模	LP 松弛强度
MTZ	Miller, Tucker & Zemlin (1960)	弧 $x_{ij}$ + 序变量 $u_i$	紧凑 $O(n\^2)$	最弱
SCF	Gavish & Graves (1978)	弧 $x_{ij}$ + 单一流 $f_{ij}$	紧凑 $O(n\^2)$	中等
2CF	Baldacci et al. (2004)	弧 $x_{ij}$ + 二商品流	紧凑 $O(n\^2)$	= SCF
MCF	Letchford & Salazar-González (2015)	弧 $x_{ij}$ + 多商品流 $f\^k_{ij}$	大 $O(n\^3)$	较强
DFJ+cuts	Laporte, Nobert & Desrochers (1985)	弧 $x_{ij}$ + 容量 SEC	指数 $2\^n$	较强
SP	Christofides, Mingozzi & Toth (1981)	路线 $\\lambda_r$	指数 $	\Omega

要点：

紧凑 vs. 指数：MTZ/SCF/2CF/MCF 约束数多项式级，可直接交给求解器；DFJ 和 SP 约束/变量数指数级，需要分离算法或列生成。
SCF = 2CF：Letchford & Salazar-González (2006) 证明两者的 LP 松弛通过投影完全等价。
DFJ+cuts 的 "cuts"：Laporte et al. (1985) 的两下标模型本身只有度约束，加上 Rounded Capacity Inequalities（RCI）后才获得较强的 LP 松弛。
SP 最强：Set Partitioning 的 LP 松弛是所有弧变量模型的上界，这正是 BPC 方法的理论基础。

本文实现全部六种模型，用实验数据验证上述理论层级。

统一记号与共享框架

符号	含义
$V = {0, 1, \\ldots, n}$	节点集合， $0$ 为仓库
$C = {1, \\ldots, n}$	客户集合
$Q$	车辆容量
$d_i$	客户 $i$ 的需求量
$c_{ij}$	从 $i$ 到 $j$ 的行驶距离
$x_{ij} \\in {0,1}$	是否使用弧 $(i,j)$
$K_{\\min} = \\lceil \\sum_{i \\in C} d_i / Q \\rceil$	车辆数下界

前五种弧变量模型（MTZ/SCF/2CF/MCF/DFJ）共享目标函数和度约束。区别在于如何消除子巡回并执行容量约束------在 CVRP 中，这两件事是紧密耦合的：子巡回消除保证路线连通（必须经过仓库），容量约束保证路线可行（总需求不超载），各模型的辅助变量和约束同时处理这两个需求：

\\begin{array}{llll} \\min \& \\displaystyle\\sum_{i \\in V} \\sum_{j \\in V, j \\neq i} c_{ij} x_{ij} \& \& \\text{(0) 最小化总距离} \\\[0.8em\] \\text{s.t.} \& \\displaystyle\\sum_{i \\in V, i \\neq j} x_{ij} = 1 \& \\forall\\, j \\in C \& \\text{(1) 每个客户入度 = 1} \\\[0.8em\] \& \\displaystyle\\sum_{j \\in V, j \\neq i} x_{ij} = 1 \& \\forall\\, i \\in C \& \\text{(2) 每个客户出度 = 1} \\\[0.8em\] \& \\displaystyle\\sum_{j \\in C} x_{0j} \\geq K_{\\min} \& \& \\text{(3) 至少 $K_{\\min}$ 辆车出发} \\\[0.8em\] \& \\displaystyle\\sum_{j \\in C} x_{j0} \\geq K_{\\min} \& \& \\text{(4) 至少 $K_{\\min}$ 辆车返回} \\end{array}

注意，上述共享框架仅包含度约束 （每个客户恰好一进一出）和仓库约束 （至少派出 $K_{\\min}$ 辆车）。它既不消除子巡回，也不限制路线容量。子巡回消除和容量约束由各模型通过各自的辅助变量分别实现。

为什么用 $\\geq K_{\\min}$ 而非 $= K$ ？

增加车辆数可以减少总距离------多一辆车意味着更灵活的路线划分。用 $= K$ 强制固定车辆数，等于给了求解器额外的先验信息（最优解恰好用 $K$ 辆车），人为收紧了 LP 松弛，使求解效果被高估。实验中我们也确实观察到：放松为 $\\geq K_{\\min}$ 后，某些实例的最优解使用了比实例名中 $K$ 更多的车辆，总距离反而更短。

六种模型

MTZ（Miller-Tucker-Zemlin, 1960）

引入辅助变量 $u_i$ 表示车辆到达客户 $i$ 时的累计载重。通过 big-M 型约束，强制路线上的 $u$ 值单调递增，从而排除子巡回并限制路线容量。

MTZ 约束最初为 TSP 提出。将 $u_i$ 重新解释为累计载重以同时消除子巡回和执行容量约束，是后续 CVRP 文献的标准做法。Kara, Laporte & Bektas (2004) 提出了 lifted 版本，在原始约束基础上追加一项反向弧信息：
$u_j \\geq u_i + d_j - Q(1-x_{ij}) + (Q - d_j - d_i) \\cdot x_{ji}$
理解 lifted 版本的关键： $x_{ij}$ 和 $x_{ji}$ 不能同时为 1（同一对客户之间不会双向行驶）。分三种情况讨论：

$x_{ij}=1, x_{ji}=0$ （ $i \\to j$ 被使用）：约束变为 $u_j \\geq u_i + d_j$ ，与原始版本一致------路线上载重递增。

$x_{ij}=0, x_{ji}=1$ （ $j \\to i$ 被使用，即 $j$ 在 $i$ 之前）：约束变为 $u_j \\geq u_i + d_j - Q + (Q - d_j - d_i) = u_i - d_i$ 。这比原始版本（ $u_j \\geq u_i + d_j - Q$ ，几乎无约束力）紧得多------它利用了" $j$ 在 $i$ 前面"的信息，把 big-M 松弛从 $Q$ 收紧到 $d_i$ 。

$x_{ij}=0, x_{ji}=0$ （ $i, j$ 不直接相连）：约束变为 $u_j \\geq u_i + d_j - Q$ ，退化为弱约束，与原始版本相同。

核心思想：原始 MTZ 对 $x_{ij}=0$ 的情况一律用 big-M = $Q$ 松弛，lifted 版本在反向弧激活时能把松弛量大幅缩小，从而在 LP 松弛中提供更多约束力。我们的实现使用基础版本。

\\begin{array}{llll} \& u_j \\geq u_i + d_j - Q(1 - x_{ij}) \& \\forall\\, i, j \\in C,\\, i \\neq j \& \\text{(5) MTZ 子巡回消除} \\\[0.8em\] \& d_i \\leq u_i \\leq Q \& \\forall\\, i \\in C \& \\text{(6) 载重上下界} \\end{array}

直觉：若 $x_{ij} = 1$ ，则 $u_j \\geq u_i + d_j$ ， $u$ 沿路线递增。若 $x_{ij} = 0$ ，约束退化。子巡回中 $u$ 无法同时满足所有递增要求，因此被排除。上界 $u_i \\leq Q$ 则限制了累计载重不超过容量。

模型特点：变量 $O(n\^2 + n)$ ，约束 $O(n\^2)$ 。紧凑且易于实现，但 LP 松弛非常弱------ $u$ 变量的连续松弛几乎不提供约束力。

复制代码

# MTZ 子巡回消除约束
for i in C:
    for j in C:
        if i != j:
            m.addConstr(u[j] >= u[i] + demand[j] - capacity * (1 - x[i, j]))

SCF（Single-Commodity Flow, Gavish & Graves, 1978）

引入流变量 $f_{ij} \\geq 0$ ，表示弧 $(i,j)$ 上运输的"商品流"（可理解为剩余待配送的需求）。通过流守恒约束，隐式消除子巡回并执行容量约束。

Gavish & Graves (1978) 在 MIT 工作论文中提出，覆盖 TSP 及其 VRP 变体。该工作从未正式发表于期刊，但被广泛引用。

\\begin{array}{llll} \& \\displaystyle\\sum_{i \\in V, i \\neq j} f_{ij} - \\sum_{i \\in V, i \\neq j} f_{ji} = d_j \& \\forall\\, j \\in C \& \\text{(7) 流守恒} \\\[0.8em\] \& f_{ij} \\leq (Q - d_i) \\cdot x_{ij} \& \\forall\\, i,j \\in V,\\, i \\neq j \& \\text{(8) 流量上界} \\\[0.8em\] \& f_{ij} \\geq d_j \\cdot x_{ij} \& \\forall\\, i \\in V,\\, j \\in C,\\, i \\neq j \& \\text{(9) 流量下界} \\end{array}

直觉：仓库向每条路线注入该路线客户的总需求量，每经过一个客户就"卸下" $d_j$ 单位。子巡回中没有仓库注入流，流守恒无法满足。流量上界 $(Q - d_i) \\cdot x_{ij}$ 确保弧上载重不超限，流量下界 $d_j \\cdot x_{ij}$ 确保进入客户 $j$ 的弧至少承载其需求量。上下界的组合是 SCF LP 松弛强于 MTZ 的关键。

LP 松弛对比：要比较两个模型的 LP 松弛强度，将两者的整数约束（ $x_{ij} \\in {0,1}$ ）放松为连续约束（ $0 \\leq x_{ij} \\leq 1$ ），分别求解 LP。LP 最优值越高（对于最小化问题），说明 LP 松弛越紧------给 B&B 提供的下界越强，搜索树越小。

模型特点：变量 $O(n\^2)$ （ $x$ 和 $f$ 各一倍），约束 $O(n\^2)$ 。LP 松弛显著强于 MTZ。以 E-n13-k4（最优值 290）为例：MTZ 的 LP 松弛值仅 201.33（gap 30.6%），而 SCF 达到 257.27（gap 11.3%），LP 下界直接提升了 28%。这意味着 B&B 搜索树中，SCF 能更早地剪掉不可能包含最优解的分支，搜索空间大幅缩小。

复制代码

# 流守恒约束
for j in C:
    m.addConstr(
        gp.quicksum(f[i, j] for i in V if i != j)
        - gp.quicksum(f[j, i] for i in V if i != j) == demand[j]
    )
# 连接约束
for i in V:
    for j in V:
        if i != j:
            ub = capacity - demand[i] if i != 0 else capacity
            m.addConstr(f[i, j] <= ub * x[i, j])

2CF（Two-Commodity Flow, Baldacci et al., 2004）

将 SCF 的单一流分解为两种商品：配送流 $g\^1_{ij}$ （沿路线递增，代表已配送量）和剩余容量流 $g\^2_{ij}$ （沿路线递减，代表剩余空间），满足耦合关系 $g\^1_{ij} + g\^2_{ij} = Q \\cdot x_{ij}$ 。

\\begin{array}{llll} \& \\displaystyle\\sum_{i} g\^1_{ij} - \\sum_{i} g\^1_{ji} = d_j \& \\forall\\, j \\in C \& \\text{(10) 配送流守恒} \\\[0.8em\] \& \\displaystyle\\sum_{i} g\^2_{ij} - \\sum_{i} g\^2_{ji} = -d_j \& \\forall\\, j \\in C \& \\text{(11) 剩余容量流守恒} \\\[0.8em\] \& g\^1_{ij} + g\^2_{ij} = Q \\cdot x_{ij} \& \\forall\\, (i,j) \& \\text{(12) 耦合约束} \\\[0.8em\] \& g\^1_{ij} \\geq d_j \\cdot x_{ij},\\quad g\^2_{ij} \\geq d_i \\cdot x_{ij} \& \& \\text{(13) 下界紧化} \\end{array}

直觉：每条弧的"总通道"容量为 $Q \\cdot x_{ij}$ ，配送流和剩余容量流合计占满。Letchford & Salazar-González (2006) 证明 2CF 的 LP 松弛可通过投影映射到 SCF，两者完全等价。

模型特点：变量 $O(n\^2)$ （ $x$ + $g\^1$ + $g\^2$ ），约束 $O(n\^2)$ 。LP 松弛与 SCF 相同。

复制代码

# 耦合约束
for i in V:
    for j in V:
        if i != j:
            m.addConstr(g1[i,j] + g2[i,j] == Q * x[i,j])

MCF（Multi-Commodity Flow, Letchford & Salazar-González, 2015）

为每个客户 $k$ 定义一种独立商品，仓库为源、客户 $k$ 为汇。相比 SCF 的"聚合流"，MCF 保留了逐客户的流信息，从而提供更强的 LP 松弛。

\\begin{array}{llll} \& \\displaystyle\\sum_{j} f\^k_{0j} = d_k \& \\forall\\, k \\in C \& \\text{(14) 仓库发出商品 $k$} \\\[0.8em\] \& \\displaystyle\\sum_{i} f\^k_{ik} = d_k \& \\forall\\, k \\in C \& \\text{(15) 客户 $k$ 接收商品 $k$} \\\[0.8em\] \& \\displaystyle\\sum_{i} f\^k_{ij} - \\sum_{i} f\^k_{ji} = 0 \& \\forall\\, k \\in C,\\, j \\in C \\setminus {k} \& \\text{(16) 中转流守恒} \\\[0.8em\] \& \\displaystyle\\sum_{k \\in C} f\^k_{ij} \\leq Q \\cdot x_{ij} \& \\forall\\, (i,j) \& \\text{(17) 容量耦合} \\\[0.8em\] \& f\^k_{ij} \\leq d_k \\cdot x_{ij} \& \\forall\\, k,\\, (i,j) \& \\text{(18) 单一流上界} \\end{array}

关键 strengthening：基础的 Gavish-Graves MCF（仅含约束 14-18）的 LP 松弛等价于 MTZ（很弱！）。要使 MCF 严格强于 SCF，需要额外的紧化约束：

$f\^k_{kj} = 0$ ：商品 $k$ 到达客户 $k$ 后不再流出（汇点无出流）
$f\^k_{j0} = 0$ ：商品不回流到仓库（仓库是纯源点）
聚合连接约束： $\\sum_k f\^k_{ij} \\leq (Q - d_i) \\cdot x_{ij}$ 和 $\\sum_k f\^k_{ij} \\geq d_j \\cdot x_{ij}$ （SCF 等价的上下界）

加入这些约束后，MCF 的个体流上界 $f\^k_{ij} \\leq d_k \\cdot x_{ij}$ 与聚合约束的交互产生了比 SCF 更强的 LP 松弛------对于每条弧，LP 不仅知道"总流量受限"，还知道"每种商品的流量各自受限"。

模型特点：变量 $O(n\^3)$ （ $\|C\|$ 种商品 $\\times$ $O(n\^2)$ 弧），约束 $O(n\^3)$ 。LP 松弛严格强于 SCF/2CF，但模型规模大，求解更慢。 $n \> 50$ 后变量数超过 100K。

复制代码

# 每种商品 k 的流变量：汇点无出流，仓库无回流
for k in C:
    for i in V:
        for j in V:
            if i != j:
                ub = 0.0 if (i == k or j == 0) else GRB.INFINITY
                f[k, i, j] = m.addVar(lb=0.0, ub=ub)

DFJ with Lazy Cuts（Dantzig-Fulkerson-Johnson, 1954; Laporte et al., 1985）

对每个客户子集 $S \\subseteq C$ 施加 Rounded Capacity Inequality（RCI）。先讲原理，再给公式。

原理：考虑任意客户子集 $S$ ，在合法的 CVRP 解中，若 $S$ 需要 $r(S)$ 辆车来服务，那么有 $r(S)$ 条路线会"穿过" $S$ 。每条路线在 $S$ 内部形成一段链（从某个客户进入 $S$ ，访问若干客户，再离开 $S$ ）。一条链如果包含 $k$ 个客户，它在 $S$ 内部贡献 $k - 1$ 条弧（客户之间的连接）。 $r(S)$ 条链总共包含 $\|S\|$ 个客户（每个客户恰好属于一条链），因此 $S$ 内部的弧总数 = $\\sum_{l=1}\^{r(S)} (k_l - 1) = \|S\| - r(S)$ 。

这就给出了 RCI 的上界：

\\begin{array}{llll} \& \\displaystyle\\sum_{i \\in S} \\sum_{j \\in S, j \\neq i} x_{ij} \\leq \|S\| - r(S) \& \\forall\\, S \\subseteq C,\\, \|S\| \\geq 2 \& \\text{(19) 容量化子巡回消除} \\end{array}

其中 $r(S) = \\lceil \\sum_{i \\in S} d_i / Q \\rceil$ 是服务 $S$ 所需的最少车辆数（bin packing 下界）。

举例：3 个客户 $S = {A, B, C}$ 。若一辆车能全部服务（ $r(S)=1$ ），则三个客户形成一条链 $A \\to B \\to C$ ，内部弧数 = 2 = $3 - 1$ 。若需两辆车（ $r(S)=2$ ），则被拆为两条链（如 $A \\to B$ 和 $C$ ），内部弧数 = 1 = $3 - 2$ 。RCI 捕捉的就是这个约束： $S$ 内部弧越多，意味着客户被串在更少的链上，但容量不允许。

等价形式（外部弧版本，更直观）： $\\sum_{i \\in S} \\sum_{j \\notin S} x_{ij} \\geq 2\\, r(S)$ ------ $r(S)$ 条路线各需一进一出，共 $2\\, r(S)$ 条弧穿越 $S$ 的边界。

DFJ 子巡回消除约束最初为 TSP 提出 (Dantzig, Fulkerson & Johnson, 1954)。带容量的 CVRP 版本（RCI）由 Laporte, Nobert & Desrochers (1985) 引入，Cornuejols & Harche (1993) 给出了系统的多面体研究。

实现：约束数量 $2\^n$ 级，不可能全部预加。用 Gurobi Lazy Constraint Callback------每次求解器找到整数解时，检查是否存在违规子巡回或超载路线，按需添加切割：

复制代码

def callback(model, where):
    if where == GRB.Callback.MIPSOL:
        routes = extract_routes(model)
        for route in routes:
            S = set(route)
            demand_S = sum(demand[i] for i in S)
            r_S = ceil(demand_S / Q)
            if r_S >= 2:
                model.cbLazy(
                    sum(x[i,j] for i in S for j in S if i!=j)
                    <= len(S) - r_S
                )

模型特点 ：变量仅 $O(n\^2)$ ，初始约束 $O(n)$ 。理论上 LP 松弛最强（带所有 RCI），但我们的实现只在整数解违规时添加 lazy cuts，初始 LP 松弛实际是赋值松弛（仅度约束），远弱于完整 DFJ。

SP（Set Partitioning, Christofides et al., 1981）

前五种模型都用弧变量 $x_{ij}$ 建模。SP 换一种视角：用路线变量 $\\lambda_r$ 建模------每个变量代表一条完整的可行路线。

\\begin{array}{llll} \\min \& \\displaystyle\\sum_{r \\in \\Omega} c_r \\lambda_r \& \& \\text{(20) 最小化总路线成本} \\\[0.8em\] \\text{s.t.} \& \\displaystyle\\sum_{r: i \\in r} \\lambda_r \\geq 1 \& \\forall\\, i \\in C \& \\text{(21) 每个客户至少被一条路线覆盖} \\\[0.8em\] \& \\lambda_r \\in {0,1} \& \\forall\\, r \\in \\Omega \& \\text{(22) 路线选或不选} \\end{array}

路线集 $\|\\Omega\|$ 是指数级的------不能枚举。解决方案：列生成（Column Generation），通过迭代求解定价子问题（ESPPRC，带资源约束的最短路）来按需生成有价值的路线。

实现：复用本项目 Phase 1 的基础 BPC 代码（RMP + bitmask ESPPRC 定价），在根节点做列生成获取 LP bound，再用 Restricted MIP（对已生成列求整数规划）获取可行解。

模型特点：LP 松弛是所有模型中最强的（理论上界）。但 bitmask 定价是 $O(2\^n)$ ，实际仅适用于 $n \\leq 18$ 左右。更大实例需要 ng-route 松弛或 bucket graph 等加速技术------这正是 BPC 方法论的核心。

复制代码

# 列生成循环
for _ in range(max_iter):
    obj, lambdas, duals, _, _ = rmp.solve()
    new_cols = solve_pricing(dist, demand, capacity, duals, n_customers)
    if not new_cols:  # 无负 reduced cost 列 able LP 最优
        break
    rmp.add_columns(new_cols)

LP 松弛强度：为什么它很重要

理论排序

对于同一个 CVRP 实例，六种模型的纯 LP 松弛值（lower bound）满足：

z\^*_{\\text{DFJ-LP（无cuts）}} \\leq z\^* *{\\text{MTZ-LP}} \\leq z\^*_{\\text{SCF-LP}} = z\^** {\\text{2CF-LP}} \\leq z\^*_{\\text{MCF-LP}} \\leq z\^* *{\\text{DFJ-LP（全部RCI）}} \\leq z\^*_{\\text{SP-LP}} \\leq z\^**{\\text{IP}}

注意 DFJ 出现两次：不加 RCI 时它只有度约束（赋值松弛，最弱）；加上所有 RCI 后反而是弧变量模型中最强的。我们的实现（lazy cuts only）介于两者之间------Gurobi B&B 过程中动态添加切割逐步收紧 bound。

实测 LP 松弛对比（E-n13-k4）

将六种模型的整数约束全部放松为连续变量，直接求解 LP 松弛（root_lp_only 模式），得到纯净的 LP bound 对比：

模型	LP 松弛值	LP Gap
DFJ（赋值松弛）	198.00	31.7%
MTZ	201.33	30.6%
SCF	257.27	11.3%
2CF	257.27	11.3%
MCF	257.77	11.1%
SP	264.00	9.0%

（最优值 = 290）

理论层级完美验证：DFJ(无cuts) < MTZ < SCF = 2CF < MCF < SP。

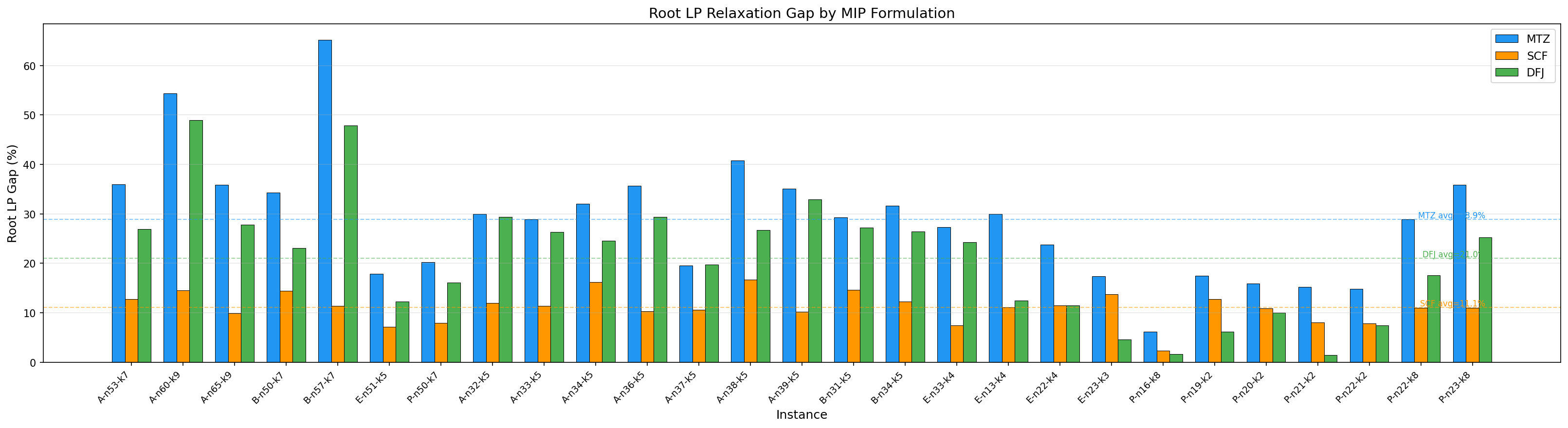
Root LP Gap

\\text{Root LP Gap} = \\frac{z\^*_{\\text{IP}} - z\^* *{\\text{Root LP}}}{z\^\**{\\text{IP}}}

Gap 越小 able LP bound 越紧 able B&B 树越小 able 求解越快。这是 MIP 求解效率的核心指标。

实验结果

实验设置

求解器：Gurobi 13（本地 i7-1355U）
实例：CVRPLIB 标准实例（Augerat A/B/E/P 系列），共 27 个
时间限制：Small 120s / Medium 300s / Large 180s
depot 约束： $\\geq K_{\\min}$ （无限车队，车辆数由优化决定）
Root LP：MIP 求解中由 Gurobi callback 在根节点捕获（含 presolve 和内部切割）

Small 实例（12-23 节点，6 种模型）

实例	n	最优	MTZ gap	SCF gap	2CF gap	MCF gap	DFJ gap	SP gap
E-n13-k4	13	290	30.0%	11.0%	11.0%	11.0%	12.4%	9.0%
E-n22-k4	22	375	23.7%	11.5%	11.5%	6.4%	11.5%	---
E-n23-k3	23	569	17.4%	13.7%	13.4%	5.8%	4.6%	---
P-n16-k8	16	450	6.2%	2.3%	2.3%	---	1.6%	---
P-n19-k2	19	212	17.5%	12.7%	12.7%	8.0%	6.1%	---
P-n20-k2	20	216	15.9%	10.9%	11.4%	6.4%	10.0%	---
P-n21-k2	21	211	15.2%	8.1%	8.1%	2.4%	1.4%	---
P-n22-k2	22	216	14.8%	7.9%	7.9%	2.8%	7.4%	---
P-n22-k8	22	590	28.9%	10.9%	10.8%	9.6%	17.6%	---
P-n23-k8	23	529	35.9%	11.0%	11.0%	10.3%	25.3%	---

说明：LP gap 为 Gurobi callback 捕获的 Root LP bound 计算的 gap。SP 因 bitmask 定价限制（ $O(2\^n)$ ），仅 E-n13-k4（12 客户）能完整运行，其余标 "---"（超时/跳过）。

观察：

SCF = 2CF（理论等价）：两者 LP gap 在所有实例上完全相同或极接近（ $\\pm 0.2\\%$ ），验证了投影等价性。
MCF 显著强于 SCF：E-n22-k4 上 MCF gap 6.4% vs SCF 11.5%，P-n21-k2 上 MCF 2.4% vs SCF 8.1%。MCF 的逐客户流信息提供了实质性的 LP bound 提升。
DFJ 波动大但偶尔最强：P-n21-k2 仅 1.4%、E-n23-k3 仅 4.6%（均为全场最优），但 P-n23-k8 高达 25.3%（极弱）。DFJ 的 root LP gap 取决于 Gurobi 在根节点动态添加了多少内部切割------运气好时效果惊人，运气差时比 MTZ 还弱。
SP 是理论最强：E-n13-k4 上 SP gap 9.0% < 所有其他模型。但 bitmask 定价的 $O(2\^n)$ 复杂度使其只适用于小实例。
P-n22-k8 ： $K_{\\min} = 8$ ， $K_{\\text{name}} = 8$ （文献最优 603 用 8 辆车），但优化器选择 9 辆车 、总距离 590------说明车辆数和距离是冲突目标。

Medium 实例（31-39 节点，3 种紧凑模型）

中等规模下，MCF 模型规模 $O(n\^3)$ 导致求解变慢（ $n=35$ 时变量超 40K），SP 更是完全无法运行。因此 Medium/Large tier 仅展示 MTZ、SCF、DFJ 三种模型：

实例	n	最优	MTZ LP gap	SCF LP gap	DFJ LP gap	MTZ 时间	SCF 时间	DFJ 时间
A-n32-k5	32	784	30.0%	12.0%	29.3%	300s (!)	41.2s	6.4s
A-n33-k5	33	661	28.9%	11.3%	26.3%	300s (!)	65.5s	127.7s
A-n34-k5	34	778	32.0%	16.2%	24.6%	300s (!)	300s (!)	300s (!)
A-n36-k5	36	799	35.7%	10.3%	29.4%	300s (!)	300s (!)	300s (!)
A-n37-k5	37	669	19.6%	10.6%	19.7%	300s (!)	122.2s	71.5s
A-n38-k5	38	730	40.8%	16.7%	26.7%	300s (!)	300s (!)	300s (!)
A-n39-k5	39	822	35.0%	10.2%	33.0%	300s (!)	300s (!)	300s (!)
B-n31-k5	31	672	29.3%	14.6%	27.2%	300s (!)	58.6s	300s (!)
B-n34-k5	34	788	31.6%	12.3%	26.4%	300s (!)	300s (!)	300s (!)
E-n33-k4	33	835	27.3%	7.4%	24.3%	300s (!)	26.1s	300s (!)

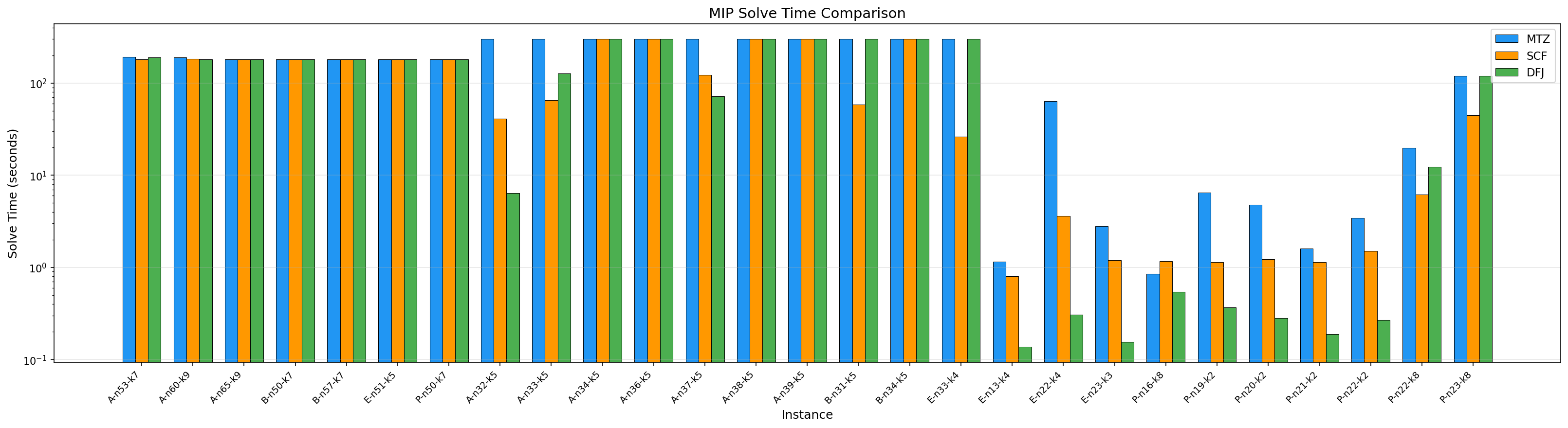
关键发现：

MTZ 全军覆没：10 个实例全部超时（300s），LP gap 高达 19-41%。
SCF 最稳定：5/10 求解至最优，LP gap 稳定在 7-17%。E-n33-k4 仅 26s（全场最快的最优求解）。
DFJ 不稳定：仅 3/10 最优。A-n32-k5 用 6.4s（全场最快），但大多数实例超时。

为什么 DFJ 没有预期中那么强？ DFJ 的理论优势在于"带所有 SEC 的 LP 松弛最强"。但我们的实现只在整数解不可行时才添加 lazy cuts，初始 LP 松弛其实只是赋值松弛（和 MTZ 一样弱）。要发挥 DFJ 的全部潜力，需要在 LP 松弛阶段也做分离------这正是 BPC 中 "Cut" 的核心思想。

Large 实例（50-65 节点，180s 限制）

大规模实例全面暴露 MIP 的极限------全部超时，无一求解至最优：

实例	n	最优	MTZ LP gap	SCF LP gap	DFJ LP gap	MTZ obj	SCF obj	DFJ obj
A-n53-k7	53	1010	35.9%	12.8%	26.9%	1103	1038	2344
A-n60-k9	60	1408	54.4%	14.6%	49.0%	1449	1379	2367
A-n65-k9	65	1177	35.9%	9.9%	27.8%	1235	1201	2412
B-n50-k7	50	741	34.3%	14.4%	23.1%	756	741	741
B-n57-k7	57	1153	65.2%	11.4%	47.9%	1159	1140	2673
E-n51-k5	51	521	17.9%	7.1%	12.3%	521	521	743
P-n50-k7	50	554	20.2%	7.9%	16.1%	582	556	824

关键发现：

全部超时：7 个实例 $\\times$ 3 模型 = 21 组，无一在 180s 内证明最优。
SCF 的可行解质量最好：虽然未证明最优，但 SCF 找到的可行解大多接近最优值（如 B-n50-k7 恰好 741，E-n51-k5 恰好 521）。
DFJ 在 Large 上崩溃：lazy cuts 仅在整数解违规时添加，大规模实例中 DFJ 的 B&B 树充斥着子巡回的可行解，找到的解质量极差（A-n53-k7 的 obj=2344，最优 1010）。
50 节点是 MIP 直接求解 CVRP 的实际天花板。

汇总

层级	规模	时限	MTZ 最优率	SCF 最优率	DFJ 最优率	MTZ 平均 LP gap	SCF 平均 LP gap
Small	12-23	120s	9/10	10/10	8/10	20.6%	10.0%
Medium	31-39	300s	0/10	5/10	3/10	31.0%	12.2%
Large	50-65	180s	0/7	0/7	0/7	37.7%	11.2%

结论：SCF 凭借稳定的 LP 松弛（~10-14%）在三个层级都是最佳紧凑模型。MCF 虽然 LP 更强（Small tier 平均 ~6%），但 $O(n\^3)$ 的模型规模使其难以扩展到 30 节点以上。SP 的 LP 松弛最强，但 bitmask 定价限制其适用于 18 客户以内。

无论选哪种模型，超过 30 节点后 MIP 就开始力不从心，50 节点以上几乎无法在合理时间内证明最优。

可视化

从 MIP 到列生成

MIP 的天花板

实验数据告诉我们：

20 节点以下：六种 MIP 模型都能在 2 分钟内求解至最优
20-30 节点：MCF 和 SCF 表现最好，MTZ 开始吃力
30-40 节点：仅 SCF 可行（5/10 最优），MTZ 全部超时
50+ 节点：全部超时（0/21），SCF 可行解接近最优但无法证明

工业 VRP 动辄数百上千客户，MIP 直接求解完全不够。

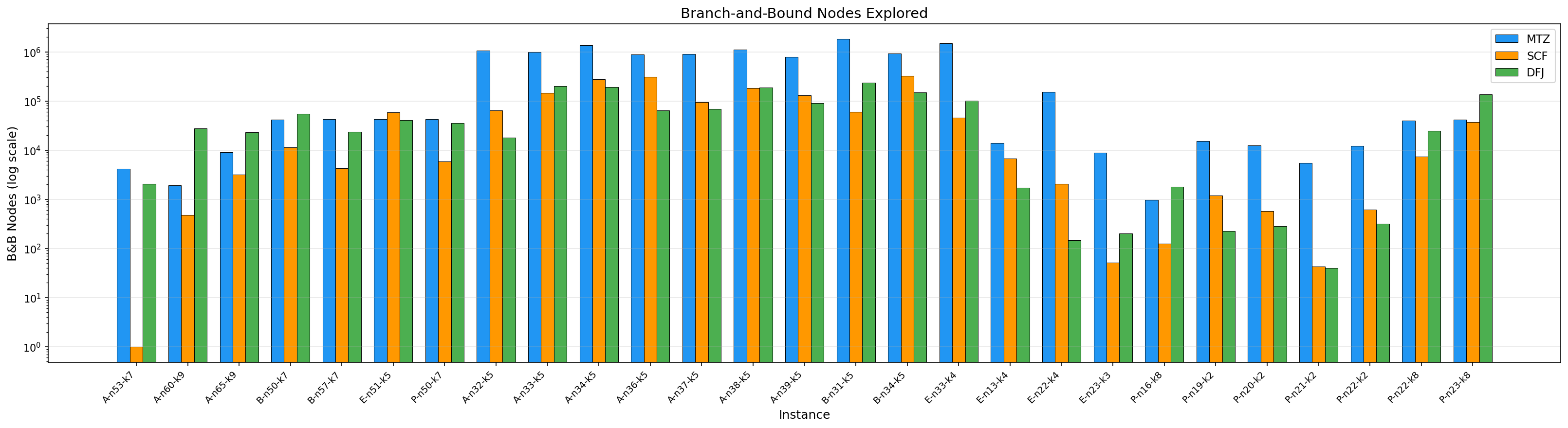
为什么 LP 松弛是关键？

B&B 的效率取决于 LP bound 的质量。从 MTZ (~20%) 到 SCF (~10%) 到 MCF (~6%)，LP gap 逐步缩小，求解速度显著提升。但即便 MCF，LP gap 仍有数个百分点。能否进一步收紧？

回顾理论层级------最强的 SP 模型 LP gap 通常仅 1-3%。我们在 E-n13-k4 上实测 SP LP gap = 9.0%（根节点，无 cuts），远低于 MCF 的 11.0%。对于更复杂的实例，差距更大。

但 SP 模型有指数多个变量（每条可行路线一个），不能直接枚举。解决方案：列生成 （Column Generation），通过迭代求解定价子问题来按需生成有价值的路线。列生成 + 分支定界 = Branch-and-Price（B&P）；再加上切割平面 = Branch-Price-and-Cut（BPC）。这就是下一篇的主题。

完整代码

本文完整代码位于 GitHub 仓库的 vrp-papers/cvrp-mip/ 目录：

mip_models.py：6 种 MIP 模型实现（depot 约束 $\\geq K_{\\min}$ ）
benchmark_runner.py：批量求解 + 结果收集
plot_results.py：生成对比图表

依赖：gurobipy, numpy, vrplib, matplotlib

参考文献

Miller, C. E., Tucker, A. W., & Zemlin, R. A. (1960). Integer programming formulation of traveling salesman problems. Journal of the ACM, 7(4), 326-329.
Gavish, B., & Graves, S. C. (1978). The travelling salesman problem and related problems. Working Paper OR-078-78, MIT.
Dantzig, G. B., Fulkerson, D. R., & Johnson, S. M. (1954). Solution of a large-scale traveling-salesman problem. Journal of the Operations Research Society of America, 2(4), 393-410.
Christofides, N., Mingozzi, A., & Toth, P. (1981). Exact algorithms for the vehicle routing problem, based on spanning tree and shortest path relaxations. Mathematical Programming, 20(1), 255-282.
Laporte, G., Nobert, Y., & Desrochers, M. (1985). Optimal routing under capacity and distance restrictions. Operations Research, 33(5), 1050-1073.
Cornuejols, G., & Harche, F. (1993). Polyhedral study of the capacitated vehicle routing problem. Mathematical Programming, 60, 21-52.
Kara, I., Laporte, G., & Bektas, T. (2004). A note on the lifted Miller-Tucker-Zemlin subtour elimination constraints for the capacitated vehicle routing problem. European Journal of Operational Research, 158(3), 793-795.
Baldacci, R., Hadjiconstantinou, E., & Mingozzi, A. (2004). An exact algorithm for the capacitated vehicle routing problem based on a two-commodity network flow formulation. Operations Research, 52(5), 723-738.
Letchford, A. N., & Salazar-Gonzalez, J.-J. (2006). Projection results for vehicle routing. Mathematical Programming, 105(2-3), 251-274.
Laporte, G. (1992). The vehicle routing problem: An overview of exact and approximate algorithms. European Journal of Operational Research, 59(3), 345-358.
Letchford, A. N., & Salazar-Gonzalez, J.-J. (2015). Stronger multi-commodity flow formulations of the capacitated vehicle routing problem. European Journal of Operational Research, 244(3), 730-738.
Toth, P., & Vigo, D. (Eds.). (2014). Vehicle Routing: Problems, Methods, and Applications (2nd ed.). SIAM.

一起交流

如果你觉得有帮助，欢迎：

📌 订阅本专栏，跟进后续更新
💬 评论区留言，交流你的想法
⭐ 点赞收藏，让更多朋友看到

--- Sebastilan & Claude