摘要
今日学习围绕CFD仿真，涵盖从几何前处理、网格划分、求解计算到后处理的完整流程，并深入探讨了空气动力学中等熵流动公式在边界条件设置中的关键应用。
Abstract
Today's learning revolves around CFD simulation, covering the complete workflow from geometry preprocessing, mesh generation, solution computation to post-processing, and delves into the critical application of isentropic flow formulas from aerodynamics in setting boundary conditions.
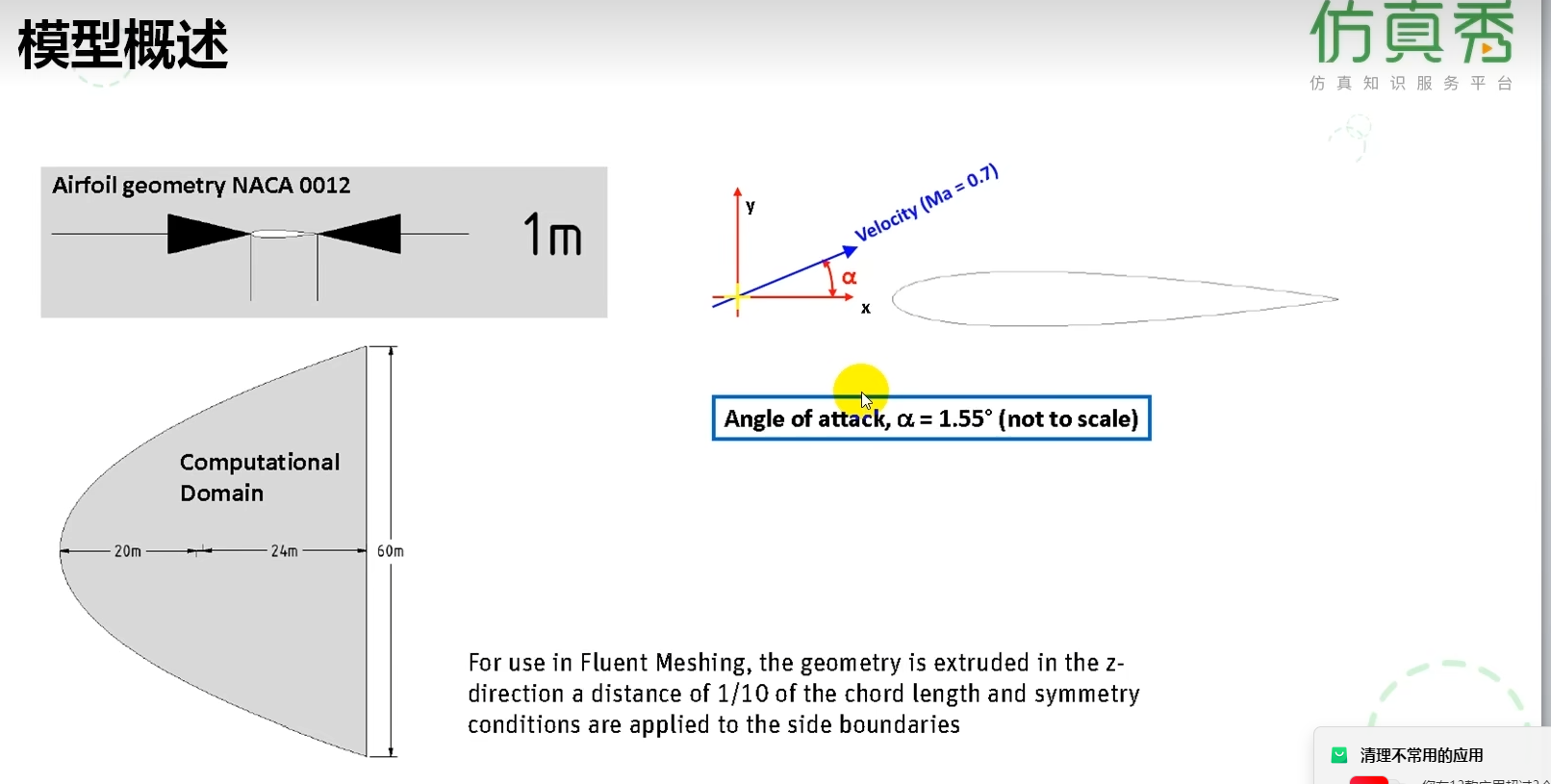
几何与基准模型：采用NACA 0012这一对称翼型作为标准几何，弦长1米，使其结果易于与经典理论和公开实验数据对比验证。
流动条件：来流马赫数0.7，攻角1.55°。这定义了一个典型的高亚音速/跨音速流动场景，翼型表面可能出现局部超音速区及激波，是检验求解器对可压缩流和激波捕捉能力的常用条件。
计算域设置：计算域尺寸远大于翼型（如长度达60倍弦长），旨在确保远场边界（通常设为压力远场或自由流条件）对翼型附近的复杂流动（如激波、分离）干扰最小，符合空气动力学外流场仿真的最佳实践。
模型简化与网格策略：备注说明将在垂直方向（Z向）拉伸1/10弦长并施加对称边界条件。这实质上是将问题简化为二维模拟（使用一层网格单元），并利用对称性来模拟无限展长翼型的流动，能极大降低计算成本，是处理此类典型二维翼型问题的标准方法。
其核心是两组描述可压缩、等熵流动的基本关系式：总压与静压的关系，以及总温与静温的关系。公式中的比热比γ取值为1.4，这特指空气；马赫数M给定为0.7，明确了流动处于高亚音速范围；同时提供了总压Po（101325 Pa，即标准大气压）和总温To（311 K）的具体数值。在实际的CFD仿真设置中，尤其是设置"压力远场"这类边界条件时，软件通常要求输入来流的静压、静温和马赫数。因此，我们需要利用这两个公式，根据已知的总参数（Po, To）和马赫数（M=0.7），反推出对应的静压（P）和静温（T）作为输入值。简而言之，这张图提供了从理论公式到具体工程参数的完整桥梁，是连接流动物理与仿真软件边界条件设定的直接依据。
其核心结构按照仿真流程分为四个主要阶段：
几何处理：使用 SCDM 软件，其技术要点在于导入的几何已经完成了必要的边界命名（如入口、出口、壁面），这为后续的网格划分和边界条件设置奠定了直接基础，是提高前处理效率的关键。
网格划分：采用 Fluent Meshing 的 水密网格工作流。技术要点非常具体且关键：生成 多面体网格 以兼顾精度与计算效率；仅包含流体区域，表明这是一个纯外流场或内部流场的模拟；应用 多区域局部尺寸控制 以在关键区域（如翼型附近）加密网格；并生成 边界层网格 以精确解析近壁面的流动梯度。
求解计算：在 Fluent 求解器中完成。技术要点明确指向一个典型的外流空气动力学仿真：设置可压缩流模型；使用标准的空气材料属性；通过攻角和压力远场边界条件来定义来流状态；监控升力与阻力系数作为核心性能指标。
后处理与验证：同样在 Fluent 中完成，包括生成流场云图进行定性观察，进行定量数据分析，并将仿真结果与实验数据对比以验证计算的准确性，这是闭环工程分析的必要步骤。
今天的知识点主要包括：
一、CFD仿真全流程与项目实践
完整流程包括前处理（使用SCDM进行几何定义与边界命名）、网格划分（采用Fluent Meshing水密工作流生成多面体网格与边界层）、求解计算（在Fluent中设置可压缩流、压力远场边界并监控力系数）以及后处理（结果可视化与实验数据对比）。这完整实践了从几何到报告的标准化工程项目执行。
二、空气动力学理论基础与边界条件设置
重点讲解了等熵流动关系式，即总压/静压与总温/静温随马赫数变化的公式。这些公式是连接理论物理量与CFD软件输入参数的桥梁，用于根据给定的总参数（如Po=101325 Pa, To=311 K）和马赫数（如M=0.7），反推出仿真中必须输入的来流静压和静温，从而正确设置压力远场等边界条件。