极坐标内的2点结构只有1种可能
|---|----|
| 1 | * |
点和中心在一条直线上,可能有两个状态
|---|----|----|
| A | 1 | * |
| | | |
| B | * | 1 |
点1就是在A和B两个状态之间不断的变换,从A到B和从B到A的时间相同为t,初始状态可能为A也可能为B,在t内移动的距离为2r。
让r=5.2917706*10**-11m,
电量是e=-1.602176*10**-19c
真空介电常量ε=8.854187817*10**-12F/m
计算E=m*v*v/2 -1/r
展开1/r得到
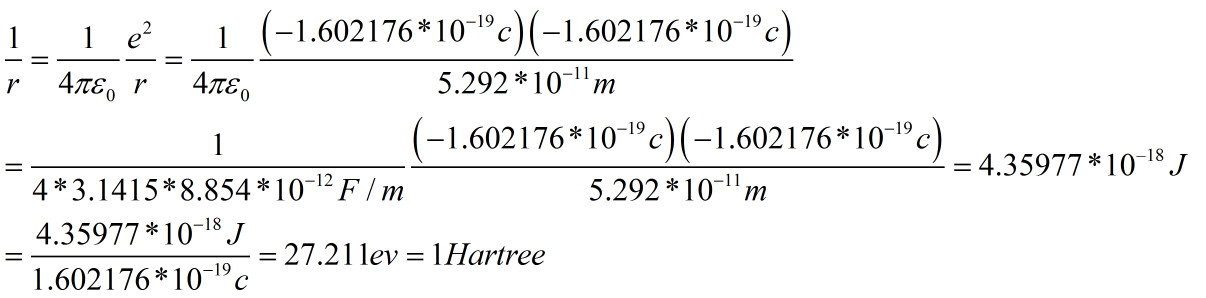
所以当点1距圆心为波尔半径时的动能就是0.5Hartree
在模长和幅角可自由变化的极坐标平面上3点结构有3个
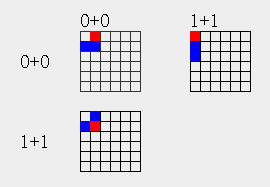
设两个点以0+0|0+0的方式绕核运动,在2*2的范围内可能有8个状态
|---|---|----|----|---|---|---|----|----|
| 0 | | 1 | * | | 4 | | * | 0 |
| | | 1 | 0 | | | | 1 | 1 |
| | | | | | | | | |
| 1 | | 1 | 1 | | 5 | | 1 | 0 |
| | | * | 0 | | | | 1 | * |
| | | | | | | | | |
| 2 | | * | 1 | | 6 | | 0 | * |
| | | 0 | 1 | | | | 1 | 1 |
| | | | | | | | | |
| 3 | | 1 | 1 | | 7 | | 0 | 1 |
| | | 0 | * | | | | * | 1 |
但这里假设
|---|----|
| 2 | 1 |
| | * |
点1相对于核静止,
|---|---|----|---|---|----|---|
| A | 2 | 1 | | B | 1 | 2 |
| | | * | | | * | |
因此只有A,B两个状态,设1到核的距离就是波尔半径,1与2的距离也是波尔半径,计算
E=-mv1*v1/2-mv1*v1/2-2/r1-2/r2 +1/r12
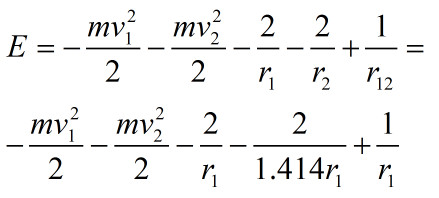
因为r1=波尔半径因此
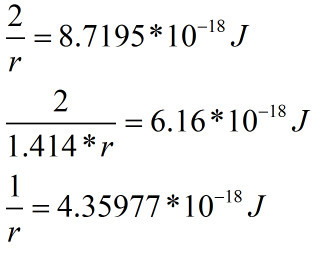
所以得到
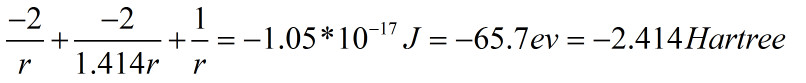
因为1点不动,2点绕1点旋转,半径为波尔半径,因此1的动能是0,2的动能就是-0.5Hartree
E=-0.5-2.415=-2.915Hartree
Python代码
import sympy
a0=sympy.Symbol('a0' )
e=sympy.Symbol('e' )
r=sympy.Symbol('r' )
ε=sympy.Symbol(' ε ' )
# 波尔半径 m
a0=5.2917706*10**-11
# 电量 c
e=-1.602176*10**-19
# 真空介电常量 F/m
ε=8.854187817*10**-12
pi=sympy.pi
f= ( 1/(4*pi*ε))*(2*e*e/a0)
print ( f.evalf() )
#8.71948502594835e-18 J
f1=f/1.414
#6.16653820788426e-18 J
f2=f/2
#4.35974251297417e-18 J
#print ( f1.evalf() )
#print ( f2.evalf() )
f3=-f-f1+f2
print ( f3.evalf() )
#-1.05262807208584e-17 J
print ( f3.evalf()/(e*27.2114) )
#2.41442566857192 Hartree