前言
1. 永磁同步电机
详细的电机的内部构造动画介绍视频:同步磁阻电机原理_哔哩哔哩_bilibili
2. 基础概念
2.1 电枢绕组和励磁绕组
励磁:是指为电机或电器的电磁线圈通入电流,以产生工作所必需的磁场的物理过程及实现该过程所需的整套系统。简单来说,当往一个线圈通入电流,产生磁场的这个过程,可以称为励磁。
不管任何电机,都会包含定子和转子。
常见的直流有刷电机,定子固定在机壳:
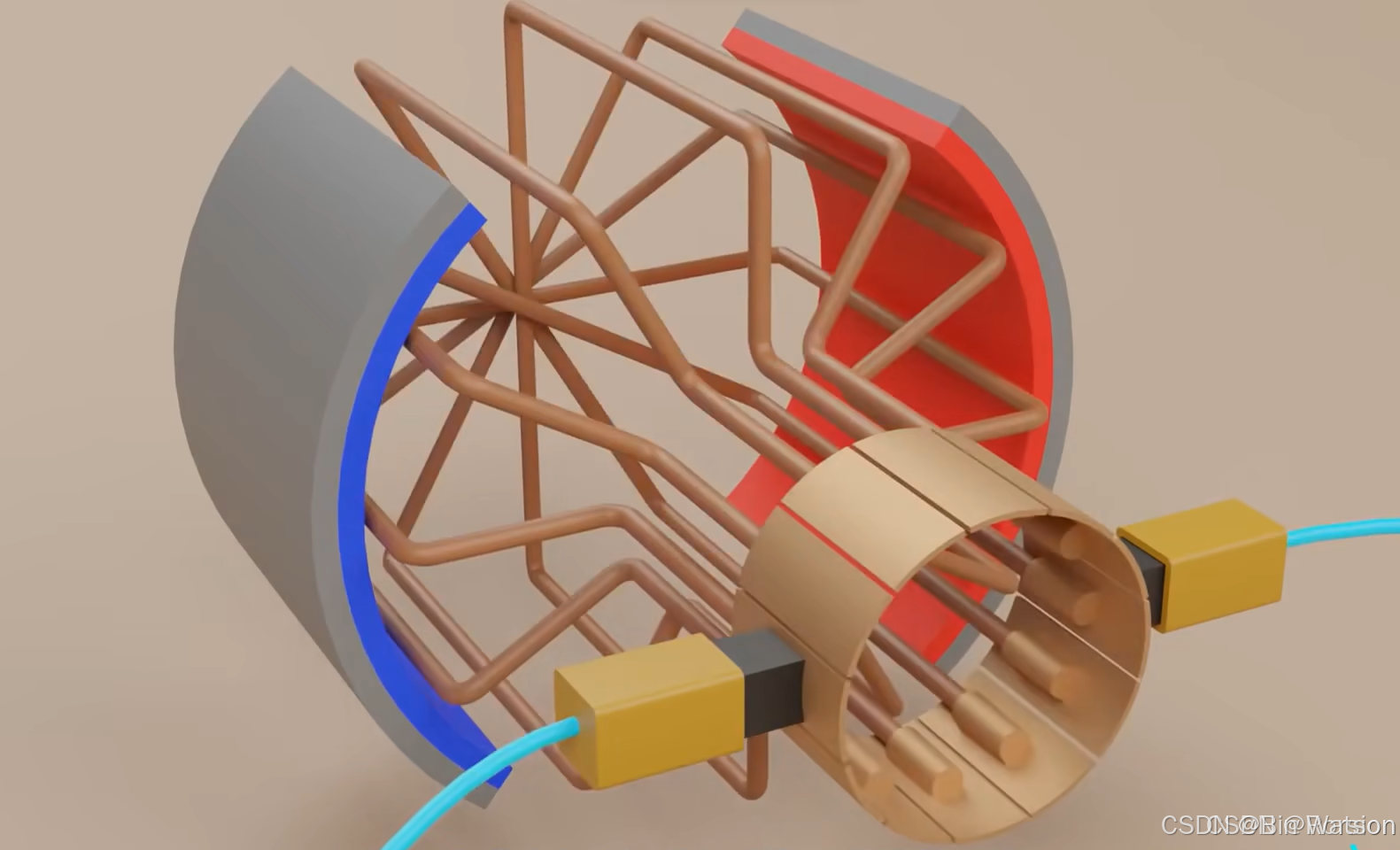
定子通常由永磁体来充当,如果我们把定子改为由直流电驱动从而产生的磁体,那么就这个产生磁体的绕组,可以称为励磁绕组。
而对于通入交变电流产生的磁场的绕组,可以称为电枢绕组。对于直流无刷电机的转子绕组,可以称其为电枢绕组,原因是其本质上流过的也是 AC 电流,只不过这个电流切换是由碳刷帮我们完成的。
对于永磁同步电机,也是如此:
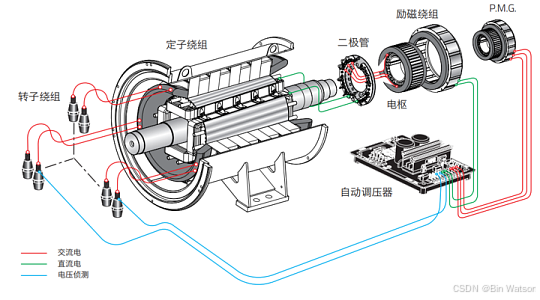
其定子是电枢绕组,通入三相的 AC 电流,形成旋转的磁场;转子一般的励磁绕组,或者直接使用永磁体。
总结一下:
电枢绕组 :通入 AC 电流,与外部系统产生的能量交换。
励磁绕组:通入 DC 电流,产生励磁磁场,充当永磁体的作用。
2.2 机械角度和电角度
机械角度:描述电机转子在物理空间实际转过的角度。
电周期/电角度 :描述电机内部电磁量(电压、电流、磁势)的变化周期,它与磁场的空间分布直接相关。
这是理解电机工作原理的关键。电机内部磁场是按N-S极对周期性分布的。
例如:
- 2极电机 (p=1),转子只有一对磁极(1个N极,1个S极)。
当转子在物理空间(机械角度)上旋转一圈(360°机械角度)时,定子绕组所"经历"的磁场也恰好完成一个完整的变化周期(从N极到S极再回到N极)。因此,此时 360°机械角度 = 360°电角度。 - 4极电机 (p=2) 转子有两对磁极(N-S-N-S交替分布)。
当转子在物理空间上只旋转半圈(180°机械角度)时,定子绕组就已经"经历"了一个完整的磁场周期。因为在这半圈内,磁场方向对绕组来说已经反转了一次。因此,此时 180°机械角度 = 360°电角度。
2.3 自感和互感
电感上的电压(电动势)方程:
V = d ϕ d t = L d i d t V=\frac{d\phi}{dt}=L\frac{di}{dt} V=dtdϕ=Ldtdi
其中 L L L 为电感量, d i d t \frac{di}{dt} dtdi 为电流变化率。
电感(Inductance)是闭合回路的一种属性,即当通过闭合回路的电流改变时,会出现电动势来抵抗电流的改变。如果这种现象出现在自身回路中,那么这种电感称为自感。
互感:如果有两只线圈互相靠近,则其中第一只线圈中电流所产生的磁通有一部分与第二只线圈相环链。 当第一线圈中电流发生变化时,则其与第二只线圈环链的磁通也发生变化,在第二只线圈中产生感应电动势。 这种现象叫做互感现象。
3. 永磁同步电机数学建模
数学建模的目的是为了方便我们能够对电机的进行清晰的描述。例如:我们通过三相电流对电机进行控制,那么我们就希望有一个表达式能够描述,这个三相电流和电机的运动之间的关系。
3.1 自然坐标系建模
从直观感受上,自然趋向于采用自然坐标系来对电机进行建模:
假设三相 PMSM 为理想电机,并且满足下列的条件:
- 忽略电机铁芯的饱和;
- 不计电机中的涡流和磁滞损耗;
- 电机中的电流为对称的三相正弦波电流;
则可以有,自然坐标系下(A-B-C坐标系)的三相电压方程推导如下:
第一步,基于电路理论(基尔霍夫电压定律)和法拉第电磁感应定律。对于永磁同步电机,每相绕组都有电阻、自感和互感,还有永磁体产生的磁链。
在自然坐标系下,三相电压方程可以写为:
{ v a = R s i a + d λ a d t v b = R s i b + d λ b d t v c = R s i c + d λ c d t \begin{cases} v_a = R_s i_a + \frac{d\lambda_a}{dt}\\ v_b = R_s i_b + \frac{d\lambda_b}{dt}\\ v_c = R_s i_c + \frac{d\lambda_c}{dt}\\ \end{cases} ⎩ ⎨ ⎧va=Rsia+dtdλavb=Rsib+dtdλbvc=Rsic+dtdλc
其中, v x v_x vx、 i x i_x ix、 λ x \lambda_x λx 分别为各相的瞬时电压、电流和全磁链, R s R_s Rs 为定子每相电阻。
第二步,建立全磁链的具体表达式。 全磁链是电流和永磁体共同作用的结果,以 A 相为例:
λ a = λ a a + λ a b + λ a c + λ p m , a ( θ e ) \lambda_a = \lambda_{aa} + \lambda_{ab} + \lambda_{ac} + \lambda_{pm,a}(\theta_e)\\ λa=λaa+λab+λac+λpm,a(θe)
- λ a a = L a a i a \lambda_{aa} = L_{aa}i_a λaa=Laaia:A 相自身电流 i a {i_a} ia 产生的、与 A 相绕组交链的磁链(自感磁链)。
- λ a b = M a b i b \lambda_{ab} = M_{ab}i_b λab=Mabib:B 相电流 i b {i_b} ib 产生的、与 A 相绕组交链的磁链(互感磁链)。
- λ a c = M a c i c \lambda_{ac} = M_{ac}i_c λac=Macic:C 相电流 i c {i_c} ic 产生的、与 A 相绕组交链的磁链(互感磁链)。
- λ p m , a \lambda_{pm,a} λpm,a:转子永磁体产生的、与A相绕组交链的磁链(永磁磁链)。
因此,三相的全磁链方程用矩阵形式表示为:
λ a λ b λ c \] = \[ L a a M a b M a c M b a L b b M b c M c a M c b L c c \] \[ i a i b i c \] + \[ λ p m , a λ p m , b λ p m , c \] \\begin{matrix} \\begin{bmatrix} \\lambda_a\\\\ \\lambda_b\\\\ \\lambda_c \\end{bmatrix}= \\begin{bmatrix} L_{aa}\&M_{ab}\&M_{ac}\\\\ M_{ba}\&L_{bb}\&M_{bc}\\\\ M_{ca}\&M_{cb}\&L_{cc} \\end{bmatrix} \\begin{bmatrix} i_a\\\\ i_b\\\\ i_c \\end{bmatrix}+ \\begin{bmatrix} \\lambda_{pm,a}\\\\ \\lambda_{pm,b}\\\\ \\lambda_{pm,c} \\end{bmatrix} \\end{matrix} λaλbλc = LaaMbaMcaMabLbbMcbMacMbcLcc iaibic + λpm,aλpm,bλpm,c 大部分书籍,常常简记为: λ a b c = L a b c i a b c + λ p m , a b c \\lambda_{abc} = L_{abc} i_{abc} + \\lambda_{pm,abc} λabc=Labciabc+λpm,abc **第三步,确定电感矩阵和永磁磁链的具体形式。** 这些参数是转子位置(电角度 θ e \\theta_e θe)的函数,其具体形式由电机结构决定。 * 对于表贴式 PMSM,气隙均匀,可近似认为自感和互感为常数: { L a a = L b b = L c c = L s M a b = M b a = M a c = M c a = M b c = M c b \\begin{cases} L_{aa} = L_{bb} = L_{cc} = L_s\\\\ M_{ab} = M_{ba} = M_{ac} = M_{ca} = M_{bc} = M_{cb} \\end{cases} {Laa=Lbb=Lcc=LsMab=Mba=Mac=Mca=Mbc=Mcb 且通常有 L s \> 0 L_s \\gt 0 Ls\>0, M \< 0 M \\lt 0 M\<0。对于三相对称绕组,在无漏磁的理想情况下, M = − L s 2 M = -\\frac{L_s}{2} M=−2Ls。 首先,确定 L a b c L_{abc} Labc: * 对于内置式PMSM,由于凸极效应( L d ≠ L q L_d \\neq L_q Ld=Lq)电感会随转子位置周期性变化。以 A 相自感为例,其典型表达式为: L a a ( θ e ) = L s 0 + L s 2 c o s ( 2 θ e ) L_aa(\\theta_e) = L_{s0} + L_{s2}cos(2\\theta_e) Laa(θe)=Ls0+Ls2cos(2θe) 互感也有类似形式,例如 M a b ( θ e ) = M 0 + M 2 c o s ( 2 θ e − 2 π 3 ) M_{ab}(\\theta_e) = M_0 + M_2 cos(2\\theta_e - \\frac{2\\pi}{3}) Mab(θe)=M0+M2cos(2θe−32π),电感矩阵中的每个元素都是 θ e \\theta_e θe 的函数。 然后,再确定 λ p m , a b c \\lambda_{pm,abc} λpm,abc: 假设永磁体产生的磁场在气隙中呈正弦分布,则与各相绕组交链的永磁磁链也是 θ e \\theta_e θe: { λ p m , a = λ p m c o s ( θ e ) λ p m , b = λ p m c o s ( θ e − 2 π 3 ) λ p m , c = λ p m c o s ( θ e + 2 π 3 ) \\begin{cases} \\lambda_{pm,a} = \\lambda_{pm}cos(\\theta_e)\\\\ \\lambda_{pm,b} = \\lambda_{pm}cos(\\theta_e - \\frac{2\\pi}{3})\\\\ \\lambda_{pm,c} = \\lambda_{pm}cos(\\theta_e + \\frac{2\\pi}{3})\\\\ \\end{cases} ⎩ ⎨ ⎧λpm,a=λpmcos(θe)λpm,b=λpmcos(θe−32π)λpm,c=λpmcos(θe+32π) 其中 λ p m \\lambda_{pm} λpm 是永磁磁链的幅值。 **最后,得到完整的自然坐标系电压方程** 。将磁链方程代入电压方程,并注意到电感矩阵和永磁磁链是时变的通过( θ e ( t ) θ_e(t) θe(t)),求导时需用乘积法则: v a b c = R s i a b c + d \[ L a b c ( θ e ) i a b c \] d t + d \[ λ p m , a b d ( θ e ) \] d t v_{abc} = R_si_{abc} + \\frac{d\[L_{abc}(\\theta_e)i_{abc}\]}{dt} + \\frac{d\[\\lambda_{pm,abd}(\\theta_e)\]}{dt} vabc=Rsiabc+dtd\[Labc(θe)iabc\]+dtd\[λpm,abd(θe)
展开导数项:
{ d [ L a b c ( θ e ) i a b c ] d t = L a b c ( θ e ) d i a b c d t + d L a b c ( θ e ) d θ e d θ e d t i a b c d [ λ p m , a b d ( θ e ) ] d t = d λ p m , a b c ( θ e ) d θ e d θ e d t \begin{cases} \frac{d[L_{abc}(\theta_e)i_{abc}]}{dt} = L_{abc}(\theta_e)\frac{di_{abc}}{dt} + \frac{dL_{abc}(\theta_e)}{d\theta_e}\frac{d\theta_e}{dt}i_{abc}\\ \frac{d[\lambda_{pm,abd}(\theta_e)]}{dt}=\frac{d\lambda_{pm,abc}(\theta_e)}{d\theta_e}\frac{d\theta_e}{dt} \end{cases} {dtd[Labc(θe)iabc]=Labc(θe)dtdiabc+dθedLabc(θe)dtdθeiabcdtd[λpm,abd(θe)]=dθedλpm,abc(θe)dtdθe
定义电角速度 ω e = d θ e d t \omega_e = \frac{d\theta_e}{dt} ωe=dtdθe,最终电压方程可写为:
v a b c = R s i a b c + L a b c ( θ e ) d i a b c d t + ω e d L a b d ( θ e ) d θ e i a b c + ω e d λ p m , a b c ( θ e ) d θ e v_{abc} = R_si_{abc} + L_{abc}(\theta_e)\frac{di_{abc}}{dt} + \omega_e\frac{dL_{abd}(\theta_e)}{d\theta_e}i_{abc} + \omega_e\frac{d\lambda_{pm,abc}(\theta_e)}{d\theta_e} vabc=Rsiabc+Labc(θe)dtdiabc+ωedθedLabd(θe)iabc+ωedθedλpm,abc(θe)
这个方程是 PMSM 在自然坐标系下最原始、最完整的数学模型。然而,这个模型是时变的、强耦合的、非线性的(因为电感矩阵和反电势是 θ e θ_e θe 的函数),不便于直接用于分析和控制。
是否能够简化建模呢?
答案是肯定的,这就是电机上采用 d-q 轴(坐标系)建模的原因。
3.2 d-q 旋转坐标系建模
将自然坐标系建模中的磁链方程和电压方程,通过 Clarke 变换和 Park 变换后就可以得到 d-q 坐标系下的电压方程和磁链方程。
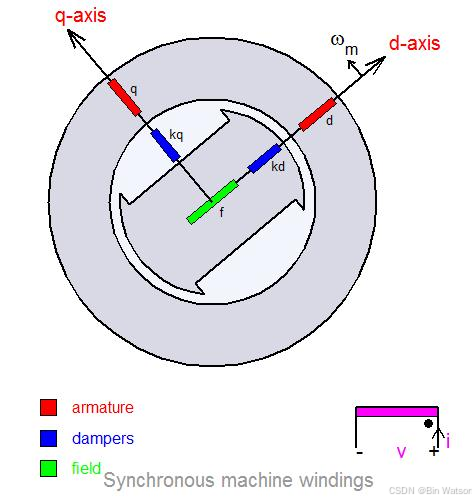
自然坐标系:
-
电压方程(简记形式):
v a b c = R s i a b c + d λ a b c d t v_{abc} = R_si_{abc} + \frac{d\lambda_{abc}}{dt} vabc=Rsiabc+dtdλabc -
磁链方程(简记形式):
λ a b c = L a b c i a b c + λ p m , a b c \lambda_{abc} = L_{abc} i_{abc} + \lambda_{pm,abc} λabc=Labciabc+λpm,abc
d-q 坐标系:
- 电压方程:
{ u d = R s i d + d λ d d t − ω e λ q u q = R s i q + d λ q d t + ω e λ d \begin{cases} u_d = R_si_d+\frac{d\lambda_d}{dt}-\omega_e\lambda_q\\ u_q = R_si_q+\frac{d\lambda_q}{dt}+\omega_e\lambda_d\\ \end{cases} {ud=Rsid+dtdλd−ωeλquq=Rsiq+dtdλq+ωeλd - 磁链方程:
{ λ d = L d i d + λ p m λ q = L q i q \begin{cases} \lambda_d = L_di_d + \lambda_{pm}\\ \lambda_q = L_qi_q \end{cases} {λd=Ldid+λpmλq=Lqiq
这里 L d L_d Ld、 L q L_q Lq为直轴和交轴电感, λ p m \lambda_{pm} λpm 为永磁体磁链幅值, ω e = d θ e / d t \omega_e = d\theta_e/dt ωe=dθe/dt 为电角速度。
合并得到最终 d-q 坐标系电压方程:
{ u d = R s i d + L d d i d d t − ω e L q i q u q = R s i q + L q d i q d t + ω e ( L d i d + λ p m ) \begin{cases} u_d = R_si_d+L_d\frac{di_d}{dt}-\omega_eL_qi_q\\ u_q = R_si_q+L_q\frac{di_q}{dt}+\omega_e(L_di_d + \lambda_{pm})\\ \end{cases} {ud=Rsid+Lddtdid−ωeLqiquq=Rsiq+Lqdtdiq+ωe(Ldid+λpm)
3.3 电磁转矩方程
对于三相永磁同步电机,定子侧的瞬时电功率为三相电压与电流乘积之和:
P a b c = v a i a + v b i b + v c i c P_{abc} = v_ai_a+v_bi_b+v_ci_c Pabc=vaia+vbib+vcic
其中, v a v_a va、 v b v_b vb、 v c v_c vc、 i a i_a ia、 i b i_b ib、 i c i_c ic 分别为三相瞬时电压和电流。
同理,可以采用 Clarke 和 Park 变换成 d-q 坐标系下功率表达式:
P i n = v d i d + v q i q P_{in} = v_di_d + v_qi_q Pin=vdid+vqiq
将 d-q 坐标系的电压方程代入该式子中,可以得到电机的功率表达式:
P i n = [ ( R s i d + d λ d d t ) i d + ( R s i q + d λ q d t + ω e λ d ) i q ] = R s ( i d 2 + i q 2 ) + ( i d d λ d d t + i q d λ q d t ) + ω e ( λ d i q − λ q i d ) \begin{aligned} P_{in} &= [(R_si_d+\frac{d\lambda_d}{dt})i_d+(R_si_q+\frac{d\lambda_q}{dt}+\omega_e\lambda_d)i_q]\\ &=R_s(i^2_d+i^2_q) + (i_d\frac{d\lambda_d}{dt}+i_q\frac{d\lambda_q}{dt})+\omega_e(\lambda_di_q-\lambda_qi_d) \end{aligned} Pin=[(Rsid+dtdλd)id+(Rsiq+dtdλq+ωeλd)iq]=Rs(id2+iq2)+(iddtdλd+iqdtdλq)+ωe(λdiq−λqid)
其中:
- 第一项: R s ( i d 2 + i q 2 ) R_s(i^2_d+i^2_q) Rs(id2+iq2) 是定子绕组的铜耗。
- 第二项: ( i d d λ d d t + i q d λ q d t ) (i_d\frac{d\lambda_d}{dt}+i_q\frac{d\lambda_q}{dt}) (iddtdλd+iqdtdλq)是磁场储能的变化率(即变压器电动势对应的功率)。
- 第三项: ω e ( λ d i q − λ q i d ) \omega_e(\lambda_di_q-\lambda_qi_d) ωe(λdiq−λqid)是由于转子旋转引起的运动电动势对应的功率 ,这部分功率代表了电能与机械能之间的转换,即电磁功率 P e m P_{em} Pem。
因此,可以得到电功率:
P e m = ω e ( λ d i q − λ q i d ) P_{em} = \omega_e(\lambda_di_q-\lambda_qi_d) Pem=ωe(λdiq−λqid)
根据机电能量转换原理,电磁功率应等于电磁转矩 T e T_e Te乘以机械角速度 ω m \omega_m ωm:
P e m = T e × ω m P_{em} = T_e \times \omega_m Pem=Te×ωm
由于机械角度、电角角度和电机的极对数有: ω e = p ω m \omega_e = p\omega_m ωe=pωm 的关系,代入上式,最终可得:
T e = p ( λ d i q − λ q i d ) T_e = p(\lambda_diq-\lambda_qid) Te=p(λdiq−λqid)
将磁链方程 λ d = L d i d + λ p m \lambda_d = L_di_d + \lambda_{pm} λd=Ldid+λpm, λ q = L q i q \lambda_q = L_qi_q λq=Lqiq 代入上式,得到形式永磁同步电机电磁转矩的最终表达式 (这里加上了 3/2 做了等幅值处理,不理解这块无所谓,从理解公式的角度上并不重要):
T e = 3 2 p [ λ p m i q + ( L d − L q ) i d i q ] T_e = \frac{3}{2}p[\lambda_{pm}i_q + (L_d - L_q)i_di_q] Te=23p[λpmiq+(Ld−Lq)idiq]
其中:
-
永磁转矩项 : 3 2 p λ p m i q \frac{3}{2}p\lambda_{pm}i_q 23pλpmiq
由永磁磁场与电枢反应磁场(q轴电流产生)相互作用产生,与 i q i_q iq 成正比,是表贴式永磁电机( L d = L q L_d = L_q Ld=Lq)的主要转矩来源。
-
磁阻转矩项 : 3 2 p ( L d − L q ) i d i q \frac{3}{2}p(L_d - L_q)i_di_q 23p(Ld−Lq)idiq
由于直轴与交轴磁路不对称( L d ≠ L q L_d \neq L_q Ld=Lq)引起,是内置式永磁电机 (通常 L d < L q L_d \lt L_q Ld<Lq)的重要转矩分量。通过合理控制 i d i_d id(通常为负值),可以充分利用磁阻转矩,提高转矩输出和效率。
4. 关于 i q i_q iq 和 i d i_d id 更进一步理解
逆变器能输出的最大相电压幅值 U m a x U_{max} Umax 受直流母线电压限制,在 d-q 坐标系下,电压需要满足:
u d 2 + u q 2 ≤ U m a x 2 u^2_d+u^2_q \le U^2_{max} ud2+uq2≤Umax2
根据前面推导的 d-q 坐标系下的电压方程:
{ u d = R s i d + L d d i d d t − ω e L q i q u q = R s i q + L q d i q d t + ω e ( L d i d + λ p m ) \begin{cases} u_d = R_si_d+L_d\frac{di_d}{dt}-\omega_eL_qi_q\\ u_q = R_si_q+L_q\frac{di_q}{dt}+\omega_e(L_di_d + \lambda_{pm})\\ \end{cases} {ud=Rsid+Lddtdid−ωeLqiquq=Rsiq+Lqdtdiq+ωe(Ldid+λpm)
如果忽略电感和电阻的消耗,只看电角速度 ω e \omega_e ωe 的影响,则有电压极限椭圆方程:
( L q i q ) 2 + ( L d i d + λ p m ) 2 ≤ ( U m a x ω e ) 2 (L_qi_q)^2 + (L_di_d + \lambda_{pm})^2 \le (\frac{U_{max}}{\omega_e})^2 (Lqiq)2+(Ldid+λpm)2≤(ωeUmax)2
观察公式,可以得到:
- 当电机转速 ω e \omega_e ωe 升高时,不等式右边 ( U m a x ω e ) 2 (\frac{U_{max}}{\omega_e})^2 (ωeUmax)2 急剧缩小,意味着电流矢量 ( i q , i d ) (i_q, i_d) (iq,id)被限制在一个越来越小的椭圆内。
- 永磁体产生的磁链 λ p m \lambda_{pm} λpm 是固定的,它会在 d 轴方向产生一个感生反电势 ω e λ p m \omega_e \lambda_{pm} ωeλpm ,这个反电势会"吃掉"大部分可用的电压额度。
- 为了在高速下仍能让电流进入椭圆内(从而还能输出 i q i_q iq 产生转矩),必须减小方程中 ( L d i d + λ p m ) (L_di_d + \lambda_{pm}) (Ldid+λpm) 这一项
通过注入负的 i d i_d id,可以抵消一部分 λ p m \lambda_{pm} λpm,从而减小合成磁链,降低反电势。这就像给永磁体这个"固定磁场源"加上了一个反向的"电磁场"来削弱它。
因此,在实际的 FOC 控制中:
- 控制 i q i_q iq 来实现转矩/转速控制 ,外环(速度环或转矩环)的输出,可以直接作为 i q i_q iq 的指令值。
- 在基速以下,通常设置 i d = 0 i_d = 0 id=0(或为优化效率设一个小的负值,即 MTPA 控制)。接近或超过基速时:就需要启用弱磁控制器,它监测电压利用率 U u t i l = u d 2 + u q 2 U m a x U_{util} = \frac{\sqrt{u^2_d+u^2_q}}{U_{max}} Uutil=Umaxud2+uq2 ,当 U u t i l U_{util} Uutil 接近等于 1 时,弱磁控制器自动计算并给出一个负的 i d i_d id 指令,以削弱磁场,防止电压饱和,保证 i q i_q iq 指令还能被执行。
关于 i d i_d id 和弱磁的一些更详细的介绍可以参考 永磁同步电机矢量控制(FOC)---弱磁控制(超前角弱磁)
5. 小结
本篇可能有许多错误和不足,欢迎大家讨论指正。此外,本人刚开始学习电机驱动,很多理论理解还比较肤浅,本篇参考了许多前辈的笔记,此外借助了 AI 辅助理解说明了一些内容。
我感觉,这其一比较难以理解的是为何要建立 d-q 轴作为电机的建模坐标系,相信对比了自然坐标系的建模,大概能够领悟其中的缘由。其二是 i q i_q iq 和 i d i_d id 的作用,借助力矩方程,我们直观看到它们对力矩的影响,以及电机的转速对整个系统运行的动态影响,这可能涉及到高速电机的一些优化策略,如 MTPA 控制等。