两个数组的动态规划

• 最长公共子序列
• • 题目描述
  • 递归
  • 记忆化
  • 动态规划
  • 空间优化
• 不相交的线
• • 题目描述
  • 算法原理和实现
• 不同的子序列
• • 题目描述
  • 算法原理和实现
• 通配符匹配
• • 题目描述
  • 记忆化搜索
  • 动态规划
• 正则表达式匹配
• • 题目描述
  • 算法原理和实现
• 交错字符串
• • 题目描述
  • 算法原理和实现
• 两个字符串的最小ASCII删除和
• • 题目描述
  • 算法原理和实现
• 最长重复子数组
• • 题目描述
  • 算法原理和实现

最长公共子序列

题目描述

最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例 1：

输入：text1 = "abcde", text2 = "ace"

输出：3

解释：最长公共子序列是 "ace" ，它的长度为 3 。

示例 2：

输入：text1 = "abc", text2 = "abc"

输出：3

解释：最长公共子序列是 "abc" ，它的长度为 3 。

示例 3：

输入：text1 = "abc", text2 = "def"

输出：0

解释：两个字符串没有公共子序列，返回 0 。

提示：

• 1 <= text1.length, text2.length <= 1000
• text1 和 text2 仅由小写英文字符组成。

递归

这题实际上和最长回文子序列没什么两样，我们从递归出发推导最优的动态规划。

首先我们对于两个字符串，我们只判断他的首元素是否相等，如果相等：

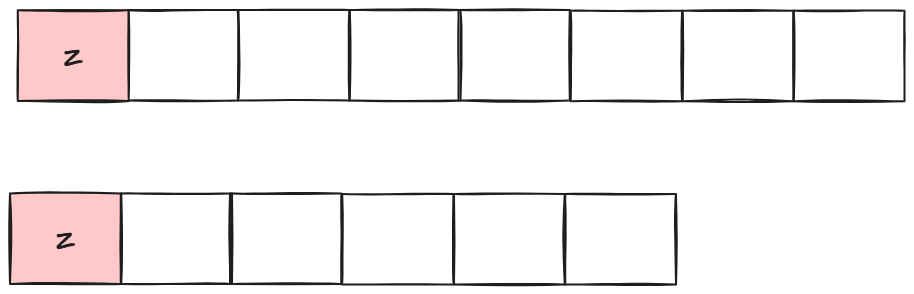
不难发现，我们选取z作为两者的公共子序列开头是不会影响任何后续选取，为最优情况。

所以两个字符串最长公共子序列长度，变成了1+去掉首元素部分的最长公共子序列长度，然后继续比较首元素。

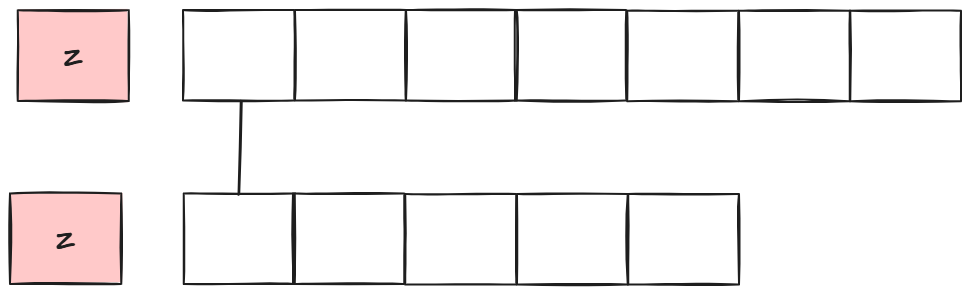
接下来是第二种情况：

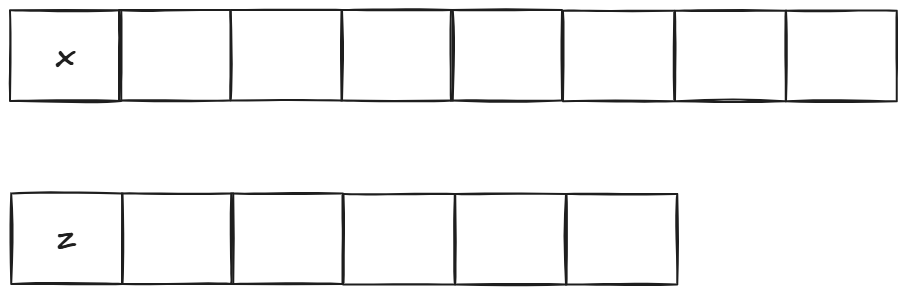
首元素不相等，那么他们的最长公共子序列有三种情况：

1. x开头
2. z开头
3. 非x非z开头

首先是x开头，那么下面字符串的首元素已经不再影响后续公共子串选取可以去掉了：

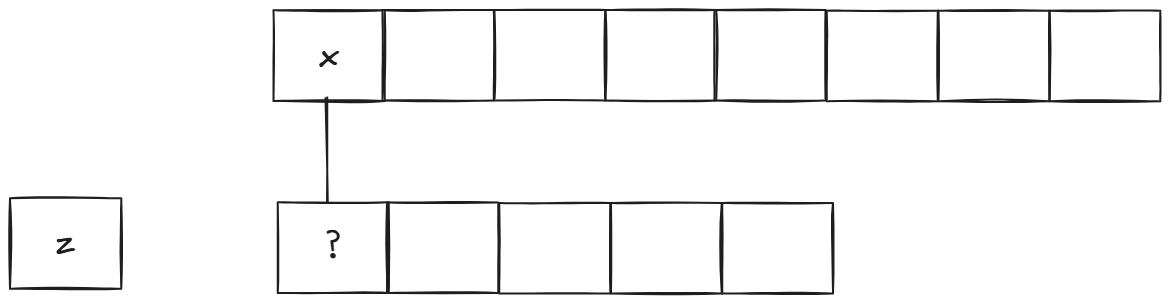
现在变成了这两个字符串的最长公共子序列。

第二种情况是z开头，同理上面字符串首元素可以去掉：

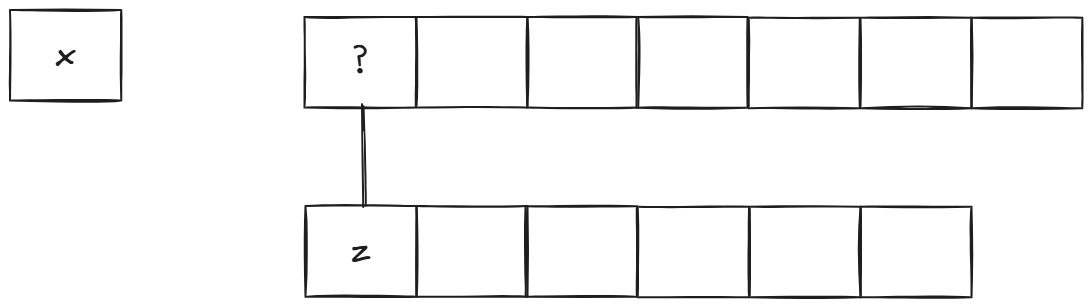
最后是第三种情况，两个首元素都不影响最终结果可以去掉：

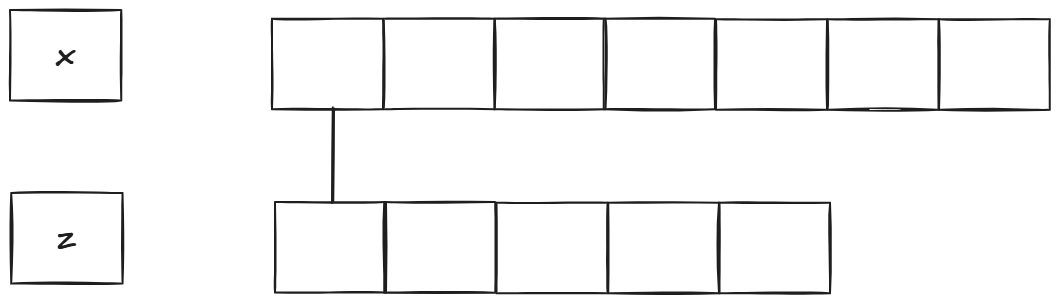
我们用递归的方式实现：

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int n=text1.size(),m=text2.size();
        if(!n||!m)return 0;
        if(text1[0]==text2[0])
            return longestCommonSubsequence(text1.substr(1),text2.substr(1))+1;
        else
            return max(longestCommonSubsequence(text1.substr(1),text2),
            longestCommonSubsequence(text1,text2.substr(1)));
    }
};

记忆化

直接递归搜索会导致叶子部分重复搜索指数次，导致超时。

所以我们考虑记录第一次搜索后的结果，后续再次搜索直接返回即可：

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int n=text1.size(),m=text2.size();
        vector<vector<int>>hash(n,vector<int>(m,-1));
        function<int(int,int)>dfs=[&](int i,int j){
            if(i==n||j==m)return 0;
            if(hash[i][j]<0){
                if(text1[i]==text2[j]){
                    hash[i][j]=1+dfs(i+1,j+1);
                }else{
                    hash[i][j]=max(dfs(i,j+1),dfs(i+1,j));
                }
            }
            return hash[i][j];
        };
        return dfs(0,0);
    }
};

时间复杂度O(mn)，空间复杂度O(mn).

动态规划

其实刚才我们已经将动态规划都推导出来了。

我们定义dp[i][j]为text1以i为起点，text2以j为起点二者的子串的最长公共子序列长度。

那么dp[i][j]依赖于dp[i+1][j+1]、dp[i+1][j]、dp[i][j+1]

因此我们从右下角开始填表。

此外当dp在最后一行和最后一列时，有越界风险，我们大可以多开一行一列的空间来避免越界和初始化，这也是动态规划常用技巧。

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int n=text1.size(),m=text2.size();
        vector<vector<int>>dp(n+1,vector<int>(m+1));
        for(int i=n-1;i>=0;--i){
            for(int j=m-1;j>=0;--j){
                if(text1[i]==text2[j]){
                    dp[i][j]=1+dp[i+1][j+1];
                }else{
                    dp[i][j]=max(dp[i+1][j],dp[i][j+1]);
                }
            }
        }
        return dp[0][0];
    }
};

时间复杂度O(mn)，空间复杂度O(mn)

空间优化

注意到我们每次更新只需要下一行的状态，因此可以空间压缩成一行：

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int n=text1.size(),m=text2.size(),cur,prev;
        if(n<m){
            swap(n,m);
            swap(text1,text2);
        }
        vector<int>dp(m+1);
        for(int i=n-1;i>=0;--i){
            prev=0;
            for(int j=m-1;j>=0;--j){
                cur=dp[j];
                if(text1[i]==text2[j]){
                    dp[j]=1+prev;
                }else{
                    dp[j]=max(dp[j],dp[j+1]);
                }
                prev=cur;
            }
        }
        return dp[0];
    }
};

时间复杂度O(mn)，空间复杂度O(min(m,n))。

实际上数据有范围的话我们还可以进一步优化：

class Solution {
public:
    static int dp[1001];
    int longestCommonSubsequence(string text1, string text2) {
        int n=text1.size(),m=text2.size(),cur,prev;
        memset(dp,0,sizeof(int)*(m+1));
        for(int i=n-1;i>=0;--i){
            prev=0;
            for(int j=m-1;j>=0;--j){
                cur=dp[j];
                if(text1[i]==text2[j]){
                    dp[j]=1+prev;
                }else{
                    dp[j]=max(dp[j],dp[j+1]);
                }
                prev=cur;
            }
        }
        return dp[0];
    }
};
int Solution::dp[1001]{0};

不相交的线

题目描述

不相交的线

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足：

nums1[i] == nums2[j]

且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

示例 1：

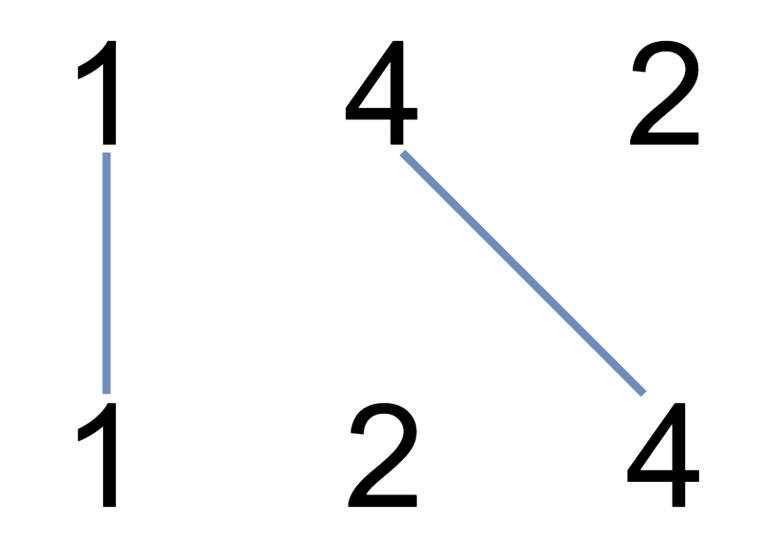
输入：nums1 = [1,4,2], nums2 = [1,2,4]

输出：2

解释：可以画出两条不交叉的线，如上图所示。

但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

示例 2：

输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]

输出：3

示例 3：

输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]

输出：2

提示：

• 1 <= nums1.length, nums2.length <= 500
• 1 <= nums1[i], nums2[j] <= 2000

算法原理和实现

我的论文创新点be like：将最长公共子序列包装成不相交的线。

这两题就是一样的解法，这里不多做赘述：

class Solution {
public:
    static int dp[501];
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        int n=nums1.size(),m=nums2.size(),cur,prev;
        memset(dp,0,sizeof(int)*(m+1));
        for(int i=n-1;i>=0;--i){
            prev=0;
            for(int j=m-1;j>=0;--j){
                cur=dp[j];
                if(nums1[i]==nums2[j]){
                    dp[j]=prev+1;
                }else{
                    dp[j]=max(cur,dp[j+1]);
                }
                prev=cur;
            }
        }
        return dp[0];
    }
};
int Solution::dp[501]{0};

时间复杂度O(mn)，空间复杂度O(n)

不同的子序列

题目描述

不同的子序列

给你两个字符串 s 和 t ，统计并返回在 s 的 子序列 中 t 出现的个数。

测试用例保证结果在 32 位有符号整数范围内。

示例 1：

输入：s = "rabbbit", t = "rabbit"

输出：3

解释：

如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。

rabbbit

rabbbit

rabbbit

示例 2：

输入：s = "babgbag", t = "bag"

输出：5

解释：

如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。

babgbag

babgbag

babgbag

babgbag

babgbag

提示：

• 1 <= s.length, t.length <= 1000
• s 和 t 由英文字母组成

算法原理和实现

老实说这题和上面两题没多少区别,不过我已经厌倦了从右下角开始填表,我决定这次从左上角开始填表.

dp[i][j]表示s以i为结尾的子序列中有t以j为结尾的子串的数目.

那么s中[0,i]的子序列分两种情况:

1. 以i为结尾,我们就要判断s[i]是否与t[j]相等,如果相等dp[i][j]+=dp[i-1][j-1]
2. 不以i为结尾,那直接去掉即可dp[i][j]+=dp[i-1][j]

具体实现:

class Solution {
public:
    int numDistinct(string s, string t) {
        int n=s.size(),m=t.size();
        if(n<m)return 0;
        vector<vector<unsigned long long>>dp(n+1,vector<unsigned long long>(m+1));
        for(int i=0;i<=n;++i)dp[i][0]=1;
        for(int i=1;i<=n;++i){
            for(int j=1;j<=m;++j){
                dp[i][j]=dp[i-1][j];
                if(s[i-1]==t[j-1])
                    dp[i][j]+=dp[i-1][j-1];
            }
        }
        return dp[n][m];
    }
};

时间复杂度和空间复杂度都是O(mn).

这里官解应该是出了点问题,我们要用无符号长长整型才不会溢出.

同理我们可以进行空间优化:

class Solution {
public:
    int numDistinct(string s, string t) {
        int n=s.size(),m=t.size(),cur,prev;
        if(n<m)return 0;
        vector<unsigned long long>dp(m);
        for(int i=0;i<n;++i){
            prev=1;
            for(int j=0;j<m;++j){
                cur=dp[j];
                if(s[i]==t[j])
                    dp[j]+=prev;
                prev=cur;
            }
        }
        return dp[m-1];
    }
};

时间复杂度O(mn),空间复杂度O(m).

通配符匹配

题目描述

通配符匹配

给你一个输入字符串 (s) 和一个字符模式 § ，请你实现一个支持 '?' 和 '' 匹配规则的通配符匹配：
'?' 可以匹配任何单个字符。
' ' 可以匹配任意字符序列（包括空字符序列）。

判定匹配成功的充要条件是：字符模式必须能够 完全匹配 输入字符串（而不是部分匹配）。

示例 1：

输入：s = "aa", p = "a"

输出：false

解释："a" 无法匹配 "aa" 整个字符串。

示例 2：

输入：s = "aa", p = "*"

输出：true

解释：'*' 可以匹配任意字符串。

示例 3：

输入：s = "cb", p = "?a"

输出：false

解释：'?' 可以匹配 'c', 但第二个 'a' 无法匹配 'b'。

提示：

• 0 <= s.length, p.length <= 2000
• s 仅由小写英文字母组成
• p 仅由小写英文字母、'?' 或 '*' 组成

记忆化搜索

这题的难点在于'*'字符的匹配.

我们考虑两字符串的最后一个元素是否相等.

1. 如果是两个普通字符且不相等:
   
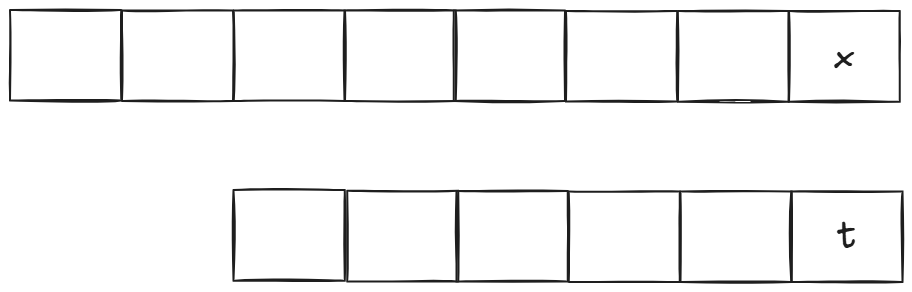
   那我们知道这两个字符串一定不相等.
2. 如果是两个普通字符且相等或者模式串最后一个字符是'?':
   
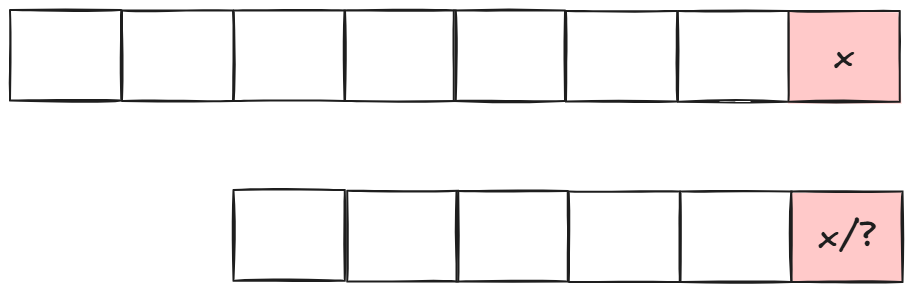
   那这两个字符就不会影响最终结果,可以舍去,我们判断前面字符是否相等即可:
   
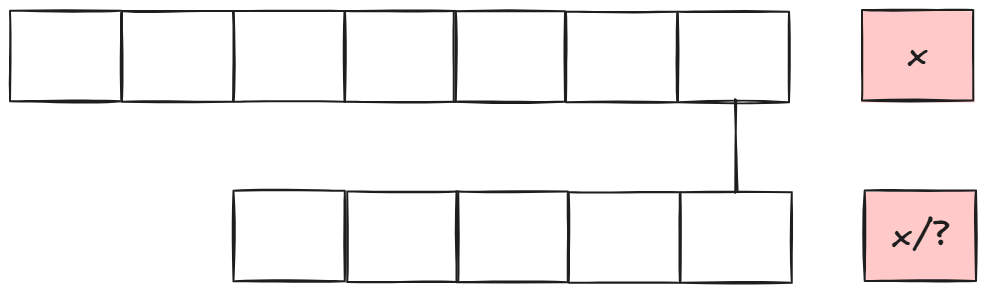
3. 如果模式串最后一个字符是'*',那么'*'可以匹配任意字符:
   
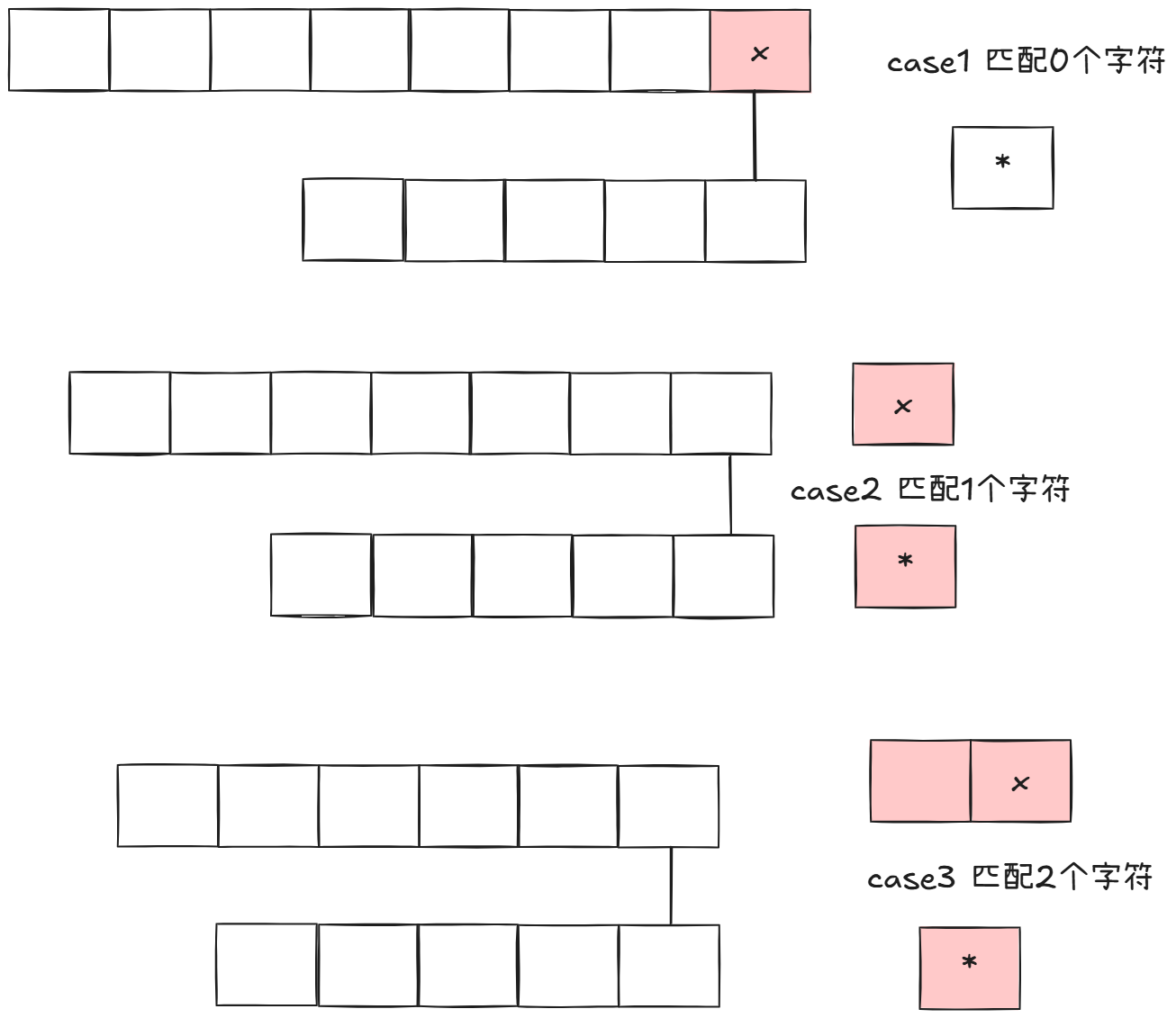
   case1我们只需要将模式串的星号去掉即可,case 2则是两个字符串的末尾元素.我们再看case3 原串去掉两个末尾字符,后两种情况可以合并,具体怎么做呢?
   我们只需要舍弃原串字符而不舍弃'*'即可:
   

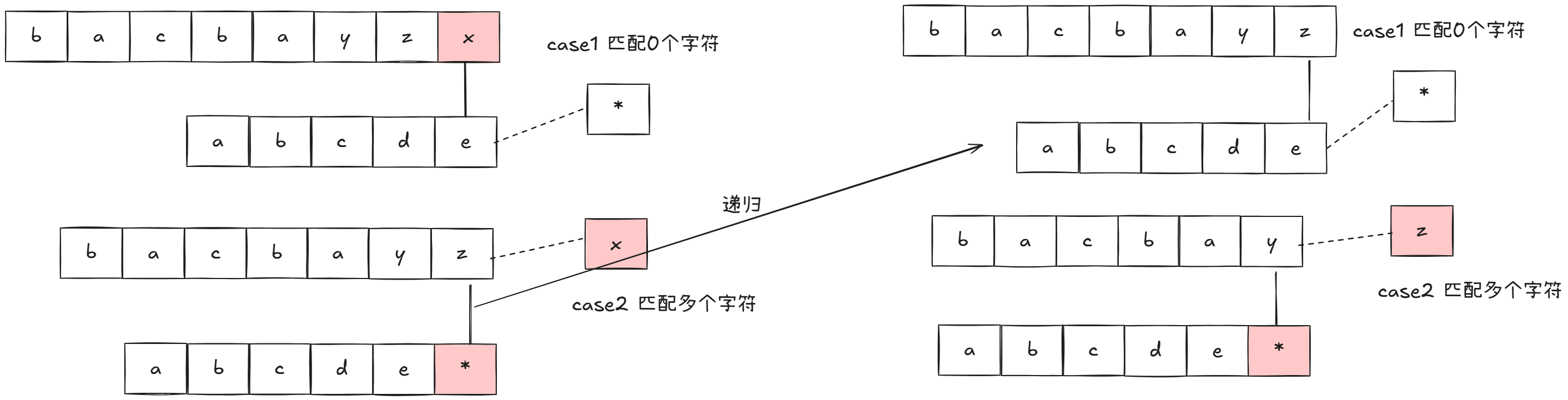
可以看到我们case2递归匹配剩余字符后,如果直接走case1相当于'*'匹配一个字符,如果走case2再走case1,相当于'*'匹配两个字符...

此外我们可以用一个哈希表记录搜索过的结果:

class Solution {
public:
    bool isMatch(string s, string p) {
        int n=s.size(),m=p.size();
        vector<vector<int>>hash(n,vector<int>(m));
        function<bool(int, int)> dfs = [&](int i, int j) {
            if(i<0){
                for(int k=j;k>=0;--k){
                    if(p[k]!='*')return false;
                }
                return true;
            }else if(j<0)return false;

            if(!hash[i][j]){
                bool tmp;
                hash[i][j]=1;
                if(p[j]=='?')tmp=dfs(i-1,j-1);
                else if(p[j]=='*')tmp=dfs(i-1,j)||dfs(i,j-1);
                else if(p[j]==s[i])tmp=dfs(i-1,j-1);
                else tmp=false;
                hash[i][j]+=tmp;
            }

            if(hash[i][j]==2)return true;
            else return false;
        };
        return dfs(n-1,m-1);
    }
};

时间复杂度O(mn),空间复杂度O(mn)

动态规划

根据记忆化搜索的分析.我们定义状态表示为:

dp[i][j]:s以i结尾的前缀和p以j为结尾的前缀能否匹配.

因此我们从左上角开始填表.

• 初始化:
  s的前缀为空串时,p的前缀必须全是'*'才能匹配.
  s和p的前缀都是空串时,匹配.

具体实现:

class Solution {
public:
    bool isMatch(string s, string p) {
        int n=s.size(),m=p.size();
        vector<vector<bool>>dp(n+1,vector<bool>(m+1));
        //j=0时p的空串
        dp[0][0]=true;
        for(int j=0;j<m;++j){
            if(p[j]!='*')break;
            dp[0][j+1]=true;
        }
        for(int i=1;i<=n;++i){
            for(int j=1;j<=m;++j){
                if(p[j-1]=='?')dp[i][j]=dp[i-1][j-1];
                else if(p[j-1]=='*')dp[i][j]=dp[i-1][j]||dp[i][j-1];
                else if(s[i-1]==p[j-1])dp[i][j]=dp[i-1][j-1];
                //else false
            }
        }
        return dp[n][m];
    }
};

时间复杂度O(mn),空间复杂度O(mn)

同样的我们只依赖属于上一行的元素,因此可以进行空间优化:

class Solution {
public:
    bool isMatch(string s, string p) {
        int m=s.size(),n=p.size();
        if(!m&&!n)return true;
        bool cur,prev;
        vector<bool>dp(n+1);
        //j=0时p的空串
        prev=true;
        for(int j=0;j<n;++j){
            if(p[j]!='*')break;
            dp[j+1]=true;
        }
        for(int i=1;i<=m;++i){
            if(i>1)prev=false;
            for(int j=1;j<=n;++j){
                cur=dp[j];
                if(p[j-1]=='?')dp[j]=prev;
                else if(p[j-1]=='*')dp[j]=cur||dp[j-1];
                else if(s[i-1]==p[j-1])dp[j]=prev;
                else dp[j]=false;
                prev=cur;
            }
        }
        return dp[n];
    }
};

时间复杂度O(mn),空间复杂度O(n)

正则表达式匹配

题目描述

正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符

'*' 匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖 整个 字符串 s 的，而不是部分字符串。

示例 1：

输入：s = "aa", p = "a"

输出：false

解释："a" 无法匹配 "aa" 整个字符串。

示例 2:

输入：s = "aa", p = "a*"

输出：true

解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3：

输入：s = "ab", p = ".*"

输出：true

解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

提示：

• 1 <= s.length <= 20
• 1 <= p.length <= 20
• s 只包含从 a-z 的小写字母。
• p 只包含从 a-z 的小写字母，以及字符 . 和 *。
• 保证每次出现字符 * 时，前面都匹配到有效的字符

算法原理和实现

这题和上一题本质没有区别.无非就是'*'要和前一个字符联合使用,并且'*'不再是随意匹配,所以模式串末尾是'*'分两种情况:

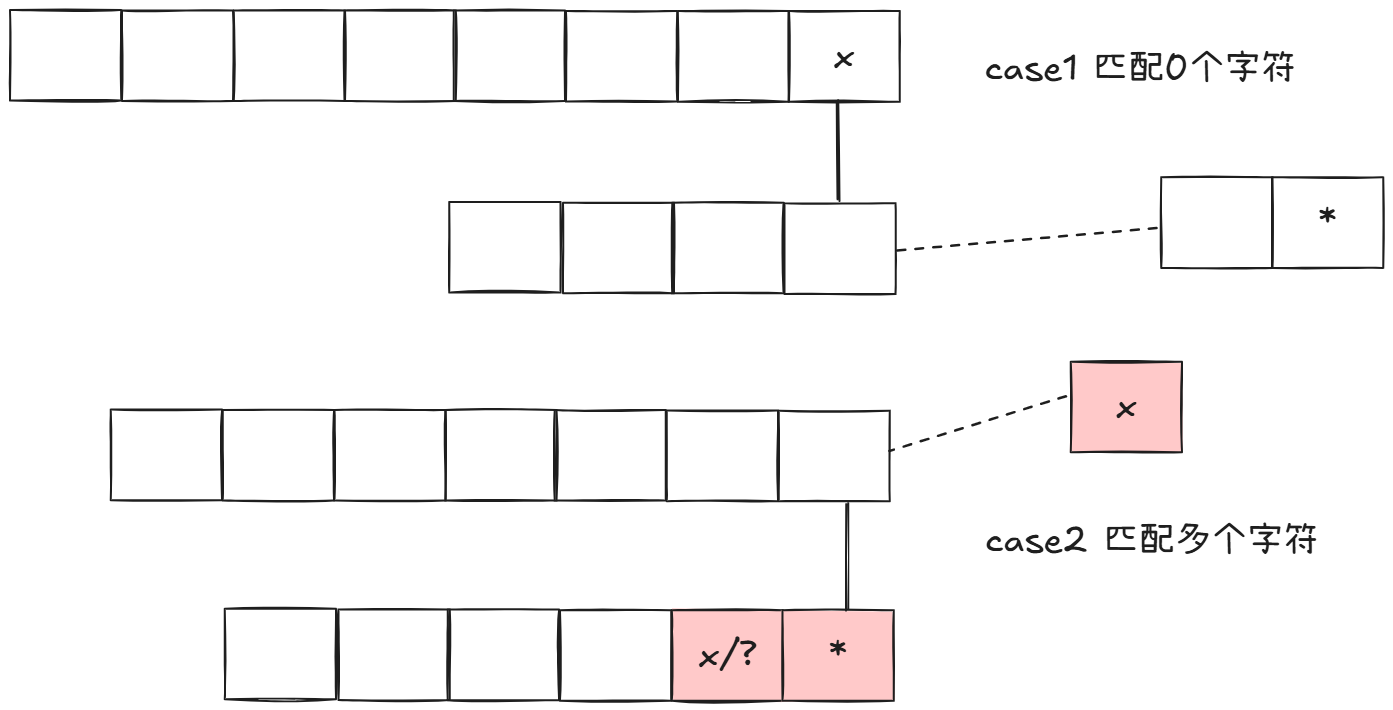
注意匹配多个字符的情况下,模式串的倒数第二个元素要和原串最后一个元素匹配,否则就是false.

最终状态表示:

dp[i][j]:s以i结尾的前缀和p以j为结尾的前缀能否匹配.

注意这里初始化和上一题类似,但是我们的'*'是要间隔才能匹配空串.

具体实现:

class Solution {
public:
    bool isMatch(string s, string p) {
        int m=s.size(),n=p.size();
        vector<vector<bool>>dp(m+1,vector<bool>(n+1));
        dp[0][0]=true;
        for(int j=2;j<=n;j+=2){
            if(p[j-1]!='*')break;
            dp[0][j]=true;
        }
        for(int i=1;i<=m;++i){
            for(int j=1;j<=n;++j){
                if(s[i-1]==p[j-1]||p[j-1]=='.')dp[i][j]=dp[i-1][j-1];
                else if(p[j-1]=='*'){
                    dp[i][j]=dp[i][j-2];//丢弃
                    if(!dp[i][j-2]&&(s[i-1]==p[j-2]||p[j-2]=='.'))
                        dp[i][j]=dp[i-1][j];
                }
            }
        }
        return dp[m][n];
    }
};

时间复杂度和空间复杂度都是O(mn)

同样的我们可以进行空间优化:

class Solution {
public:
    bool isMatch(string s, string p) {
        int m=s.size(),n=p.size();
        bool cur,prev;
        vector<bool>dp(n+1);
        prev=true;
        for(int j=2;j<=n;j+=2){
            if(p[j-1]!='*')break;
            dp[j]=true;
        }
        for(int i=1;i<=m;++i){
            if(i>1)prev=false;//s不空，p空，false
            for(int j=1;j<=n;++j){
                cur=dp[j];
                if(s[i-1]==p[j-1]||p[j-1]=='.')dp[j]=prev;
                else if(p[j-1]=='*'){
                    dp[j]=dp[j-2];//丢弃
                    if(!dp[j]&&(s[i-1]==p[j-2]||p[j-2]=='.'))//匹配多个
                        dp[j]=cur;
                }else{
                    dp[j]=false;
                }
                prev=cur;
            }
        }
        return dp[n];
    }
};

时间复杂度O(mn),空间复杂度O(n).

交错字符串

题目描述

交错字符串

给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。

两个字符串 s 和 t 交错 的定义与过程如下，其中每个字符串都会被分割成若干 非空 子字符串：

s = s1 + s2 + ... + sn

t = t1 + t2 + ... + tm

|n - m| <= 1

交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...

注意：a + b 意味着字符串 a 和 b 连接。

示例 1：

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"

输出：true

示例 2：

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"

输出：false

示例 3：

输入：s1 = "", s2 = "", s3 = ""

输出：true

提示：

• 0 <= s1.length, s2.length <= 100

• 0 <= s3.length <= 200

• s1、s2、和 s3 都由小写英文字母组成

• 进阶：您能否仅使用 O(s2.length) 额外的内存空间来解决它?

算法原理和实现

实际上只要s1和s2的子序列能拼接成s3,那么都是交错拼接.

我们考虑状态表示为:

dp[i][j]为s1以i为结尾的前缀和s2以j为结尾的前缀能否交错拼接成s3以i+j+1为结尾的前缀.

那么分为四种情况:

1. s1[i]==s2[j]==s3[i+j+1]
   那么拼接的交错序列既有可能以s1[i]结尾,也有可能以s2[j]结尾
2. s1[i]==s3[i+j+1]
   那么一定以s1[i]结尾
3. s2[j]==s3[i+j+1]
   那么一定以s2[j]结尾
4. 其他情况,一定不能拼接.

此外我们需要注意初始化,如果我们给dp表多申请一行一列.那么第一行就是s1前缀为空的时候,s2的前缀必须和s3的前缀完全相等才是true,只要出现一个不相等的字符后续都是false.

第一列也是同理.

具体实现:

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        int len1=s1.size(),len2=s2.size(),len3=s3.size();
        if(len1+len2!=len3)return false;
        vector<vector<bool>>dp(len1+1,vector<bool>(len2+1));
        dp[0][0]=true;
        for(int i=1;i<=len2;++i){
            if(s2[i-1]!=s3[i-1])break;
            dp[0][i]=true;
        }
        for(int i=1;i<=len1;++i){
            if(s1[i-1]!=s3[i-1])break;
            dp[i][0]=true;
        }
        for(int i=1;i<=len1;++i){
            for(int j=1;j<=len2;++j){
                if(s1[i-1]==s2[j-1]&&s1[i-1]==s3[i+j-1]){
                    dp[i][j]=dp[i][j-1]||dp[i-1][j];
                }else if(s1[i-1]==s3[i+j-1]){
                    dp[i][j]=dp[i-1][j];
                }else if(s2[j-1]==s3[i+j-1]){
                    dp[i][j]=dp[i][j-1];
                }
            }
        }
        return dp[len1][len2];
    }
};

时间复杂度和空间复杂度都是O(mn).

同样的我们只借助上一行的状态,因此可以进行空间优化:

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        int m=s1.size(),n=s2.size();
        if(m+n!=s3.size())return false;
        if(m<n){
            swap(m,n);
            swap(s1,s2);
        }
        if(!n)return s1==s3;
        vector<bool>dp(n+1);
        dp[0]=true;
        //s1为空时
        for(int i=1;i<=n;++i){
            if(s2[i-1]!=s3[i-1])break;
            dp[i]=true;
        }
        for(int i=1;i<=m;++i){
            //比较s2为空时
            if(s1[i-1]!=s3[i-1])dp[0]=false;
            for(int j=1;j<=n;++j){
                if(s1[i-1]==s2[j-1]&&s1[i-1]==s3[i+j-1]){
                    dp[j]=dp[j-1]||dp[j];//说明有可能取到dp[0]
                }else if(s1[i-1]==s3[i+j-1]){
                    continue;
                }else if(s2[j-1]==s3[i+j-1]){
                    dp[j]=dp[j-1];
                }else{
                    dp[j]=false;
                }
            }
        }
        return dp[n];
    }
};

时间复杂度O(mn),空间复杂度O(min(m,n)).

两个字符串的最小ASCII删除和

题目描述

两个字符串的最小ASCII删除和

给定两个字符串s1 和 s2，返回 使两个字符串相等所需删除字符的 ASCII 值的最小和 。

示例 1:

输入: s1 = "sea", s2 = "eat"

输出: 231

解释: 在 "sea" 中删除 "s" 并将 "s" 的值(115)加入总和。

在 "eat" 中删除 "t" 并将 116 加入总和。

结束时，两个字符串相等，115 + 116 = 231 就是符合条件的最小和。

示例 2:

输入: s1 = "delete", s2 = "leet"

输出: 403

解释: 在 "delete" 中删除 "dee" 字符串变成 "let"，

将 100[d]+101[e]+101[e] 加入总和。在 "leet" 中删除 "e" 将 101[e] 加入总和。

结束时，两个字符串都等于 "let"，结果即为 100+101+101+101 = 403 。

如果改为将两个字符串转换为 "lee" 或 "eet"，我们会得到 433 或 417 的结果，比答案更大。

提示:

• 1 <= s1.length, s2.length <= 1000
• s1 和 s2 由小写英文字母组成

算法原理和实现

根据经验,我们定义dp[i][j]为使得s1以i为结尾的前缀和s2以j为结尾的前缀要删除的最小ascll码值.

那么当s1[i]==s2[j]时,势必不用删除最后一个元素,dp[i][j]=dp[i-1][j-1].

当s1[i]!=s2[j]时,势必要删掉s1[i]或者s2[j]中的一个,我们选取删掉一个情况的最小值:dp[i][j]=min(dp[i-1][j]+s1[i],dp[i][j-1]+s2[j])

此外要注意初始化.如果我们给dp表多开一行一列,那么第一行就是完全删除s2[j]的前缀,第一列就是完全删除s1[i]的前缀.

具体实现:

class Solution {
public:
    int minimumDeleteSum(string s1, string s2) {
        int m=s1.size(),n=s2.size();
        vector<vector<int>>dp(m+1,vector<int>(n+1));
        for(int i=1;i<=n;++i)dp[0][i]=dp[0][i-1]+s2[i-1];
        for(int i=1;i<=m;++i)dp[i][0]=dp[i-1][0]+s1[i-1];
        for(int i=1;i<=m;++i){
            for(int j=1;j<=n;++j){
                if(s1[i-1]==s2[j-1])dp[i][j]=dp[i-1][j-1];
                else dp[i][j]=min(dp[i-1][j]+s1[i-1],dp[i][j-1]+s2[j-1]);
            }
        }
        return dp[m][n];
    }
};

时间复杂度和空间复杂度都是O(mn).

显然我们每一次更新都只需要借助上一行的状态,我们可以进行状态压缩:

class Solution {
public:
    int minimumDeleteSum(string s1, string s2) {
        int m=s1.size(),n=s2.size(),cur,prev;
        if(m<n){
            swap(m,n);
            swap(s1,s2);
        }
        vector<int>dp(n+1);
        for(int i=1;i<=n;++i)dp[i]=dp[i-1]+s2[i-1];
        for(int i=1;i<=m;++i){
            prev=dp[0];
            dp[0]+=s1[i-1];
            for(int j=1;j<=n;++j){
                cur=dp[j];
                if(s1[i-1]==s2[j-1])dp[j]=prev;
                else dp[j]=min(cur+s1[i-1],dp[j-1]+s2[j-1]);
                prev=cur;
            }
        }
        return dp[n];
    }
};

时间复杂度O(mn),空间复杂度O(min(m,n))

最长重复子数组

题目描述

最长重复子数组

给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

示例 1：

输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]

输出：3

解释：长度最长的公共子数组是 [3,2,1] 。

示例 2：

输入：nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]

输出：5

提示：

• 1 <= nums1.length, nums2.length <= 1000
• 0 <= nums1[i], nums2[i] <= 100

算法原理和实现

根据经验,我们定义状态表示为:

dp[i][j]为nums1中以i为结尾的所有子数组和nums2中以j为结尾的左右子数组的最大公共子数组.

显然当nums1[i]!=nums2[j]时,dp[i][j]=0.

否则就能拼接上dp[i-1][j-1]

具体实现:

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        int m=nums1.size(),n=nums2.size(),ret=0;
        vector<vector<int>>dp(m+1,vector<int>(n+1));
        for(int i=1;i<=m;++i){
            for(int j=1;j<=n;++j){
                if(nums1[i-1]!=nums2[j-1])dp[i][j]=0;
                else dp[i][j]=dp[i-1][j-1]+1;
                ret=max(ret,dp[i][j]);
            }
        }
        return ret;
    }
};

时间复杂度和空间复杂度都是O(mn)

进一步空间优化:

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        int m=nums1.size(),n=nums2.size(),ret=0,prev,cur;
        if(m<n){
            swap(m,n);
            swap(nums1,nums2);
        }
        vector<int>dp(n+1);
        for(int i=0;i<m;++i){
            prev=0;
            for(int j=0;j<n;++j){
                cur=dp[j];
                if(nums1[i]!=nums2[j])dp[j]=0;
                else dp[j]=prev+1;
                ret=max(ret,dp[j]);
                prev=cur;
            }
        }
        return ret;
    }
};

时间复杂度O(mn),空间复杂度O(min(m,n)).