不错的 Div3。
比赛链接:CodeForces
A - Sieve of Erato67henes
给定
n个正整数 a 1 , a 2 , ... , a n a_1, a_2, \dots, a_n a1,a2,...,an,判断是否可以从这些数中选择任意数量(至少一个)的元素,使它们的乘积恰好为 67 67 67。共有
t组测试数据 ( 1 ≤ t ≤ 10 4 1 \le t \le 10^4 1≤t≤104),每组数据包含n个数 ( 1 ≤ n ≤ 5 1 \le n \le 5 1≤n≤5),每个数 a i a_i ai 满足 ( 1 ≤ a i ≤ 67 1 \le a_i \le 67 1≤ai≤67)。
不难发现 67 67 67 是个质数,所以这等价于询问 a i a_i ai 中有没有 67 67 67。
cpp
#include <bits/stdc++.h>
using namespace std;
void work() {
int n; cin >> n; int ans = 0;
for (int i = 1; i <= n; ++i) {
int u; cin >> u; if (u == 67) ans = 1;
}
cout << (ans ? "YES" : "NO") << '\n';
}
int main() {
int T; cin >> T;
while (T--) work();
return 0;
}B - Heapify 1
给定一个长度为 N N N 的排列 a a a。可以重复执行操作:选择索引 i i i ( 1 ≤ i ≤ N / 2 1 \le i \le N/2 1≤i≤N/2),交换 a i a_i ai 和 a 2 i a_{2i} a2i。判断序列 a a a 是否能通过这些操作排序成升序。
数据范围: 1 ≤ t ≤ 10 4 1 \le t \le 10^4 1≤t≤104, 1 ≤ n ≤ 2 ⋅ 10 5 1 \le n \le 2 \cdot 10^5 1≤n≤2⋅105,所有测试用例的 n n n 之和不超过 2 ⋅ 10 5 2 \cdot 10^5 2⋅105。
考虑依次将值为 i i i 的位置(设为 p o s pos pos),然后移动到 i i i。
不难发现只能是一直 p o s ← p o s 2 pos \leftarrow \frac{pos}{2} pos←2pos,直到 p o s = i pos = i pos=i。若中途 p o s pos pos 为奇数或者最终 p o s pos pos 做不到等于 i i i,那么显然输出 NO。
由于每次 p o s pos pos 都会除以 2 2 2,所以最终的时间复杂度为 O ( ∑ N log N ) O(\sum N \log N) O(∑NlogN)。
cpp
#include <bits/stdc++.h>
using namespace std;
const int N = 200000;
int n, a[N + 10], pos[N + 10];
void Swap(int u, int v) {
swap(a[u], a[v]); swap(pos[a[u]], pos[a[v]]);
}
void work() {
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> a[i]; pos[a[i]] = i;
}
for (int i = 1; i <= n; ++i) {
while (pos[i] > i) {
if (pos[i] & 1) {
cout << "NO" << '\n'; return;
}
Swap(pos[i] >> 1, pos[i]);
}
if (pos[i] < i) {
cout << "NO" << '\n'; return;
}
}
cout << "YES" << '\n';
}
int main() {
int T; cin >> T;
while (T--) work();
return 0;
}C - Dice Roll Sequence
给定含1-6整数的序列
a,可修改一个元素。目标:将序列变为"骰子掷出序列",即相邻元素需代表骰子相邻面。骰子面x与7-x对面(不相邻)。求最少操作数。数据范围:
1 <= t <= 10^4,1 <= n <= 3*10^5,sum(n)<=3*10^5,1 <= a[i] <= 6。
考虑 dp,设 d p ( i , j ) dp(i, j) dp(i,j) 表示将 a 1 ∼ a i a_1 \sim a_i a1∼ai 进行一定赋值操作,使得 a i = j a_i = j ai=j 且 a 1 ∼ a i a_1 \sim a_i a1∼ai 为合法骰子数列的最小赋值操作数。
不难得出以下状态转移方程:
d p ( i , j ) = min j + k ≠ 7 , j ≠ k { d p ( i − 1 , k ) } + [ a i ≠ j ] dp(i, j) = \min_{j + k \neq 7, j \neq k} \{ dp(i - 1, k) \} + [a_i \neq j] dp(i,j)=j+k=7,j=kmin{dp(i−1,k)}+[ai=j]
时间复杂度 O ( ∑ 36 n ) O(\sum 36 n) O(∑36n)。
cpp
#include <bits/stdc++.h>
using namespace std;
const int N = 300000;
int n;
int a[N + 10], dp[N + 10][7];
void work() {
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
for (int i = 1; i <= n; ++i) {
memset(dp[i], 0x3f, sizeof(dp[i]));
for (int x = 1; x <= 6; ++x) {
for (int y = 1; y <= 6; ++y) {
if (x + y == 7 || x == y) continue;
dp[i][x] = min(dp[i][x], dp[i - 1][y] + (a[i] == x ? 0 : 1));
}
}
}
int ans = 0x3f3f3f3f;
for (int i = 1; i <= 6; ++i) ans = min(ans, dp[n][i]);
cout << ans << '\n';
}
int main() {
int T; cin >> T;
while (T--) work();
return 0;
}D - Absolute Cinema
给出一个含 n n n 个整数的隐藏序列 a 1 , ... , a n a_1, \dots, a_n a1,...,an,其中 ∣ a i ∣ ≤ 1000 |a_i| \le 1000 ∣ai∣≤1000。定义函数 f ( x ) = ∑ i = 1 n a i ⋅ ∣ i − x ∣ f(x) = \sum_{i=1}^{n} a_i \cdot |i - x| f(x)=∑i=1nai⋅∣i−x∣。现在给出 n n n 个函数值 f ( 1 ) , f ( 2 ) , ... , f ( n ) f(1), f(2), \dots, f(n) f(1),f(2),...,f(n),要求确定原始序列 a 1 , a 2 , ... , a n a_1, a_2, \dots, a_n a1,a2,...,an。保证 a i a_i ai 能唯一确定。
数据范围: t ≤ 10 4 t \le 10^4 t≤104, 2 ≤ n ≤ 300000 2 \le n \le 300000 2≤n≤300000 (所有测试用例的 n n n 之和不超过 300000 300000 300000), − 10 14 ≤ f ( i ) ≤ 10 14 -10^{14} \le f(i) \le 10^{14} −1014≤f(i)≤1014。
推式子题,这种看起来就是要差分。
不难发现 f ( x + 1 ) − f ( x ) = 2 ∑ i = 1 x a i − ∑ i = 1 n a i f(x + 1) - f(x) = 2 \sum_{i = 1}^x a_i - \sum_{i = 1}^n a_i f(x+1)−f(x)=2∑i=1xai−∑i=1nai,那么 f ( x + 2 ) + f ( x ) = ( f ( x + 2 ) − f ( x + 1 ) ) − ( f ( x + 1 ) − f ( x ) ) = 2 a x + 1 f(x + 2) + f(x) = (f(x + 2) - f(x + 1)) - (f(x + 1) - f(x)) = 2 a_{x + 1} f(x+2)+f(x)=(f(x+2)−f(x+1))−(f(x+1)−f(x))=2ax+1。
即 ∀ x ∈ [ 2 , n − 1 ] \forall x \in [2, n - 1] ∀x∈[2,n−1], a x = f ( x + 1 ) + f ( x − 1 ) 2 a_x = \frac{f(x + 1) + f(x - 1)}{2} ax=2f(x+1)+f(x−1)。
得到了 a x , x ∈ [ 2 , n − 1 ] a_x, x \in [2, n - 1] ax,x∈[2,n−1] 后,我们很容易得到 a 1 a_1 a1 和 a n a_n an:
a 1 = f ( n ) − ∑ i = 2 n − 1 a i ( n − i ) n − 1 , a n = f ( 1 ) − ∑ i = 2 n − 1 a i ( i − 1 ) n − 1 a_1 = \frac{f(n) - \sum_{i = 2}^{n - 1} a_i (n - i)}{n - 1}, a_n = \frac{f(1) - \sum_{i = 2}^{n - 1} a_i (i - 1)}{n - 1} a1=n−1f(n)−∑i=2n−1ai(n−i),an=n−1f(1)−∑i=2n−1ai(i−1)
时间复杂度 O ( ∑ n ) O(\sum n) O(∑n)。
cpp
#include <bits/stdc++.h>
using namespace std;
const int N = 300000;
int n;
long long f[N + 10], d[N + 10], a[N + 10];
void work() {
cin >> n;
for (int i = 1; i <= n; ++i) cin >> f[i];
for (int i = 1; i < n; ++i) d[i] = f[i + 1] - f[i];
for (int i = 2; i < n; ++i) a[i] = (d[i] - d[i - 1]) / 2;
a[1] = f[n], a[n] = f[1];
for (int i = 2; i < n; ++i) {
a[1] -= a[i] * abs(n - i), a[n] -= a[i] * abs(1 - i);
}
a[1] /= n - 1, a[n] /= n - 1;
for (int i = 1; i <= n; ++i) cout << a[i] << ' ';
cout << '\n';
}
int main() {
int T; cin >> T;
while (T--) work();
return 0;
}E - Idiot First Search
Bob在一个
n+1节点的二叉树中从k到0。他的移动规则是:叶子节点向上,非叶子节点无标记写'L'左移,有'L'写'R'右移,有'R'擦除向上。求k=1...n出发到0所需时间模10^9+7。数据范围:t <= 10^4, 1 <= n <= 300001(n为奇数),sum n <= 300001。
考虑 dp,设 d p ( i ) dp(i) dp(i) 表示以 i i i 为起点,走遍子树后回到 i i i 需要多少步,不难得出状态转移方程:
- 若 i i i 为叶子: d p ( i ) = 0 dp(i) = 0 dp(i)=0。
- 若 i i i 非叶子: d p ( i ) = d p ( l s i ) + d p ( r s i ) + 4 dp(i) = dp(ls_i) + dp(rs_i) + 4 dp(i)=dp(lsi)+dp(rsi)+4。
那么节点 i i i 的答案就是 d p i + d p f a i + d p f a f a i + ⋯ + d p 1 + 1 dp_i + dp_{fa_i} + dp_{fa_{fa_i}} + \dots + dp_1 + 1 dpi+dpfai+dpfafai+⋯+dp1+1,这个可以 dfs 一遍求解。
时间复杂度 O ( ∑ n ) O(\sum n) O(∑n)。
cpp
#include <bits/stdc++.h>
using namespace std;
const int N = 300001;
const long long mod = 1000000007LL;
int n;
int ls[N + 10], rs[N + 10];
long long dp[N + 10], ans[N + 10];
void dfs1(int u) {
dp[u] = 0;
if (!ls[u]) return;
dfs1(ls[u]); dfs1(rs[u]);
dp[u] = (dp[ls[u]] + dp[rs[u]] + 4) % mod;
}
void dfs2(int u) {
ans[u] = (ans[u] + dp[u]) % mod;
if (!ls[u]) return;
ans[ls[u]] = ans[rs[u]] = (ans[u] + 1) % mod;
dfs2(ls[u]); dfs2(rs[u]);
}
void work() {
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> ls[i] >> rs[i]; ans[i] = 0;
}
dfs1(1); dfs2(1);
for (int i = 1; i <= n; ++i) cout << (ans[i] + 1) % mod << ' ';
cout << '\n';
}
int main() {
int T; cin >> T;
while (T--) work();
return 0;
}F - Parabola Independence
题目给定 n n n 个二次函数 f i ( x ) = a i x 2 + b i x + c i f_i(x)=a_ix^2+b_ix+c_i fi(x)=aix2+bix+ci。
若两函数 f , g f, g f,g 无交点,则称其"独立"。若一个函数集合中任意两函数皆独立,则称其"有序"。对于每个 f i f_i fi,求包含 f i f_i fi 的最大有序子集规模。
数据范围: t ∈ [ 1 , 10 4 ] , n ∈ [ 1 , 3000 ] , a i , b i , c i ∈ [ − 10 6 , 10 6 ] t \in [1, 10^4], n \in [1, 3000], a_i, b_i, c_i \in [-10^6, 10^6] t∈[1,104],n∈[1,3000],ai,bi,ci∈[−106,106] ( a i ≠ 0 a_i \ne 0 ai=0)。函数互不相同, ∑ n 2 ≤ 3000 2 \sum n^2 \le 3000^2 ∑n2≤30002。
我们回忆一下二次函数的判别式: Δ = b 2 − 4 a c \Delta = b^2 - 4 a c Δ=b2−4ac。
那么两个二次函数 f u ( x ) f_u(x) fu(x) 和 f v ( x ) f_v(x) fv(x) 不相交等价于 ( b u − b v ) 2 < 4 ( a u − a v ) ( c u − c v ) , a u ≠ a v (b_u - b_v)^2 < 4 (a_u - a_v) (c_u - c_v), a_u \neq a_v (bu−bv)2<4(au−av)(cu−cv),au=av,或者 a u = a v , b u = b v , c u ≠ c v a_u = a_v, b_u = b_v, c_u \neq c_v au=av,bu=bv,cu=cv。
由于 ( b u − b v ) 2 (b_u - b_v)^2 (bu−bv)2 非负,我们可以发现这其实是一个偏序关系(如果我们强制 a u = a v , b u = b v , c u < c v a_u = a_v, b_u = b_v, c_u < c_v au=av,bu=bv,cu<cv)!
那么考虑按 a , b , c a, b, c a,b,c 关键字排序后 dp,令 p r e i pre_i prei 表示最多包含 1 ∼ i 1 \sim i 1∼i 个二次函数(包括 i i i), s u f i suf_i sufi 表示最多包含 i ∼ n i \sim n i∼n 个二次函数(包括 i i i)。
状态转移方程很显然(就是那上面的判断式子判断一下就可以了),答案就是 p r e i + s u f i = 1 pre_i + suf_i = 1 prei+sufi=1,时间复杂度 O ( ∑ n 2 ) O(\sum n^2) O(∑n2)
cpp
#include <bits/stdc++.h>
using namespace std;
const int N = 3000;
struct bruh {
long long a, b, c; int id;
}f[N + 10];
int n, pre[N + 10], suf[N + 10], ans[N + 10];
bool check(bruh u, bruh v) {
if (u.a < v.a) {
return (u.b - v.b) * (u.b - v.b) < 4LL * (u.a - v.a) * (u.c - v.c);
}
return u.a == v.a && u.b == v.b && u.c < v.c;
}
bool cmp(bruh u, bruh v) {
if (u.a != v.a) return u.a < v.a;
if (u.b != v.b) return u.b < v.b;
return u.c < v.c;
}
void work() {
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> f[i].a >> f[i].b >> f[i].c; f[i].id = i;
}
sort(f + 1, f + n + 1, cmp);
for (int i = 1; i <= n; ++i) {
pre[i] = 1;
for (int j = 1; j < i; ++j) {
if (check(f[j], f[i])) pre[i] = max(pre[i], pre[j] + 1);
}
}
for (int i = n; i >= 1; --i) {
suf[i] = 1;
for (int j = n; j > i; --j) {
if (check(f[i], f[j])) suf[i] = max(suf[i], suf[j] + 1);
}
}
for (int i = 1; i <= n; ++i) {
ans[f[i].id] = pre[i] + suf[i] - 1;
}
for (int i = 1; i <= n; ++i) cout << ans[i] << ' ';
cout << '\n';
}
int main() {
int T; cin >> T;
while (T--) work();
return 0;
}G - Idiot First Search and Queries
在一个 N + 1 N+1 N+1 顶点的二叉树(根0, N N N 奇数),Bob按"愚蠢搜索"移动:叶子回父;节点空则写"I"去左子;"I"则写"R"去右子;"R"则擦除去父。每步1秒。对 q q q 个查询,给定 v j , k j v_j, k_j vj,kj,求 k j k_j kj 步后Bob位置。
数据范围: t ≤ 10 4 , N ≤ 300001 t \le 10^4, N \le 300001 t≤104,N≤300001(奇数), q ≤ 400000 q \le 400000 q≤400000; 且 s u m ( N ) ≤ 300001 , s u m ( q ) ≤ 400000 sum(N) \le 300001, sum(q) \le 400000 sum(N)≤300001,sum(q)≤400000; 0 ≤ k j < min ( 10 9 + 7 , T v j ) 0 \le k_j < \min(10^9+7, T_{v_j}) 0≤kj<min(109+7,Tvj)。
为了方便,我们将重新定义 E 题中的数组。
设 s z ( i ) sz(i) sz(i) 为子树大小, d p ( i ) dp(i) dp(i) 为 E 题中的答案减 1 1 1。
我们可以发现:Bob 的移动路径实际上是一直跳父亲 u → f a u → ⋯ → c u r u \to fa_u \to \dots \to cur u→fau→⋯→cur,直到没有足够的步数使得 c u r → f a c u r cur \to fa_{cur} cur→facur,这个可以用倍增找到对应的 c u r cur cur。
然后我们考虑跳到 c u r cur cur 后的移动,不难发现其实是在按照欧拉序列上的顺序走,那么预处理一下欧拉序列即可。
时间复杂度 O ( ( n + q ) log n ) O((n + q) \log n) O((n+q)logn)。
cpp
#include <bits/stdc++.h>
using namespace std;
const int N = 300001, B = 19;
int n, q;
int ls[N + 10], rs[N + 10];
int fa[B + 1][N + 10];
int sz[N + 10]; long long dp[N + 10];
int et[2 * N + 10], pos[N + 10], cnt;
void dfs1(int u) {
for (int i = 1; i <= B; ++i) fa[i][u] = fa[i - 1][fa[i - 1][u]];
sz[u] = 1, dp[u] = 0;
if (!ls[u]) return;
fa[0][ls[u]] = u, fa[0][rs[u]] = u;
dfs1(ls[u]); dfs1(rs[u]);
sz[u] += sz[ls[u]] + sz[rs[u]];
}
void dfs2(int u) {
dp[u] = dp[fa[0][u]] + 2LL * sz[u] - 1LL;
if (!ls[u]) return;
dfs2(ls[u]); dfs2(rs[u]);
}
void dfs3(int u) {
et[++cnt] = u; if (!pos[u]) pos[u] = cnt;
if (!ls[u]) return;
dfs3(ls[u]); et[++cnt] = u;
dfs3(rs[u]); et[++cnt] = u;
}
void work() {
cin >> n >> q; cnt = 0;
for (int i = 1; i <= n; ++i) {
cin >> ls[i] >> rs[i]; fa[0][i] = pos[i] = 0;
}
dfs1(1); dfs2(1); dfs3(1);
while (q--) {
int u, k; cin >> u >> k;
int cur = u;
for (int i = B; i >= 0; --i) {
if (fa[i][cur] && dp[u] - dp[fa[i][cur]] <= k) cur = fa[i][cur];
}
cout << et[pos[cur] + k - (dp[u] - dp[cur])] << ' ';
}
cout << '\n';
}
int main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int T; cin >> T;
while (T--) work();
return 0;
}H - Codeforces Heuristic Contest 001
给定一个 3 n × 3 n 3n \times 3n 3n×3n 的整数点网格,其中点的坐标 ( x , y ) (x, y) (x,y) 满足 1 ≤ x , y ≤ 3 n 1 \le x, y \le 3n 1≤x,y≤3n。任务是找到一个最大规模的三角形集合,需满足以下条件:
- 每个三角形的顶点必须恰好是网格上的三个不同的点。
- 每个三角形的面积必须恰好为 1 2 \frac{1}{2} 21,注意它们不一定是直角三角形。
- 集合中任意两个不同的三角形,不能有任何公共的交点,包括它们的顶点。
如果存在多个满足条件的最大规模集合,输出其中任意一个即可。1 ≤ t ≤ 30 1 \le t \le 30 1≤t≤30, 1 ≤ n ≤ 166 1 \le n \le 166 1≤n≤166, 所有测试用例中 n 2 n^2 n2 的总和不超过 166 2 166^2 1662。
诈骗题。首先不难得出答案上界为 3 n 2 3 n^2 3n2。
若 n n n 为偶数,不难想到将网格分为若干个 2 × 3 2 \times 3 2×3 或者若干个 3 × 2 3 \times 2 3×2 的小格子,每个小格子用 2 2 2 个三角形覆盖,即可做到 3 n 2 3 n^2 3n2。
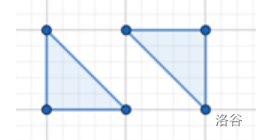
( 2 × 3 2 \times 3 2×3 的小格子)
若 n n n 为奇数(特判 n = 1 n = 1 n=1),咋一看好像没什么思路。我们可以先爆搜出 n = 3 n = 3 n=3 时候的答案,然后剩下的网格也可以分为若干个 2 × 3 2 \times 3 2×3 和 3 × 2 3 \times 2 3×2 的小格子,也可以做到 3 n 2 3 n^2 3n2。
最终时间复杂度 O ( ∑ n 2 ) O(\sum n^2) O(∑n2)。
cpp
#include <bits/stdc++.h>
using namespace std;
const int n3[27][6] = {
{1, 1, 1, 2, 2, 1}, {1, 3, 1, 4, 2, 2}, {1, 5, 1, 6, 2, 3},
{1, 7, 1, 8, 2, 4}, {1, 9, 2, 5, 2, 6}, {2, 7, 2, 8, 3, 1},
{2, 9, 3, 2, 3, 3}, {3, 4, 3, 5, 4, 1}, {3, 6, 3, 7, 4, 2},
{3, 8, 3, 9, 4, 3}, {4, 4, 4, 5, 5, 1}, {4, 6, 4, 7, 5, 2},
{4, 8, 4, 9, 5, 3}, {5, 4, 5, 5, 6, 1}, {5, 6, 5, 7, 6, 2},
{5, 8, 5, 9, 6, 3}, {6, 4, 6, 5, 7, 1}, {6, 6, 6, 7, 7, 2},
{6, 8, 6, 9, 7, 3}, {7, 4, 7, 5, 8, 1}, {7, 6, 7, 7, 8, 2},
{7, 8, 7, 9, 8, 3}, {8, 4, 8, 5, 9, 1}, {8, 6, 9, 2, 9, 3},
{8, 7, 9, 4, 9, 5}, {8, 8, 9, 6, 9, 7}, {8, 9, 9, 8, 9, 9}
};
int n;
void work() {
cin >> n;
if (n % 2 == 0) {
cout << 3 * n * n << '\n';
for (int i = 1; i < 3 * n; i += 3) {
for (int j = 1; j < 3 * n; j += 2) {
cout << i << ' ' << j << ' ' << i << ' ' << j + 1 << ' ' << i + 1 << ' ' << j << '\n';
cout << i + 1 << ' ' << j + 1 << ' ' << i + 2 << ' ' << j + 1 << ' ' << i + 2 << ' ' << j << '\n';
}
}
}
else {
if (n == 1) {
cout << 2 << '\n';
cout << "1 1 1 2 2 1" << '\n';
cout << "2 3 3 2 3 3" << '\n';
return;
}
cout << 3 * n * n << '\n';
for (int i = 0; i < 27; ++i) {
cout << n3[i][0] << ' ' << n3[i][1] << ' ' << n3[i][2] << ' ' << n3[i][3] << ' ' << n3[i][4] << ' ' << n3[i][5] << '\n';
}
for (int i = 10; i < 3 * n; i += 2) {
for (int j = 1; j < 3 * n; j += 3) {
cout << i << ' ' << j << ' ' << i + 1 << ' ' << j << ' ' << i << ' ' << j + 1 << '\n';
cout << i + 1 << ' ' << j + 1 << ' ' << i + 1 << ' ' << j + 2 << ' ' << i << ' ' << j + 2 << '\n';
}
}
for (int i = 1; i < 10; i += 3) {
for (int j = 10; j < 3 * n; j += 2) {
cout << i << ' ' << j << ' ' << i << ' ' << j + 1 << ' ' << i + 1 << ' ' << j << '\n';
cout << i + 1 << ' ' << j + 1 << ' ' << i + 2 << ' ' << j + 1 << ' ' << i + 2 << ' ' << j << '\n';
}
}
}
}
int main() {
int T; cin >> T;
while (T--) work();
return 0;
}