【题目描述】
有一棵二叉苹果树,如果数字有分叉,一定是分两叉,即没有只有一个儿子的节点。这棵树共 N 个节点,标号 1 至 N,树根编号一定为 1。
我们用一根树枝两端连接的节点编号描述一根树枝的位置。一棵有四根树枝的苹果树,因为树枝太多了,需要剪枝。但是一些树枝上长有苹果,给定需要保留的树枝数量,求最多能留住多少苹果。
【输入】
第一行两个数 N 和 Q ,N 表示树的节点数,Q 表示要保留的树枝数量。
接下来 N−1 行描述树枝信息,每行三个整数,前两个是它连接的节点的编号,第三个数是这根树枝上苹果数量。
【输出】
输出仅一行,表示最多能留住的苹果的数量。
【输入样例】
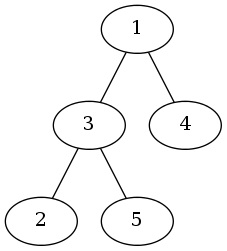
5 2
1 3 1
1 4 10
2 3 20
3 5 20【输出样例】
21【提示】
数据范围与提示:
对于 100% 的数据,1≤Q≤N≤100,N≠1,每根树枝上苹果不超过 30000 个。
在树形动态规划中,"树上背包"是一类非常经典的问题。它的特点是:我们需要在树形结构中选取若干节点或边,在满足"依赖关系"(选子节点必须选父节点)和"容量限制"(总数不超过Q)的前提下,使得总价值最大。
今天我们以经典题目 二叉苹果树 为例,深入剖析如何从零构建树形背包的状态转移方程,并掌握 O(NM) 的核心优化技巧。
1. 题目重述
题目描述:
有一棵N个节点的二叉树(根节点为 1),树枝上长有苹果。现在需要剪掉多余的树枝,只保留 Q根树枝。求在满足保留树枝数量不超过Q的前提下,能留住的最大苹果数量。
关键约束:
-
依赖性:如果想要保留子树中的树枝,必须先保留连接该子树的父节点树枝。
-
容量限制:树枝总数<=Q。
2. 算法核心:分组背包模型
这道题本质上是 "分组背包" 在树上的应用。
对于当前节点u,它的每一个子节点v及其子树,都可以看作是一个 "物品组"。
-
在这个"组"里,我们可以选择投入k个容量(树枝)。
-
不同的k对应不同的价值dp[v][k]。
-
我们需要在所有子节点(物品组)中分配总共j的容量,使得收益最大。
状态定义
- dp[u][j] :表示以u为根的子树中,保留j根树枝 所能获得的最大苹果数。
状态转移方程
对于节点u和它的一个子节点v(连接边的苹果数为w):
如果我们决定在v的子树里投入资源,那么:
-
必须先消耗1 根树枝用来连接
。
-
假设我们在v内部再分配k根树枝。
-
那么总消耗为k+1。
转移方程如下:
dp[u][j] =
其中:
-
j倒序遍历(类似 0/1 背包,防止重复利用同一个子树)。
-
k遍历子树可能的树枝分配数。
3. 代码细节
1. 双向存边与数组大小
题目输入不保证父子顺序,因此必须建立无向图 (双向addedge)。
-
易错点:N个点有N-1条边,双向存储需要2(N-1)的空间。
-
代码处理 :数组开到了
210(N<=100),完美避免了数组越界导致的RE或TLE。
2. 父节点判断 (防止死循环)
在DFS遍历邻接表时,由于是无向图,必须判断 if(v==fa)。
- 细节 :在
continue之前,必须执行p=nxt[p],否则指针卡死,导致死循环。代码中处理得非常严谨。
3. Size优化 (时间复杂度关键)
这是树形背包最核心的优化。如果不加优化,三层循环的复杂度接近O()。
加上sz数组记录子树大小后:
-
j的上限取
min(q,sz[x]-1)。 -
k的上限取
min(j,sz[v])-1。 -
这使得算法实际上只合并了每一对点一次,均摊复杂度降为
。
4. 完整代码展示
cpp
#include <iostream>
#include <cstring>//对应memset函数
#include <algorithm>//对应max函数
using namespace std;
int h[210];
int vtex[210];
int nxt[210];
int wt[210];
int idx;
int sz[110];//存储当前节点团队共有多少节点
//dp[i][j]代表当前是第i个节点的团队在可以保留j个数枝的情况下最大保留苹果数
int dp[110][110];
int n,q;
//存图
void addedge(int u,int v,int w){
vtex[idx]=v;
nxt[idx]=h[u];
wt[idx]=w;
h[u]=idx++;
}
void dfs(int x,int fa){//当前根节点 当前节点的父节点
sz[x]=1;//初始时,就只有自己 节点数为1
int p=h[x];
while(p!=-1){//遍历当前根节点的所有儿子
int v=vtex[p];
//如果当前根节点的子节点和父节点相同,就跳过
//因为我之前是存的双边,这一步目的是找到正确父子关系
if(v==fa) {
p=nxt[p];
continue;
}
dfs(v,x);//否则就递归到叶子结点开始计算
sz[x]+=sz[v];//子树的节点也要加入x团队
//分组背包,每个子树是一组物品,然后因为优化了一维(当前是哪颗子树)
//所以需要倒序遍历
//数枝数量背包容量最多取到min(q,sz[x]-1),最少有0根树枝
for(int j=min(q,sz[x]-1);j>=0;j--){
//分配给当前这个子树多少容量(数枝数量)
//k不能取到j,因为x连接子树根节点v就需要一颗树枝,所以子树最多得到j-1根树枝
//同时子树有sz[v]个节点,那最多能有sz[v]-1根树枝
for(int k=0;k<min(j,sz[v]);k++){
//这里要写dp[x][j-k-1]而不能写dp[x][j-k]
//因为连接子树也需要一根树枝
dp[x][j]=max(dp[x][j],dp[x][j-k-1]+dp[v][k]+wt[p]);
}
}
p=nxt[p];
}
}
int main(){
cin>>n>>q;
//初始化头指针数组为空
memset(h,-1,sizeof(h));
for(int i=1;i<n;i++){
int u,v,w;
cin>>u>>v>>w;
addedge(u,v,w);
addedge(v,u,w);//无向图存双边
}
dfs(1,0);//题目给出树根编号一定是1,根节点没有父节点
cout<<dp[1][q];
return 0;
}5. 总结
-
循环边界:
-
代码中
k<min(j, sz[v]) -
k<jk<=j-1(预留连接线)。 -
k<sz[v]k<=sz[v]-1(子树树枝上限)。 -
这保证了逻辑的严密性。
-
-
初始化:
-
sz[x]初始为 1(节点数)。 -
dp数组全局初始化为 0,符合题目逻辑(不保留树枝则价值为 0)。
-
-
复杂度:
- 利用
sz优化,我们将无效的状态转移全部剪枝,使得算法能在大数据范围下高效运行。
- 利用