一、基础知识
动态规划的问题经常要分类讨论,这是因为动态规划的问题本来就有「最优子结构」的特点,即大问题的最优解通常由小问题的最优解得到。
理解重点:就是当前的dp是否能通过之前的dp推出来

关键 1:理解题意
题目要我们找出和最大的连续子数组的值是多少,「连续」是关键字,连续很重要,不是子序列。
题目只要求返回结果,不要求得到最大的连续子数组是哪一个。这样的问题通常可以使用「动态规划」解决。
关键 2:如何定义子问题(如何定义状态)
设计状态思路:把不确定的因素确定下来,进而把子问题定义清楚,把子问题定义得简单。找到子问题之间的联系。动态规划的思想通过解决了一个一个简单的问题,进而把简单的问题的解组成了复杂的问题的解。
子问题 1:以−2 结尾的连续子数组的最大和是多少;
子问题 2:以1 结尾的连续子数组的最大和是多少;
子问题 3:以−3 结尾的连续子数组的最大和是多少;
子问题 4:以4 结尾的连续子数组的最大和是多少;
子问题 5:以−1 结尾的连续子数组的最大和是多少;
子问题 6:以2 结尾的连续子数组的最大和是多少;
子问题 7:以1 结尾的连续子数组的最大和是多少;
子问题 8:以−5 结尾的连续子数组的最大和是多少;
子问题 9:以4 结尾的连续子数组的最大和是多少。
如果编号为 i 的子问题的结果是负数或者 0 ,那么编号为 i + 1 的子问题就可以把编号为 i 的子问题的结果舍弃掉(这里 i 为整数,最小值为 1 ,最大值为 8)

关键3:返回值
返回值不一定是dp[length]

以n=3为例,根据头结点划分左右结点个数: 当1为结点时,左边结点0个,右边结点2个 = dp[0] * dp[2] 当2为结点时,左边结点1个,右边结点1个 = dp[1] * dp[1] 当3为结点时,左边结点2个,右边结点0个 = dp[2] * dp[0]
所以以dp[3]都可以通过dp[0]、dp[1]、dp[2]得到
递推公式:遍历头结点j(从1到n):dp[i] = dp[j-1] * dp[i-j]
二、动态规划问题分类
2.1 0-1背包问题
背包最大重量为4。 物品为: 重量 价值 物品0 1 15 物品1 3 20 物品2 4 30 问背包能背的物品最⼤价值是多少?
dp[i] [j] 表示从下标为[0-i]的物品⾥任意取,放进容量为j的背包,价值总和最⼤是多少。
不放物品i:由dp[i - 1][j]推出,即背包容量为j,⾥⾯不放物品i的最⼤价值,此时dp[i][j]就是dp[i - 1][j]。(其 实就是当物品i的重量⼤于背包j的重量时,物品i⽆法放进背包中,所以背包内的价值依然和前⾯相同。) 放物品i:由dp[i - 1][j-weight[i]]推出,dp为背包容dp[i - 1][j-weight[i]]量为j - weight[i]的时候不放物品i的最⼤价值,那么dp[i - 1][j-weight[i]]+ value[i] (物品i的价值),就是背包放物品i得到的最⼤价值 所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i−1][j-weight[i]]+ value[i]);
遍历顺序:从背包或者物品都可以
java
// weight数组的⼤⼩ 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}一维dp数组(滚动数组)
如果dp[i-1]那一层拷贝到dp[i]上,可以化简为
java
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);遍历顺序:只能是先便利物品,再遍历背包,而且遍历背包时,需要倒序遍历(为了保证物品i只被放⼊⼀次!)
java
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}0-1背包问题延申(两个维度的重量)

java
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int dp[][] = new int[m+1][n+1];
for (int i = 0; i < strs.length; i++) {
char[] chars = strs[i].toCharArray();
int one = 0;//记录每个物品的重量(one)
int zero = 0;//记录每个物品的重量(zero)
for (int j = 0; j < chars.length; j++) {
if(chars[j] == '1')one++;
if(chars[j] == '0')zero++;
}
for (int j = m; j >= zero; j--) {
for (int k = n; k >= one; k--) {
dp[j][k] = Math.max(dp[j][k],dp[j-zero][k-one]+1);
}
}
}
return dp[m][n];
}
}0-1背包问题变形(取与不取、分为两堆问题)
取与不取问题如果用回溯算法,则是指数级别的,用动态规划则是o(n方)
每个元素都有选择和不选择两种情况,然后尽可能分成两堆,两堆价值相同

判断条件:dp[half]==half
java
for(int i = 0;i< nums.size();i++){
for(int j = half;j>=nums[i];j--){
dp[j] = Math.max(dp[j],dp[j-nums[i]]+nums[i]);
}
}
判断条件:(sum-dp[half])-dp[half]

分为left(正数集合)和right(负数集合),left+right = target,left-right = sum
推出left = (target+sum)/2
该题可以转化为背包问题:当背包容量为left时有几种方法?dp不再为之前的价值,而是达到背包条件的方法数 dp[j] += dp[j-nums[i]]
例如:dp[j],j 为5, 已经有⼀个1(nums[i]) 的话,有 dp[4]种⽅法 凑成 容量为5的背包。 已经有⼀个2(nums[i]) 的话,有 dp[3]种⽅法 凑成 容量为5的背包。 已经有⼀个3(nums[i]) 的话,有 dp[2]中⽅法 凑成 容量为5的背包 已经有⼀个4(nums[i]) 的话,有 dp[1]中⽅法 凑成 容量为5的背包 已经有⼀个5 (nums[i])的话,有 dp[0]中⽅法 凑成 容量为5的背包
判断条件:return dp[left]
2.2 完全背包问题(可重复选)
模板:
java
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}组合问题/排列问题:

本题和纯完全背包不⼀样,纯完全背包是凑成背包最⼤价值是多少,⽽本题是要求凑成总⾦额的物品组合个数
java
确定递推公式
dp[j] 就是所有的dp[j - coins[i]](考虑coins[i]的情况)相加。
所以递推公式:dp[j] += dp[j - coins[i]]dp初始化:dp[0] = 1,如果为0,则所有为0
组合:
java
for (int i = 0; i < coins.size(); i++) { // 遍历物品
for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量
dp[j] += dp[j - coins[i]];
}
}排列(把组合的物品和背包顺序颠倒):
java
for (int j = 0; j <= amount; j++) { // 遍历背包容量
for (int i = 0; i < coins.size(); i++) { // 遍历物品
if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
}
}最值

java
static public int coinChange(int[] coins, int amount) {
int num = 0;
int dp[] = new int[amount+1];
for (int i = 1; i <= amount; i++) {
int min = Integer.MAX_VALUE;
for (int j = 0; j < coins.length; j++) {
//需要dp[i-coins[j]]!=Integer.MAX_VALUE这个条件,因为如果不加,可能会越界,变成负数
if(i>=coins[j] && dp[i-coins[j]]!=Integer.MAX_VALUE){
dp[coins[j]] = 1;
min = Math.min(dp[i-coins[j]]+1, min);
}
}
dp[i] = min;
}
if( dp[amount]==Integer.MAX_VALUE)return -1;
return dp[amount];
}
法一:
java
class Solution {
static public boolean wordBreak(String s, List<String> wordDict) {
String dp[] = new String[s.length()+1];
//需要初始化为空串
for (int j = 0; j <= s.length(); j++) {
dp[j] = "";
}
//用排列,因为组合会错过之前的单词
for (int j = 0; j <= s.length() ; j++) {
for (int i = 0; i < wordDict.size(); i++) {
if(j>=wordDict.get(i).length() ){
String tmp = s.substring(0, j);
if(dp[j].equals(tmp)){//不选择第i个单词,
dp[j] = dp[j];
}
else{//选择第i个单词
dp[j] = dp[j-wordDict.get(i).length()]+wordDict.get(i);
}
}
}
}
if(dp[s.length()].equals(s))
return true;
return false;
}
}法二: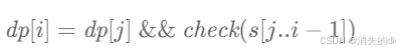
java
public class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
Set<String> wordDictSet = new HashSet(wordDict);
boolean[] dp = new boolean[s.length() + 1];
dp[0] = true;
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i; j++) {
if (dp[j] && wordDictSet.contains(s.substring(j, i))) {
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}
}2.3 树形dp
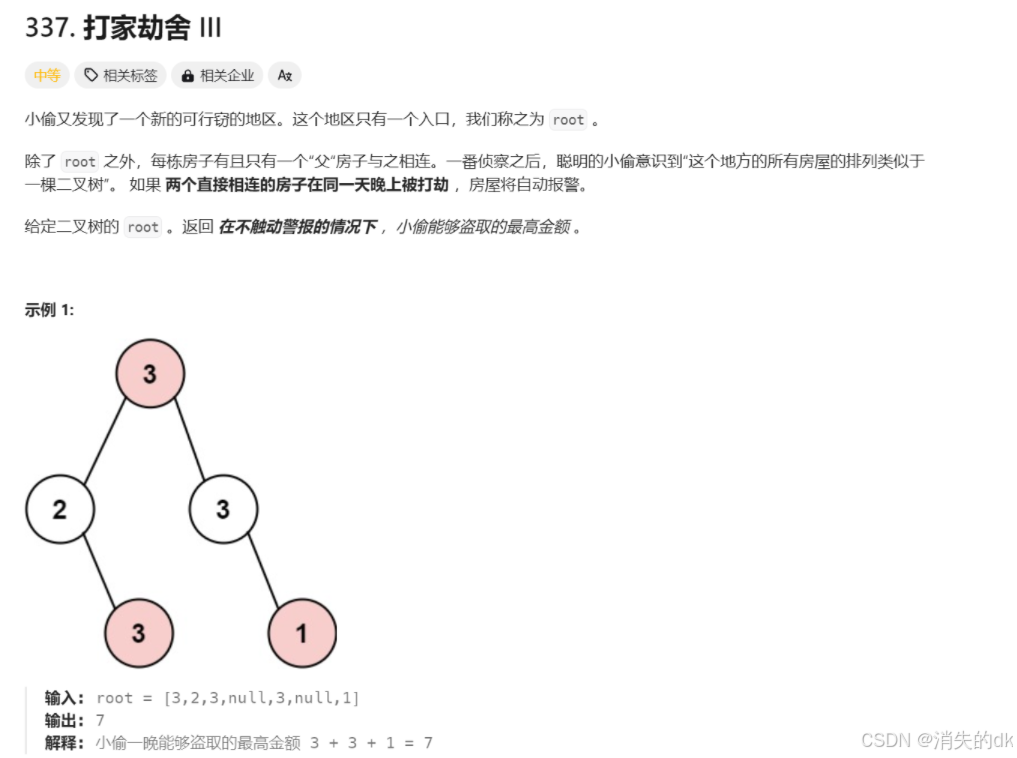
解法一:暴力递归
4 个孙子偷的钱 + 爷爷的钱 VS 两个儿子偷的钱 哪个组合钱多,就当做当前节点能偷的最大钱数。这就是动态规划里面的最优子结构
java
class Solution {
static public int rob(TreeNode root) {
if(root == null) return 0;
int money = root.val;
if(root.left!=null){
money+=rob(root.left.left);
money+=rob(root.left.right);
}
if(root.right!=null){
money+=rob(root.right.left);
money+=rob(root.right.right);
}
return Math.max(money,rob(root.right)+rob(root.left));
}
}解法二:使用HashMap记忆化
java
class Solution {
static public int rob(TreeNode root) {
HashMap<TreeNode,Integer>map = new HashMap<>();
return robMap(root,map);
}
static public int robMap(TreeNode root,HashMap<TreeNode,Integer>map) {
if(root == null) return 0;
if(map.containsKey(root)){
return map.get(root);
}
int money = root.val;
if(root.left!=null){
money+=robMap(root.left.left,map);
money+=robMap(root.left.right,map);
}
if(root.right!=null){
money+=robMap(root.right.left,map);
money+=robMap(root.right.right,map);
}
map.put(root,Math.max(money,robMap(root.right,map)+robMap(root.left,map)));
return Math.max(money,robMap(root.right,map)+robMap(root.left,map));
}
}⭐解法三:动态规划
每个节点可选择偷或者不偷两种状态,根据题目意思,相连节点不能一起偷
当前节点选择偷时,那么两个孩子节点就不能选择偷了 当前节点选择不偷时,两个孩子节点只需要拿最多的钱出来就行(两个孩子节点偷不偷没关系) 我们使用一个大小为 2 的数组来表示 int[] res = new int[2] 0 代表不偷,1 代表偷 任何一个节点能偷到的最大钱的状态可以定义为 当前节点选择不偷:当前节点能偷到的最大钱数 = 左孩子能偷到的钱 + 右孩子能偷到的钱 当前节点选择偷:当前节点能偷到的最大钱数 = 左孩子选择自己不偷时能得到的钱 + 右孩子选择不偷时能得到的钱 + 当前节点的钱数
java
public int rob(TreeNode root) {
int[] result = robInternal(root);
return Math.max(result[0], result[1]);
}
public int[] robInternal(TreeNode root) {
if (root == null) return new int[2];
int[] result = new int[2];
int[] left = robInternal(root.left);
int[] right = robInternal(root.right);
result[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
result[1] = left[0] + right[0] + root.val;
return result;
}解法二(记忆化回溯)每个节点回溯两次,只不过第二次回溯通过哈希表进行实现,而解法三,每个节点回溯仅回溯一边,回溯返回的是两个值【偷,不偷】
2.4 买卖股票问题
只能买卖股票一次(每一次的买的时候,都是初始值都是0)

1、确定dp数组以及下标的含义 每天其实就是两种状态,手里有股票和手里没股票,再加上"某天"这个维度,所以用一个二维的就可以表示所有天数的情况。dp数组有i行,i就是天数。有两列,表示某一天的两种情况。 dp【i】【0】表示,第i天手里持有股票的状态(这里持有的这个股票有两种情况,一是前面一直没买过股票,买了第i天这个股票,也可能是第i天之前的某一天已经买了一个股票,一直没卖,然后一直持有到第i天),能有的最多利润 dp【i】【1】表示,第i天手里不持有股票状态(这里的不持有股票有三种情况,一是从第0天到第i天,一直没买过股票,二是第i天之前的某一天买过股票,我们在第i天卖掉,三是在第i天之前已经有过一次买股票和一次卖股票的操作了所以在第i天是不持有股票的状态),能有的最多的利润
2、递推公式 dp【i】【0】 = max(dp【i-1】【0】,-prices【i】) 前面说过,持有股票有两种情况,如果是之前就有股票,那么就是dp【i-1】【0】,如果之前一直没买股票,然后买了第i天这个股票,那么我们的利润应该是-prices【i】,为什么不是dp【i-1】【1】-prices【i】?从两个方面都可以解释,一方面,本题只能买股票一次,如果我们选择第i天买这个股票,那么我们第i天之前应该是买不了股票,更加卖不了股票,也就是说什么操作都不做。那么我们的利润应该一直都是0,所以当我们第i天买这个股票时,我们的利润变成了-prices【i】。第二个方面,我们前面已经解释过了不持有股票的状态,有三种情况。而想用dp【i-1】【1】-prices【i】的同学是想用这三种情况中的第一种情况。
dp【i】【1】 = max(dp【i-1】【1】, dp【i-1】【0】+prices【i】) 前面说过,不持有股票有三种情况,但是第一种情况(一直没买过股票)和第三种情况(第i天之前已经进行过一次买卖股票的操作)都可以用dp【i-1】【1】表示,第二种情况就是第i天之前买过,我们在第i天卖掉,所以就是dp【i-1】【0】+prices【i】
买卖股票可以多次(每次买股票前的初始值为dp[i-1] [1])

java
public int maxProfit(int[] prices) {
int [][]dp = new int[prices.length][2];
dp[0][0] = -prices[0];
for (int i = 1; i < dp.length; i++) {
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]-prices[i]);
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]+prices[i]);
}
return dp[prices.length-1][1];
}买卖股票至多两次(把两次会发生的状态都定义了)

java
public int maxProfit(int[] prices) {
int dp[][] = new int[prices.length][4];
dp[0][0] = -prices[0];
dp[0][1] = 0;
dp[0][2] = -prices[0];
dp[0][3] = 0;
for (int i = 1; i < prices.length; i++) {
dp[i][0] = Math.max(dp[i-1][0],-prices[i]);
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]+prices[i]);
dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1]-prices[i]);
dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2]+prices[i]);
}
return dp[prices.length-1][3];
}冷冻期
java
static public int maxProfit( int[] prices) {
if(prices.length==1 || prices.length==0)return 0;
int dp[][] = new int[prices.length][2];
dp[0][0] = -prices[0];
dp[1][0] = Math.max(dp[0][0],dp[0][1]-prices[1]);
dp[1][1] = Math.max(dp[1][0],dp[1][0]+prices[1]);
for (int i = 2; i < dp.length; i++) {
//买股需要本金是两天前的卖出去的股的钱,为什么可以用两天前的表示,因为前一天冷冻期,不可能卖出,只有卖出dp[i-1][1]!=dp[i-2][1],所以需要加上冷冻期这个条件后,就是两天前的
dp[i][0] = Math.max(dp[i-1][0],dp[i-2][1]-prices[i]);
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]+prices[i]);
}
return dp[prices.length-1][1];
}2.5 子序列

递推公式:
dp[i] = Math.max(dp[i],dp[j]+1);
java
static public int lengthOfLIS(int[] nums) {
int dp[] = new int[nums.length];
for (int i = 0; i < dp.length; i++) {
dp[i] = 1;
}
for (int i = 1; i < dp.length; i++) {
for (int j = 0; j < i; j++) {
if(nums[i]>nums[j]){
dp[i] = Math.max(dp[i],dp[j]+1);
}
}
}
//这里最大值不是dp[nums.size()-1],因为最大递增序列不一定是以最后一个结尾,所以需要遍历每个元素,以每个
int max = 0;
for (int i = 0; i < dp.length; i++) {
max = Math.max(dp[i],max);
}
return max;
}如果有两个数组需要比较,就用二维dp数组

关键:二维dp数组
java
static public int findLength(int[] nums1, int[] nums2) {
int dp[][] = new int[nums1.length+1][nums2.length+1];
int result = 0;
for (int i = 1; i <=nums1.length ; i++) {
for (int j = 1; j <=nums2.length ; j++) {
//dp公式:
if(nums1[i-1]==nums2[j-1]){
dp[i][j] = dp[i-1][j-1]+1;
}
/
if(dp[i][j]>result)result = dp[i][j];
}
}
return result;
}
注意:这里的dp[i]不是前i项的最大和,而是包括第i项的最大和,因为就两种情况,一种是连着前面的dp[i-1]+nums[i],另一种是前面的断开,自己从头开始nums[i];
java
static public int maxSubArray(int[] nums) {
if(nums.length==1)return nums[0];
int dp[] = new int[nums.length];
dp[0] = nums[0];
int max = dp[0];
for (int i = 1; i < nums.length; i++) {
//d
dp[i]= Math.max(dp[i-1]+nums[i],nums[i]);
if(dp[i]>max)max = dp[i];
}
return max;
}
dp[i] [j]含义:在[0,i-1]和[0,j-1]的最小删除步数
递推公式:
java
if(t.charAt(i-1)==s.charAt(j-1)){
dp[i][j] = dp[i-1][j-1];
}
else dp[i][j] = Math.min(dp[i-1][j]+1,Math.min(dp[i][j-1]+1,dp[i-1][j-1]+2));
java
class Solution {
static public int minDistance(String s, String t) {
int dp[][] = new int[t.length()+1][s.length()+1];
for (int i = 0; i <= t.length(); i++) {
dp[i][0] = i;
}
for (int j = 0; j <= s.length(); j++) {
dp[0][j] = j;
}
dp[0][0] = 0;
for (int i = 1; i <= t.length(); i++) {
for (int j = 1; j <= s.length(); j++) {
if(t.charAt(i-1)==s.charAt(j-1)){
dp[i][j] = dp[i-1][j-1];
}
else dp[i][j] = Math.min(dp[i-1][j]+1,Math.min(dp[i][j-1]+1,dp[i-1][j-1]+2));
}
}
return dp[t.length()][s.length()];
}
}另外一个做法:先求出公共子序列,再减去剩余的数

唯一与上一题不同的是,加了插入和替换,插入与删除同样的操作,替换为dp[i] [j] = dp[i-1] [j-1]+1
java
static public int minDistance(String s, String t) {
int dp[][] = new int[t.length()+1][s.length()+1];
for (int i = 0; i <= t.length(); i++) {
dp[i][0] = i;
}
for (int j = 0; j <= s.length(); j++) {
dp[0][j] = j;
}
dp[0][0] = 0;
for (int i = 1; i <= t.length(); i++) {
for (int j = 1; j <= s.length(); j++) {
if(t.charAt(i-1)==s.charAt(j-1)){
dp[i][j] = dp[i-1][j-1];
}
else dp[i][j] = Math.min(dp[i-1][j]+1,Math.min(dp[i][j-1]+1,dp[i-1][j-1]+1));
}
}
return dp[t.length()][s.length()];
}
dp[i] [j]为 s[i] 到 s[j] 序列的最长回文子序列
例如:abca
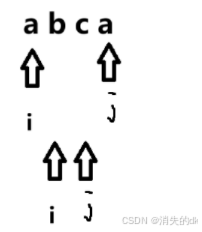
递推公式: if(s[i] == s[j]) dp[i] [j] = dp[i+1] [j-1]+2; else Math.max(dp[i+1] [j],dp[i] [j-1])
初始化:最初开始的是从单个字母开始,dp[i] [i] = 1,然后i和j分别往两边扩散
遍历顺序:从下往上,从左往右

java
public int longestPalindromeSubseq(String s) {
int dp[][] = new int[s.length()][s.length()];
for (int i = 0; i < s.length(); i++) {
dp[i][i] = 1;
}
for (int i = s.length()-1; i >= 0 ; i--) {
for (int j = i+1; j < s.length(); j++) {
if(s.charAt(i)==s.charAt(j)){
dp[i][j] = dp[i+1][j-1]+2;
}
else{
dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]);
}
}
}
return dp[0][s.length()-1];
}