西湖大学赵世钰老师的强化学习的数学原理课程(B站)学习笔记
第一章 


包含两个方面的内容:第一部分是一些基本概念
第二部分在MDP框架下以更加正式的形式去介绍
本章核心:建立RL的基础概念体系,理解MDP的数学形式化

整节课会广泛运用的一个案例是网格世界
这个网格世界由不同的网格组成,有的可以进去、有的禁止进入、有的是目标网格,网格世界也有边界
这个案例非常容易理解和直观
状态空间:9个格子(s1s_1s1 到 s9s_9s9),其中 s1=(1,1)s_1=(1,1)s1=(1,1) 表示坐标
环境约束:边界(不可跨越)、禁止区域(陷阱)、目标区域(终点)
核心问题:如何定义"好"的路径?如何让智能体(Agent)自主找到最优策略?

接下来介绍整个课程的第一个概念,state
定义:智能体在环境中的当前位置/情况
数学表示:s∈Ss \in \mathcal{S}s∈S,网格世界中 S={s1,s2,...,s9}\mathcal{S} = \{s_1, s_2, ..., s_9\}S={s1,s2,...,s9}
注意:s1s_1s1 只是索引,实际对应物理世界的二维坐标 (1,1)(1,1)(1,1)

下一个概念是action
定义:在给定状态下可执行的操作
数学表示:a∈A(s)a \in \mathcal{A}(s)a∈A(s),强调动作空间依赖于状态(不同状态可用动作不同)
示例:在边界格子尝试"向上"可能无效或受惩罚
在每个状态实际上有一系列可以采取的行动
把所有的动作集合在一起就得到了动作空间 action space
动作集合是与状态集合相依赖的,也就是说不同状态的动作空间是不一样的

下一个概念是状态转移
当智能体采取了一个动作,智能体自身从一个状态移动到了另一个状态,这个过程就叫做状态转移,state transition
state transition实际上是定义了智能体与环境交互的一种行为
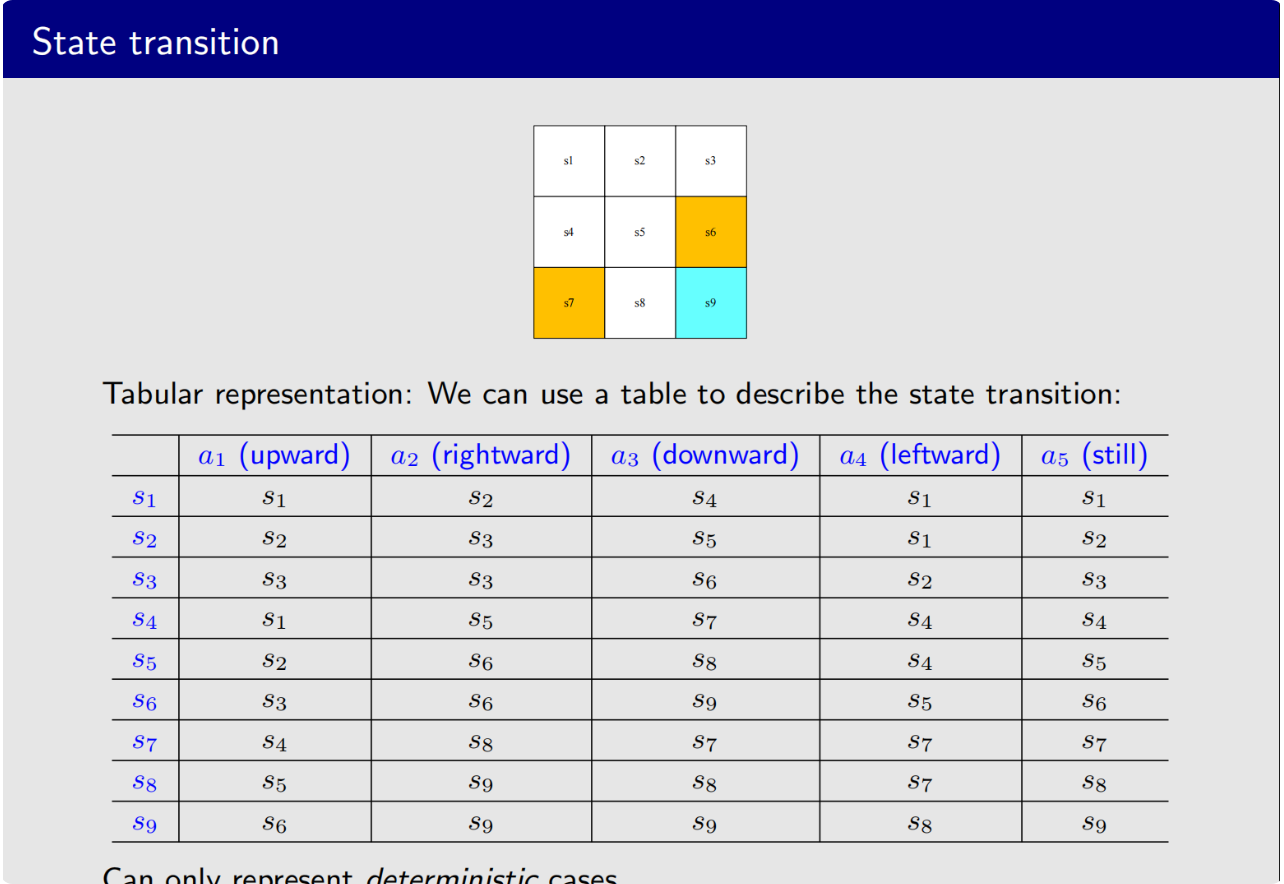
状态转移可以通过表格的形式表现出来,每一行是对应每一个状态,每一列对应了不同的动作,虽然表格是非常直观的,但是在实际过程中使用非常受限,因为它只能表示确定性的情况

所以我们引入状态转移概率
这是条件概率,
p(s2∣s1,a2)=1p(si∣s1,a2)=0∀i≠2\begin{aligned}&p(s_2|s_1,a_2)=1\\&p(s_i|s_1,a_2)=0\quad\forall i\neq2\end{aligned}p(s2∣s1,a2)=1p(si∣s1,a2)=0∀i=2
p(s′∣s,a)=P(St+1=s′∣St=s,At=a)p(s'|s,a) = \mathbb{P}(S_{t+1}=s' | S_t=s, A_t=a)p(s′∣s,a)=P(St+1=s′∣St=s,At=a)
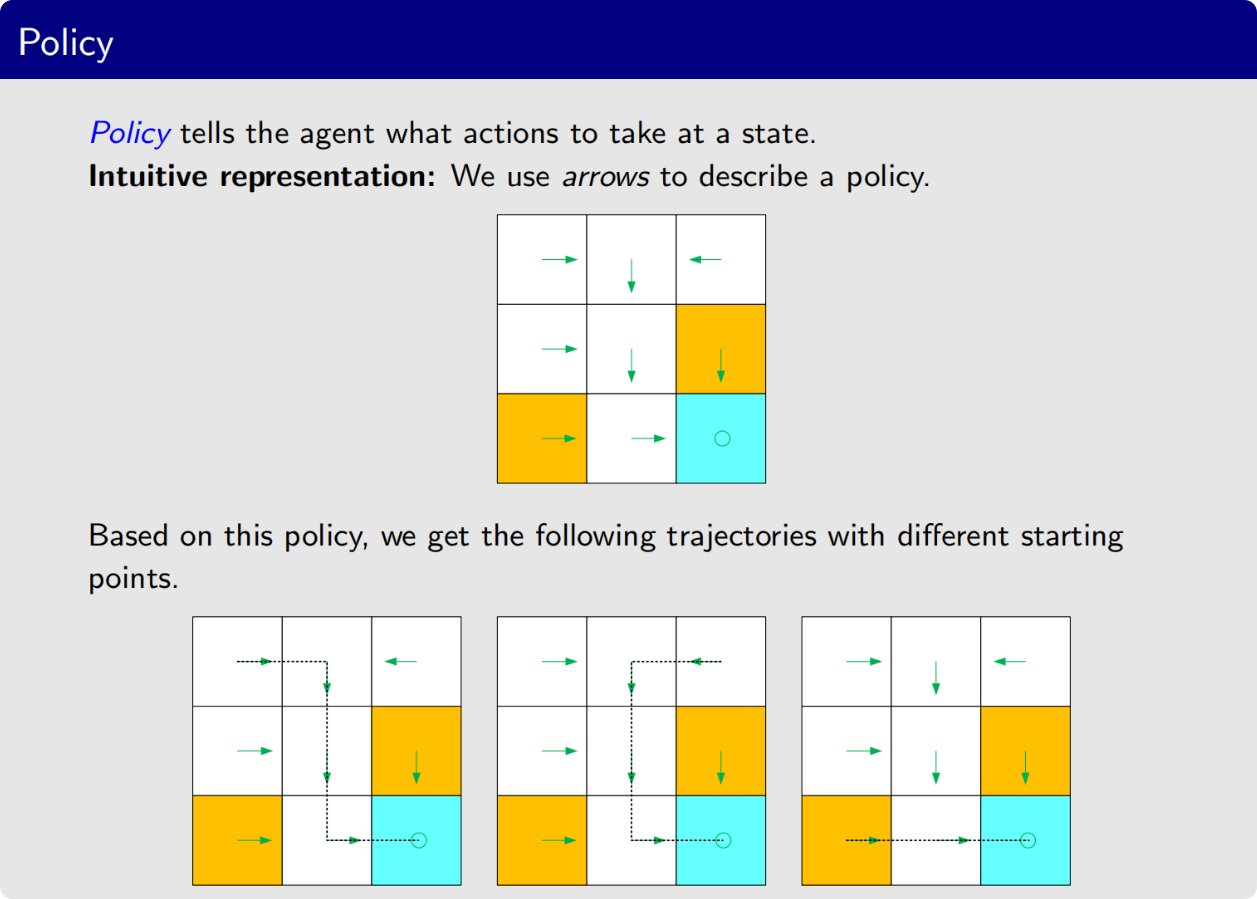
下面引入强化学习中一个非常重要而且是独有的概念
policy 策略
策略是状态到动作的映射,是RL的核心优化对象
它会告诉智能体,我处于某种状态下,我应该采取什么动作
基于这个策略,我们可以得到一些path或者说trajectory

实际过程中我们一般用条件概率来描述策略
比如针对s1s_1s1它的策略π\piπ
π(a5∣s1)=0\pi(a_5|s_1)=0π(a5∣s1)=0
这就是一个策略


奖励Reward是强化学习当中非常有独特性的一个概念
首先它是一个实数,是一个标量,在agent采取了一个动作之后它会得到这样的一个数
如果这个数是正数,说明我们是对这个行动是鼓励的,如果是负数,说明我们不希望这个动作发生,实际上就是一种惩罚
这就带来了两个问题,第一是如果我们不给reward,或者说奖励设为0会怎么样?这个实际上就是没有惩罚,没有惩罚,其实也是一种鼓励
第二就是我们能不能用正数代表惩罚,用负数代表鼓励?这其实是可以的,这是数学上的一种技巧,
在我们这个网格世界中,是这样设计奖励的:
如果智能体想要逃出四周的边界,奖励为-1
如果智能体想要进入禁止区域,奖励为-1
如果智能体到达了目标网格,奖励为+1
除此以外,智能体的奖励为0
奖励实际上可以理解为人机交互的界面,让人引导智能体告诉它应该怎么样做,不应该怎么样做,可以通过设计奖励来达到我们的目标
这种奖励是deterministic的,确定性的,但是实际上是不确定的,这个时候就需要使用条件概率
状态-动作-奖励这样的链就是轨迹
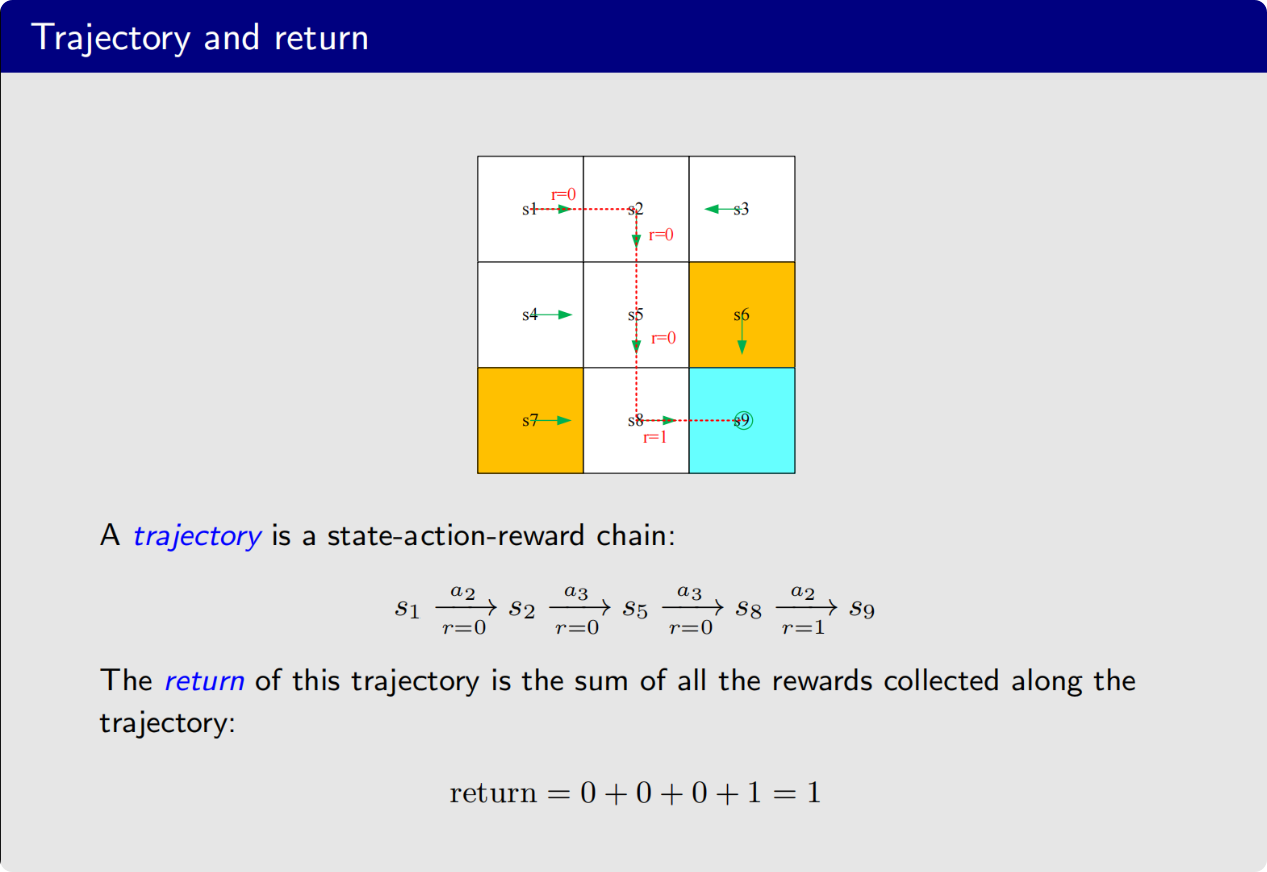
一个重要的概念,return,反馈,它是针对一个trajectory而言的(长期收益)
对于一条轨迹来说,它的return是沿着这个轨迹的全部奖励加起来得到的

非常重要的一个概念,discounted return
我们可以看一个例子,一个轨迹,到了目标之后它的策略还是持续地运行,会发散掉

这样我们就引入一个discounted rate
γ∈[0,1)\gamma \in[0,1)γ∈[0,1)
discounted rate和return结合就得到了discounted return
discountedreturn=0+γ0+γ20+γ31+γ41+γ51+...=γ3(1+γ+γ2+...)=γ311−γ.\begin{aligned}discountedreturn&=0+\gamma0+\gamma^{2}0+\gamma^{3}1+\gamma^{4}1+\gamma^{5}1+\ldots\\&=\gamma^3(1+\gamma+\gamma^2+\ldots)=\gamma^3\frac{1}{1-\gamma}.\end{aligned}discountedreturn=0+γ0+γ20+γ31+γ41+γ51+...=γ3(1+γ+γ2+...)=γ31−γ1.
我们通过引入discounted return得到了一个有限的值,能够平衡更远的未来的reward和更近的当前的reward之间的关系
减小γ\gammaγ能让它更加的近视,也就是会注重最近的一些reward
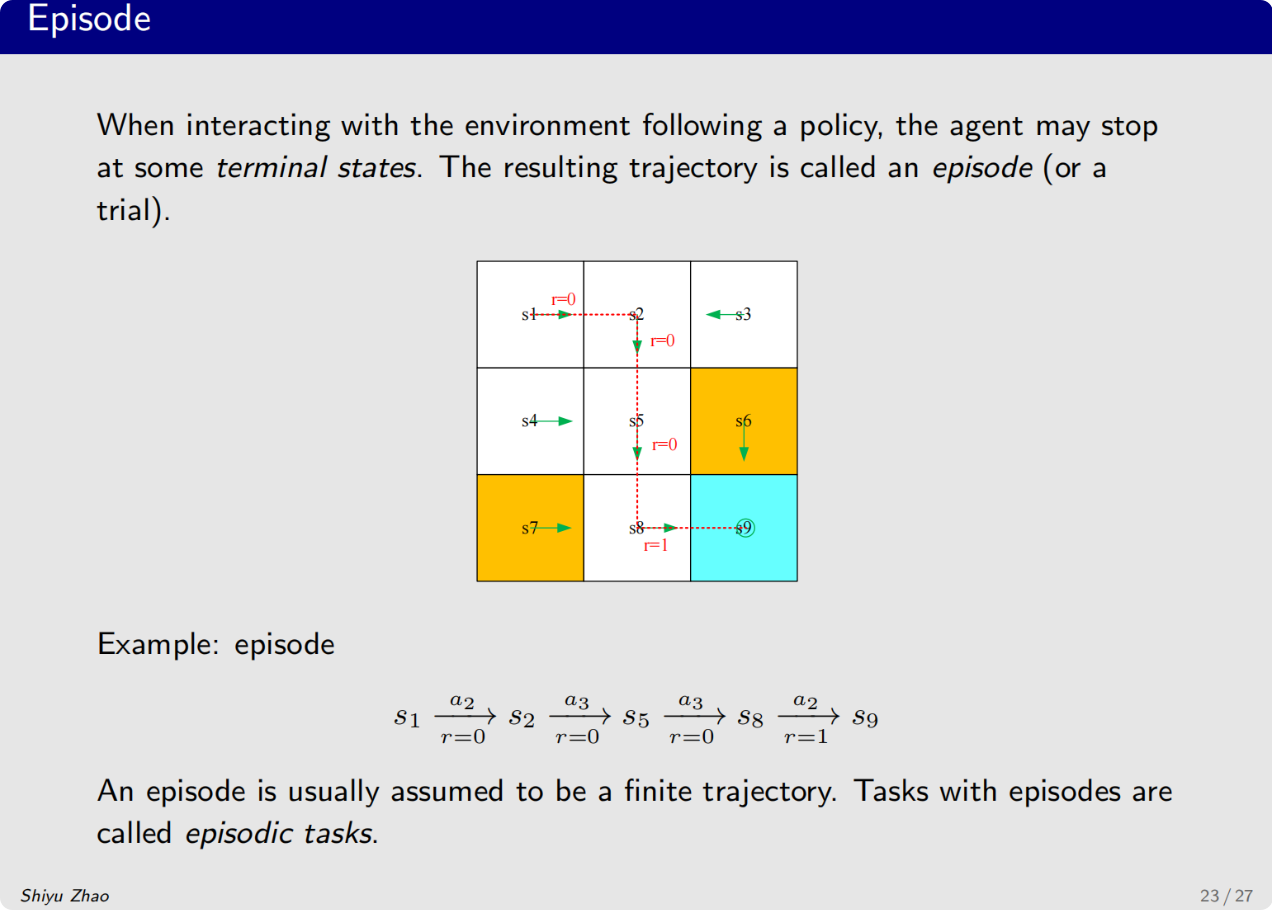
下一个重要的概念是episode回合
首先episode会伴随一个叫terminal state的
就是我从s1出发,最后到s9的时候,轨迹实际上已经停了
一个episode通常都是有限步的
有些任务实际上是没有终止状态的,这意味着智能体和环境的交互会永远的持续下去,这种任务就成为了continuing tasks
现实生活中,其实没有这样的任务,但是在一个长周期的环境中,我们可以把一些任务看成是这样的,例如:股票交易、机器人持续控制
下面我们把这些概念放在MDP的框架中再正式介绍一遍

MDP七元组:(S,A,P,R,γ,ρ0,T)(\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma, \rho_0, T)(S,A,P,R,γ,ρ0,T)
状态集合
动作集合
奖励集合
状态转移概率
奖励概率
策略
马尔可夫性(Markov Property):
p(st+1∣st,at)=p(st+1∣st,at,st−1,at−1,...)p(s_{t+1}|s_t, a_t) = p(s_{t+1}|s_t, a_t, s_{t-1}, a_{t-1}, ...)p(st+1∣st,at)=p(st+1∣st,at,st−1,at−1,...)
即:未来只依赖于当前状态,与历史无关(无记忆性)。
可以用这三个关键词来描述MDP
Markov:首先它对应了马尔科夫属性,
decision process:对应了策略
process:从什么状态跳到什么状态
关键理解:
- Policy 是智能体的"大脑"(决策函数)
- Reward 是环境的"反馈"(指导信号)
- Return 是评估策略优劣的"标准"
- MDP 是描述交互的"数学语言"
- 奖励设计的艺术性:RL的成败往往取决于奖励函数设计,它是人机交互的主要接口
- 折扣因子的意义:不仅解决数学收敛问题,更体现"时间偏好"(Time Preference)
- 马尔可夫性的假设:实际应用中若历史信息重要,可通过扩展状态空间(如使用RNN)来满足
- 随机性的必要性:随机策略(Stochastic Policy)在探索和多智能体场景中往往优于确定性策略
参考资料
- 《强化学习的数学原理》(赵世钰)
- Sutton & Barto《Reinforcement Learning: An Introduction》第3章