【生信绘图】基因组大小与CDS数量关系的可视化

引言

在基因组学研究中，一个基本问题是：基因组大小与编码基因（CDS）数量之间存在怎样的关系？ 不同来源的基因组------如单细胞基因组（SAG）、宏基因组组装基因组（MAG）和完整测序基因组（WGS）------可能表现出不同的标度律。为了直观地探索这种关系，我们常常需要将数据可视化，并辅以统计检验。

本文分享一段完整的Python代码，它能够：

• 读取或模拟基因组大小与CDS数量的数据；
• 在对数空间进行线性拟合，计算各组样本的残差；
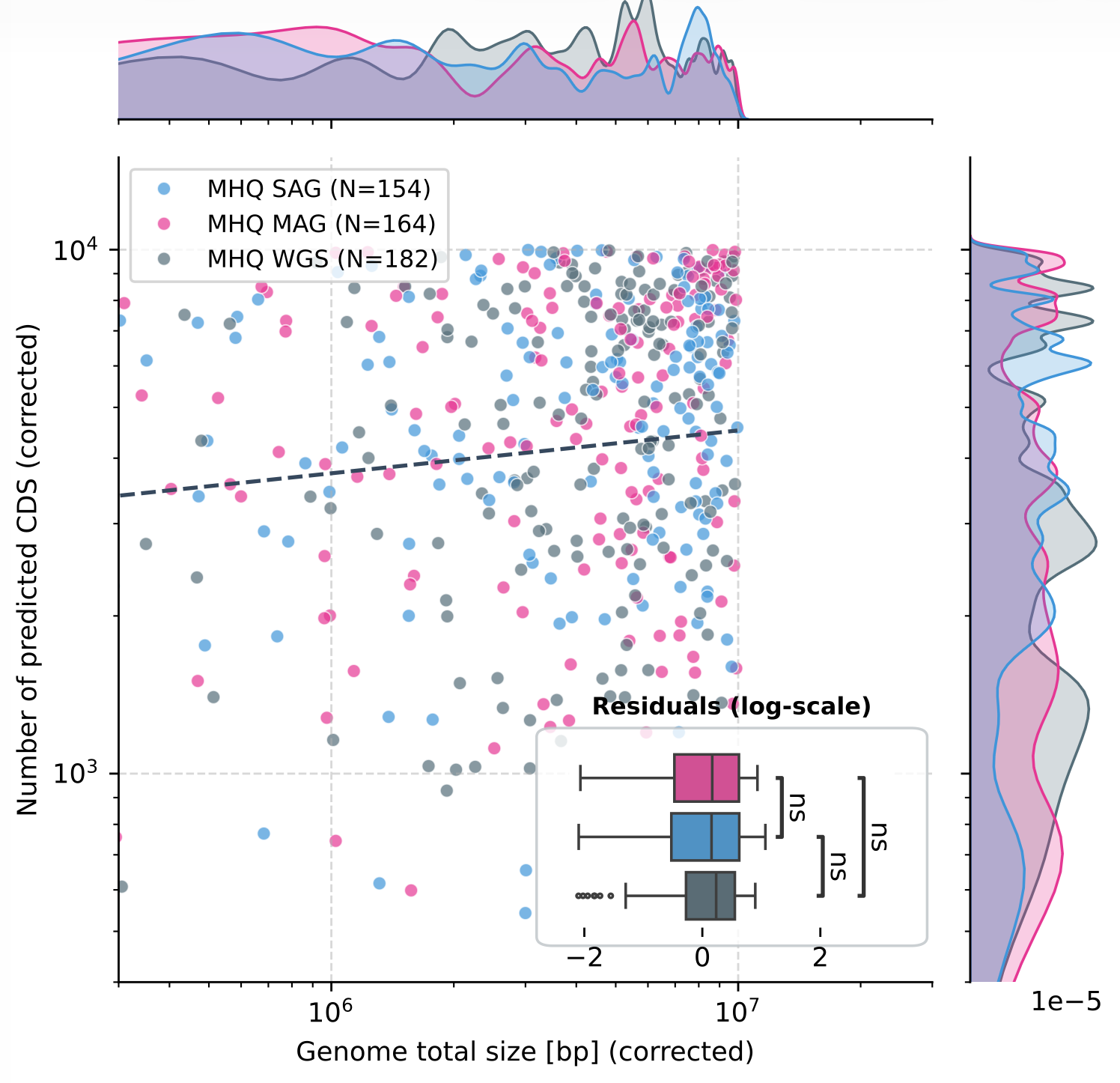
• 绘制联合分布图（散点图 + 边缘密度），并叠加回归线；
• 在主图中嵌入一个残差箱线图，比较不同基因组类型偏离总体趋势的程度；
• 自动添加统计显著性标注（Mann‑Whitney U检验）。
• 最终输出一张信息丰富、可直接用于出版的矢量图（PDF）。所有参数集中配置，方便修改和复用。
  

1. 数据准备与预处理

1.1 数据来源

代码支持两种数据来源：

• 真实数据：从 data.csv 读取，要求包含 length（基因组长度）、number_of_cds（CDS数量）和 type（SAG/MAG/WGS）三列。
• 模拟数据：若文件不存在，自动生成500个样本，用于测试。

1.2 对数变换与线性拟合

生物学数据常遵循幂律分布y=a⋅xby= a \cdot x^by=a⋅xb，取对数后变为线性关系：
log(CDS)=b⋅log(length)+log(a)log(CDS)=b⋅log(length)+log(a)log(CDS)=b⋅log(length)+log(a)

我们使用 scipy.optimize.curve_fit 对全体数据（不分类型）进行最小二乘拟合，得到斜率bbb和截距log(a)log(a)log(a)。这一趋势线代表了基因组大小与CDS数量的总体关系。

1.3 残差计算

残差定义为实际值的对数与拟合值的对数之差：
residual=log(CDSobs)−log(CDSfit)residual=log(CDS_{obs} )−log(CDS_{fit})residual=log(CDSobs)−log(CDSfit)

正值表示该基因组比总体趋势预测的CDS更多，负值则更少。后续通过比较不同组的残差，可以判断哪类基因组系统性偏离总体趋势。

# 核心拟合代码
def linear_func(x, a, b):
    return a * x + b

log_len = np.log(df["length"])
log_cds = np.log(df["number_of_cds"])
popt, _ = sciopt.curve_fit(linear_func, log_len, log_cds)

df["residuals_log"] = log_cds - linear_func(log_len, *popt)

2. 主图：联合分布散点图 + 边缘密度

我们使用 seaborn.jointplot 绘制主图，它能同时展示散点分布和两个变量的边缘密度分布。

2.1 散点图设置

• 横轴为基因组大小（length），纵轴为CDS数量（number_of_cds），双对数坐标。
• 颜色按 type 区分，使用自定义调色板（蓝-粉-灰）。
• 散点添加白色边缘，增强可读性。

2.2 回归线

将拟合得到的幂律曲线绘制在原始坐标空间：
CDSfit=eb⋅log(length)+log(a)CDS_{fit} =e^{b⋅log(length)+log(a)}CDSfit=eb⋅log(length)+log(a)

2.3 边缘密度

通过 marginal_kws 控制核密度估计的带宽和填充，让分布形态一目了然。

2.4 图例增强

自动计算每类样本的数量，在图例中显示为 MHQ SAG (N=123) 形式，便于读者了解样本量。

g = sns.jointplot(data=df, x="length", y="number_of_cds", hue="type",
                  kind="scatter", alpha=0.7, height=6,
                  palette=CONFIG["colors"],
                  joint_kws={"s": 25, "edgecolor": "w", ...},
                  marginal_kws={"bw_adjust": 0.2, "fill": True})

3. 内嵌箱线图：残差分布与显著性检验

为了在不占用额外空间的情况下展示组间差异，我们在主图右下角嵌入一个水平箱线图，用于比较三类样本的对数残差分布。

3.1 创建内嵌坐标轴

使用 mpl_toolkits.axes_grid1.inset_locator.inset_axes 在主图坐标轴内部开辟一个小区域，通过 bbox_to_anchor 精确定位。

3.2 绘制箱线图

• 横轴为残差值，纵轴为类型（WGS、MAG、SAG），水平方向绘制。
• 颜色顺序与主图一致：灰（WGS）、粉（MAG）、蓝（SAG）。
• 隐藏默认的刻度线和边框，使内嵌图更干净。

3.3 统计标注

使用 statannotations.Annotator 自动进行两两 Mann‑Whitney U 检验，并在图上添加星号表示显著性（* p<0.05, ** p<0.01, *** p<0.001）。

3.4 添加背景框

通过 FancyBboxPatch 绘制一个带圆角的半透明白色背景，让内嵌图从主图中突出。

ax_ins = inset_axes(g.ax_joint, width="40%", height="22%", loc="lower right", ...)
sns.boxplot(data=df, x="residuals_log", y="type", hue="type",
            order=["WGS", "MAG", "SAG"], palette=box_colors, ax=ax_ins)
annotator = Annotator(ax_ins, [("WGS","MAG"), ("WGS","SAG"), ("MAG","SAG")], ...)
annotator.configure(test="Mann-Whitney", text_format="star")
annotator.apply_and_annotate()

4. 完整代码

# ==========================================
# 全基因组规模 vs CDS 数量分析（完整脚本）
# ==========================================

import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
import scipy.optimize as sciopt
import seaborn as sns
from mpl_toolkits.axes_grid1.inset_locator import inset_axes
from statannotations.Annotator import Annotator
from matplotlib.patches import FancyBboxPatch

# ----------------------------------------------------------
# 1. 全局配置：在此修改参数，全局生效
# ----------------------------------------------------------
random.seed(10)
np.random.seed(10)

CONFIG = {
    "seed": 10,
    "input_file": "data.csv",          # 真实数据路径，不存在时自动生成模拟数据
    "colors": ["#3498db", "#e84393", "#546e7a"],   # 蓝, 粉, 灰
    "hue_order": ["SAG", "MAG", "WGS"],
    "plot_limits": {
        "xlim": (3e5, 3e7),            # 3e5 ~ 3e7 bp
        "ylim": (400, 15000),          # CDS 数量范围
        "xlabel": "Genome total size [bp] (corrected)",
        "ylabel": "Number of predicted CDS (corrected)"
    }
}

# ----------------------------------------------------------
# 2. 数据处理：读取 + 对数空间线性拟合 + 残差计算
# ----------------------------------------------------------
def prepare_data(file_path):
    """
    读取原始数据，进行对数空间的线性拟合，并计算残差。
    若文件不存在，则生成模拟数据用于测试。

    Parameters
    ----------
    file_path : str
        CSV 文件路径。

    Returns
    -------
    df : pandas.DataFrame
        包含原始数据、拟合值及对数残差的数据框。
    popt : numpy.ndarray
        拟合参数 [斜率, 截距]。
    """
    try:
        df = pd.read_csv(file_path, index_col=0)
        print(f"成功加载数据：{file_path}")
    except FileNotFoundError:
        print(f"文件 {file_path} 不存在，正在生成模拟数据（500个样本）...")
        data = {
            "length": np.random.uniform(1e5, 1e7, 500),
            "number_of_cds": np.random.uniform(500, 10000, 500),
            "type": np.random.choice(CONFIG["hue_order"], 500)
        }
        df = pd.DataFrame(data)

    # 对数转换------生物数据通常服从幂律分布
    log_length = np.log(df["length"])
    log_cds = np.log(df["number_of_cds"])

    # 线性模型：log(cds) = a * log(length) + b
    def linear_func(x, a, b):
        return a * x + b

    # 最小二乘拟合
    popt, _ = sciopt.curve_fit(linear_func, log_length, log_cds)

    # 计算拟合值及对数残差
    df["log_length"] = log_length
    df["log_cds"] = log_cds
    df["cds_fit"] = np.exp(linear_func(log_length, *popt))
    df["residuals_log"] = log_cds - np.log(df["cds_fit"])

    return df, popt

# ----------------------------------------------------------
# 3. 主绘图：联合分布散点图 + 边缘密度 + 回归线
# ----------------------------------------------------------
def plot_main_joint(df, popt):
    """
    绘制主图：联合分布散点图（对数坐标）+ 边缘密度 + 对数空间回归线。

    Parameters
    ----------
    df : pandas.DataFrame
        包含 'length', 'number_of_cds', 'type' 及对数残差的数据框。
    popt : numpy.ndarray
        拟合参数 [斜率, 截距]，用于绘制回归线。

    Returns
    -------
    g : seaborn.JointGrid
        JointGrid 对象，可继续添加子图或修改样式。
    """
    g = sns.jointplot(
        data=df,
        x="length", y="number_of_cds", hue="type",
        kind="scatter", alpha=0.7, height=6,
        palette=CONFIG["colors"],
        hue_order=CONFIG["hue_order"],
        joint_kws={"s": 25, "edgecolor": "w", "linewidth": 0.5},
        marginal_kws={"bw_adjust": 0.2, "fill": True}
    )

    # 消除顶部边缘图 Y 轴的科学计数法
    g.ax_marg_x.ticklabel_format(axis="y", style="plain")

    # 设置坐标轴为对数刻度，并应用全局绘图范围
    g.ax_joint.set(xscale="log", yscale="log", **CONFIG["plot_limits"])
    g.ax_joint.grid(True, which="major", linestyle="--", alpha=0.5, zorder=0)

    # 在原始坐标空间绘制回归线
    x_log_range = np.linspace(df["log_length"].min(), df["log_length"].max(), 100)
    x_range = np.exp(x_log_range)
    y_fit = np.exp(popt[0] * np.log(x_range) + popt[1])
    g.ax_joint.plot(x_range, y_fit, color="#34495e", linestyle="--", lw=1.5, zorder=5)

    # 图例：添加样本量 (N=xxx)
    type_counts = df["type"].value_counts()
    handles, labels = g.ax_joint.get_legend_handles_labels()
    new_labels = [
        f"MHQ {l} (N={type_counts.get(l, 0)})"
        for l in labels if l in type_counts
    ]
    g.ax_joint.legend(handles=handles, labels=new_labels,
                      loc="upper left", fontsize=9)

    return g

# ----------------------------------------------------------
# 4. 内嵌箱线图：残差分布 + 显著性标注
# ----------------------------------------------------------
def add_inset_boxplot(joint_grid, df):
    """
    嵌入水平箱线图，展示三类样本的对数残差分布，并添加显著性星号。
    """
    ax_ins = inset_axes(
        joint_grid.ax_joint,
        width="40%", height="22%",
        loc="lower right",
        bbox_to_anchor=(-0.03, 0.05, 1, 1),
        bbox_transform=joint_grid.ax_joint.transAxes
    )

    # 箱线图颜色顺序（与主图图例对应）
    box_colors = [
        CONFIG["colors"][2],  # WGS  -> 灰
        CONFIG["colors"][1],  # MAG  -> 粉
        CONFIG["colors"][0]   # SAG  -> 蓝
    ]

    # ----- 专用于 sns.boxplot 的参数（含 hue + legend=False）-----
    box_plot_kws = {
        "data": df,
        "x": "residuals_log",
        "y": "type",
        "hue": "type",               # 新增，消除 FutureWarning
        "orient": "h",
        "order": ["WGS", "MAG", "SAG"],
        "palette": box_colors,
        "linewidth": 1,
        "fliersize": 1.5,
        "legend": False             # 避免自动生成多余图例
    }

    # 绘制箱线图
    sns.boxplot(**box_plot_kws, ax=ax_ins)

    # ----- 专用于 Annotator 的参数（去除 legend 等无关项）-----
    annotator_kws = {
        "data": df,
        "x": "residuals_log",
        "y": "type",
        "hue": "type",              # 保持一致，使颜色对应
        "orient": "h",
        "order": ["WGS", "MAG", "SAG"],
        "palette": box_colors       # Annotator 也会使用该配色
    }

    pairs = [("WGS", "MAG"), ("WGS", "SAG"), ("MAG", "SAG")]
    annotator = Annotator(ax_ins, pairs, **annotator_kws)
    annotator.configure(test="Mann-Whitney", text_format="star",
                        loc="inside", verbose=False)
    annotator.apply_and_annotate()

    # 后续样式设置（不变）
    ax_ins.set(xlabel=None, ylabel=None, yticks=[])
    ax_ins.set_title("Residuals (log-scale)",
                     fontsize=9, fontweight="bold", pad=12)
    for spine in ax_ins.spines.values():
        spine.set_visible(False)

    rect = FancyBboxPatch(
        (0, 0), 1, 1, transform=ax_ins.transAxes,
        facecolor="white", edgecolor="#bdc3c7", alpha=0.8,
        boxstyle="round,pad=0.1,rounding_size=0.05",
        clip_on=False, zorder=0
    )
    ax_ins.add_patch(rect)

# ----------------------------------------------------------
# 5. 主程序：执行完整分析流程
# ----------------------------------------------------------
if __name__ == "__main__":
    # 准备数据
    df, popt = prepare_data(CONFIG["input_file"])

    # 绘制联合分布主图
    g = plot_main_joint(df, popt)

    # 添加内嵌残差箱线图
    add_inset_boxplot(g, df)

    # 自动调整布局，防止标签重叠
    plt.tight_layout()

    # 保存为 PDF 文件（矢量格式，适合出版）
    output_file = "genome_size_vs_cds.pdf"
    plt.savefig(output_file, dpi=300, bbox_inches="tight")
    print(f"图像已保存至：{output_file}")

    # 屏幕显示
    plt.show()

结语

本文展示了一套完整的基因组大小与CDS数量关系的分析流程，重点在于：

• 对数空间的线性建模与残差分析；
• 联合分布图与内嵌子图的巧妙组合；
• 统计显著性的自动标注。

这种方法不仅适用于基因组数据，还可推广到任何需要展示"全局趋势+组间差异"的场景。希望这段代码能帮助你高效产出高质量的科研图表。