Cut-Shortcut实现

I still …2026-02-20 10:07

Cut-Shortcut实现

文章发表于PLDI 23，具体参考无需上下文的上下文敏感指针分析。目前将代码从artifact docker中拷贝出来放到cut-shortcut分支下。

在指针分析入口PointerAnalysis::runAnalysis下如果指定CutShortcut方法，那么base solver替换为CutShortcutSolver，同时增加3个插件LocalFlowHandler、FieldAccessHandler、ContainerAccessHandler分别处理local-flow、field-access、container-access 3种cut-flow。

1.算法原理

Cut-Shortcut的核心是尽量将callee -> callsite的value-flow转化为callsite -> callsite的value-flow，提高callsite中相关变量的指针分析精度同时callee的指向集并没有改变。比如下面示例中callee变量 p 1 p_1 p1 和 p 2 p_2 p2 的指向集调整后没变，但是两个caller变量 target 1 \text{target}_1 target1 和 target 2 \text{target}_2 target2 的指向集优化了。在Tai-e的分析过程中，通常会先增加 x → y x \rightarrow y x→y 的PFG Edge随后进行 pts ( x ) ⊆ pts ( y ) \text{pts}(x) \subseteq \text{pts}(y) pts(x)⊆pts(y) 的操作，因此Cut-shortcut的实现就是将callee -> callsite的PFG边替换为callsite -> callsite的PFG边。

原理上说Cut-Shortcut只是更改一些caller变量以及caller中分配的object的字段的指向集，对callee变量和callee分配的object字段的指向集不会修改。

在下面代码中:

  • c.setA(a) 的callee为 C::setA，其中有 this.a = a。则有 a → o . a ∈ PFG ∣ ∀ o ∈ pts ( this ) a \rightarrow o.a \in \text{PFG} \mid \forall o \in \text{pts}(\text{this}) a→o.a∈PFG∣∀o∈pts(this)，其中 a a a 为callee的形参， o . a o.a o.a 为caller中分配的object的字段。CutShortcut转化后为 a → o c . a a \rightarrow o_c.a a→oc.a。

  • a1 = c.getA() 中callee的代码为 return this.a，局部有 o . a → m r e t ∈ PFG ∣ ∀ o ∈ pts ( this ) o.a \rightarrow m_{ret} \in \text{PFG} \mid \forall o \in \text{pts}(\text{this}) o.a→mret∈PFG∣∀o∈pts(this)，而 o . a o.a o.a 为caller中分配的object的字段， m r e t m_{ret} mret 为callee返回的变量。CutShortcut转换后为 o c . a → a 1 o_c.a \rightarrow a_1 oc.a→a1。

java 复制代码 
C c = new C();// allocate oc
A a = new A();// allocate oa
c.setA(a);
A a1 = c.getA();

Cut-Shortcut基于context-insensitive规则做了下面调整，这里callee中的语句

  • l : x . f = y ∈ cutStores l: x.f = y \in \text{cutStores} l:x.f=y∈cutStores 满足 pts ( x ) \text{pts}(x) pts(x) 中的object o o o 都是在caller中分配的，正常规则会创建 y → o . f y \rightarrow o.f y→o.f 的PFG edge，属于callee -> caller的value-flow，需要打破。

  • m ret ∈ cutReturns m_{\text{ret}} \in \text{cutReturns} mret∈cutReturns 表示 pts ( m ret ) \text{pts}(m_{\text{ret}}) pts(mret) 全部来自caller，可以在各自caller中处理不用直接构造到callsite receiver的PFG边。

语句类型 示例 规则 说明
FieldLoad l : x . f = y l: x.f = y l:x.f=y y → o . f ∈ PFG ∣ l ∉ cutStores , ∀ o ∈ pts ( x ) y \rightarrow o.f \in \text{PFG} \mid l \notin \text{cutStores}, \forall o \in \text{pts}(x) y→o.f∈PFG∣l∈/cutStores,∀o∈pts(x) 如果处理的field store不属于cut store语句那么按照标准规则处理。这里cut stores包含3种情况，由3个plugin分别计算。
Call - Return l : x = v . k ( l a 1 , . . . , l a n ) l: x = v.k(l_{a_1}, ..., l_{a_n}) l:x=v.k(la1,...,lan) m ret → x ∈ PFG ∣ l → m ∈ CG , m ret ∉ cutReturns m_{\text{ret}} \rightarrow x \in \text{PFG} \mid l \rightarrow m \in \text{CG}, m_{\text{ret}} \notin \text{cutReturns} mret→x∈PFG∣l→m∈CG,mret∈/cutReturns 处理callee时，如果返回值 m ret m_{\text{ret}} mret 不在cut return集合中那么按照标准规则处理。cut return集合由3个plugin分别计算。

这里用 def ( x ) \text{def}(x) def(x) 表示定义了 x x x 的语句集合比如： x = . . . x = ... x=...。

1.1.Field Access

主要是处理 getter、setter 类情况，比如对于 x = y.getF()，更新之前有 load 边 Y . this . f → x Y.\text{this}.f \rightarrow x Y.this.f→x，随后有 o . f → x ∈ PFG ∣ ∀ o ∈ pts ( Y . this ) o.f \rightarrow x \in \text{PFG} \mid \forall o \in \text{pts}(Y.\text{this}) o.f→x∈PFG∣∀o∈pts(Y.this)，更新后这条 load 边应当被替换成 x = y.f，直接有 o . f → x ∈ PFG ∣ ∀ o ∈ pts ( y ) o.f \rightarrow x \in \text{PFG} \mid \forall o \in \text{pts}(y) o.f→x∈PFG∣∀o∈pts(y)。将callee -> callsite的value-flow替换为callsite -> callsite的value-flow。具体处理规则如下：

规则名称 处理规则 说明
[Arg2Var] l a k ↦ m p k ∣ l → m ∈ CG , def ( m p k ) = ∅ l_{a_k} \mapsto m_{p_k} \mid l \rightarrow m \in \text{CG}, \text{def}(m_{p_k}) = \empty lak↦mpk∣l→m∈CG,def(mpk)=∅ callee m m m 的参数没在 m m m 中被重新定义，那么存在data-flow关系 l a k ↦ m p k l_{a_k} \mapsto m_{p_k} lak↦mpk。对于 x ↦ y x \mapsto y x↦y， x x x 一定义callsite的参数， y y y 一定是callee的形参。
[CutStore] l a i ′ . f = l a j ′ ∈ tempStores , l ∈ cutStores ∣ l : m p i . f = m p j ∈ m , l a i ′ ↦ m p i , l a j ′ ↦ m p j l^{'}{a_i}.f = l^{'}{a_j} \in \text{tempStores}, l \in \text{cutStores} \mid l: m_{p_i}.f = m_{p_j} \in m, l^{'}{a_i} \mapsto m{p_i}, l^{'}{a_j} \mapsto m{p_j} lai′.f=laj′∈tempStores,l∈cutStores∣l:mpi.f=mpj∈m,lai′↦mpi,laj′↦mpj callee m m m 的参数 m p i m_{p_i} mpi 和 m p j m_{p_j} mpj 没有在 m m m 中被重新定义，那么 FieldStore l l l 在callsite中等价于 l a i ′ . f = l a j ′ l^{'}{a_i}.f = l^{'}{a_j} lai′.f=laj′，将 l l l 标记为temp store，同时指针分析中不处理 x . f = y x.f = y x.f=y，去除 m p j → o . f ∣ o ∈ pts ( m p i ) m_{p_j} \rightarrow o.f \mid o \in \text{pts}(m_{p_i}) mpj→o.f∣o∈pts(mpi) 的PFG边。
[PropStore] l a i ′ . f = l a j ′ ∈ tempStores ∣ l : m p i . f = m p j ∈ tempStores , l a i ′ ↦ m p i , l a j ′ ↦ m p j l^{'}{a_i}.f = l^{'}{a_j} \in \text{tempStores} \mid l: m_{p_i}.f = m_{p_j} \in \text{tempStores}, l^{'}{a_i} \mapsto m{p_i}, l^{'}{a_j} \mapsto m{p_j} lai′.f=laj′∈tempStores∣l:mpi.f=mpj∈tempStores,lai′↦mpi,laj′↦mpj callee m m m 中存在temp store m p i . f = m p j m_{p_i}.f = m_{p_j} mpi.f=mpj，其处理等价于其它store语句，这条语句主要是递归将temp store关系传递到caller中。
[ShortcutStore] y → o . f ∈ PFG ∣ x . f = y ∈ tempStores , o ∈ pts ( x ) , def ( x ) = ∅    ∨ def ( y ) = ∅    ∨ ∄ x = m p i ∨ ∄ y = m p j y \rightarrow o.f \in \text{PFG} \mid x.f = y \in \text{tempStores}, o \in \text{pts}(x), \text{def}(x) = \emptyset \; \vee \text{def}(y) = \emptyset \; \vee \not\exist x = m_{p_i} \vee \not\exist y = m_{p_j} y→o.f∈PFG∣x.f=y∈tempStores,o∈pts(x),def(x)=∅∨def(y)=∅∨∃x=mpi∨∃y=mpj def ( x ) = ∅    ∨ def ( y ) = ∅    ∨ ∄ x = m p i ∨ ∄ y = m p j \text{def}(x) = \emptyset \; \vee \text{def}(y) = \emptyset \; \vee \not\exist x = m_{p_i} \vee \not\exist y = m_{p_j} def(x)=∅∨def(y)=∅∨∃x=mpi∨∃y=mpj 表示temp store x . f = y x.f = y x.f=y 的关系不能再往caller中传播了，也就是只对top-level的 tempStores \text{tempStores} tempStores 更新PFG边。
[CutPropLoad] m ret ∈ cutReturns , r = l a i ′ . f ∈ tempLoads , o . f → m ret ∈ returnLoads ∣ l : m ret = m p i . f ∈ ( m ∪ tempLoads ) , l ′ : r = v . k ( l a 1 ′ , . . . ) , l a i ′ ↦ m p i , o ∈ pts ( m p i ) m_{\text{ret}} \in \text{cutReturns}, r = l^{'}{a_i}.f \in \text{tempLoads}, o.f \rightarrow m{\text{ret}} \in \text{returnLoads} \mid l: m_{\text{ret}} = m_{p_i}.f \in (m \cup \text{tempLoads}), l^{'}: r = v.k(l^{'}{a_1}, ...), l^{'}{a_i} \mapsto m_{p_i}, o \in \text{pts}(m_{p_i}) mret∈cutReturns,r=lai′.f∈tempLoads,o.f→mret∈returnLoads∣l:mret=mpi.f∈(m∪tempLoads),l′:r=v.k(la1′,...),lai′↦mpi,o∈pts(mpi) callee的返回值 m ret m_{\text{ret}} mret 可能从参数 l a i ′ l^{'}{a_i} lai′ 获取值，因此不将返回值往caller传播，而是等价于 r = l a i ′ . f r = l^{'}{a_i}.f r=lai′.f。
[ShortCutLoad] o . f → x ∈ PFG ∣ x = y . f ∈ tempLoads , o ∈ pts ( y ) o.f \rightarrow x \in \text{PFG} \mid x = y.f \in \text{tempLoads}, o \in \text{pts}(y) o.f→x∈PFG∣x=y.f∈tempLoads,o∈pts(y) 基于 tempLoads \text{tempLoads} tempLoads 构建shortcut PFG Edge
[RelayEdge] n → r ∈ PFG ∣ l : v . k ( . . . ) , l → m ∈ CG , m ret ∈ cutReturns , n → m ret ∈ PFG \ returnLoads n \rightarrow r \in \text{PFG} \mid l: v.k(...), l \rightarrow m \in \text{CG}, m_{\text{ret}} \in \text{cutReturns}, n \rightarrow m_{\text{ret}} \in \text{PFG} \backslash \text{returnLoads} n→r∈PFG∣l:v.k(...),l→m∈CG,mret∈cutReturns,n→mret∈PFG\returnLoads callee中可能存在 m ret = m p i . f m_{\text{ret}} = m_{p_i}.f mret=mpi.f 以及 m ret = n m_{\text{ret}} = n mret=n，将 m ret ∈ cutReturns m_{\text{ret}} \in \text{cutReturns} mret∈cutReturns 后，之前的规则没有处理 m ret = n m_{\text{ret}} = n mret=n，这里补充上。

这里涉及到一个概念：relay load，形式如 m ret = m p i . f m_{\text{ret}} = m_{p_i}.f mret=mpi.f，标准PFG更新是 o . f → m ret ∣ ∀ o ∈ pts ( m p i ) o.f \rightarrow m_{\text{ret}} \mid \forall o \in \text{pts}(m_{p_i}) o.f→mret∣∀o∈pts(mpi)，。但是 m ret m_{\text{ret}} mret 只要加载参数的值就会被加入到 cutReturns \text{cutReturns} cutReturns 中，根据 [ShortCutLoad] PFG更新规则为 o . f → r ∣ ∀ c , l : r = v . k ( . . . ) , l → m ∈ CG o.f \rightarrow r \mid \forall c, l: r = v.k(...), l \rightarrow m \in \text{CG} o.f→r∣∀c,l:r=v.k(...),l→m∈CG，但是如果有其它赋值关系 m ret = n m_{\text{ret}} = n mret=n， n n n 的值按照这个规则就同步不到caller中，[RelayEdge] 就是处理这个情况，这里 o . f → f o.f \rightarrow f o.f→f 属于 Non-Relay Edge，而 n → m ret n \rightarrow m_{\text{ret}} n→mret 属于 Relay Edge。分析时有 n → r ∈ PFG ∣ ∀ n → m ret ∈ RelayEdges n \rightarrow r \in \text{PFG} \mid \forall n \rightarrow m_{\text{ret}} \in \text{RelayEdges} n→r∈PFG∣∀n→mret∈RelayEdges。这样 n n n 和 m ret m_{\text{ret}} mret 的 pts \text{pts} pts 都没变，而caller变量 r r r 的 pts \text{pts} pts 精简了。

标准规则的PFG
relayEdge
n
m ret
r

Cut-Shortcut的PFG
relayEdge
n
m ret
r

1.2.Local Flow

主要针对下面这类pattern p 1 → r p_1 \rightarrow r p1→r 和 p 2 → r p_2 \rightarrow r p2→r，生成caller的local flow并去除callee的 m ret m_{\text{ret}} mret 到caller receiver的flow。

java 复制代码 
A select(A p1,A p2){
    A r;
    if (cond)
        r = p1;
    else
        r = p2;
    return r;
}

这里引入新的notation ⟨ m , k ⟩ ↣ x \langle m, k \rangle \rightarrowtail x ⟨m,k⟩↣x，表示 m m m 中的局部变量 x x x 与 m m m 的第 k k k 个parameter存在data-flow关系，并且这个data-flow path只有copy关系，没有field-load/store、array-load/store、call等其它关系，也就是不存在indirect-value flow，规则如下

规则名称 处理规则 说明
[Param2Var], [Param2VarRec] ⟨ m , k ⟩ ↣ m p k ∣ def ( m p k ) = ∅ \langle m, k \rangle \rightarrowtail m_{p_k} \mid \text{def}(m_{p_k}) = \emptyset ⟨m,k⟩↣mpk∣def(mpk)=∅ 生成初始fact
[Param2VarRec] ⟨ m , k ⟩ ↣ x ∣ ∀ l : x = y ∈ def ( x ) , ⟨ m , k ⟩ ↣ y \langle m, k \rangle \rightarrowtail x \mid \forall l: x = y \in \text{def}(x), \langle m, k \rangle \rightarrowtail y ⟨m,k⟩↣x∣∀l:x=y∈def(x),⟨m,k⟩↣y 如果对于所有定义 x x x 的语句 x = y x = y x=y 都有 ⟨ m , k ⟩ ↣ y \langle m, k \rangle \rightarrowtail y ⟨m,k⟩↣y，那么说明一定不存在其它indirect value flow重新定义 x x x，可以传递给 x x x。
[CutShortCutFlows] m ret ∈ cutReturns , l a k → r ∈ PFG ∣ l : r = v . k ( . . . ) , l → m ∈ CG , ⟨ m , k ⟩ ↣ m ret m_{\text{ret}} \in \text{cutReturns}, l_{a_k} \rightarrow r \in \text{PFG} \mid l: r = v.k(...), l \rightarrow m \in \text{CG}, \langle m, k \rangle \rightarrowtail m_{\text{ret}} mret∈cutReturns,lak→r∈PFG∣l:r=v.k(...),l→m∈CG,⟨m,k⟩↣mret 如果存在 ⟨ m , k ⟩ ↣ m ret \langle m, k \rangle \rightarrowtail m_{\text{ret}} ⟨m,k⟩↣mret，那么说明 m ret m_{\text{ret}} mret 的point-to set的值全部来自于caller。在caller中添加 l a k → r l_{a_k} \rightarrow r lak→r 的PFG Edge

1.3.Container Access

主要处理container使用，除了Cut-Shortcut，DBridge也实现了一个简单的容器访问分析机制，不过只对 Arrays.asList、List.add、Set.add、HashSet.add、List.iterator、Set.iterator、Iterable.iterator、Iterator.next 进行了建模。对于部分语句将container API调用转化为Array访问随后用Array的规则进行处理，对于 Collection.iterator 调用 i = v . iter i = v.\text{iter} i=v.iter，直接添加PFG边 ⟨ c , v ⟩ → ⟨ c , i ⟩ \langle c, v \rangle \rightarrow \langle c, i \rangle ⟨c,v⟩→⟨c,i⟩。这个机制足够简单方便维护不过很多API比如 LinkList.peekFirst 没处理，同时 Map 也没处理。

Container操作类型 语句 等价语句
List.add、Set.add、HashSet.add v.add(item) v[*] = item
List.get item = v.get(i) item = v[i]
Iterator.next r = iterator.next() r = iterator[*]

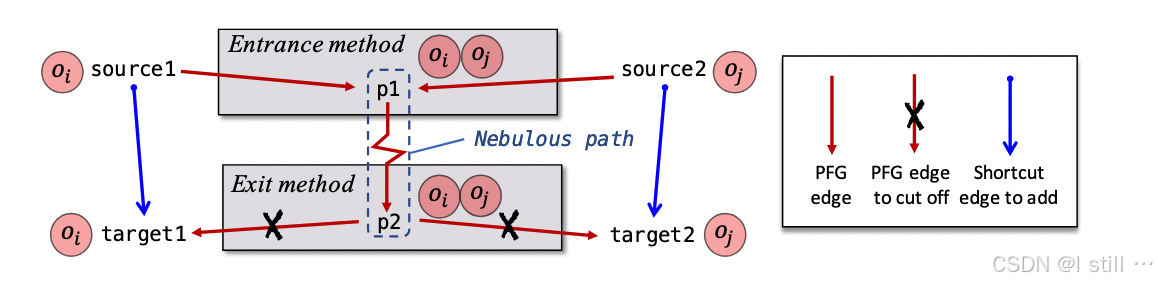
下面例子中containter的指向集有 pts ( l 1 ) = { o l 1 } \text{pts}(l_1) = \{ o_{l_1} \} pts(l1)={ol1}, pts ( l 2 ) = { o l 2 } \text{pts}(l_2) = \{ o_{l_2} \} pts(l2)={ol2}，而有 pts ( o l 1 [ ∗ ] ) = { o a } \text{pts}(o_{l_1}[*]) = \{ o_a \} pts(ol1[∗])={oa}, pts ( o l 2 ) = { o b } \text{pts}(o_{l_2}) = \{ o_b \} pts(ol2)={ob}（这里将 List 近似为 Array ）。按照标准指针分析规则不考虑对container建模的话则 pts ( o l 1 [ ∗ ] ) = pts ( o l 2 [ ∗ ] ) = { o a , o b } \text{pts}(o_{l_1}[*]) = \text{pts}(o_{l_2}[*]) = \{ o_a, o_b \} pts(ol1[∗])=pts(ol2[∗])={oa,ob}，也就是不同container object调用的 get 方法会返回同样的object。这里Cut-Shortcut的目标是在container的 add 等方法的参数和 get、Iterator.next() 方法的返回值间构造PFG边，让不同container object（ o l 1 o_{l_1} ol1, o l 2 o_{l_2} ol2）的Exit方法（get）返回不同的object。

java 复制代码 
ArrayList l1 = new ArrayList(); // pts(l1) = { ol1 }
Object a = new Object(); // oa
l1.add(a); // ENTRANCE, a is SOURCE
Object x = l1.get(0); //EXIT, x is TARGET

ArrayList l2 = new ArrayList(); // pts(l2) = { ol2 }
Object b = new Object(); // ob
l2.add(b); // ENTRANCE, b is SOURCE
Object y = l2.get(0); //EXIT, y is TARGET

Iterator it1 = l1.iterator(); // ptsH(it1) = { ol1 }
Object r1 = it1.next(); // EXIT, r1 is TARGET
Iterator it2 = l2.iterator(); // ptsH(it2) = { ol2 }
Object r2 = it2.next(); // EXIT, r2 is TARGET

在Cut-Shortcut 中，作者将container中的元素划分为三类：集合类（Set、List）的值，记为 c cv c_{\text{cv}} ccv）、Map 的keys（记为 c mk c_{\text{mk}} cmk）、 Map 的values（记为 c mv c_{\text{mv}} cmv）。Cut-Shortcut对容器采用array-insensitive与flow-insensitive的抽象建模：List.get 和 Map.get 的返回值可能为容器中任意曾存入的元素；同时未处理 pop 等删除操作涉及的strong-update，仅进行纯增量分析。同时给容器变量设置额外host指向 pts H \text{pts}_H ptsH 表示。例如， pts H ( l 1 ) = { o l 1 } \text{pts}H(l_1) = \{ o{l_1} \} ptsH(l1)={ol1}， pts H ( l 2 ) = { o l 2 } \text{pts}H(l_2) = \{ o{l_2} \} ptsH(l2)={ol2}。

relation 说明
Entrance 用三元组 ⟨ m , k , c ⟩ \langle m, k, c \rangle ⟨m,k,c⟩ 表示， m m m 是container entrance method (add, put 之类)，传递给第 k k k 个参数的value属于第 c c c 个类别的element。entrance方法的建模通常不考虑返回值，假设它是 void 类型
Exit 用二元组 ⟨ m , c ⟩ \langle m, c \rangle ⟨m,c⟩ 表示， m m m 是container exit method (get 之类)，返回值属于第 c c c 个类别的element。这里不考虑 get 的索引，进行array-insensitive的分析。此外 Iterator.next() 方法可以获取container元素，也是一种Exit方法。Exit 方法通常不考虑参数，假设返回值可以接收container中所有对象。
Transfer 处理 iterator 这种情况，在Cut-Shortcut的建模中 Container.iterator() 的指向集和 Container 相同。因此 iterator() 属于一种Transfer方法。

在Cut-Shortcut的规则中，container的 pts \text{pts} pts 复制到 pts H \text{pts}_H ptsH 中，随后基于下面规则传播 pts H \text{pts}_H ptsH 中并基于此构建PFG edge并删除部分PFG edge，新构建的PFG传播 pts \text{pts} pts 最终精简container变量的 pts \text{pts} pts 集。

规则名称 处理规则 功能描述
[CutContainer] m ret ∈ cutReturns ∣ ⟨ m , c k ⟩ ∈ Exit m_{\text{ret}} \in \text{cutReturns} \mid \langle m, c_k \rangle \in \text{Exit} mret∈cutReturns∣⟨m,ck⟩∈Exit 切断Exit方法 (List.get, Map.get, Iterator.next()) 的返回值到callsite左值的返回边
[HostSource] o ⇚ c l a k ∣ l : v . k ( l a 1 , . . . ) , l → m ∈ CG , ⟨ m , k , c ⟩ ∈ Entrance , o ∈ pts H ( v ) o \stackrel{c}\Lleftarrow l_{a_k} \mid l: v.k(l_{a_1}, ...), l \rightarrow m \in \text{CG}, \langle m, k, c \rangle \in \text{Entrance}, o \in \text{pts}_H(v) o⇚clak∣l:v.k(la1,...),l→m∈CG,⟨m,k,c⟩∈Entrance,o∈ptsH(v) 上面示例中，存在entrance ⟨ ArrayList . add , 0 , c 1 ⟩ \langle \text{ArrayList}.\text{add}, 0, c_1 \rangle ⟨ArrayList.add,0,c1⟩, pts H ( l 1 ) = { o l 1 } \text{pts}H(l_1) = \{ o{l_1} \} ptsH(l1)={ol1}，因此可以推导出 o l 1 ⇚ c 1 a o_{l_1} \stackrel{c_1}\Lleftarrow a ol1⇚c1a 表示 a a a 的值被写入container对象 o l 1 o_{l_1} ol1。
[HostTarget] o ⇛ c x ∣ l : x = v . k ( l a 1 , . . . ) , l → m ∈ CG , ⟨ m , c ⟩ ∈ Exit , o ∈ pts H ( v ) o \stackrel{c}\Rrightarrow x \mid l: x = v.k(l_{a_1}, ...), l \rightarrow m \in \text{CG}, \langle m, c \rangle \in \text{Exit}, o \in \text{pts}_H(v) o⇛cx∣l:x=v.k(la1,...),l→m∈CG,⟨m,c⟩∈Exit,o∈ptsH(v) 上面示例中，exit ⟨ ArrayList . exit , c 1 ⟩ \langle \text{ArrayList}.\text{exit}, c_1 \rangle ⟨ArrayList.exit,c1⟩, pts H ( l 1 ) = { o l 1 } \text{pts}H(l_1) = \{ o{l_1} \} ptsH(l1)={ol1}，因此可以推导出 o l 1 ⇛ c 1 x o_{l_1} \stackrel{c_1}\Rrightarrow x ol1⇛c1x。
[ShortcutContainer] s → t ∈ PFG ∣ o ⇚ c s , o ⇛ c t s \rightarrow t \in \text{PFG} \mid o \stackrel{c}\Lleftarrow s, o \stackrel{c}\Rrightarrow t s→t∈PFG∣o⇚cs,o⇛ct o ⇚ c s o \stackrel{c}\Lleftarrow s o⇚cs 和 o ⇛ c t o \stackrel{c}\Rrightarrow t o⇛ct 表示如果 s s s 的值被写入container对象 o o o，而 t t t 则从 o o o 中读取值，且类型相等，那么 s s s, t t t 之间存在value-flow。比如示例中，前面构建了 o l 1 ⇚ c 1 b o_{l_1} \stackrel{c_1}\Lleftarrow b ol1⇚c1b 和 o l 1 ⇛ c 1 x o_{l_1} \stackrel{c_1}\Rrightarrow x ol1⇛c1x，那么有 a → x a \rightarrow x a→x。
[ColHost] 和 [MapHost] o ∈ pts H ( x ) ∣ o ∈ pts ( x ) , Type ( o ) ∈ { Collecton , Map } o \in \text{pts}_H(x) \mid o \in \text{pts}(x), \text{Type}(o) \in \{ \text{Collecton}, \text{Map} \} o∈ptsH(x)∣o∈pts(x),Type(o)∈{Collecton,Map} 对于指针 x x x，其指向集中 Collection, Map 类型的object会被加入到 pts H \text{pts}_H ptsH 中，这里可能考虑到某些基础类型（Object）指针可能指向 String 或者Container类型的object，因此需要排除 String object。
[TransferHost] pts H ( v ) ⊆ pts H ( x ) ∣ l : x = v . k ( ) , l → m ∈ CG , m ∈ Transfers \text{pts}_H(v) \subseteq \text{pts}_H(x) \mid l: x = v.k(), l \rightarrow m \in \text{CG}, m \in \text{Transfers} ptsH(v)⊆ptsH(x)∣l:x=v.k(),l→m∈CG,m∈Transfers 对于 iterator() 等Transfer方法的调用，将base变量的 pts H \text{pts}_H ptsH 传递给receiver。示例中 pts H ( l 1 ) = { o l 1 } \text{pts}H(l_1) = \{ o{l_1} \} ptsH(l1)={ol1}，那么则推导出 pts H ( it 1 ) = { o l 1 } \text{pts}_H(\text{it}1) = \{ o{l_1} \} ptsH(it1)={ol1}
[PortHost] pts H ( m ret ) ⊆ pts H ( t ) ∣ m ret → t ∈ PFG , ¬ ( l : t = v . k ( . . . ) ∧ l → m ∈ CG ∧ m ∈ Transfers ) \text{pts}H(m{\text{ret}}) \subseteq \text{pts}H(t) \mid m{\text{ret}} \rightarrow t \in \text{PFG}, \neg (l: t = v.k(...) \wedge l \rightarrow m \in \text{CG} \wedge m \in \text{Transfers}) ptsH(mret)⊆ptsH(t)∣mret→t∈PFG,¬(l:t=v.k(...)∧l→m∈CG∧m∈Transfers) 沿PFG边传播 pts H \text{pts}_H ptsH，但避免Transfer方法的返回值到其callsite的receiver引入混淆。

这里与ANTaint（参考blog 企业级程序分析框架）对比可发现，ANTaint对 Map 的建模中考虑 put(key, value) 时如果 key 是常量，则将 value 绑定到对应 key 上，不过企业环境下代码更规范，这么做可能回报更多。Cut-Shortcut则不考虑这一点。

Soundness，这里可能影响soundness的地方主要在：

    1. [CutContainer] - 如果调用的是Exit方法比如 v = List.get()、v = Iterator.next()，那么切断callee return到 v 的PFG；通常如果未建模的container API进行保守处理可以规避错误切断return flow。
    1. [HostSource] - 这里我觉得是最有可能出现问题的，假如 v.entrance(a), vi = v.get()；entrance 是未被建模的Entrance API，而 get 是被建模的Exit API。此时 get return到 item 的PFG被切断，此时 pts H ( v ) = { o } \text{pts}_H(v) = \{ o \} ptsH(v)={o}，那么正常有 o ⇚ c v o \stackrel{c}\Lleftarrow v o⇚cv 以及 o ⇛ c v i o \stackrel{c}\Rrightarrow v_i o⇛cvi 从而构造PFG edge v → v i v \rightarrow v_i v→vi，但如果 entrance 没被建模那么 o ⇚ c v o \stackrel{c}\Lleftarrow v o⇚cv 便不存在因此漏过value-flow。与之相比如果Exit方法没被建模那么也就是少了一个cutReturn，其pts依旧可以通过保守指针分析得到，只是精度差些。
    1. [Transfer] - 如果一个Iterator变量 it = v.iterator() 方法没被建模，但是随后有 vi = it.next()，xx.next 被建模为Iter-Exit，那么 xx.next 的return到 vi 的PFG被切断。此时 pts H ( it ) \text{pts}_H(\text{it}) ptsH(it) 出现遗漏导致 pts ( v i ) \text{pts}(v_i) pts(vi) unsound。

2.实现

论文中给出的规则是context-insensitive的，同时原版实现也是如此，context变量全部用 emptyContext。这里我调整了下支持context-sensitive模式。

2.1.CutShortcutSolver

相比DefaultSolver，CutShortcutSolver定义了下面成员变量

成员变量 类型 作用
cutStoreFields Set<StoreField> 保存 cutStores \text{cutStores} cutStores 语句
cutReturnVars Set<Var> 保存 cutReturns \text{cutReturns} cutReturns 变量

在处理逻辑上，CutShortcutSolver相比DefaultSolver：

  • 在 processInstanceStore 中只有不在 cutStoreFields 的 FieldStore 会被处理。

  • 在 processCallEdge 中处理call edge ⟨ c , l ⟩ → ⟨ c t , m ⟩ \langle c, l \rangle \rightarrow \langle c^t, m \rangle ⟨c,l⟩→⟨ct,m⟩（ l : r = . . . l: r = ... l:r=...） 时只有 (1). m ret m_\text{ret} mret 不在 cutReturnVars (2). l l l 不在 recoveredCallSites 时才有 ⟨ c t , m ret ⟩ → ⟨ c , r ⟩ ∈ PFG \langle c^t, m_{\text{ret}} \rangle \rightarrow \langle c, r \rangle \in \text{PFG} ⟨ct,mret⟩→⟨c,r⟩∈PFG，其它参数到callee形参的PFG边都正常构造。

2.2.FieldAccessHandler

在field access处理这块，Cut-Shortcut定义了下面几个类型:

类型 含义
AbstractLoadField tempLoads \text{tempLoads} tempLoads 中的语句。
AbstractStoreField tempStores \text{tempStores} tempStores 中最终被处理转化为PFG边的部分。
GetStatement 相当于 tempLoad \text{tempLoad} tempLoad，表示为 ⟨ m , i , k , f ⟩ \langle m, i, k, f \rangle ⟨m,i,k,f⟩，表明方法 m m m 中存在第 i i i 个返回值被赋值的 FieldLoad 语句 m r e t s [ i ] = m p k . f m_{rets}[i] = m_{p_k}.f mrets[i]=mpk.f 并且 def ( m p k ) = ∅ \text{def}(m_{p_k}) = \emptyset def(mpk)=∅，因此 m m m 的callsite l : r = v . k ( l a 1 , . . . ) l: r = v.k(l_{a_1}, ...) l:r=v.k(la1,...) 的行为包括 FieldLoad 语句 r = l a k . f r = l_{a_k}.f r=lak.f 或者 r = v . f r = v.f r=v.f。这里 m p k m_{p_k} mpk 可为 m this m_{\text{this}} mthis。
SetStatement 相当于 tempStore \text{tempStore} tempStore，表示为 ⟨ m , f , i , j ⟩ \langle m, f, i, j \rangle ⟨m,f,i,j⟩，表明方法 m m m 中存在 FieldStore m p i . f = m p j m_{p_i}.f = m_{p_j} mpi.f=mpj，并且 def ( m p i ) = ∅    ∧ def ( m p j ) = ∅ \text{def}(m_{p_i}) = \emptyset \; \wedge \text{def}(m_{p_j}) = \emptyset def(mpi)=∅∧def(mpj)=∅。这样 m m m 的callsite l : r = v . k ( l a 1 , . . . ) l: r = v.k(l_{a_1}, ...) l:r=v.k(la1,...) 的行为包括 FieldStore 语句 l a i . f / v . f = l a j / v l_{a_i}.f/v.f = l_{a_j}/v lai.f/v.f=laj/v。这里 m p i m_{p_i} mpi 或者 m p j m_{p_j} mpj 可为 m this m_{\text{this}} mthis

同时FieldAccessHandler定义了下面成员变量辅助分析

成员变量 类型 含义
setStatements MultiMap<JMethod, SetStatement> 将 m m m 映射到 tempStores \text{tempStores} tempStores 集合
getStatements MultiMap<JMethod, GetStatement> 将 m m m 映射到 tempLoads \text{tempLoads} tempLoads 集合
abstractLoadFields Map<Var, List<AbstractLoadField>> tempLoads \text{tempLoads} tempLoads 中的top-level最终转化为PFG的 FieldLoad
abstractStoreFields Map<Var, List<AbstractStoreField>> tempStores \text{tempStores} tempStores 中的top-level最终转化为PFG的 FieldStore

Field Access需要的一个关键操作是判断变量之间的数据流关系 x ↦ y x \mapsto y x↦y。在Cut-Shortcut中

2.3.LocalFlowHandler

处理Local Flow，具体代码参考LocalFlowHandler。分析local flow的关键是识别 ⟨ m , k ⟩ ↣ x \langle m, k \rangle \rightarrowtail x ⟨m,k⟩↣x 关系，除了这个关系， o ↣ x o \rightarrowtail x o↣x（ o o o 表示 new 语句 x = & o x = \&o x=&o）也属于允许的赋值关系，同时还考虑callee m m m 是反射调用的情况。首先ParameterIndexOrNewObj类表示一个 ⟨ m , k ⟩ \langle m, k \rangle ⟨m,k⟩ 或者局部 New 语句 x = & o x = \&o x=&o。

java 复制代码 
public record ParameterIndexOrNewObj(boolean isObj, ParameterIndex index, Obj obj) {
    public static ParameterIndexOrNewObj INDEX_THIS = new ParameterIndexOrNewObj(false, THISINDEX, null);

    @Override
    public String toString() {
        return isObj ? obj.toString() : index.toString();
    }
}
成员 类型 作用
directlyReturnParams MultiMap<JMethod, ParameterIndexOrNewObj> directlyReturnParams [ m ] = { ⟨ m , k ⟩ , . . . , o } \text{directlyReturnParams}[m] = \{ \langle m, k \rangle, ..., o \} directlyReturnParams[m]={⟨m,k⟩,...,o} 不为空表示该方法返回值直接来自 m p k m_{p_k} mpk 或者 m m m 中的 New 语句。
方法getVariablesAssignedFromParameters 返回值为 MultiMap<Var, ParameterIndexOrNewObj> 其中 result [ x ] = { ⟨ m , k ⟩ , . . . , o } \text{result}[x] = \{ \langle m, k \rangle, ..., o \} result[x]={⟨m,k⟩,...,o} 表示flow到 x x x 的参数或者object集合，这里 x x x 的任一data-flow path只允许为 Copy、Cast、New 语句，出现其它（Load、Call）那么 result [ x ] = ∅ \text{result}[x] = \emptyset result[x]=∅。局部变量 definitions [ x ] = { l 1 : x = exp 1 , . . . } \text{definitions}[x] = \{ l_1: x = \text{exp}_1, ... \} definitions[x]={l1:x=exp1,...}

对于 l : r = v . k ( l a 1 , . . . ) l: r = v.k(l_{a_1}, ...) l:r=v.k(la1,...)（context c c c 下），如果根据object ⟨ c ′ , o v ⟩ ∈ pts ( ⟨ c , v ⟩ ) \langle c^{'}, o_v \rangle \in \text{pts}(\langle c, v \rangle) ⟨c′,ov⟩∈pts(⟨c,v⟩) 求解出call edge ⟨ c , l ⟩ → ⟨ c t , m ⟩ ∈ CG \langle c, l \rangle \rightarrow \langle c^t, m \rangle \in \text{CG} ⟨c,l⟩→⟨ct,m⟩∈CG 并且 directlyReturnParams [ m ] = { ⟨ m , k ⟩ , ⟨ m , this ⟩ , o } \text{directlyReturnParams}[m] = \{ \langle m, k \rangle, \langle m, \text{this} \rangle, o \} directlyReturnParams[m]={⟨m,k⟩,⟨m,this⟩,o}，如果 m m m 不是反射方法，那么:

    1. ⟨ ⟨ c , r ⟩ , { ⟨ c t , o ⟩ } ⟩ ∈ WL \langle \langle c, r \rangle, \{ \langle c^t, o \rangle \} \rangle \in \text{WL} ⟨⟨c,r⟩,{⟨ct,o⟩}⟩∈WL，表示 c t c^t ct 下新分配的object o o o 会进入 pts ( ⟨ c , r ⟩ ) \text{pts}(\langle c, r \rangle) pts(⟨c,r⟩)。
    1. ⟨ c , l a k ⟩ → ⟨ c , r ⟩ ∈ PFG \langle c, l_{a_k} \rangle \rightarrow \langle c, r \rangle \in \text{PFG} ⟨c,lak⟩→⟨c,r⟩∈PFG。表示 pts ( ⟨ c , l a k ⟩ ) ⊆ pts ( ⟨ c , r ⟩ ) \text{pts}(\langle c, l_{a_k} \rangle) \subseteq \text{pts}(\langle c, r \rangle) pts(⟨c,lak⟩)⊆pts(⟨c,r⟩)。
    1. ⟨ ⟨ c , r ⟩ , ⟨ c ′ , o v ⟩ ⟩ ∈ WL \langle \langle c, r \rangle, \langle c^{'}, o_v \rangle \rangle \in \text{WL} ⟨⟨c,r⟩,⟨c′,ov⟩⟩∈WL，对于 m . this → r m.\text{this} \rightarrow r m.this→r 的value-flow 这里和Tai-e一样，考虑到并不只是 l l l 调用 m m m，因此 pts ( ⟨ c t , m this ⟩ ) \text{pts}(\langle c^t, m_{\text{this}} \rangle) pts(⟨ct,mthis⟩) 可能不止包含 ⟨ c ′ , o v ⟩ \langle c^{'}, o_v \rangle ⟨c′,ov⟩，因此添加PFG edge ⟨ c t , m this ⟩ → ⟨ c , r ⟩ \langle c^t, m_{\text{this}} \rangle \rightarrow \langle c, r \rangle ⟨ct,mthis⟩→⟨c,r⟩ 可能会往 pts ( ⟨ c , r ⟩ ) \text{pts}(\langle c, r \rangle) pts(⟨c,r⟩) 下添加无关object。

反射的处理有些复杂，后面再来讨论。

2.4.ContainerAccessHandler

Container-Access处理起来比前两类复杂的多，主要是因为API种类复杂，除了提到的 List.get 等方法，Map.of、Arrays.asList 可等价于 new + Entrance，一个个针对性的建模工作量大，代码可维护性差，这里只针对常用的API进行建模，其它保守处理。

2.4.1.基础

具体代码参考ContainerAccessHandler。传统的方法会深入容器API内部分析，比如标准分析规则会分析 ArrayList.elementData 的指向集，作者对容器类的Entry、Exit、Transfer类方法建模，提高容器API callsite的指针分析精度，同时容器内部的指针分析结果（比如 pts ( this . elementData ) \text{pts}(\text{this}.\text{elementData}) pts(this.elementData)）不变，如果调用容器的没被建模的方法也不会破坏soundness。

java 复制代码 
public class ArrayList<E> extends AbstractList<E>
        implements List<E>, RandomAccess, Cloneable, java.io.Serializable
{
    private static final Object[] EMPTY_ELEMENTDATA = {};
    
    transient Object[] elementData; // non-private to simplify nested class access

    public ArrayList(int initialCapacity) {
        if (initialCapacity > 0) 
            this.elementData = new Object[initialCapacity];
        else if (initialCapacity == 0) 
            this.elementData = EMPTY_ELEMENTDATA;
        else 
            throw new IllegalArgumentException("Illegal Capacity: "+
                                               initialCapacity); 
    }
    ...
}
类型 方法类型 示例
Entrance append List.add、Set.add、Map.put
Entrance extend List.addAll、Set.addAll、Map.putAll
Entrance array initializer ArrayList.<init>
Exit container - element List.get、Map.get
Exit iterator - element Iterator.next(), Iterator.previous()
Exit MapEntry - key/value MapEntry.getKey(), MapEntry.getValue()
Transfer container - iterator List.iterator()

在实现方面主要是同worklist算法同步，这里作者定义了下面container变量类型， pts H ( ⟨ c , v ⟩ , h ) \text{pts}_H(\langle c, v \rangle, h) ptsH(⟨c,v⟩,h) 表示查询变量 ⟨ c , v ⟩ \langle c, v \rangle ⟨c,v⟩ 对应 h h h 类型的host-object集合。container变量类型如下，通常 MAP_ENTRY_SET, MAP_KEY_SET, MAP_VALUES 可以算 COL_0 的子集，而 MAP_ENTRY_ITR, MAP_KEY_ITR, MAP_VALUE_ITR 算 COL_ITR 的子集。不过作者为了更好分析 Map 就区分开来。

container变量类型 示例
MAP Map, HashMap
MAP_ENTRY_SET Map.entrySet() 的返回值，类型 Set<Map.Entry<K,V>>
MAP_ENTRY_ITR Map.entrySet().iterator() 的返回值
MAP_ENTRY Map.Entry<K, V> 类型的变量
MAP_KEY_SET Map.keySet() 返回值，类型为 Set<K>
MAP_KEY_ITR Map.keySet().iterator() 的返回值
MAP_VALUES Map.values() 的返回值，类型为 Collection<V>
MAP_VALUE_ITR Map.values().iterator() 的返回值
COL Collection, List, Set
COL_ITR Collection.iterator() 的返回值

2.4.2.标准规则实现

1.WorkList Entry

为了方便更新 pts H \text{pts}_H ptsH，作者这里新定义了一种worklist entry HostEntry 表示为 ⟨ ⟨ c , v ⟩ , h , CO ⟩ \langle \langle c, v \rangle, h, \text{CO} \rangle ⟨⟨c,v⟩,h,CO⟩，在 CutShortcut::analyze 中，类似处理 PointerEntry，会进行如下处理：1. DO = CO − pts H ( ⟨ c , v ⟩ , h ) \text{DO} = \text{CO} - \text{pts}_H(\langle c, v \rangle, h) DO=CO−ptsH(⟨c,v⟩,h)，2. CO ⊆ pts H ( ⟨ c , v ⟩ , h ) \text{CO} \subseteq \text{pts}_H(\langle c, v \rangle, h) CO⊆ptsH(⟨c,v⟩,h)，3. ⟨ ⟨ c ′ , v d ⟩ , h , DO ⟩ ∈ WL ∣ ∀ e = ⟨ c , v ⟩ → ⟨ c ′ , v d ⟩ ∈ PFG ∧ canProp ( e ) \langle \langle c^{'}, v_d \rangle, h, \text{DO} \rangle \in \text{WL} \mid \forall e = \langle c, v \rangle \rightarrow \langle c^{'}, v_d \rangle \in \text{PFG} \wedge \text{canProp}(e) ⟨⟨c′,vd⟩,h,DO⟩∈WL∣∀e=⟨c,v⟩→⟨c′,vd⟩∈PFG∧canProp(e)，其中只要 e e e 不是container内部调用视图的返回边，那么 canProp \text{canProp} canProp 为 true，4. 调用ContainerAccessHandler.onNewHostEntry 进一步处理entry ⟨ ⟨ c , v ⟩ , h , DO ⟩ \langle \langle c, v \rangle, h, \text{DO} \rangle ⟨⟨c,v⟩,h,DO⟩。

2.HostSource/HostTarget

在实现层面，对于 ⟨ c ′ , o ⟩ ⇚ cate ⟨ c , v ⟩ \langle c^{'}, o \rangle \stackrel{\text{cate}}\Lleftarrow \langle c, v \rangle ⟨c′,o⟩⇚cate⟨c,v⟩， ⟨ c ′ , o ⟩ ⇛ cate ⟨ c ′ ′ , r ⟩ \langle c^{'}, o \rangle \stackrel{\text{cate}}\Rrightarrow \langle c^{''}, r \rangle ⟨c′,o⟩⇛cate⟨c′′,r⟩；在context-sensitive 下，分别用PFG edge ⟨ c , v ⟩ → ⟨ c ′ , h cate ( o ) ⟩ \langle c, v \rangle \rightarrow \langle c^{'}, h_{\text{cate}}(o) \rangle ⟨c,v⟩→⟨c′,hcate(o)⟩ 和 ⟨ c ′ , h cate ( o ) ⟩ → ⟨ c ′ ′ , r ⟩ \langle c^{'}, h_{\text{cate}}(o) \rangle \rightarrow \langle c^{''}, r \rangle ⟨c′,hcate(o)⟩→⟨c′′,r⟩。

这里 h cate ( o ) h_{\text{cate}}(o) hcate(o) 表示memory object对应 cate \text{cate} cate 的host指针，比如 v = new HashMap(); // allocate o, h mv ( o ) h_\text{mv}(o) hmv(o) 对应 o o o 的Map-Value host， h mk ( o ) h_\text{mk}(o) hmk(o) 对应 o o o 的Map-Key host，而 Collection 的object只有1个Col-Value host。

3.Transfer

paper中定义的 [TransferHost] 为 pts H ( v ) ⊆ pts H ( r ) ∣ l : r = v . k ( ) , l → m ∈ CG , m ∈ Transfers \text{pts}_H(v) \subseteq \text{pts}_H(r) \mid l: r = v.k(), l \rightarrow m \in \text{CG}, m \in \text{Transfers} ptsH(v)⊆ptsH(r)∣l:r=v.k(),l→m∈CG,m∈Transfers，该规则可以处理 Collection.iterator() 调用，但是callee为 Map 的方法则不好用，因此作者补充了 [TransferHost] 规则，完整的规则如下。这里注意虽然 Collection.iterator().next() 属于Exit方法，但是 Map.Entry 是 MapValue 和 MapKey 的wrapper，依旧属于host，所以算作Transfer方法。

下面Transfer关系可以记为 Transfer = { m i : { h m i j s → h m i j d , . . . } \text{Transfer} = \{ m_i: \{ h_{m_{ij}^s} \rightarrow h_{m_{ij}^d}, ... \} Transfer={mi:{hmijs→hmijd,...}，WorkList算法对 [TransferHost] 的处理为 ⟨ ⟨ c , r ⟩ , h m j d , DO ⟩ ∣ ∀ h m j s → h m j d ∈ Transfer ( m ) , ⟨ ⟨ c , v ⟩ , h m j s , DO ⟩ = HostEntry \langle \langle c, r \rangle, h_{m^d_j}, \text{DO} \rangle \mid \forall h_{m^s_j} \rightarrow h_{m^d_j} \in \text{Transfer}(m), \langle \langle c, v \rangle, h_{m^s_j}, \text{DO} \rangle = \text{HostEntry} ⟨⟨c,r⟩,hmjd,DO⟩∣∀hmjs→hmjd∈Transfer(m),⟨⟨c,v⟩,hmjs,DO⟩=HostEntry。

API类型 source变量类型 target变量类型
Collection.iterator() Col Col_ITR
Map.entrySet() MAP MAP_ENTRY_SET
Map.keySet() MAP MAP_KEY_SET
Map.values() MAP MAP_VALUES
Map.entrySet().iterator() MAP_ENTRY_SET MAP_ENTRY_ITR
Map.values().iterator() MAP_VALUES MAP_VALUE_ITR
Map.keySet().iterator() MAP_KEY_SET MAP_KEY_ITR
Map.entrySet().iterator().next() MAP_ENTRY_ITR MAP_ENTRY
class Map.Entry MAP MAP_ENTRY
class Map.keys MAP MAP_KEY_ITR

以 k = m.keySet() 为例，其满足 pts H ( ⟨ c , m ⟩ , map ) ⊆ pts H ( ⟨ c , k ⟩ , map_key_set ) \text{pts}_H(\langle c, m \rangle, \text{map}) \subseteq \text{pts}_H(\langle c, k \rangle, \text{map\_key\_set}) ptsH(⟨c,m⟩,map)⊆ptsH(⟨c,k⟩,map_key_set)。在worklist算法中，如果有entry ⟨ ⟨ c , v ⟩ , map , DO ⟩ \langle \langle c, v \rangle, \text{map}, \text{DO} \rangle ⟨⟨c,v⟩,map,DO⟩，遍历所有callsite r = v . k ( . . . ) r = v.k(...) r=v.k(...)

  • 对于 k = v . keySet ( ) k = v.\text{keySet}() k=v.keySet()，有 ⟨ ⟨ c , k ⟩ , map_key_set , DO ⟩ ∈ WL \langle \langle c, k \rangle, \text{map\_key\_set}, \text{DO} \rangle \in \text{WL} ⟨⟨c,k⟩,map_key_set,DO⟩∈WL。

  • 对于 k = v . values ( ) k = v.\text{values}() k=v.values()，有 ⟨ ⟨ c , k ⟩ , map_values , DO ⟩ ∈ WL \langle \langle c, k \rangle, \text{map\_values}, \text{DO} \rangle \in \text{WL} ⟨⟨c,k⟩,map_values,DO⟩∈WL。

  • 对于 k = v . entrySet ( ) k = v.\text{entrySet}() k=v.entrySet()，有 ⟨ ⟨ c , k ⟩ , map_entry , DO ⟩ ∈ WL \langle \langle c, k \rangle, \text{map\_entry}, \text{DO} \rangle \in \text{WL} ⟨⟨c,k⟩,map_entry,DO⟩∈WL。

其它依此类推

4.Iterator-Exit

这里定义了两种类型的Exit方法，Container-Exit和Iterator-Exit，Container-Exit就是 List.get、Map.put 等方法，Iterator-Exit则是 Iterator.next、Map.Entry.getKey、Map.Entry.getValue 等方法。其具体涉及到的API如下:

API类型 source变量类型 target变量类型
Map.Entry.getKey() MAP_ENTRY MapKey
Map.Entry.getValue() MAP_ENTRY MapValue
Map.keySet().iterator().next() MAP_KEY_ITR MapKey
Map.values().iterator().next() MAP_VALUE_ITR MapValue
Collection.iterator().next() COL_ITR ColValue

从container object到 ColValue, MapKey, MapValue 的Transfer-Exit path如下，可以看到 Map 相比 Collection 多了以及path且传播方式更加丰富。
iterator+transfer
next+exit
entrySet+transfer
iterator+transfer
next+transfer
getKey+exit
getValue+exit
keySet+transfer
iterator+transfer
next+exit
values+transfer
iterator+transfer
next+exit
Col
COL_ITR
COL_VALUE
MAP
MAP_ENTRY_SET
MAP_ENTRY_ITR
MAP_ENTRY
MAP_KEY
MAP_VALUE
MAP_KEY_SET
MAP_KEY_ITR
MAP_VALUES
MAP_VALUE_ITR

需要注意的是对于 Map.EntrySet，其Iterator.next为 Transfer，而其它 Collection.Iterator.next 都是 Exit。例子 ：以 v = k.getKey() 为例，处理worklist entry ⟨ ⟨ c , k ⟩ , map_entry_itr , DO ⟩ \langle \langle c, k \rangle, \text{map\_entry\itr}, \text{DO} \rangle ⟨⟨c,k⟩,map_entry_itr,DO⟩ 时，对应规则为 ⟨ c ′ , h m k ( o ) ⟩ → ⟨ c , v ⟩ ∈ PFG ∣ ∀ ⟨ c ′ , o ⟩ ∈ DO \langle c^{'}, h{mk}(o) \rangle \rightarrow \langle c, v \rangle \in \text{PFG} \mid \forall \langle c^{'}, o \rangle \in \text{DO} ⟨c′,hmk(o)⟩→⟨c,v⟩∈PFG∣∀⟨c′,o⟩∈DO 。

5.Extrance-Extend

对应 l1.addAll(l2) 这种，作者建模了下面几种情况

场景 示例 规则
Collection --> Collection vd.addAll(vs) ⟨ c ′ ′ , h c ( o s ) ⟩ → ⟨ c ′ , h c ( o d ) ⟩ ∈ PFG ∣ ∀ ⟨ c ′ , o d ⟩ ∈ pts H ( ⟨ c , v d ⟩ , col ) , ∀ ⟨ c ′ ′ , o s ⟩ ∈ pts H ( ⟨ c , v s ⟩ , col ) \langle c^{''}, h_c(o_s) \rangle \rightarrow \langle c^{'}, h_c(o_d) \rangle \in \text{PFG} \mid \forall \langle c^{'}, o_d \rangle \in \text{pts}_H(\langle c, v_d \rangle, \text{col}), \forall \langle c^{''}, o_s \rangle \in \text{pts}_H(\langle c, v_s \rangle, \text{col}) ⟨c′′,hc(os)⟩→⟨c′,hc(od)⟩∈PFG∣∀⟨c′,od⟩∈ptsH(⟨c,vd⟩,col),∀⟨c′′,os⟩∈ptsH(⟨c,vs⟩,col)
Map.keySet --> Collection vs = m.keySet(), vd.addAll(vs) ⟨ c ′ ′ , h mk ( o s ) ⟩ → ⟨ c ′ , h c ( o d ) ⟩ ∈ PFG ∣ ∀ ⟨ c ′ , o d ⟩ ∈ pts H ( ⟨ c , v d ⟩ , col ) , ∀ ⟨ c ′ ′ , o s ⟩ ∈ pts H ( ⟨ c , v s ⟩ , map_key_set ) \langle c^{''}, h_{\text{mk}}(o_s) \rangle \rightarrow \langle c^{'}, h_c(o_d) \rangle \in \text{PFG} \mid \forall \langle c^{'}, o_d \rangle \in \text{pts}_H(\langle c, v_d \rangle, \text{col}), \forall \langle c^{''}, o_s \rangle \in \text{pts}_H(\langle c, v_s \rangle, \text{map\_key\_set}) ⟨c′′,hmk(os)⟩→⟨c′,hc(od)⟩∈PFG∣∀⟨c′,od⟩∈ptsH(⟨c,vd⟩,col),∀⟨c′′,os⟩∈ptsH(⟨c,vs⟩,map_key_set)
Map.values --> Collection vs = m.values(), vd.addAll(vs) ⟨ c ′ ′ , h mv ( o s ) ⟩ → ⟨ c ′ , h c ( o d ) ⟩ ∈ PFG ∣ ∀ ⟨ c ′ , o d ⟩ ∈ pts H ( ⟨ c , v d ⟩ , col ) , ∀ ⟨ c ′ ′ , o s ⟩ ∈ pts H ( ⟨ c , v s ⟩ , map_values ) \langle c^{''}, h_{\text{mv}}(o_s) \rangle \rightarrow \langle c^{'}, h_c(o_d) \rangle \in \text{PFG} \mid \forall \langle c^{'}, o_d \rangle \in \text{pts}_H(\langle c, v_d \rangle, \text{col}), \forall \langle c^{''}, o_s \rangle \in \text{pts}_H(\langle c, v_s \rangle, \text{map\_values}) ⟨c′′,hmv(os)⟩→⟨c′,hc(od)⟩∈PFG∣∀⟨c′,od⟩∈ptsH(⟨c,vd⟩,col),∀⟨c′′,os⟩∈ptsH(⟨c,vs⟩,map_values)
Map --> Map vd.addAll(vs) ⟨ c ′ ′ , h mv ( o s ) ⟩ → ⟨ c ′ , h mv ( o d ) ⟩ ∈ PFG , ⟨ c ′ ′ , h mk ( o s ) ⟩ → ⟨ c ′ , h mk ( o d ) ⟩ ∈ PFG ∣ ∀ ⟨ c ′ , o d ⟩ ∈ pts H ( ⟨ c , v d ⟩ , map ) , ∀ ⟨ c ′ ′ , o s ⟩ ∈ pts H ( ⟨ c , v s ⟩ , map ) \langle c^{''}, h_{\text{mv}}(o_s) \rangle \rightarrow \langle c^{'}, h_{\text{mv}}(o_d) \rangle \in \text{PFG}, \langle c^{''}, h_{\text{mk}}(o_s) \rangle \rightarrow \langle c^{'}, h_{\text{mk}}(o_d) \rangle \in \text{PFG} \mid \forall \langle c^{'}, o_d \rangle \in \text{pts}_H(\langle c, v_d \rangle, \text{map}), \forall \langle c^{''}, o_s \rangle \in \text{pts}_H(\langle c, v_s \rangle, \text{map}) ⟨c′′,hmv(os)⟩→⟨c′,hmv(od)⟩∈PFG,⟨c′′,hmk(os)⟩→⟨c′,hmk(od)⟩∈PFG∣∀⟨c′,od⟩∈ptsH(⟨c,vd⟩,map),∀⟨c′′,os⟩∈ptsH(⟨c,vs⟩,map)

worklist实现的有点复杂，分别放在 onNewCallEdge 和 onNewHostEntry 中，核心思想就是考虑 pts H ( ⟨ c , v ⟩ ) \text{pts}_H(\langle c, v \rangle) ptsH(⟨c,v⟩) 改变时，需要更新host变量 ⟨ c ′ , h ( o ) ⟩ \langle c^{'}, h(o) \rangle ⟨c′,h(o)⟩ 的PFG。

6.Entrance-Array Initializer

包括构造方法 ArrayList(Object []) 以及 Collections.addAll(List, Object[])，这里简化为callsite l : add ( v d , v s ) l: \text{add}(v_d, v_s) l:add(vd,vs)，规则为： ⟨ c ′ , o d ⟩ ⇚ col ⟨ c ′ ′ , o s [ ∗ ] ⟩ ∣ ∀ ⟨ c ′ ′ , o s ⟩ ∈ pts ( ⟨ c , v s ⟩ ) , ∀ ⟨ c ′ , o d ⟩ ∈ pts H ( ⟨ c , v d ⟩ ) \langle c^{'}, o_d \rangle \stackrel{\text{col}}\Lleftarrow \langle c^{''}, o_s[*] \rangle \mid \forall \langle c^{''}, o_s \rangle \in \text{pts}(\langle c, v_s \rangle), \forall \langle c^{'}, o_d \rangle \in \text{pts}_H(\langle c, v_d \rangle) ⟨c′,od⟩⇚col⟨c′′,os[∗]⟩∣∀⟨c′′,os⟩∈pts(⟨c,vs⟩),∀⟨c′,od⟩∈ptsH(⟨c,vd⟩)，表示 Array v s v_s vs 中存的每个指针变量 o s [ ∗ ] o_s[*] os[∗] 都会添加到container v d v_d vd 变量的每个container object o d o_d od 下。

具体实现层面，考虑到 pts ( ⟨ c , v s ⟩ ) \text{pts}(\langle c, v_s \rangle) pts(⟨c,vs⟩) 和 pts ( ⟨ c , v d ⟩ ) \text{pts}(\langle c, v_d \rangle) pts(⟨c,vd⟩) 都是随worklist算法逐步更新的。为了方便处理，对于 l l l，引入辅助变量 arr l \text{arr}_l arrl:

  • 在第一次处理 ⟨ c , l ⟩ → ⟨ c t , m ⟩ \langle c, l \rangle \rightarrow \langle c^t, m \rangle ⟨c,l⟩→⟨ct,m⟩ 时，有 ⟨ c ′ ′ , o s [ ∗ ] ⟩ → ⟨ c , arr l ⟩ ∈ PFG ∣ ∀ ⟨ c ′ ′ , o s ⟩ ∈ pts ( ⟨ c , v s ⟩ ) \langle c^{''}, o_s[*] \rangle \rightarrow \langle c, \text{arr}_l \rangle \in \text{PFG} \mid \forall \langle c^{''}, o_s \rangle \in \text{pts}(\langle c, v_s \rangle) ⟨c′′,os[∗]⟩→⟨c,arrl⟩∈PFG∣∀⟨c′′,os⟩∈pts(⟨c,vs⟩)， ⟨ c , arr l ⟩ → ⟨ c , h cv ( o d ) ⟩ ∈ PFG ∣ ∀ ⟨ c ′ , o d ⟩ ∈ pts H ( ⟨ c , v d ⟩ , col ) \langle c, \text{arr}l \rangle \rightarrow \langle c, h{\text{cv}}(o_d) \rangle \in \text{PFG} \mid \forall \langle c^{'}, o_d \rangle \in \text{pts}_H(\langle c, v_d \rangle, \text{col}) ⟨c,arrl⟩→⟨c,hcv(od)⟩∈PFG∣∀⟨c′,od⟩∈ptsH(⟨c,vd⟩,col)。

  • 处理worklist pointer entry ⟨ ⟨ c , v s ⟩ , DO s ⟩ \langle \langle c, v_s \rangle, \text{DO}_s \rangle ⟨⟨c,vs⟩,DOs⟩ 时，有 ⟨ c ′ ′ , o s [ ∗ ] ⟩ → ⟨ c , arr l ⟩ ∈ PFG ∣ ∀ ⟨ c ′ ′ , o s ⟩ ∈ DO s \langle c^{''}, o_s[*] \rangle \rightarrow \langle c, \text{arr}_l \rangle \in \text{PFG} \mid \forall \langle c^{''}, o_s \rangle \in \text{DO}_s ⟨c′′,os[∗]⟩→⟨c,arrl⟩∈PFG∣∀⟨c′′,os⟩∈DOs。

  • 处理worklist host entry ⟨ ⟨ c , v d ⟩ , col , DO d ⟩ \langle \langle c, v_d \rangle, \text{col}, \text{DO}_d \rangle ⟨⟨c,vd⟩,col,DOd⟩ 时，有 ⟨ c , arr l ⟩ → ⟨ c , h col ( o d ) ⟩ ∣ ∀ ⟨ c ′ , o d ⟩ ∈ DO d \langle c, \text{arr}l \rangle \rightarrow \langle c, h{\text{col}}(o_d) \rangle \mid \forall \langle c^{'}, o_d \rangle \in \text{DO}_d ⟨c,arrl⟩→⟨c,hcol(od)⟩∣∀⟨c′,od⟩∈DOd。

这部分规则看起来比较完善，但实际运行起来却发现还是存在merge flow的问题，主要问题就是分析 pts H ( v d ) \text{pts}_H(v_d) ptsH(vd) 时，没有屏蔽Array-Initializer内部实现，比如下面代码 Test 调用了 Collections.addAll。理论上 pts H ( l 1 ) \text{pts}_H(l_1) ptsH(l1) 只包含 a 1 a_1 a1 相关的信息，但是analyzer没有屏蔽 Collections.addAll，分析内部 c.add(element) 时把 a 2 a_2 a2 的信息也算上了。而 Array$ArrayList <init> 就更难优化了，它是被 Arrays.asList 调用的，application-code不能直接访问。因此下面示例中， pts H ( l 3 ) \text{pts}_H(l_3) ptsH(l3) 和 pts H ( l 4 ) \text{pts}_H(l_4) ptsH(l4) 会包括 item1 到 item4 的信息。一个解决的办法是屏蔽API内部机制，但这样一来 pts \text{pts} pts 的side-effect也没了，造成unsoundness。

java 复制代码 
public void Test() {
	Collections.addAll(l1, a1);
	Collections.addAll(l2, a2);

  l3 = Arrays.asList(item1, item2);
  l4 = Arrays.asList(item3, item4);
}

@SafeVarargs
public static <T> boolean addAll(Collection<? super T> c, T... elements) {
    boolean result = false;
    for (T element : elements)
       result |= c.add(element);
    return result;
}

2.4.3.额外规则

Container access旨在通过建模容器API简化应用代码分析，但由于实际API数量庞大且难以穷尽归类，需依赖容器内部的传播规则进行补充处理。例如，List.subList 方法虽未被显式建模，但其返回 ArrayList$SubList 对象时会触发容器传播：构造函数 ArrayList$SubList.<init> 通过 Entrance-Extend 机制传播 pts H \text{pts}_H ptsH​，可抽象为 v = new SubList(); addAll(v, this)。因此，分析中需考虑 this 为容器的情形。其传播规则与Tai-e的标准Cal规则类似：对于调用语句 ⟨ c , l : r = v . k ( . . . ) ⟩ → ⟨ c t , m ⟩ \langle c, l: r = v.k(...) \rangle \rightarrow \langle c^t, m \rangle ⟨c,l:r=v.k(...)⟩→⟨ct,m⟩ 一样，有 pts H ( ⟨ c , v ⟩ ) ⊆ pts H ( ⟨ c t , m this ⟩ ) \text{pts}_H(\langle c, v \rangle) \subseteq \text{pts}H(\langle c^t, m{\text{this}} \rangle) ptsH(⟨c,v⟩)⊆ptsH(⟨ct,mthis⟩)。

java 复制代码 
public List<E> subList(int fromIndex, int toIndex) {
    subListRangeCheck(fromIndex, toIndex, size);
    return new SubList(this, 0, fromIndex, toIndex); // o
}

由于无法穷尽列举所有容器的 entrance 与 exit 方法，若对所有 Collection 和 Map 子类的方法进行分析，反而可能遗漏关键的entrance/exit，导致分析结果unsound。因此，实际实现中仅对常用容器API及其类型进行显式建模。具体而言，仅当存在传播路径 o ⇚ c s o \stackrel{c}\Lleftarrow s o⇚cs 和 o ⇛ c t o \stackrel{c}\Rrightarrow t o⇛ct 且 Type ( o ) \text{Type}(o) Type(o) 属于已建模类型时，才构造 s → t s \rightarrow t s→t；否则，在对应 exit 调用（如 t = v.get(...)）处，需将callee的返回值保守地恢复callsite的PFG。该保守策略的触发条件为：若容器变量 v v v 的 pts H \text{pts}_H ptsH 中包含任意类型未建模的container object（即 notModeled ( Type ( o ) ) ∣ ∃ o ∈ pts H ( v ) \text{notModeled}(\text{Type}(o)) \mid \exist o \in \text{pts}_H(v) notModeled(Type(o))∣∃o∈ptsH(v)，则对相关操作进行保守处理。

除此之外由于存在 Entrance-Extend 方法 addAll ( v d , v s ) \text{addAll}(v_d, v_s) addAll(vd,vs)，则有 setTaint ( o d ) , ∀ o d ∈ pts H ( v d ) ∣ ∃ o s ∈ pts H ( v s ) , notModel ( Type ( o s ) ) \text{setTaint}(o_d), \forall o_d \in \text{pts}_H(v_d) \mid \exist o_s \in \text{pts}_H(v_s), \text{notModel}(\text{Type}(o_s)) setTaint(od),∀od∈ptsH(vd)∣∃os∈ptsH(vs),notModel(Type(os))，setTaint 表示 o d o_d od 不再被视为host。相应地，后续对 v d v_d vd 的 exit 调用（如 i = v.exit()）将根据callee返回值到callsite PFG edge进行保守处理。例如下面代码中，当 list 被自定义容器类型变量 customArrayList 更新后，由于其 pts H \text{pts}_H ptsH​ 包含tainted object，item = list.get(0) 将被保守分析。

java 复制代码 
list = new ArrayList();
list.addAll(customArrayList); // type customArrayList
item = list.get(0);

3.可以改进的地方

Cut-Shortcut实现层面最复杂的问题应该是Container Access分析，毕竟涉及到对API建模，不过人工写API的规则感觉哪怕只考虑1个jdk版本工程量、维护难度都不低，如果考虑jdk 8、17、21等那就更复杂了。以后这部分应该需要靠LLM驱动。

目前版本存在的问题 : 原版主要对 java.util.* 下的container API以及 sun、javax 等包下的API进行建模。这里导出 java.util.* 下的，包括下面列出来的，不过用Tai-e提高的java-benchmarks的JRE8分析java-8的IR时发现 java.util.concurrent 下的 PriorityBlockingQueue、ConcurrentSkipListSet、CopyOnWriteArraySet、ConcurrentSkipListMap、ScheduledThreadPoolExecutor$DelayedWorkQueue 相关的API没有被正常加载，简单debug了一下感觉可能是soot的前端出了点问题，这里需要一些调整。

尚未支持的特性 : Cut-Shortcut目前并没有对流式编程相关API进行建模，比如 Spliterator、forEach、stream。按照传统的方法分析流式代码得用context-sensitive方法提高精度，如果靠建模API提升精度的话规则不是很好写。目前哪怕是基础的container API也无法全部穷举，算上 array --> container 的value-flow规则就更复杂了，还要考虑API版本更新带来的变化，因此个人感觉以后的代码分析还得LLM驱动。

相关推荐
I still …1 个月前
静态分析工具Tai-e
程序分析
I still …2 个月前
MCP servers分析
程序分析·漏洞检测
I still …3 个月前
Rust内存问题检测
rust·程序分析·漏洞检测
I still …1 年前
LLM与动态符号执行生成测试用例的比较
测试用例·程序分析
网络研究院2 年前
x64dbg: 用于Windows的开源二进制调试器
网络安全·软件分析·程序分析·动态分析·逆向工程·调试器·反汇编程序
I still …2 年前
LLM 4 Vulnerability Detection
大模型·程序分析·漏洞检测
boss-dog2 年前
Valgrind——程序分析工具
程序分析·内存泄漏·valgrind
青衫客363 年前
Some optimizations based on analyzing program dynamic behavior
软件分析·程序分析
青衫客363 年前
Memory Access Tracing
软件分析·程序分析
热门推荐
01从零搭建一个 PHP 登录注册系统（含完整源码）02GitHub 镜像站点03AI Agent 平台横评：ZeroClaw vs OpenClaw vs Nanobot04使用 1panel面板 部署 php网站05MIUI显示/隐藏5G开关的方法，信号弱时开启手机Wifi通话方法06openClaw安装飞书插件｜核心踩坑：spawn EINVAL 错误终极解决指南07Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services08配置 OpenClaw 使用 Ollama 本地模型09全面体验 Grok API 中转站（2025 · Grok 4 系列最新版）10让你的代码更整洁：10 个必知的 Kotlin 扩展函数