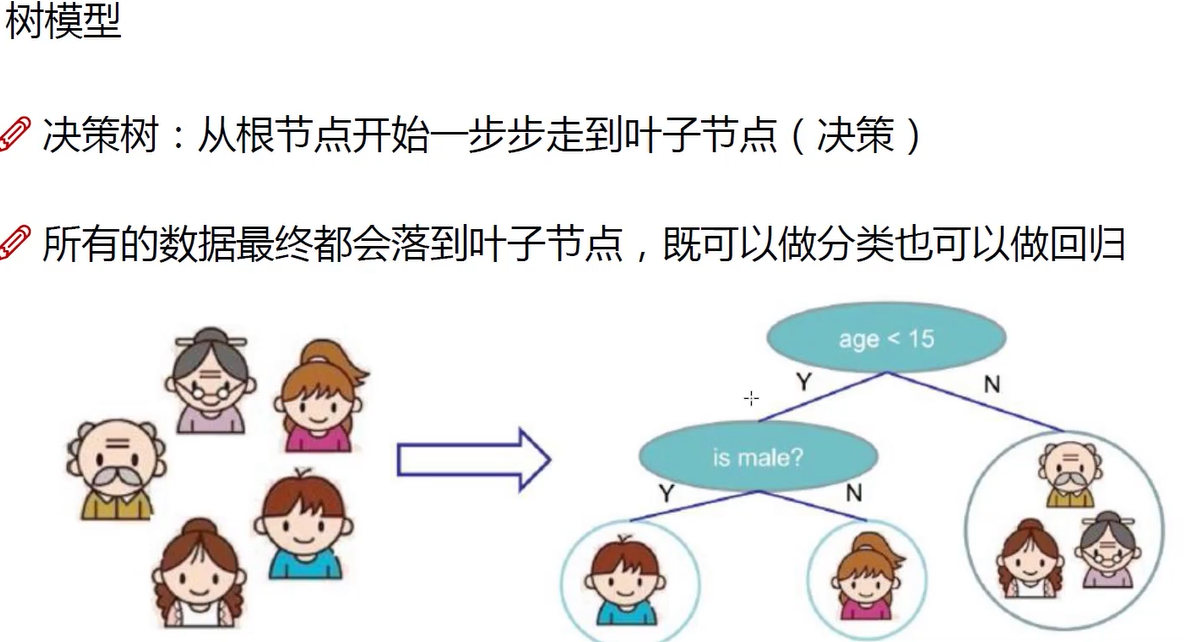
决策树中的条件顺序有严格要求,调换顺序会导致结果差异极大。类似于上场的首发和替补。根节点(首发)必须是分类效果最强、可以筛选大批量的特征,其后的结点(替补)则是细微调控的特征。
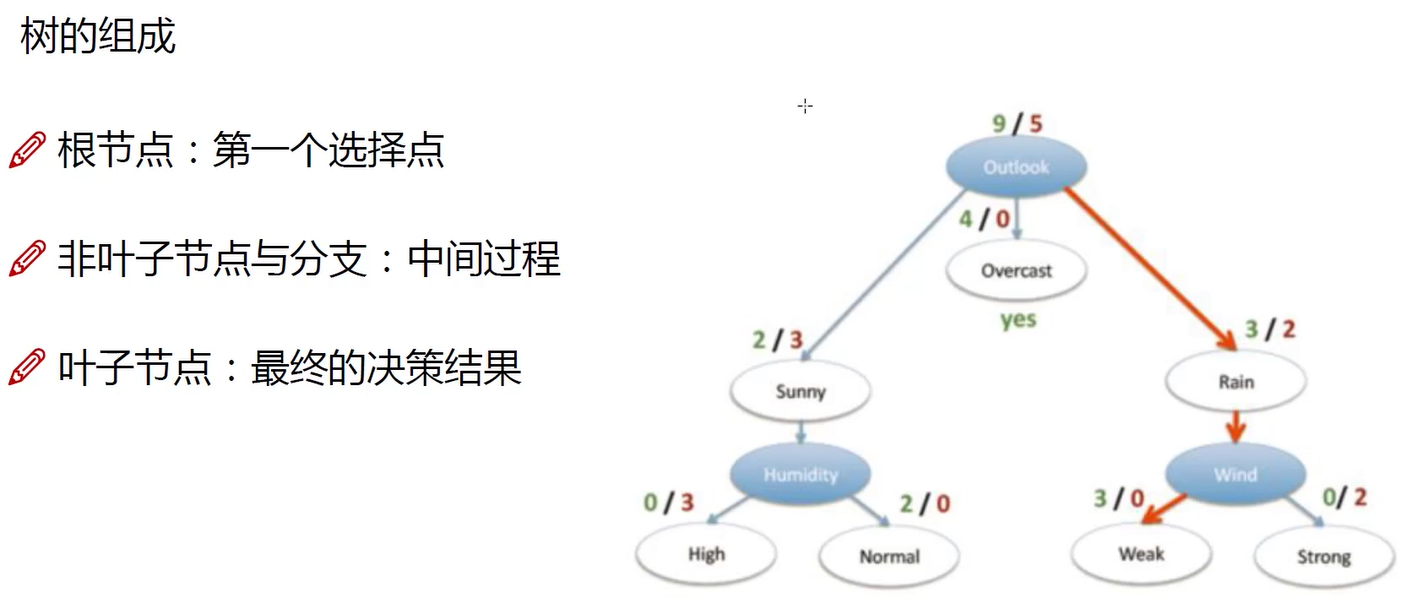



因为概率在0-1之间,所有用对数函数。
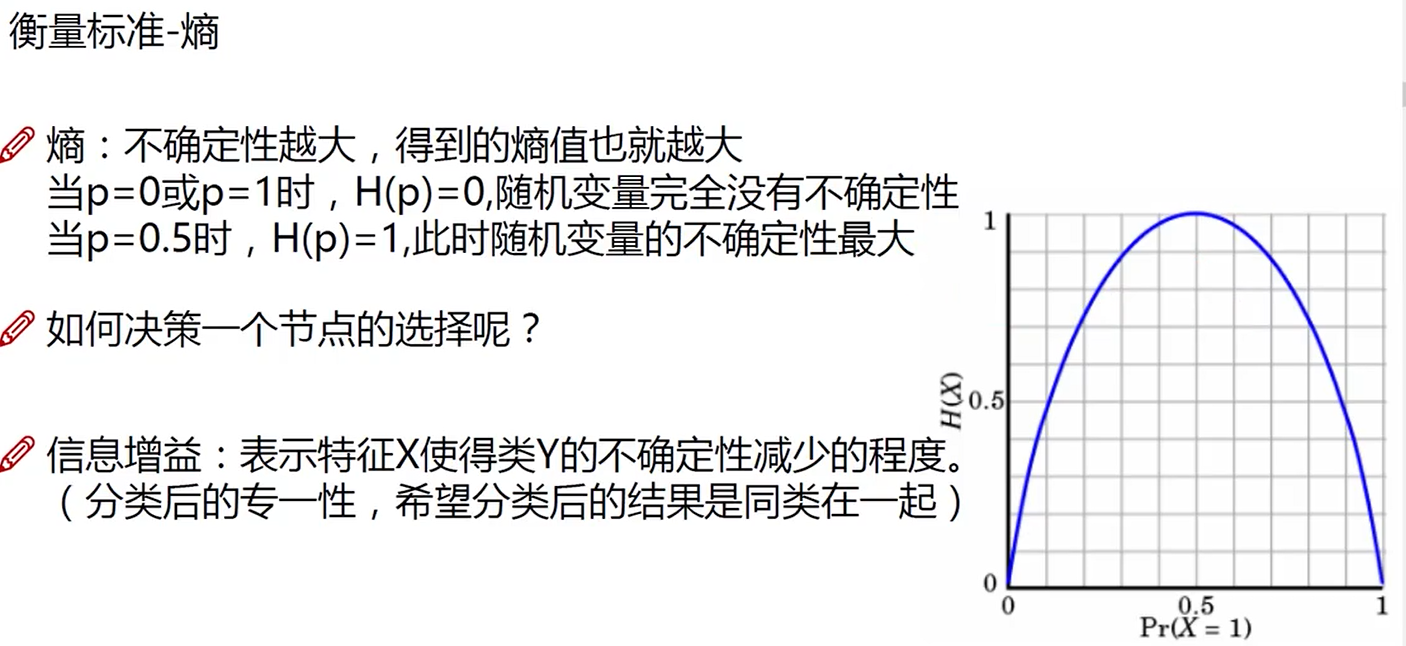
通过分类后,希望熵值下降,即不确定性减少。所以要对比熵值下降的多少来判断特征先后顺序。
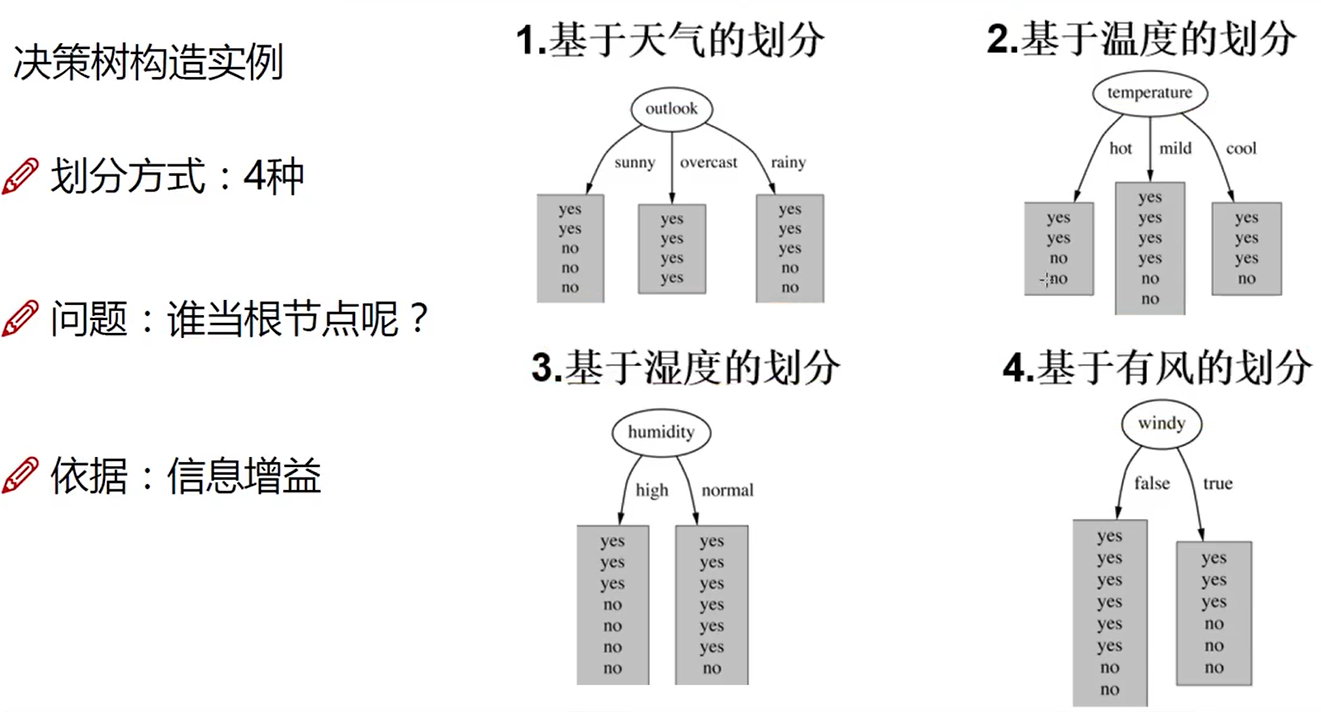

同一特征判决时,不同情况加权重。

信息增益降序排列,取最大的那个特征作根节点,以此类推。

决策树中的条件顺序有严格要求,调换顺序会导致结果差异极大。类似于上场的首发和替补。根节点(首发)必须是分类效果最强、可以筛选大批量的特征,其后的结点(替补)则是细微调控的特征。




因为概率在0-1之间,所有用对数函数。
通过分类后,希望熵值下降,即不确定性减少。所以要对比熵值下降的多少来判断特征先后顺序。



同一特征判决时,不同情况加权重。

信息增益降序排列,取最大的那个特征作根节点,以此类推。